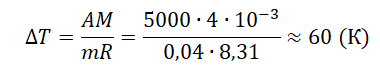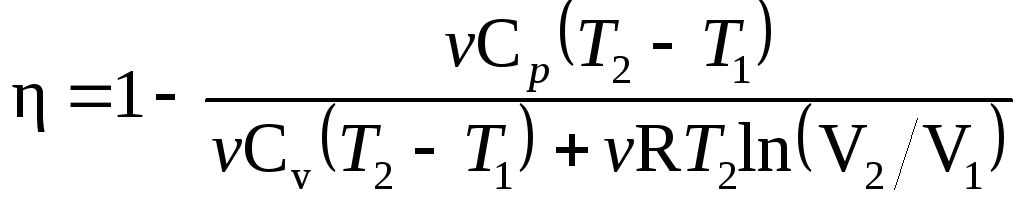Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.
Первое начало термодинамики
Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.
±ΔU=±Q±A‘
Пояснение:
- +∆U — внутренняя энергия газа увеличивается.
- –∆U — внутренняя энергия газа уменьшается.
- +Q — газ нагревают (газу передают количество теплоты).
- –Q — газ охлаждается (газ отдает тепло окружающей среде).
- +A’ — газ сжимает внешняя сила.
- –A’ — газ расширяется, совершая работу.
Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.
Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?
Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:
Q = A – U = 500 – 300 = 200 (Дж)
Зависимость физических величин
Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:
ΔU=32νRΔT
Работа идеального газа зависит от изменения его объема:
A‘=pΔV
Первое начало термодинамики для изопроцессов
| Изотермический процесс (T = const) |
ΔU=0, Q=A‘ |
| Изохорный процесс (V = const) |
A‘=0, ΔU=Q |
| Изобарное расширение газа (p = const) |
ΔU=Q−pΔV ΔU=Q−νRΔT |
| Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0) |
Q=0, ΔU=A‘ |
Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?
18 кДж = 18000 Дж
Внутреннюю энергию газа можно определить по формуле:
ΔU=32νRΔT
Отсюда изменение температуры равно:
ΔT=2ΔU3νR
Уравнение состояния идеального газа для 1 и 2 состояния:
p1V=νRT1
p2V=νRT2
Отсюда давления равны:
p1=νRT1V
p2=νRT2V
Разность давлений:
p2−p1=νRT2V−νRT1V=νRVΔT=νRV·2ΔU3νR=2ΔU3V
p2−p1=2·180003·0,6=20000 (Па)=20 (кПа)
Графические задачи на первое начало термодинамики
Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.
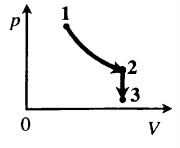
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?
Порядок решения:
1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.
T1 = T2 = 300 К; T3 = 100 К
2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.
Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.
3. Записать для него первое начало термодинамики.
В данном процессе:
ΔU=Q
4. Учитывая характер изменения величин, правильно расставить знаки: −ΔU=−Q.
5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.
Формула изменения внутренней энергии газа:
ΔU=32νRΔT
Формула работы газа:
A‘=pΔV
Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:
Изменение внутренней энергии равно:
Q23=32νRΔT23=32·1·8,31·200=2493 (Дж)
Задание EF17492
- A
- B
- C
- D
Алгоритм решения
- Определить тип теплопередачи.
- Вспомнить, как происходит этот тип теплопередачи.
- Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.
Решение
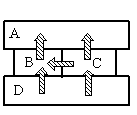
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.
На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 оС.
Ответ: A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17562
Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?
Ответ:
а) увеличилась на 300 Дж
б) уменьшилась на 300 Дж
в) увеличилась на 600 Дж
г) уменьшилась на 600 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 300 Дж.
Первое начало термодинамики:
ΔU=Q+A
Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:
ΔU=Q=300 (Дж)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17597
Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на
Ответ:
а) 5 кДж
б) 10 кДж
в) 15 кДж
г) 25 кДж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 10 кДж.
• Работа, совершенная газом: A = 15 кДж.
Первое начало термодинамики:
ΔU=Q+A
В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:
ΔU=Q−A=10−15=−5 (кДж)
Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17579
При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?
Ответ:
а) 60 К
б) 25 К
в) 15 К
г) 3 К
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать первое начало термодинамики.
3.Записать формулу для расчета работы газа.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и выполнить вычисления искомой величины.
Решение
Запишем исходные данные:
• Газ совершил работу: A = 5 кДж.
• Масса гелия: m = 0,04 кг.
5 кДж = 5000 Дж
Первое начало термодинамики:
ΔU=Q+A
Учтем, что не над газом совершают работу, а сам газ совершает ее:
Отсюда:
ΔU=Q−A
Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.
Работа, совершенная газом, равна:
A=pΔV=mMRΔT
Молярная масса гелия равна 4∙10–3 кг/моль.
Отсюда:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.9k
На чтение 7 мин. Опубликовано 14.03.2023
Содержание
- Первый закон термодинамики.
- Применение первого закона термодинамики к различным процессам .
- Изохорный процесс.
- Количество теплоты отданное газом в окружающую среду
Первый закон термодинамики.
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Манером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
где ΔU — изменение внутренней энергии, A — работа внешних сил, Q — количество теплоты, переданной системе.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение (ΔU = A + Q) записывается в виде:

где A’ — работа, совершаемая системой (A’ = -A).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника (т. е. только за счет внутренней энергии).
Действительно, если к телу не поступает теплота (Q — 0), то работа A’, согласно уравнению 
Следует помнить, что как работа, так и количество теплоты, являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам .
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс.
Зависимость р(Т) на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинамический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется (ΔV= 0), и, согласно первому началу термодинамики 
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа (А = рΔV=0) газом не совершается.
Источник
Количество теплоты отданное газом в окружающую среду
В медный калориметр массой 500 г, находившийся при температуре 20 °C, налили 200 г воды, температура которой была равна 50 °C. Через некоторое время, когда между водой и калориметром установилось тепловое равновесие, температура воды в нём оказалась равной 40 °C. Какое количество теплоты было отдано водой и калориметром в окружающую среду?
Теплота, полученная калориметром, равна
Теплота, отданная водой, равна
Теплота, отданная в окружающую среду, равна
В алюминиевый калориметр массой 300 г, находившийся при температуре 20 °C, налили 200 г воды, температура которой была равна 50 °C. Через некоторое время, когда между водой и калориметром установилось тепловое равновесие, температура воды в нём оказалась равной 40 °C. Какое количество теплоты было отдано водой и калориметром в окружающую среду?
Теплота, полученная калориметром, равна
Теплота, отданная водой, равна
Теплота, отданная в окружающую среду, равна
Аналоги к заданию № 25242: 25279 Все
Твёрдое тело остывает. На рисунке представлен график зависимости температуры тела от отданного им количества теплоты. Удельная теплоёмкость тела 500 Дж/(кгК). Чему равна масса тела? (Ответ дать в килограммах.)
Отданное количество теплоты равно Q определяется как произведение массы тела, удельной теплоемкости вещества и приращения температур: При остывании тела на 60 K было отдано 60 кДж, следовательно, масса тела
Согласно предположению И. Ньютона, которое он проверил экспериментально, тепловая мощность, отдаваемая нагретым до температуры Т телом в окружающую среду с более низкой температурой Т0, пропорциональна разности температур тела и среды. Отсюда следует, что скорость охлаждения тела Это уравнение можно решать численно, действуя следующим образом. Разобьём время охлаждения тела на одинаковые интервалы
в течение каждого из которых будем считать разность температур Ti−T0 постоянной. Затем найдём величину
— это изменение температуры тела за интервал времени
Продолжая такую процедуру, можно определить ход зависимости T(t).
Пусть старинный чугунный утюг массой m = 1,8 кг остывает от 200 °С до 100 °С в воздухе с температурой Т0 = 20 °С. Выберем = 3 мин. Удельная теплоёмкость чугуна c = 500
, коэффициент k = 0,05 мин −1 . Рассчитайте, чему будет равна температура утюга через 3 мин, 6 мин, 9 мин и т. д. с момента начала остывания до момента достижения конечной температуры.
1) Постройте по найденным точкам график зависимости температуры T утюга от времени t.
2) За какое время t0 утюг остынет от 200 °С до 100 °С?
3) Чему равна средняя мощность теплоотдачи утюга во внешнюю среду за время остывания t0? Поясните ответы на эти вопросы, указав, какие физические явления и закономерности Вы использовали при решении задачи.
1. Согласно условию задачи, в течение первых трёх минут остывания разность температур утюга и воздуха можно считать равной Tн − T0 = 200 °C − 20 °C = 180 °C, так что а температура утюга в конце первого интервала равна
В течение второго интервала остывания разность температур утюга и воздуха можно считать равной
так что
а температура утюга в конце первого интервала равна
2. Продолжим расчёт, занося результаты в таблицу и округляя температуры до десятых долей °C:
| i | |
|||
|---|---|---|---|---|
| 1 | 180,0 | 27,0 | 173,0 | 3 |
| 2 | 153,0 | 23,0 | 150,0 | 6 |
| 3 | 130,0 | 19,5 | 130,5 | 9 |
| 4 | 110,5 | 16,5 | 114,0 | 12 |
| 5 | 94,0 | 14,0 | 100,0 | 15 |
3. Строим график T(t). Таким образом, утюг остыл от 200 °C до 100 °C за 5 интервалов, т. е. за t0 = 15 минут. При этом утюг отдал воздуху количество теплоты а средняя мощность теплоотдачи составила
Согласно предположению И. Ньютона, которое он проверил экспериментально, тепловая мощность, отдаваемая нагретым до температуры Т телом в окружающую среду с более низкой температурой Т0, пропорциональна разности температур тела и среды. Отсюда следует, что скорость охлаждения тела Это уравнение можно решать численно, действуя следующим образом. Разобьём время охлаждения тела на одинаковые интервалы
в течение каждого из которых будем считать разность температур Ti−T0 постоянной. Затем найдём величину
— это изменение температуры тела за интервал времени
Продолжая такую процедуру, можно определить ход зависимости T(t).
Пусть стальной чайник с кипятком общей массой m = 3 кг остывает от 100 °С до примерно 40 °С в воздухе с температурой Т0 = 20 °С. Выберем = 4 мин. Удельная теплоёмкость чайника вместе с водой равна c = 3000 Дж/
коэффициент k = 0,05 мин −1 . Рассчитайте, чему будет равна температура чайника через 4 мин, 8 мин, 12 мин и т. д. с момента начала остывания до момента достижения конечной температуры.
1) Постройте по найденным точкам график зависимости температуры T чайника от времени t.
2) За какое время t0 чайник остынет от 100 °С до примерно 40 °С?
3) Чему равна средняя мощность теплоотдачи чайника во внешнюю среду за время остывания t0? Поясните ответы на эти вопросы, указав, какие физические явления и закономерности Вы использовали при решении задачи.
1. Согласно условию задачи, в течение первых четырёх минут остывания разность температур утюга и воздуха можно считать равной Tн − T0 = 100 °C − 20 °C = 80 °C, так что а температура утюга в конце первого интервала равна
В течение второго интервала остывания разность температур утюга и воздуха можно считать равной
так что
а температура утюга в конце первого интервала равна
2. Продолжим расчёт, занося результаты в таблицу и округляя температуры до десятых долей °C:
| i | |
|||
|---|---|---|---|---|
| 1 | 80,0 | 16,0 | 84,0 | 4 |
| 2 | 64,0 | 12,8 | 71,2 | 8 |
| 3 | 51,2 | 10,2 | 61,0 | 12 |
| 4 | 41,0 | 8,2 | 52,8 | 16 |
| 5 | 32,8 | 6,6 | 46,2 | 20 |
3. Строим график T(t). Таким образом, утюг остыл от 100 °C до примерно 40 °C за 6 интервалов, т. е. за t0 = 24 минуты. При этом утюг отдал воздуху количество теплоты а средняя мощность теплоотдачи составила
Источник
Связь между
молярной (Cm)
и удельной (с) теплоемкостями газа
Cm=cM,
где М
— молярная
масса газа.
Молярные
теплоемкости*
при
постоянном объеме и постоянном давлении
соответственно равны
Cv=iR/2;
Cp=(i+2)R/2
где i
— число
степеней свободы; R
— молярная
газовая постоянная.
Удельные
теплоемкости при постоянной объеме и
постоянном давлении соответственно
равны
,
.
Уравнение Майера
Cр—Сv=R.
Показатель
адиабаты
,
или
,
или.
Внутренняя
энергия идеального газа
U=N<>
или U=vCvT,
где <>—средняя
кинетическая энергия молекулы;
N—число
молекул газа;
v
— количество
вещества.
Работа, связанная
с изменением объема газа, в общем случае
вычисляется по формуле
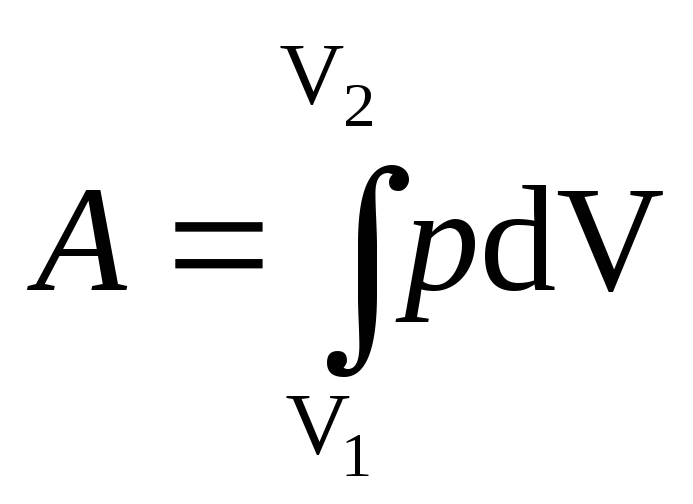
где V1
— начальный
объем газа; V2
— его
конечный объем.
Работа газа:
а) при изобарном
процессе (p=const)
A=p(V2
—
V1);
б) при изотермическом
процессе (T=const)
;
*
Здесь и далее
в целях упрощения записи в индексах
обозначений молярной теплоемкости при
постоянном давлении и постоянном объеме
букву «m»
будем опускать.
в) при адиабатном
процессе
,
или
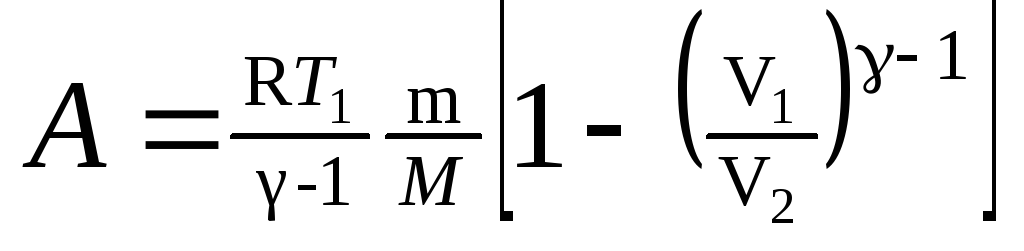
где T1
— начальная
температура газа; T2
— его
конечная температура.
Уравнение Пуассона
(уравнение газового состояния при
адиабатном процессе)
.
Связь между
начальным и конечным значениями
параметров состояний газа при адиабатном
процессе:
.
Первое начало
термодинамики в общем случае записывается
в виде
Q=U+A,
где Q
– количество теплоты, сообщённое газу;
U—изменение
его внутренней энергии; А
—
работа, совершаемая газом против внешних
сил.
Первое начало
термодинамики:
а) при изобарном
процессе
б) при изохорном
процессе (A=0)
;
в) при изотермическом
процессе (U=0)
,
г) при адиабатном
процессе (Q=0)
.
Термический
коэффициент полезного действия (КПД)
цикла
в
общем случае
,
где Q1—количество
теплоты, полученное рабочим телом
(газом) от нагревателя; Q2—количество
теплоты, переданное рабочим телом
охладителю.
КПД цикла Карно
,
или
,
где T1
— температура
нагревателя; T2
— температура
охладителя.
Изменение энтропии
где A
и B
— пределы
интегрирования, соответствующие
начальному и конечному состояниям
системы. Так как процесс равновесный,
то
интегрирование проводится по любому
пути.
Формула Больцмана
S=klnW,
где
S — энтропия
системы;
W
—
термодинамическая вероятность ее
состояния; k
—
постоянная Больцмана.
Примеры решения задач
Пример
1. Вычислить
удельные теплоемкости неона и водорода
при постоянных объеме (сv)
и давлении (cp),
принимая эти газы за идеальные.
Решение.
Удельные теплоемкости идеальных газов
выражаются формулами
; (1)
. (2)
Для неона (одноатомный
газ) i1=3,
M1=2010-з
кг/моль.
Подставив в формулы
(1) и
(2) значения
i1,
M1
и R
и произведя вычисления, найдем:
сv1=
624
Дж/(кгК);
сp1=1,04
кДж/(кгК).
Для водорода
(двухатомный газ) i2=5,
M2=210-3
кг/моль.
Вычисление по
формулам
(1) и
(2) дает
следующие значения удельных теплоемкостей
водорода:
сv2=10,4
кДж/(кгK);
сp2=14,6
кДж/(кгK).
Пример
2. Вычислить
удельные теплоемкости сv
и сp
смеси неона и водорода. Массовые доли
газов соответственно равны 1=0,8
и 2=0,2.
Значения удельных теплоемкостей газов
взять из примера
1.
Решение.
Удельную теплоемкость смеси при
постоянном объеме сv
найдем из следующих рассуждений. Теплоту,
необходимую для нагревания смеси на
T,
выразим двумя соотношениями:
Q=сv(m1+m2)T
(1)
где сv
— удельная
теплоемкость смеси; m1
— масса
неона; m2
— масса
водорода, и
Q=(сv1m1+
сv2m2)T (2)
где сv1
и сv2
— удельные
теплоемкости неона и водорода
соответственно.
Приравняв правые
части выражений
(1) и
(2) и разделив
обе части полученного равенства на
T,
найдем
сv(m1+m2)=
сv1m1+
сv2m2,
откуда
Отношения
1=m1/(m1+m2)
и 1=m2/(m1+m2)
выражают массовые доли соответственно
неона и водорода. С учетом этих обозначений
последняя формула, примет вид
сv=сv11+
сv22.
Подставив в эту
формулу числовые значения величин,
найдем
сv=2,58
кДж/(кгК).
Рассуждая
таким
же
образок, получим формулу для вычисления
удельной теплоёмкости смеси при
постоянном давлении:
cp=сp11+
сp22
Произведя вычисления
по этой формуле, найдем
cp=3,73
кДж/(кгК).
Пример
3. Определить
количество теплоты, поглощаемой
водородом массой m=0,2
кг при нагревании его от температуры
t1=0°С
до температуры t2=100
°С при постоянном давлении. Найти также
изменение внутренней энергии газа и
совершаемую им работу.
Решение.
Количество теплоты Q,
поглощаемое газом при изобарном
нагревании, определяется по формуле
Q=mcpT,
(1)
где m
— масса
нагреваемого газа; cp
— его
удельная теплоемкость при постоянном
давлении; T
— изменение температуры газа.
Как известно,
.
Подставив это выражение cp
в формулу
(1), получим
Произведя вычисления
по этой формуле, найдем
Q=291
кДж.
Внутренняя энергия
выражается формулой
,
следовательно, изменение внутренней
энергии
.
После подстановки
в эту формулу числовых значений величин
и вычислений получим U=208
кДж.
Работу расширения газа
определим по формуле, выражающей первое
начало термодинамики: Q=U+A,
откуда
A=Q — U.
Подставив значения
Q и U,
найдем
А
=83 кДж.
Пример
4. Кислород
занимает объем V1=1
м3
и находится под давлением р1=200
кПа. Газ нагрели сначала при постоянном
давлении до объема V2=3
м2,
a
затем при постоянном объеме до давления
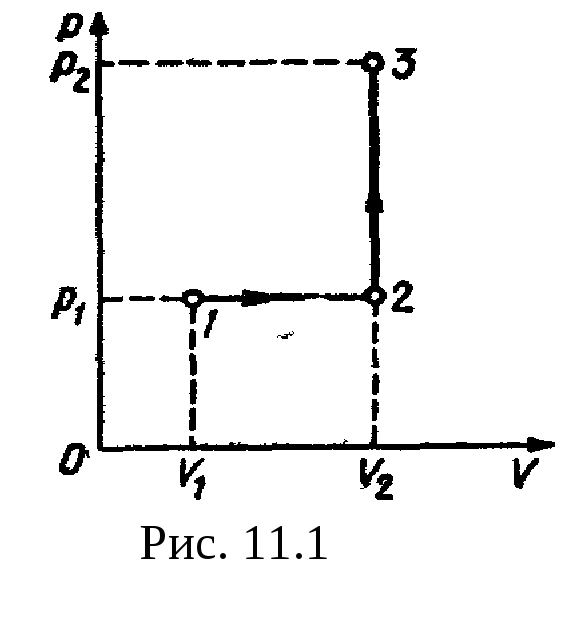
Рис
11.1 р2=500
кПа. Построить график процесса и найти:
1) изменение
U
внутренней энергии газа; 2)
совершенную им работу A;
3) количество
теплоты
Q,
переданное
газу.
Решение.
Построим график процесса (рис.
11.1). На
графике точками
1, 2, 3
обозначены состояния газа, характеризуемые
параметрами (р1,
V1,
T1),
(р1,
V2,
T2),
(р2,
V2,
T3).
1.
Изменение внутренней энергии газа при
переходе его из состояния
1 в состояние
3 выражается
формулой
U=cvmT,
где cv
— удельная
теплоемкость газа при постоянном объеме;
m
— масса
газа; T
— разность
температур, соответствующих конечному
3 и
начальному 1 состояниям, т. е. T=T3—
T1.
Так как
;
где М
— молярная
масса газа, то
.
(1)
Температуры T1
и T3
выразим из уравнения Менделеева
— Клапейрона
():
С учетом этого
равенство
(1) перепишем
в виде
U=(i/2)(p2V2—p1V1).
Подставим сюда
значения величин (учтем, что для кислорода,
как двухатомного газа, i=5)
и произведем вычисления:
U=3,25
МДж.
2.
Полная работа, совершаемая газом, равна
A=A1+A2,
где A1
— работа
на участке
1—2; A2
— работа
на участке
2—3,
На участке
1—2 давление
постоянно (p=const).
Работа в этом случае выражается формулой
A1=p1V=p1(V2—V1).
На участке 2—3
объем газа не изменяется и, следовательно,
работа газа на этом участке равна нулю
(A2=0).
Таким образом,
A=A1=p1(V2—V1).
Подставив в эту
формулу значения физических величин,
произведем вычисления:
A=0,4
МДж
3.
Согласно первому началу термодинамики,
количество теплоты Q,
переданное газу, равно сумме работы
A,
совершенной газом, и изменению U
внутренней энергии:
Q=A+U,
или
Q=3,65 МДж.
Пример
5. Идеальный
двухатомный газ, содержащий количество
вещества v=l
моль, находится под давлением p1=250кПа
и занимает объем V1==10
л. Сначала газ изохорно нагревают до
температуры T2=400
К. Далее, изотермически расширяя, доводят
его до первоначального давления.
После этого путем изобарного сжатия
возвращают газ в начальное состояние.
Определить термический КПД
цикла.
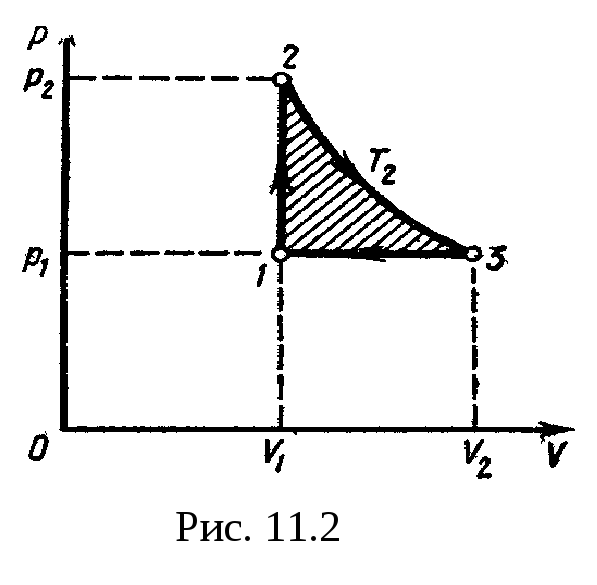
Решение.
Для наглядности построим сначала график
цикла, который состоит из изохоры,
изотермы и изобары. В координатах р,
Vэтот
цикл имеет вид. представленный на рис.
11.2. Характерные
точки цикла обозначим
1, 2, 3.
Термический КПД
любого цикла определяется выражением
=(Q1
– Q2)/Q1,
или =l
– Q2/Q1,
(1) где
Q1
—
количество теплоты, полученное газом
за цикл от нагревателя; Q2
— количество теплоты, отданное газом
за цикл охладителю.
Заметим, что разность
количеств теплоты Q1
– Q2
равна работе A,
совершаемой газом за цикл.
Эта
работа на графике в координатах р,
V (рис.
11.2)
изображается площадью цикла (площадь
цикла заштрихована).
Рабочее вещество
(газ) получает количество теплоты
Q1
на двух участках: Q1-2
на участке
1—2 (изохорный
процесс) и Q2-3
на участке
2—3
(изотермический процесс). Таким образом,
Q1=Q1-2+Q2-3.
Количество теплоты,
полученное газом при изохорном процессе,
равно
Q1-2=Cvv(T2
–
T1),
где Cv
— молярная
теплоемкость газа при постоянном объеме;
v
— количестве вещества. Температуру T1
начального состояния газа найдем,
воспользовавшись уравнением Клапейрона
— Менделеева:
T1=p1V1/(vR).
Подставив числовые
значения и произведя вычисления, получим
Количество теплоты,
полученное газом при изотермическом
процессе, равно
Q2-3=vRT2ln(V2/V1),
где V2
—
объем, занимаемый газом при температуре
T2
и давлении p1
(точка
3 на графике).
На участке
3—1 газ
отдает количество теплоты Q2,
равное
Q2=Q3-1=Cpv(T2
–T1),
где Cp
— молярная
теплоемкость газа при изобарном процессе.
Подставим найденные
значения
Q1
и Q2
в формулу
(1):
В полученном
выражении заменим отношение объемов
V2/V1,
согласно закону Гей-Люссака, отношением
температур (V2/V1=T2/T1)
и выразим Cv
и Cp
через число степеней свободы молекулы
[Cv=iR/2,
Cp=(i+2)R/2].
Тогда после сокращения на
v
и R/2
получим
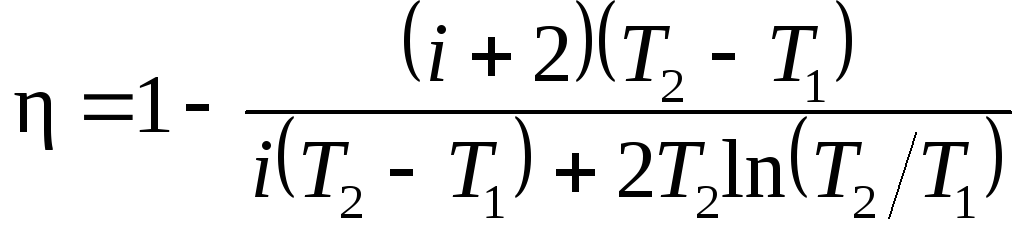
Подставив значения
i,
T1,
T2
и R
и произведя вычисления, найдем
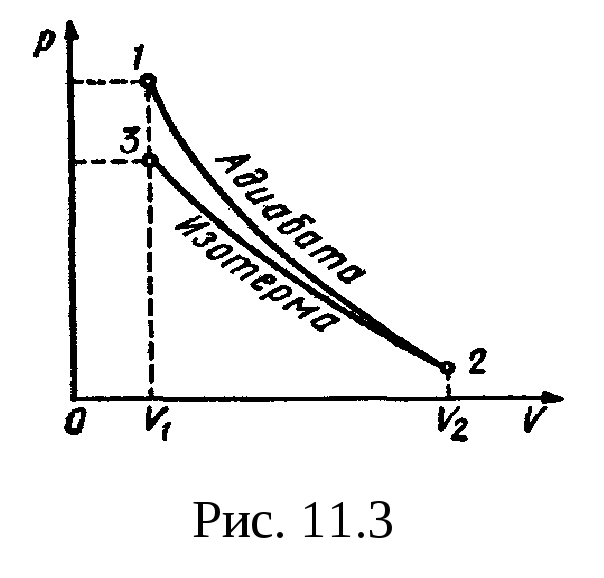
Пример 6.
В цилиндре под поршнем находится водород
массой m=0,02
кг при температуре T1=300K.
Водород начал расширяться адиабатно,
увеличив свой объем в пять раз, а затем
был сжат изотермически, причем объем
газа уменьшился в пять раз. Найти
температуру Т2,
в конце адиабатного расширения и работу
А,
совершенную газом. Изобразить процесс
графически.
Решение.
Температуры и объемы газа, совершающего
адиабатный процесс, связаны между
собой соотношением
,
где —
показатель адиабаты (для водорода как
двухатомного газа =1,4).
Отсюда получаем
выражение для конечной температуры T2:
.
Подставляя числовые
значения заданных величин, находим
.
Прологарифмируем
обе части полученного выражения:
lgT2=lg300+0,4(lgl
— lg5)=2,477+0,4( -0,699)=2,477—0,280=2,197.
Зная lgT2,
по таблицам антилогарифмов находим
искомое значение T2:
T2=157
К.
Работа A1
газа при адиабатном расширении
определяется по формуле
.
Подставив сюда
числовые значения величин, после
вычисления получим
Работа A2
газа при изотермическом сжатии выражается
формулой
A2=RT2(m/M)ln(V2/V1).
Произведя вычисления
по этой формуле, найдем
A2=
-21 кДж.
Знак минус показывает,
что при сжатии газа работа совершена
внешними силами.
Общая работа,
совершенная газом при рассмотренных
процессах, А=A1+A2=29,8кДж
+ (-21 кДж)=8,8 кДж.
График процесса
приведен на рис.
11.3.
Пример
7. Нагреватель
тепловой машины, работающей по обратимому
циклу Карно, имеет температуру
t1==200°С.
Определить температуру Т2,
охладителя, если при получении от
нагревателя количества теплоты Q1=
1 Дж машина
совершает работу A=0,4
Дж? Потери на трение и теплоотдачу не
учитывать.
Решение.Температуру охладителя найдем, использовав
выражение для термического КПД машины,
работающей по циклу Карно,=(T1—
T2)/T1.
Отсюда
T2=
T1(1-).
(1)
Термический КПД
тепловой машины выражает отношение
количества теплоты, которое превращено
в механическою работу A,
к количеству теплоты Q1,
которое получено рабочим телом тепловой
машины из внешней среды (от нагревателя),
т. е. =A/Q1.
Подставив это выражение в формулу
(1), найдем
T2=
T1(1-A/Q).
(2)
Учтя, что T1=473
К, после вычисления по формуле
(2) получим
T2=284
К.
Пример
8. Найти
изменение S
энтропии при нагревании воды массой
m=100
г от температуры t1=0°C
до температуры
t2=100
°С и последующем превращении воды в пар
той же температуры.
Решение.
Найдем отдельно изменение энтропии S’
при нагревании воды и изменение энтропии
S»
при превращении ее в пар. Полное изменение
энтропии выразится суммой S’
и S».
Как известно,
изменение энтропии выражается общей
формулой
(1)
При бесконечно
малом изменении dT
температуры нагреваемого тела
затрачивается количество теплоты
dQ=mcdT,
где m
— масса
тела; с
— его
удельная теплоемкость. Подставив
выражение dQ
в равенство
(1), найдем
формулу для вычисления изменения
энтропии при нагревании воды:
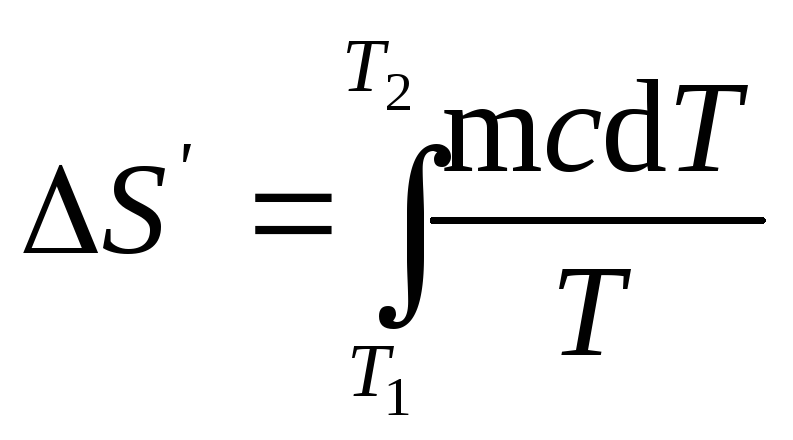
Вынесем за знак
интеграла постоянные величины и
произведем интегрирование, тогда получим
S’=mcln(T2/T1).
После вычислений
найдем S’=132
Дж/К.
При вычислении по
формуле
(1) изменения
энтропии во время превращения воды в
пар той же температуры постоянная
температуpa
T
‘выносится
за знак интеграла. Вычислив интеграл,
найдем
(2)
где Q
—
количество теплоты, переданное при
превращении нагретой воды в пар той
же температуры.
Подставив в равенство
(2) выражение
количества теплоты Q=m,
где
— удельная
теплота парообразования, получим
(3)
Произведя вычисления
по формуле
(3), найдем
S»=605
Дж/К.
Полное изменение
энтропии при нагревании воды и последующем
превращении ее в пар S=S’+S»=737
Дж/К.
Пример
9. Определить
изменение S
энтропии при изотермическом расширении
кислорода массой m=10
г от объема V1=25
л до объема V2=100
л.
Решение.
Так как процесс изотермический, то в
общем выражении энтропии
температуру выносят за знак интеграла.
Выполнив это, получим
(1)
Количество теплоты
Q, полученное
газом, найдем по первому началу
термодинамики: Q=U+A.
Для изотермического процесса U=0,
следовательно,
Q=A,
(2) а
работа А для этого процесса определяется
по формуле
A=(m/M)RT
ln(V2/V1).
(3)
С учетом
(2) и
(3) равенство
(1) примет
вид
S=(m/M)R
ln(V2/V1).
(4)
Подставив в
(4) числовые
значения и произведя вычисления, получим
S=(1010-3/(3210-3))
8,31
ln(10010-3/(2510-3))
Дж/К=3,60
Дж/К.
1. Изопроцессы и адиабатный процесс
Напомним, что согласно первому закону термодинамики количество теплоты Q, переданное газу, связано с изменением внутренней энергии газа ∆U и работой газа Aг соотношением
Q = ∆U + Aг. (1)
Часто требуется применять первый закон термодинамики к газовым процессам, представляющим собой последовательность изопроцессов (иногда добавляется еще адиабатный процесс).
Рассмотрим, как находить величины, фигурирующие в формуле (1), в этих процессах. Напомним, что каждая из тих величин может быть положительной, отрицательной или равной нулю.
Если график газового процесса задан не в координатах (p, V), то желательно начертить график этого же процесса в координатах (p, V), потому что с помощью этого графика легко найти работу газа. Напомним, что работа газа при расширении численно равна площади под графиком зависимости p(V), при сжатии газа – площади под тем же графиком, но взятой о знаком минус.
В большинстве задач на эту тему рассматривается однотомный идеальный газ. Напомним, что его внутренняя энергия выражается формулой
U = (3/2)νRT, (2)
где ν – количество вещества (число молей), R – универсальная газовая постоянная, T – абсолютная температура.
? 1. Чему равно изменение внутренней энергии газа в изотермическом процессе?
Из формулы (2) и уравнения состояния идеального газа
pV = νRT (3)
следует, что внутреннюю энергию одноатомного идеального газа можно выразить также формулой
U = (3/2)pV. (4)
С помощью этой формулы можно находить изменение внутренней энергии одноатомного идеального газа, если известны начальные и конечные значения давления и объема газа.
Например, если начальные значения давления и объема обозначить p1 и V1, а конечные – p2 и V2, то
∆U = (3/2) (p2V2 – p1V1). (5)
? 2. Чему равно изменение внутренней энергии при изохорном процессе, если объем газа равен V, а давление изменилось от p1 до p2?
? 3. Чему равно изменение внутренней энергии при изобарном процессе, если давление газа равно p, а объем изменился от V1 до V2?
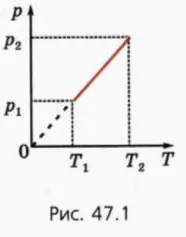
? 4. На рисунке 47.1 изображен график зависимости p(T) для ν молей одноатомного идеального газа при изохорном переходе из состояния 1 в состояние 2. Даны начальные значения давления и температуры газа p1 и T1, конечная температура T2.
а) Чему равно конечное давление газа p2?
б) Чему равен объем газа V?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии ∆U газа?
е) Чему равно полученное газом количество теплоты Q?
? 5. На рисунке 47.2 изображен график зависимости V(T), для ν молей одноатомного идеального газа при изобарном переходе из состояния 1 в состояние 2. Даны начальные значения объема и температуры газа V1, и T1, конечная температура T2.
47.2
а) Чему равен конечный объем газа V2?
б) Чему равно давление газа p?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии газа?
е) Чему равно полученное газом количество теплоты Q?
? 6. Используя результаты предыдущих заданий, сравните значения количества теплоты, полученного одним и тем же количеством вещества газа в изохорном и изобарном процессе при нагревании от температуры T1 до температуры T2.
а) В каком случае количество теплоты больше? Во сколько раз больше?
б) Объясните этот результат, используя закон сохранения энергии.
Рассмотрим теперь изотермический и адиабатный процессы.
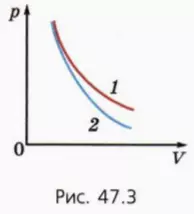
? 7. На рисунке 47.3 приведены графики зависимости p(V) для данной массы газа при изотермическом и адиабатном процессах. Какой график описывает адиабатный процесс? Поясните свой ответ.
? 8. В каком случае совершенная газом работа больше: когда он расширяется изотермически или адиабатно? Начальные объемы газа одинаковы, конечные объемы тоже одинаковы. Поясните свой ответ.
? 9. Как связаны полученное газом количество теплоты Q и работа газа Aг при изотермическом процессе?
Нахождение работы газа при изотермическом расширении выходит за рамки школьного курса физики. Но в задачах часто используется связь между Q и Aг в изотермическом процессе, выведенная вами при выполнении предыдущего задания.
? 10. В вертикальном цилиндре под поршнем массой 1 кг находится идеальный газ. При изотермическом расширении газа поршень поднялся на 5 см. Примите, что трением между поршнем и стенкой цилиндра можно пренебречь.
а) Чему равна работа газа?
б) Чему равно переданное газу количество теплоты?
? 11. Как связаны работа газа Aг и изменение его внутренней энергии ∆U при адиабатном процессе? (Напомним, что при адиабатном процессе отсутствует теплопередача, то есть Q = 0.)
Нахождение работы газа при адиабатном процессе также выходит за рамки школьного курса, но связь между Aг и ∆U в этом процессе широко используется при решении задач.
? 12. При адиабатном расширении 2 молей одноатомного идеального газа газ совершил работу 100 Дж.
а) Как изменилась при этом внутренняя энергия газа?
б) Как изменилась температура газа?
2. Циклические процессы
Циклические газовые процессы состоят из нескольких этапов, причем конечное состояние газа совпадает с начальным. Обычно рассматриваются случаи, когда этапами циклического процесса являются изопроцессы и адиабатный процесс.
Вопросы при этом ставятся, например, такие.
- На каких этапах процесса газ получает тепло, а на каких – отдает?
- Чему равно полученное газом или отданное им количество теплоты?
- Чему равно изменение внутренней энергии газа на различных этапах процесса?
- Чему равна работа газа за один цикл?
- Чему равен КПД цикла?
Для простейшего циклического процесса, состоящего из двух изохор и двух изобар, мы уже нашли ответы на эти вопросы (см. § 43). Рассмотрим теперь более сложный цикл.
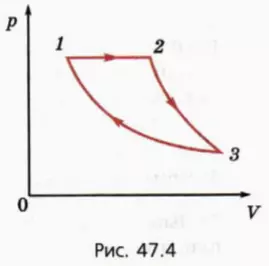
На рисунке 47.4 изображен график циклического процесса, происходящего с некоторой массой одноатомного идеального газа.
На этапе 2–3 газ адиабатно расширяется, а на этапе 3–1 изотермически сжимается.
Известно, что при изобарном расширении газ совершает работу A, а при изотермическом сжатии отдает холодильнику количество теплоты Qхол. Требуется найти КПД цикла.
Проанализируем сначала этот циклический процесс качественно. По определению КПД цикла равен отношению работы, совершенной газом за один цикл, к количеству теплоты, переданному газу за этот цикл.
Работа, совершенная газом за один цикл, равна разности работы, совершенной газом при его расширении, и работы, совершенной над газом при его сжатии.
? 13. На каких этапах процесса газ совершает работу, а на каких этапах работу совершают над газом?
? 14. На каких этапах процесса газ получает тепло?
Перейдем теперь к количественному описанию. Заметим, то в подобных задачах как работу газа, так и количество теплоты удобно выражать через число молей газа и значения абсолютной температуры газа в различных состояниях газа, даже если эти значения не заданы (в таком случае они сократятся, если найдено правильное решение).
Обозначим T1, T2 и T3 значения абсолютной температуры соответственно в состояниях 1, 2, 3. Поскольку процесс 3–1 изотермический, T1 = T3.
? 15. Рассмотрим сначала изобарный процесс 1–2.
а) Выразите работу газа через давление p в этом процессе и значения объемов газа в состояниях 1 и 2.
б) Выразите эту работу через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
в) Выразите изменение внутренней энергии газа в процессе 1–2 через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
г) Выразите количество теплоты, полученное газом в процессе 1–2, через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
д) Как связано переданное газу количество теплоты с работой, совершенной газом?
? 16. Рассмотрим адиабатный процесс 2–3.
а) Каково соотношение между работой газа в этом процессе и изменением его внутренней энергии?
б) Выразите работу газа в этом процессе через число молей газа и значения абсолютной температуры в состояниях 2 и 3.
в) Найдите соотношение между работой газа в процессе 1–3 и работой газа в процессе 2–3.
? 17. Рассмотрим изотермический процесс 3–1.
а) Найдите соотношение между работой газа в этом процессе и количеством теплоты, полученным газом. Учтите, что в данном случае обе эти величины отрицательны.
б) Выразите работу Aвнеш, совершенную в этом процессе над газом, через количество теплоты Qхол, отданное газом холодильнику.
Используя результаты, полученные при выполнении предыдущих заданий, получаем, что работу Aц, совершенную газом за дин цикл, можно выразить через заданные величины:
3. Расширение газа под поршнем
Трением между поршнем и стенкой сосуда можно пренебречь
Если цилиндрический сосуд с газом расположен вертикально и трением между поршнем и стенками сосуда можно пренебречь, то при медленном нагревании процесс является изобарным. Работа газа
Aг = mgh,
где m – масса поршня, h – расстояние, на которое поднялся поршень. Используя первый закон термодинамики
Q = ∆U + Aг,
можно связать перемещение поршня с переданным газу количеством теплоты Q и изменением его внутренней энергии ∆U. Ее можно выразить через изменение температуры ∆T и число молей газа.
? 18. Одноатомный идеальный газ находится в вертикальном цилиндрическом сосуде под поршнем массой 2 кг. Когда газу передали количество теплоты, равное 10 Дж, поршень поднялся на 5 см, а температура газа увеличилась на 2 К. Трением между поршнем и стенкой сосуда можно пренебречь. Сколько молей газа содержится в сосуде?
Учет трение между поршнем и стенкой сосуда
Типичная ошибка при решении подобных задач состоит в ом, что не учитывают силу трения покоя. Дело в том, что при увеличении давления газа под поршнем он не сдвинется с места до тех пор, пока равнодействующая приложенных к нему сил не превысит максимальную силу трения покоя, которую обычно принимают равной силе трения скольжения. Только поле этого поршень начнет двигаться, и газ начнет расширяться.
Рассмотрим пример. Пусть теперь сосуд расположен горизонтально: в таком случае вес поршня не играет роли.
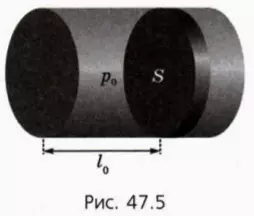
? 19. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Начальное давление газа равно p0, начальное расстояние от дна сосуда до поршня равно l0, площадь поршня S (рис. 47.5).
При движении поршня на него со стороны стенки сосуда действует сила трения скольжения Fтр. Будем считать, что сосуд находится в вакууме (то есть на поршень не действует сила атмосферного давления). В начальный момент поршень находится в равновесии. Газу передают некоторое количество теплоты.
а) Какое соотношение между p0, Fтр и S следует из условия, что в начальный момент поршень находится в равновесии?
б) При каком давлении p газа поршень начнет двигаться?
в) Насколько должна увеличиться внутренняя энергия газа, чтобы поршень начал двигаться?
г) Какое количество теплоты Q надо сообщить газу, чтобы поршень начал двигаться?
д) Чему будет равно давление p газа, когда поршень будет двигаться равномерно?
е) Какую работу A совершит газ при равномерном перемещении поршня на расстояние d?
ж) Насколько увеличится при этом внутренняя энергия газа по сравнению с ее начальным значением?
з) Какое количество теплоты Q надо передать газу в начальном состоянии, чтобы поршень сдвинулся на расстояние d?
Дополнительные вопросы и задания
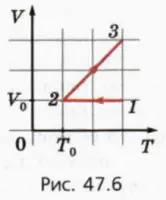
20. На рисунке 47.6 изображен процесс, происходящий с ν молями одноатомного идеального газа.
а) Начертите график этого процесса в координатах (p, V).
б) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 1–2? Учтите, что эти значения могут быть отрицательными.
в) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 2–3?
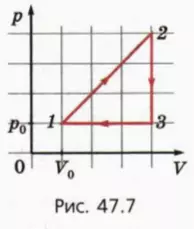
21. На рисунке 47.7 изображен график цикла, происходящего с одноатомным идеальным газом. Найдите КПД цикла.
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023