поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
Дано
с= 4200 Дж/кг*С -вода -удельная теплоемкость
T1=100 C
T2=50 C
p=1000кг/м3 -плотность воды
m=3кг
—————————
Q -?
РЕШЕНИЕ
ВОДА/КИПЯТОК отдает тепло Q -отрицательне значение
Q=cm(T2-Т1) =4200*3*(50-100)= -630000 Дж=-630 кДж=-0.630 МДж
Ответ 630000 Дж=630 кДж=0.630 МДж любой ответ
ДОМАШНЯЯ ПРАКТИЧЕСКАЯ РАБОТА
«ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ТЕПЛОТЫ, ОТДАВАЕМОГО ОРГАНИЗМОМ ЧЕЛОВЕКА В ОКРУЖАЮЩУЮ СРЕДУ»
Цель работы: измерив термометром температуру окружающего воздуха и весами – массу своего тела, определить количество теплоты (а также количество вещества), которое отдает ваше тело в окружающее пространство.
Оборудование: термометр, напольные весы.
Ход работы:
1. Найдите массу собственного тела, используя напольные весы.
2. Измерьте температуру воздуха и температуру вашего тела.
3. Приняв молярную массу вещества человеческого тела 
4. По формуле 
Удельную теплоемкость человека (так как он состоит на 80% из воды) можно приблизительно считать равной
Результаты измерений и вычислений занесите в отчетную таблицу:
|
Молярная масса,
|
Масса человека, (кг) |
Количество вещества, (кг) |
Удельная теплоемкость человека ( |
Температура воздуха, (0С) |
Температура тела, (0С) |
Количество теплоты, отдаваемое организмом человека в окружающую среду
|
Обобщите результаты своей работы. Сделайте вывод по проделанной работ.
Решите задачи:
Для приготовления чая турист положил в котелок лед массой 2 кг, имеющий температуру 00С. Какое количество теплоты необходимо для превращения этого льда в кипяток при температуре 1000С? Энергию, израсходованную на нагревание котелка, не учитывать.
Какое количество энергии требуется для превращения воды массой 2 кг, взятой при температуре 200С, в пар?
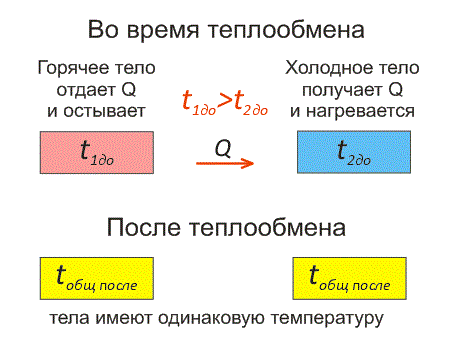
Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.