Решение
Изменение внутренней энергии в рассматриваемом процессе 
. Следовательно,


. Ответ:

Ответ

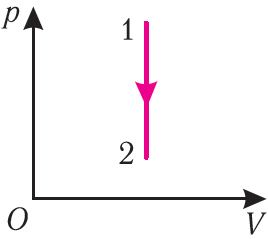
Определить количество теплоты, необходимое для перевода одного моля одноатомного идеального газа из состояния 1 в состояние 3. В состоянии 1 температура газа T1 = 300 К.
Спрятать решение
Решение.
При изобарном процессе Изменение внутренней энергии одноатомного газа
По первому закону термодинамики
При изохорном процессе Изменение внутренней энергии
Количество теплоты равно
Тогда при переходе получено количество теплоты
Из уравнения Клапейрона-Менделеева откуда количество теплоты, полученное газом, равно
Ответ: 13,7 кДж.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 10 класса, Х.: «Гимназия», 2002 (№ 1 (высок.) стр. 44)
Два
моля идеального одноатомного газа сначала расширяются изобарно, а затем
изохорно переходят в состояние с начальной температурой 300 K. Определите количество теплоты, переданной газу, если объем в
этом процессе увеличился в 6 раз.
Решение.
Согласно
первому началу термодинамики количество теплоты, сообщенное системе,
расходуется на увеличение ее внутренней энергии и на работу, совершаемую
системой против внешних сил: Q = DU + A. В частности, при изобарном расширении газа Q1 = DU1 + A1 , где изменение внутренней
энергии газа DU1.
T – температура газа
после завершения этого процесса. При изохорном процессе Q2 = DU2 + A2 = DU2.
Тогда
полное количество переданной газу теплоты Q
= Q2 + Q2 = A1 = (n-1)vRT1 = 5•2,0•8,31•300 = 25
кДж.
Ответ:
Q = 25 кДж.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 14. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам изменения состояния идеального газа |
| Напечатано:: | Гость |
| Дата: | Понедельник, 29 Май 2023, 08:20 |
Оглавление
- Закон сохранения энергии
- Первый закон термодинамики
- Изохорный процесс
- Изотермический процесс
- Изобарный процесс
- Адиабатный процесс
- Примеры решения задач
- Упражнение 10
В 9-м классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия?
Закон сохранения энергии. В середине XIX в. известный английский физик Дж. Джоуль (1818–1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814–1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX в. Г. Гельмгольца (1821–1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы.
Закон сохранения и превращения энергии: при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Закон сохранения и превращения энергии является всеобщим законом природы и связывает воедино все физические явления. Этот закон выполняется абсолютно точно, на нём базируется всё современное естествознание.
От теории к практике
Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1–2 °С. Что является причиной повышения температуры воды?
Первый закон термодинамики. В предыдущих параграфах мы рассматривали процессы, в которых внутренняя энергия системы изменялась или при совершении работы, или в результате теплообмена. Однако чаще всего при переходе системы из одного состояния в другое внутренняя энергия изменяется как за счёт совершения работы, так и за счёт теплообмена с окружающими телами.
Для термодинамических систем закон сохранения и превращения энергии называют первым законом термодинамики.
Первый закон термодинамики: приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного (или отданного) системой при взаимодействии с внешними телами.
ΔU = A′ + Q.
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (A′ = –A), то первый закон термодинамики можно сформулировать иначе:
Количество теплоты, полученное (или отданное) термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую она совершает против внешних сил:
Q = ΔU + A.
От теории к практике
Идеальный газ получил количество теплоты Q = 340 Дж. Каково приращение внутренней энергии газа, если при этом сила давления газа совершила работу А = 300 Дж?
Если термодинамическая система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом ΔU = 0 и A = Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплообмена с внешними телами, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.
Применим первый закон термодинамики к различным изопроцессам изменения состояния идеального одноатомного газа.
Рассмотрим в качестве термодинамической системы идеальный одноатомный газ, находящийся в цилиндрическом сосуде, закрытом поршнем.
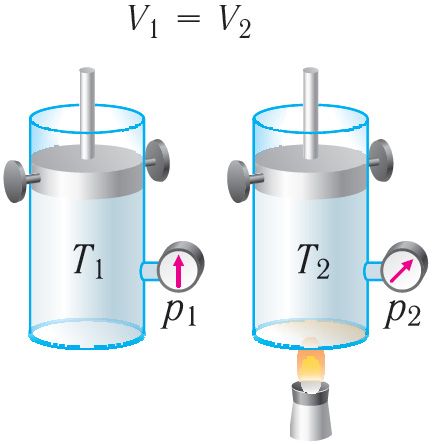
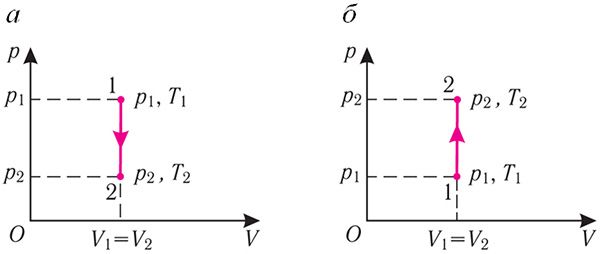
Изохорный процесс. Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем цилиндр с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 78), следовательно, работа силы давления газа A = 0. Тогда первый закон термодинамики примет вид
Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа (рис. 78.1, а). Если же газ при изохорном процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
(рис. 78.1, б).
От теории к практике
1. Каково приращение внутренней энергии идеального газа, если при изохорном процессе от него было отведено количество теплоты Q = –560 Дж?
2. Как изменяются внутренняя энергия и давление определённой массы идеального газа при изохорном повышении температуры?
Изотермический процесс. Пусть цилиндр с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. И пусть цилиндр изготовлен из вещества с хорошей теплопроводностью. В этом случае внутренняя энергия идеального одноатомного газа, находящегося в цилиндре, остаётся постоянной, и при медленном перемещении поршня её изменение ΔU = 0. Тогда первый закон термодинамики примет вид
Q = A.
Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (ΔV > 0, поскольку V2 > V1) (рис. 79), то работа силы давления расширяющегося газа A > 0 (рис. 79.1, а). При одинаковой первоначальной температуре термостата и газа теплопередача не происходит. Положительная работа силы давления расширяющегося газа совершается за счёт уменьшения его внутренней энергии, а значит, и температуры. Тут же возникает теплопередача от термостата газу. При медленном перемещении поршня в цилиндре температура газа успевает выравняться и реально происходящий процесс близок к изотермическому, при котором расширяющийся газ получает некоторое количество теплоты (Q > 0) от термостата.
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (ΔV < 0, так как V2 < V1), то работа силы давления при сжатии газа A < 0 (рис. 79.1, б) приводит к увеличению внутренней энергии, а следовательно, и его температуры. В результате возникает теплопередача от газа термостату. При сжатии газ отдаёт термостату некоторое количество теплоты Q < 0. Изотермическое сжатие газа происходит за счёт работы внешних сил: A’ > 0.
От теории к практике
1. Сила давления идеального газа при изотермическом расширении совершила работу А = 3640 Дж. Какое количество теплоты получил газ?
2. Возможно ли изотермическое сжатие (расширение) определённой массы идеального газа без теплообмена?
Изобарный процесс. Пусть газ находится в цилиндре, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 80). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики, переданное газу количество теплоты частично расходуется на увеличение внутренней энергии (ΔU > 0) системы и частично идёт на совершение работы силой давления газа при его расширении (А > 0, рис. 80.1, а): Q = ΔU + A.
При изобарном процессе работа расширения (сжатия) газа A = pΔV ≠ 0 и первый закон термодинамики принимает вид
Q = ΔU+ pΔV.
При изобарном сжатии газа внешние силы совершают работу A’ > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q < 0). Понижение температуры газа при изобарном сжатии приводит к уменьшению его внутренней энергии (ΔU < 0). Работа силы давления газа при сжатии А < 0 (рис. 80.1, б).
От теории к практике
Сила давления идеального газа при изобарном расширении совершила работу А = 320 Дж. При этом газ получил количество теплоты Q = 680 Дж. Каково приращение внутренней энергии идеального газа?
Удельная теплоёмкость вещества зависит не только от его свойств, но и от характера осуществляемого процесса теплообмена. Действительно, из формулы Q = cmΔT следует, что удельная теплоёмкость .
Тогда, согласно первому закону термодинамики, при изохорном процессе удельная теплоёмкость идеального газа , а при изобарном —
. Таким образом, для одинакового увеличения температуры при изобарном нагревании единице массы газа необходимо передать большее количество теплоты, чем при изохорном нагревании, т. е. cp > cV. Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении.
Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов, поэтому для них АΔU и их удельные теплоёмкости слабо зависят от характера осуществляемого процесса (ср ≈ сV).
Адиабатный процесс. Адиабатным называют процесс, в ходе которого термодинамическая система не получает и не отдаёт энергию путём теплообмена. Таким образом, при адиабатном процессе:
Q = 0.
Применяя к этому процессу первый закон термодинамики, получим:
ΔU = −A , или A = −ΔU.
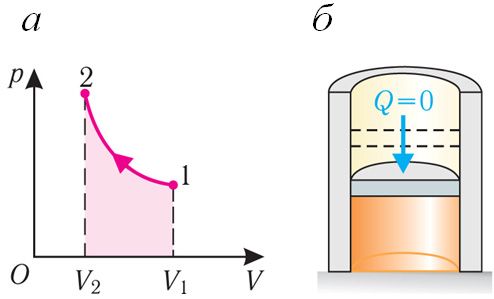
При адиабатном процессе изменение внутренней энергии системы происходит только за счёт совершения работы. Если внешние силы совершают работу по сжатию газа (ΔV < 0, А < 0) (рис. 80.2, а, б), то внутренняя энергия газа увеличивается (ΔU > 0), газ нагревается.
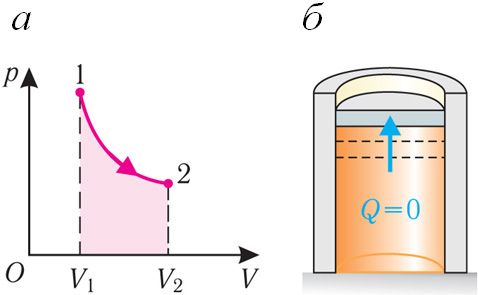
Если сила давления газа совершает работу по расширению (ΔV > 0, А > 0) (рис. 80.3, а, б), то внутренняя энергия газа уменьшается (ΔU < 0), газ охлаждается.
От теории к практике
1. При адиабатном расширении силой давления идеального газа совершена работа А = 265 Дж. Как изменилась при этом температура газа? Определите приращение внутренней энергии газа.
2. В цилиндре с подвижным поршнем находится идеальный газ, давление которого р1 и объём V1. В каком случае сила давления газа совершит большую работу: при изотермическом или адиабатном его расширении до объёма V2?
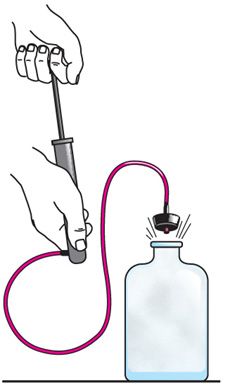
На практике адиабатный процесс осуществляют главным образом не за счёт теплоизоляции (нельзя окружить систему оболочкой, которая абсолютно не допускает теплообмена), а за счёт скорости протекания процесса. Если процесс протекает очень быстро, то теплообмен практически не проявляется. Очень нагляден опыт, иллюстрирующий уменьшение температуры газа при его адиабатном расширении. Если, используя насос, через отверстие в пробке накачивать в стеклянный сосуд воздух (рис. 80.4), то через некоторый промежуток времени сила давления сжатого воздуха совершит работу по преодолению силы трения, которой сосуд действует на пробку, и силы атмосферного давления. Теплообмен между сосудом и окружающими телами не успевает проявиться за тот малый промежуток времени, в течение которого пробка вылетает из сосуда и часть газа выходит из него. Уменьшение внутренней энергии воздуха в сосуде обусловлено не только уменьшением массы, но и понижением его температуры, что приводит к конденсации водяных паров, т. е. к образованию тумана.
Примером адиабатного процесса может служить охлаждение воздуха в атмосфере. Нагретый возле поверхности земли воздух при быстром подъёме в верхние слои атмосферы расширяется почти адиабатно и при этом существенно охлаждается. Водяной пар в нём конденсируется в маленькие капли воды и кристаллики льда, образуя облака. Процесс, близкий к адиабатному, используют в двигателях внутреннего сгорания.
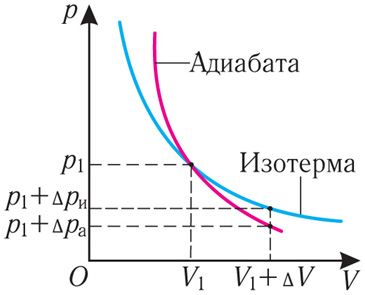
График адиабатного процесса в координатах (p, V) похож на график изотермического процесса (рис. 80.5). Однако одному и тому же изменению объёма ΔV при адиабатном процессе соответствует большее изменение давления, чем при изотермическом: . Это объясняется тем, что в случае адиабатного расширения давление p = nkT уменьшается не только за счёт увеличения объёма газа (и уменьшения концентрации частиц), но и за счёт уменьшения температуры. При изотермическом расширении давление газа уменьшается только за счёт уменьшения концентрации частиц.
1. Приведите две формулировки первого закона термодинамики.
2. Чему равно изменение внутренней энергии при изохорном процессе?
3. На что расходуется количество теплоты, сообщаемое системе при изотермическом процессе?
4. На что расходуется количество теплоты, сообщаемое системе при изобарном процессе?
5. При быстром сжатии газа произошло повышение его температуры. Означает ли это, что газу сообщили некоторое количество теплоты? Можно ли утверждать, что внутренняя энергия газа увеличилась?
6. Почему невозможно создать «вечный двигатель первого рода»?
7. Можно ли передать газу некоторое количество энергии путём теплообмена, не вызывая при этом повышения его температуры? Приведите примеры.
8. Какой процесс изменения состояния газа называют адиабатным? Как этот процесс можно осуществить?
9. В § 12 мы утверждали, что работа, совершаемая при переходе системы из одного состояния в другое, является функцией процесса, т. е. зависит не только от начального и конечного состояний, но и от вида процесса. Используя первый закон термодинамики, докажите, что количество теплоты, получаемое или отдаваемое системой при её переходе из одного состояния в другое, также является функцией процесса.
10. Заполните таблицу в тетради.
| Процесс | Работа силы давления газа | Количество теплоты | Изменение внутренней энергии | Вывод |
| Изохорный (V = const и ΔV = 0) | ||||
| Изотермический (Т = const и ΔТ = 0) | ||||
| Изобарный (р = const) | ||||
| Адиабатный (ΔU = −A) |
Примеры решения задач
Пример 1. Идеальный одноатомный газ, давление которого p = 2,0 · 105 Па, изобарно расширяется так, что его объём возрастает на ΔV = 0,40 м3. Определите приращение внутренней энергии газа и количество теплоты, получаемое им в этом процессе.
Дано:
p = 2,0 · 105 Па
ΔV = 0,40 м3
р = const
ΔU — ?
Q — ?
Решение: Приращение внутренней энергии идеального одноатомного газа При изобарном расширении идеального газа изменение его температуры
связано с изменением объёма
газа соотношением
Тогда . Согласно первому закону термодинамики для изобарного процесса
.
Следовательно, .
Ответ: ΔU = 0,12 МДж, Q = 0,20 МДж.
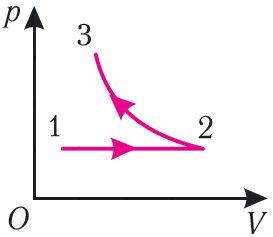
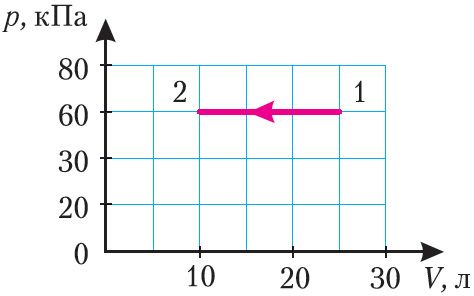
Пример 2. На рисунке 81 представлен график процесса изменения состояния некоторой массы идеального газа (участок 2 3 — изотерма). На каком участке графика работа силы давления газа: а) положительная; б) отрицательная? На каком участке графика газ: а) получал количество теплоты; б) отдавал? Как изменялась внутренняя энергия газа?
Решение. Участок 1 2. Поскольку при постоянном давлении (р = const, р1 = р2) увеличивается объём газа (ΔV12 > 0), то растёт и его температура (ΔТ12 > 0). Следовательно, работа силы давления газа А12 > 0 и приращение его внутренней энергии ΔU12 > 0. Из первого закона термодинамики, записанного в виде Q12 = ΔU12 + А12, следует, что Q12 > 0.
Участок 2 3. Поскольку температура газа не изменяется (Т = const, Т2 = Т3, ΔТ23 = 0), то приращение его внутренней энергии ΔU23 = 0. Объём газа уменьшается (изотермическое сжатие), и работа силы давления газа А23 < 0. Из первого закона термодинамики, записанного в виде Q23 = ΔU23 + А23, следует, что Q23 < 0.
Ответ:
| Участок графика | Работа силы давления газа | Количество теплоты | Приращение внутренней энергии газа |
| 1 |
А12 > 0 | Q12 > 0 (газ получал количество теплоты) | ΔU12 > 0 |
| 2 |
А23 < 0 | Q23 < 0 (газ отдавал количество теплоты) | ΔU23 = 0 |
Решение. а) Так как начальное и конечное состояния для обоих переходов одинаковы, то одинаковы и приращения внутренней энергии:
ΔU123 = ΔU143 = U3 – U1.
б) Рассмотрев рисунок, можно заключить, что площадь фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 3 и 4, меньше площади фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 1 и 2. Следовательно, в процессе перехода 12
3 сила давления газа совершает большую работу, чем в процессе перехода 1
4
3:
А123 > А143.
в) Из первого закона термодинамики следует:
Q123 = ΔU13 + А123, Q143 = ΔU13 + А143.
Поскольку приращение внутренней энергии в обоих случаях одно и то же, а совершённая силой давления газа работа больше при переходе 12
3, то количество теплоты, сообщённое газу, при переходе 1
2
3 также больше: Q123 > Q143.
Ответ: а) ΔU123 = ΔU143; б) А123 > А143; в) Q123 > Q143.
Упражнение 10
1. Определите количество теплоты, сообщённое кислороду, если при изотермическом расширении работа, совершённая силой давления газа, А = 6,4 кДж.
2. С идеальным газом определённой массы осуществлён процесс, график которого представлен на рисунке 82. Чему равна работа силы давления газа? Получал или отдавал газ количество теплоты в этом процессе? Как изменилась внутренняя энергия газа?
Заполните таблицу в тетради (см. пример 2).
| Работа силы давления газа | Количество теплоты | Приращение внутренней энергии газа |
3. С идеальным газом определённой массы осуществлён процесс, график которого представлен на рисунке 83. Определите приращение внутренней энергии газа, если он отдал количество теплоты Q12 = –2,25 кДж.
4. В герметично закрытом баллоне находится азот массой m = 4,00 кг. Определите количество теплоты, сообщённое азоту при повышении его температуры на ΔT = 120 К, если удельная теплоёмкость азота при постоянном объёме .
5. При изобарном расширении силой давления идеального одноатомного газа совершена работа А = 50,0 кДж. Определите приращение внутренней энергии газа и сообщённое ему количество теплоты.
6. Идеальный газ, количество вещества которого постоянно, испытывает адиабатное сжатие. Как изменяются в этом процессе давление и температура газа? Выберите верное утверждение.
1) Давление и температура газа уменьшаются.
2) Давление увеличивается, а температура газа уменьшается.
3) Давление уменьшается, а температура газа увеличивается.
4) Давление и температура газа увеличиваются.
5) Давление увеличивается, а температура газа не изменяется.
7. Гелий, количество вещества которого ν = 2 моль, находившийся при температуре T = 300 К, сначала изобарно нагрели, а затем изохорно перевели в состояние с температурой, равной начальной. Определите, во сколько раз увеличился объём гелия, если алгебраическая сумма количеств полученной и отданной теплоты Q = 5 кДж.
Данная тема будет посвящена решению задач с применением первого
начала термодинамики.
Задача 1. При изотермическом расширении идеальным
одноатомным газом была совершена работа 100 Дж. Какое количество теплоты
сообщено газу?
|
ДАНО: |
РЕШЕНИЕ Согласно первому закону термодинамики, количество теплоты, Внутренняя энергия идеального газа представляет собой Так как T = Следовательно |
|
|
Ответ: количество теплоты, сообщенное
газу, равно 100 Дж.
Задача 2. При адиабатном сжатии 4 моль идеального
одноатомного газа была совершена работа внешней силы 1 кДж. Определите, на
сколько поднялась температура газа.
|
ДАНО: |
СИ |
РЕШЕНИЕ Согласно первому началу термодинамики, изменение внутренней Искомое изменение температуры |
|
|
Ответ: температура повысилась на 20 К.
Задача 3. Объем одноатомного идеального газа при
изобарном расширении увеличился на 2 л. Какое количество теплоты получил газ в
ходе расширения, если его давление равно 200 кПа?
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем уравнение, выражающее математическую запись первого Внутренняя энергия идеального газа представляет собой Работа связана с изменением объема формулой: Запишем уравнения Менделеева — Клапейрона для начального и Следовательно, изменение внутренней энергии равно Тогда количество теплоты, которое получил газ равно |
|
|
Ответ: газ получил 1 кДж теплоты.
Задача 4. Тепловой процесс, график которого изображен
на рисунке, совершают над идеальным газом, масса которого остается постоянной.
Определите, как изменялась температура газа на участках 1 — 2, 2 — 3 и 3 — 1.
На каких участках газ получал некоторое количество теплоты, а на каких отдавал?
РЕШЕНИЕ
Рассмотрим процесс 1–2. Как видно, давление газа, на этом
участке, прямо пропорционально его объему. В качестве коэффициента
пропорциональности выступает некоторая постоянная величина a.
Запишем для данного участка графика уравнение Менделеева —
Клапейрона в общем виде.
Из формулы следует, что
Так как газ расширяется, то работа больше нуля
Согласно первому закону термодинамики
Рассмотрим процесс 2–3. В этом происходит уменьшение давления
газа при неизменном объеме, то есть процесс 2–3 — изохорный. А как известно,
при изохорном процессе газ работы не совершает.
Согласно закону Шарля
Поскольку
Из первого закона термодинамики можно заключить
Рассмотрим процесс 3–1. Как видно из графика, этот процесс
характеризуется уменьшением объема газа при постоянном давлении. Значит, данный
процесс — изобарный.
Согласно закону Гей-Люссака для изобарного процесса
Поскольку
и
Согласно первому закону термодинамики
Задача 5. В теплоизолированном высоком цилиндрическом
сосуде на расстоянии h от дна висит на нити
поршень массой m. Под поршнем находится 1 моль
идеального газа. Давление под поршнем в начальный момент времени равно внешнему
давлению, температура газа Т1. Газ нагревается спиралью.
Какое количество теплоты нужно подвести к газу, чтобы поршень поднялся до
высоты 2h от дна? Трения нет, а внутренняя
энергия моля газа U = cT.
|
ДАНО: |
РЕШЕНИЕ Запишем первый закон термодинамики Работу газа можно определить, как произведение Сила внешнего давления Тогда Уравнение состояния идеального газа в начальном состоянии Давление газа после нагревания Уравнение состояния идеального газа после нагревания Температура газа после нагревания Изменение внутренней энергии газа Тогда |
|
|