Количество теплоты. Удельная теплоемкость вещества
Количеством теплоты называют количественную меру изменения внутренней энергии тела при теплообмене.
Количество теплоты — это энергия, которую тело отдает при теплообмене (без совершения работы). Количество теплоты, как и энергия, измеряется в джоулях (Дж).
Удельная теплоемкость вещества
Теплоемкость — это количество теплоты, поглощаемой телом при нагревании на $1$ градус.
Теплоемкость тела обозначается заглавной латинской буквой С.
От чего зависит теплоемкость тела? Прежде всего, от его массы. Ясно, что для нагрева, например, $1$ килограмма воды потребуется больше тепла, чем для нагрева $200$ граммов.
А от рода вещества? Проделаем опыт. Возьмем два одинаковых сосуда и, налив в один из них воду массой $400$ г, а в другой — растительное масло массой $400$ г, начнем их нагревать с помощью одинаковых горелок. Наблюдая за показаниями термометров, мы увидим, что масло нагревается быстрее. Чтобы нагреть воду и масло до одной и той же температуры, воду следует нагревать дольше. Но чем дольше мы нагреваем воду, тем большее количество теплоты она получает от горелки.
Таким образом, для нагревания одной и той же массы разных веществ до одинаковой температуры требуется разное количество теплоты. Количество теплоты, необходимое для нагревания тела и, следовательно, его теплоемкость зависят от рода вещества, из которого состоит это тело.
Так, например, чтобы увеличить на $1°$С температуру воды массой $1$ кг, требуется количество теплоты, равное $4200$ Дж, а для нагревания на $1°$С такой же массы подсолнечного масла необходимо количество теплоты, равное $1700$ Дж.
Физическая величина, показывающая, какое количество теплоты требуется для нагревания $1$ кг вещества на $1°$С, называется удельной теплоемкостью этого вещества.
У каждого вещества своя удельная теплоемкость, которая обозначается латинской буквой $с$ и измеряется в джоулях на килограмм-градус (Дж/(кг$·°$С)).
Удельная теплоемкость одного и того же вещества в разных агрегатных состояниях (твердом, жидком и газообразном) различна. Например, удельная теплоемкость воды равна $4200$ Дж/(кг$·°$С), а удельная теплоемкость льда $2100$ Дж/(кг$·°$С); алюминий в твердом состоянии имеет удельную теплоемкость, равную $920$ Дж/(кг$·°$С), а в жидком — $1080$ Дж/(кг$·°$С).
Заметим, что вода имеет очень большую удельную теплоемкость. Поэтому вода в морях и океанах, нагреваясь летом, поглощает из воздуха большое количество тепла. Благодаря этому в тех местах, которые расположены вблизи больших водоемов, лето не бывает таким жарким, как в местах, удаленных от воды.
Расчет количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении
Из вышеизложенного ясно, что количество теплоты, необходимое для нагревания тела, зависит от рода вещества, из которого состоит тело (т. е. его удельной теплоемкости), и от массы тела. Ясно также, что количество теплоты зависит от того, на сколько градусов мы собираемся увеличить температуру тела.
Итак, чтобы определить количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость тела умножить на его массу и на разность между его конечной и начальной температурами:
$Q=cm(t_2-t_1)$
где $Q$ — количество теплоты, $c$ — удельная теплоемкость, $m$ — масса тела, $t_1$ — начальная температура, $t_2$ — конечная температура.
При нагревании тела $t_2 > t_1$ и, следовательно, $Q > 0$. При охлаждении тела $t_2 < t_1$ и, следовательно, $Q < 0$.
В случае, если известна теплоемкость всего тела $С, Q$ определяется по формуле
$Q=C(t_2-t_1)$
Удельная теплота парообразования, плавления, сгорания
Теплота парообразования (теплота испарения) — количество теплоты, которое необходимо сообщить веществу (при постоянном давлении и постоянной температуре) для полного превращения жидкого вещества в пар.
Теплота парообразования равна количеству теплоты, выделяющемуся при конденсации пара в жидкость.
Превращение жидкости в пар при постоянной температуре не ведет к увеличению кинетической энергии молекул, но сопровождается увеличением их потенциальной энергии, т. к. расстояние между молекулами существенно увеличивается.
Удельная теплота парообразования и конденсации. Опытами установлено, что для полного обращения в пар $1$ кг воды (при температуре кипения) необходимо затратить $2.3$ МДж энергии. Для обращения в пар других жидкостей требуется иное количество теплоты. Например, для спирта оно составляет $0.9$ МДж.
Физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой $1$ кг в пар без изменения температуры, называется удельной теплотой парообразования.
Удельную теплоту парообразования обозначают буквой $r$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты, необходимое для парообразования (или выделяющееся при конденсации). Чтобы вычислить количество теплоты $Q$, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования $r$ умножить на массу $m$:
$Q=rm$
При конденсации пара происходит выделение такого же количества теплоты:
$Q=-rm$
Удельная теплота плавления
Теплота плавления — это количество теплоты, которое необходимо сообщить веществу при постоянном давлении и постоянной температуре, равной температуре плавления, чтобы полностью перевести его из твердого кристаллического состояния в жидкое.
Теплота плавления равна тому количеству теплоты, которое выделяется при кристаллизации вещества из жидкого состояния.
При плавлении вся подводимая к веществу теплота идет на увеличение потенциальной энергии его молекул. Кинетическая энергия не меняется, поскольку плавление идет при постоянной температуре.
Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить один килограмм льда, нужно затратить $332$ Дж энергии, а для того чтобы расплавить $1$ кг свинца — $25$ кДж.
Физическая величина, показывающая, какое количество теплоты необходимо сообщить кристаллическому телу массой $1$ кг, чтобы при температуре плавления полностью перевести его в жидкое состояние, называется удельной теплотой плавления.
Удельную теплоту плавления измеряют в джоулях на килограмм (Дж/кг) и обозначают греческой буквой $λ$ (лямбда).
Удельная теплота кристаллизации равна удельной теплоте плавления, поскольку при кристаллизации выделяется такое же количество теплоты, какое поглощается при плавлении. Так, например, при замерзании воды массой $1$ кг выделяются те же $332$ Дж энергии, которые нужны для превращения такой же массы льда в воду.
Чтобы найти количество теплоты, необходимое для плавления кристаллического тела произвольной массы, или теплоту плавления, надо удельную теплоту плавления этого тела умножить на его массу:
$Q=λm$
Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой $m$, следует пользоваться той же формулой, но со знаком «минус»:
$-Q=λm$
Удельная теплота сгорания
Теплота сгорания (или теплотворная способность, калорийность) — это количество теплоты, выделяющейся при полном сгорании топлива.
Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива. Обычное топливо (уголь, нефть, бензин) содержит углерод. При горении атомы углерода соединяются с атомами кислорода, содержащегося в воздухе, в результате чего образуются молекулы углекислого газа. Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.
Теплота сгорания топлива зависит от вида топлива и его массы. Чем больше масса топлива, тем больше количество теплоты, выделяющейся при его полном сгорании.
Физическая величина, показывающая, какое количество теплоты выделяется при полном сгорании топлива массой $1$ кг, называется удельной теплотой сгорания топлива.
Удельную теплоту сгорания обозначают буквой $q$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты $Q$, выделяющееся при сгорании $m$ кг топлива, определяют по формуле:
$Q=qm$
Чтобы найти количество теплоты, выделяющееся при полном сгорании топлива произвольной массы, нужно удельную теплоту сгорания этого топлива умножить на его массу.
Уравнение теплового баланса
В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы $∆U_i$ не может приводить к изменению внутренней энергии всей системы. Следовательно,
$∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$
Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: $∆U_i=Q_i$. Учитывая ($∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$), получим:
$Q_1+Q_2+Q_3+…+Q_n=∑↙{i}↖{n}Q_i=0$
Это уравнение называется уравнением теплового баланса. Здесь $Q_i$ — количество теплоты, полученное или отданное $i$-м телом. Любое из количеств теплоты $Q_i$ может означать теплоту, выделяемую или поглощаемую при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.
Уравнение теплового баланса является математическим выражением закона сохранения энергии при теплообмене.
Для характеристики процесса плавления вводится физическая величина «удельная теплота плавления», показывающая, как изменяется внутренняя энергия тела массой (1) кг при теплообмене.
Удельная теплота плавления обозначается
λ
(греч. буква лямбда).
Обрати внимание!
Единица измерения —
1Джкг
.
Определяют удельную теплоту плавления опытным путём.
Обрати внимание!
Чтобы рассчитать количество теплоты, необходимое для плавления кристаллического тела, нужно удельную теплоту плавления умножить на его массу.
Получим формулы для нахождения удельной теплоты плавления тела и массы тела:
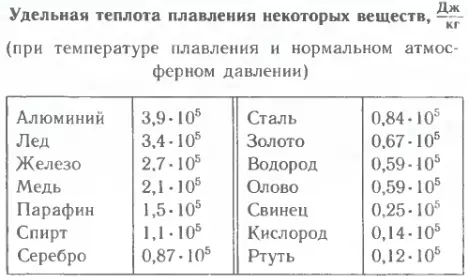
Удельная теплота плавления при нормальном атмосферном давлении некоторых веществ представлена в таблице.
|
Вещество |
Удельная теплота плавления, Джкг |
|
Алюминий |
(3,9) ⋅105 |
|
Лёд |
(3,4) ⋅105 |
|
Железо |
(2,7) ⋅105 |
|
Медь |
(2,1) ⋅105 |
|
Серебро |
(0,87) ⋅105 |
|
Сталь |
(0,84) ⋅105 |
|
Золото |
(0,67) ⋅105 |
|
Олово |
(0,59) ⋅105 |
|
Свинец |
(0,25) ⋅105 |
|
Ртуть |
(0,12) ⋅105 |
Удельная теплота плавления.
Мы
рассматривали график плавления и
отвердевания льда. Из графика видно,
что, пока лед плавится, температура его
не меняется. И лишь после того как весь
лед расплавится, температура образовавшейся
жидкости начинает повышаться. Но ведь
и во время процесса плавления лед
получает энергию от сгорающего в
нагревателе топлива. А из закона
сохранения энергии следует, что она не
может исчезнуть. На что же расходуется
энергия топлива во время плавления?
Мы знаем,
что в кристаллах молекулы (или атомы)
расположены в строгом порядке. Однако
и в кристаллах они находятся в тепловом
движении (колеблются). При нагревании
тела средняя скорость движения молекул
возрастает. Следовательно, возрастает
и их средняя кинетическая энергия и
температура. На графике это участок АВ
(см. рис. 16). Вследствие этого размах
колебаний молекул (или атомов)
увеличивается. Когда тело нагреется до
температуры плавления, то нарушится
порядок в расположении частиц в
кристаллах. Кристаллы теряют свою форму.
Вещество плавится, переходя из твердого
состояния в жидкое.
Следовательно,
вся энергия, которую получает
кристаллическое тело после того как
оно уже нагрето до температуры плавления,
расходуется на разрушение кристалла.
В связи с этим температура тела перестает
повышаться. На графике это участок BC.
Опыты
показывают, что для превращения различных
кристаллических веществ одной и той же
массы в жидкость при температуре
плавления требуется разное количество
теплоты.
Физическая
величина, показывающая, какое количество
теплоты необходимо сообщить кристаллическому
телу массой 1 кг, чтобы при температуре
плавления полностью перевести его в
жидкое состояние, называется удельной
теплотой плавления.
Удельную
теплоту плавления обозначают А (греч.
буква «лямбда» ). Ее единица — 1

Определяют удельную теплоту плавления
на опыте. Так, было установлено, что
удельная теплота плавления льда равна
3,4 • 10⁵

Это
означает, что для превращения куска
льда массой 1 кг, взятого при 0 ˚C, в воду
такой же температуры требуется затратить
3,4 • 10⁵ Дж энергии. А чтобы расплавить
брусок из свинца массой 1 кг, взятого
при его температуре плавления, потребуется
затратить 2,5 • 10⁴ Дж энергии.
Следовательно,
при температуре плавления внутренняя
энергия вещества в жидком состоянии
больше внутренней энергии такой же
массы вещества в твердом состоянии.
Чтобы
вычислить количество теплоты Q, необходимое
для плавления кристаллического тела
массой m, взятого при его
температуре плавления и нормальном
атмосферном давлении, нужно удельную
теплоту плавления λ умножить на массу
тела m: Q =λm.
Опыты
показывают, что при отвердевании
кристаллического вещества выделяется
точно такое же количество теплоты,
которое поглощается при его плавлении.
Так, при отвердевании воды массой 1 кг
при температуре 0 ˚C выделяется количество
теплоты, равное 3,4 • 10⁵ Дж. Точно такое
же количество теплоты требуется и для
плавления льда массой 1 кг при температуре
0 ˚C.
При
отвердевании вещества все происходит
в обратном порядке.
Средняя
кинетическая энергия и скорость молекул
в охлажденном расплавленном веществе
уменьшаются. Силы притяжения теперь
могут удерживать медленно движущиеся
молекулы друг около друга. Вследствие
этого расположение частиц становится
упорядоченным — образуется кристалл.
Выделяющаяся при кристаллизации энергия
расходуется на поддержание постоянной
температуры. На графике это участок EF.
Кристаллизация
облегчается, если в жидкости с самого
начала присутствуют какие-либо посторонние
частицы, например пылинки. Они становятся
центрами кристаллизации. В обычных
условиях в жидкости имеется множество
центров кристаллизации, около которых
и происходит образование кристалликов.
При кристаллизации происходит выделение
энергии и передача ее окружающим телам.
Количество теплоты, выделяющееся при
кристаллизации тела массой m,
определяется также по формуле :Q =λm.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В процессе плавления температура вещества не изменяется Вся получаемая им энергия при этом тратится на разрушение кристаллической решетки и увеличение потенциальной энергии молекул тела.
Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить 1 кг льда, нужно затратить 332 кДж энергии, а для того чтобы расплавить 1 кг свинца — 25 кДж.
Физическая величина, показывающая, какое количество теплоты необходимо для превращения 1 кг кристаллического вещества, взятого при температуре плавления, в жидкость той же температуры, называется удельной теплотой плавления.
Удельную теплоту плавления измеряют в джоулях на килограмм (Дж/кг) и обозначают греческой буквой λ (ламбда):
λ — удельная теплота плавления.
При кристаллизации вещества потенциальная энергия молекул уменьшается и в окружающую среду выделяется точно такое же (по модулю) количество теплоты, что и поглощается при его плавлении. Поэтому, например, при замерзании воды массой 1 кг выделяются те же 332 кДж энергии, которые нужны для превращения такой же массы льда в воду.
Удельную теплоту плавления различных веществ можно найти в таблице 10.
Из этой таблицы, например, видно, что удельная теплота плавления меди λ = 2,1 * 105 Дж/кг. Это число показывает, что для плавления 1 кг меди требуется затратить 2,1 * 105 Дж энергии; точно такое же (по модулю) количество теплоты будет выделено 1 кг жидкой меди при ее кристаллизации.
Для плавления 2 кг меди потребуется в 2 раза больше энергии, для плавления 3 кг меди — в 3 раза больше и т. д.
Чтобы найти количество теплоты, необходимое для плавления кристаллического тела произвольной массы, надо удельную теплоту плавления этого тела умножить на его массу:
Q = λm. (39.1)
Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой m, следует пользоваться той же формулой, но со знаком «минус»:
Q = –λm. (39.2)
Следует помнить, что формулы (39.1) и (39.2) можно применять только к таким телам, которые уже имеют температуру, равную температуре плавления. Если же она отличается от нее, то предварительно следует рассчитать то количество теплоты, которое необходимо для нагревания тела или которое выделяется телом при его охлаждении.
1. Что называется удельной теплотой плавления тела? 2. Удельная теплота плавления золота равна 67 кДж/кг. Что показывает это число? 3. По какой формуле вычисляют количество теплоты, необходимое для плавления тела? 4. По какой формуле вычисляют количество теплоты, выделяющееся при кристаллизации вещества?
Вы уже познакомились с несколькими уроками, основная тема которых — это явление плавления: “Плавление и отвердевание кристаллических тел”, “График плавления и отвердевания кристаллических тел”, “Удельная теплота плавления”.
В данном уроке для решения задач вам пригодятся вышеупомянутые материалы. Также мы будем использовать данные формулы:
- $Q = cm(t_2 — t_1)$
- $Q = qm$
- $eta = frac{A_п}{A_з}$
- $A = Fs$
Табличные значения различных величин вы можете найти в следующих уроках:
- Плотность
- Удельная теплоемкость
- Энергия топлива. Удельная теплота сгорания
- Удельная теплота плавления
Задача №1
Кусок алюминия массой $10 space кг$, взятый при температуре плавления $660 degree C$, полностью расплавился. Какое для этого потребовалось количество теплоты?
Дано:
$m = 10 space кг$
$t = 660 degree C$
$lambda = 8.9 cdot 10^5 frac{Дж}{кг}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Так как тело взято при его температуре плавления $t = 660 degree C$, нужно рассчитать количество теплоты, необходимое для плавления кристаллического тела, по формуле:
$Q = lambda m$,
$Q = lambda = 8.9 cdot 10^5 frac{Дж}{кг} cdot 10 space кг = 8.9 cdot 10^6 space Дж = 8.9 space МДж$.
Ответ: $Q = 8.9 space МДж$.
Задача №2
Во сколько раз больше теплоты идет на плавление $2 space кг$ чугуна, чем на нагревание чугуна той же массы на $1 degree C$? Удельная теплота плавления чугуна $96 frac{кДж}{кг}$.
Дано:
$lambda = 96 frac{кДж}{кг}$
$m = 2 space кг$
$Delta t = 1 degree C$
$c = 540 frac{Дж}{кг cdot degree C}$
СИ:
$lambda = 96 cdot 10^3 frac{Дж}{кг}$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, необходимое для того, чтобы расплавить $2 space кг$ чугуна:
$Q_1 = lambda m$,
$Q_1 = 96 cdot 10^3 frac{Дж}{кг} cdot 2 space кг = 192 cdot 10^3 space Дж$.
Теперь рассчитаем количество теплоты, необходимое для нагревания на $1 degree C$ чугуна той же массы:
$Q_2 = cm(t_2 — t_1) = cm Delta t$,
$Q_2 = 540 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 1 degree C = 1080 space Дж = 1.08 cdot 10^3 space Дж$.
Теперь мы можем сравнить эти энергии:
$frac{Q_1}{Q_2} = frac{192 cdot 10^3 space Дж}{1.08 cdot 10^3 space Дж} approx 178$.
Значит, количество теплоты, необходимое для плавления $2 space кг$ чугуна, в 178 раз больше количества теплоты, необходимого для нагревания чугуна той же массы на $1 degree C$.
Ответ: в 178 раз.
Задача №3
На рисунке 1 дан график изменения температуры твердого тела при нагревании.
Определите по этому графику:
- При какой температуре плавится это тело?
- Как долго длилось нагревание от $60 degree C$ до точки плавления?
- Как долго длилось плавление?
- До какой температуры было нагрето вещество в жидком состоянии?
Показать решение и ответ
Скрыть
Решение:
- Из графика видно, что тело нагревается до $80 degree C$. С этой температуры последующий участок графика параллелен оси времени. При этом температура так и остается равной $80 degree C$.
Значит, на этом участке графика идет процесс плавления с температурой $80 degree C$ - Тело достигает температуры $60 degree C$ в момент времени $T_1 = 2 space мин$. Температуры плавления в $80 degree C$ тело достигает в момент времени $T_2 = 6 space мин$.
Тогда нагревание длилось $T_2 — T_1 = 6 space мин — 2 space мин = 4 space мин$ - Вернемся к участку плавления (он параллелен оси времени). Плавление началось в момент времени $T_1 = 6 space мин$, а закончилось в момент времени $T_2 = 8 space мин$.
Значит, плавление длилось $T_2 — T_1 = 8 space мин — 6 space мин = 2 space мин$ - После завершения процесса плавления вещество, из которого состояло тело, перешло в жидкое состояние. График снова пошел наверх — это означает, что жидкость нагревается. Самая верхняя точка графика соответствует наивысшей температуре жидкости $t approx 87.5 degree C$.
Ответ: 1. $80 degree C$,
2. $4 space мин$,
3. $2 space мин$,
4. $87.5 degree C$.
Задача №4
Определите объем глицерина, если при его кристаллизации выделилось $240 space кДж$ энергии. Плотность глицерина $1200 frac{кг}{м^3}$, удельная теплота плавления $1.99 cdot 10^5 frac{Дж}{кг}$.
Дано:
$Q = 240 space кДж$
$lambda = 1.99 cdot 10^5 frac{Дж}{кг}$
$rho = 1200 frac{кг}{м^3}$
СИ:
$Q = 240 cdot 10^3 space Дж$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Известно, что кристаллизация (отвердевание) и плавление происходят при одинаковой температуре для одного и того же вещества. Если при плавлении требуется сообщить телу определенную энергию, то при кристаллизации она выделяется.
Соответственно, для того, чтобы вычислить количество энергии, которое выделится при отвердевании тела, мы используем ту же формулу, что и для ситуаций с плавлением:
$Q = lambda m$.
Выразим массу через объем и плотность и подставим ее в формулу:
$m = rho V$,
$Q = lambda rho V$.
Выразим отсюда объем и рассчитаем его:
$V = frac{Q}{lambda rho}$,
$V = frac{240 cdot 10^3 space Дж}{1.99 cdot 10^5 frac{Дж}{кг} cdot 1200 frac{кг}{м^3}} approx 0.1 cdot 10^{-2} space м^3 approx 1 cdot 10^{-3} space м^3 approx 1 space л$.
Ответ: $V approx 1 space л$.
Задача №5
Определите плотность льда при температуре $0 degree C$, если известно, что для плавления льда объемом $1 space дм^3$ требуется количество теплоты, равное $301.5 space кДж$.
Дано:
$V = 1 space дм^3$
$Q = 301.5 space кДж$
$t = 0 degree C$
$lambda = 3.4 cdot 10^5 frac{Дж}{кг}$
СИ:
$V = 1 cdot 10^{-3} space м^3$
$Q = 301.5 cdot 10^3 space Дж$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Количество теплоты, необходимое для плавления льда:
$Q = lambda m$.
В задаче говорится, что «для плавления требуется количество теплоты». Это означает, что лед уже находится при температуре плавления, т. е. при $0 degree C$. Значит, мы будем искать плотность того самого льда, для которого у нас есть все необходимые данные.
Выразим массу льда через плотность и объем и подставим в вышеприведенную формулу:
$m = rho V$,
$Q = lambda rho V$.
Выразим отсюда плотность льда и рассчитаем ее:
$rho = frac{Q}{lambda V}$,
$rho = frac{301.5 cdot 10^3 space Дж}{3.4 cdot 10^5 frac{Дж}{кг} cdot 1 cdot 10^{-3} space м^3} approx 887 frac{кг}{м^3}$.
Ответ: $rho approx 887 frac{кг}{м^3}$.
Задача №6
На рисунке 2 изображены графики зависимости температуры от времени для слива свинца (I) и плитка олова (II) одинаковой массы. Количество теплоты, получаемой каждым телом в единицу времени, одинаково.
Определите по графику:
- У какого слитка температура плавления выше?
- Какой металл обладает большей удельная теплоемкость?
- У какого металла больше удельная теплота плавления?
Показать решение и ответ
Скрыть
Решение:
- Определим из графика температур плавления для обоих слитков. Обратите внимание, что участку плавления соответствует участок графика, параллельный оси времени. Так, для свинца (I) температура плавления равна $327 degree C$, а для олова (II) — $232 degree C$.
Значит, температура плавления свинца выше, чем температура плавления олова - В условии задачи сказано, что количество теплоты, получаемое каждым телом в единицу времени, одинаково. Удельная теплоемкость же определяется количеством энергии, которую нужно сообщить телу, чтобы изменить его температуру на $1 degree C$.
Взгляните на участки графиков, когда тела нагреваются, например, до температуры $232 degree C$. Отчетливо видно, что свинец (I) достигнет этой температуры быстрее.
Это означает, что ему потребовалось меньше энергии, чтобы достигнуть этой температуры. Следовательно, и для изменения температуры на $1 degree C$ ему требуется меньшее количество теплоты, чем олову (II). Значит, удельная теплоемкость свинца меньше, чем удельная теплоемкость олова - Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить телу при температуре плавления, чтобы полностью перевести его из твердого в жидкое состояние.
Значит, нам нужно обратиться к участкам графиков, на которых происходит плавление (они параллельны оси времени). Видно, что участок плавления олова (II) намного длиннее такого же участка для свинца (I).
Так как тела имеют одинаковую массу и получают одинаковое количество теплоты в единицу времени, очевидно, что олову для перехода в жидкое состояние потребовалось больше энергии, чем свинцу.
Это означает, что удельная теплота плавления олова больше удельной теплоты плавления свинца
Ответ:1. у свинца, 2. у олова, 3. у олова.
Задача №7
В $5 space кг$ воды при температуре $40 degree C$ опустили $3 space кг$ льда. Сколько льда растает?
Дано:
$m_в = 5 space кг$
$t_1 = 40 degree C$
$m_л = 3 space кг$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$lambda_л = 3.4 cdot 10^5 frac{Дж}{кг}$
$m_{л1} — ?$
Показать решение и ответ
Скрыть
Решение:
Когда лед опустили в воду, между двумя этими телами начался теплообмен. Он будет продолжаться до тех пор, пока их температуры не станут равны друг другу. В этот момент между телами установится равновесие.
Вода будет охлаждаться и выделять некоторое количество теплоты, которое будет идти на плавление льда при $0 degree C$. Так будет продолжаться до тех пор, пока температура воды не станет равной $ degree C$. Теплообмен завершится.
Далее, если воде не будет сообщаться никакой энергии, она начнет отвердевать. Избыточная энергия будет идти на поддержание температуры на одном уровне до окончания процесса кристаллизации.
Итак, давайте рассчитаем, какое количество энергии выделится при охлаждении воды с $t_1 = 40 degree C$ до $0 degree C$:
$Q_в = c_в m_в(t_2 — t_1)$,
$Q_в = 4200 frac{Дж}{кг cdot degree C} cdot 5 space кг cdot (40 degree C — 0 degree C = 21 cdot 10^3 frac{Дж}{degree C} cdot 40 degree C = 840 cdot 10^3 space Дж$.
А теперь рассчитаем количество теплоты, которое необходимо сообщить льду, чтобы он полностью расплавился:
$Q_л = lambda_л m_л$,
$Q_л = 3.4 cdot 10^5 frac{Дж}{кг} cdot 3 space кг = 10.2 cdot 10^5 space Дж = 1020 cdot 10^3 space Дж$.
Получается, что $Q_в < Q_л$. Это означает, что лед не сможет полностью расплавиться.
Но какая-то его часть расплавится. Теперь нам нужно рассчитать, какая масса льда расплавится, если ей сообщить количество теплоты $Q_в$:
$Q = Q_в = lambda_л m_{л1}$.
Выразим отсюда массу льда и рассчитаем ее:
$m_{л1} = frac{Q_в}{lambda_л}$,
$m_{л1} = frac{840 cdot 10^3 space Дж}{3.4 cdot 10^5 frac{Дж}{кг}} approx 2.47 space кг$.
Ответ: $m_{л1} approx 2.47 space кг$.
В медный калориметр весом $200 space г$ налито $100 space г$ воды при $16 degree C$ для обоих тел. В воду бросили кусочек льда при $0 degree C$ весом $9.3 space г$, который целиком расплавился. Окончательная температура воды и калориметра после этого установилась $9 degree C$. Определите на основании этих данных удельную теплоту плавления льда.
Дано:
$m_м = 200 space г$
$m_в = 100 space г$
$m_л = 9.3 space г$
$t_в = 16 degree C$
$t_л = 0 degree C$
$t = 9 degree C$
$c_м = 400 frac{Дж}{кг cdot degree C}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
СИ:
$m_м = 0.2 space кг$
$m_в = 0.1 space кг$
$m_л = 0.0093 space кг$
$lambda_л — ?$
Показать решение и ответ
Скрыть
Решение:
Изначально медный калориметр и вода находились в равновесии и имели одинаковую температуру $16 degree C$. Когда в воду опустили кусочек льда, между всеми этими телами начался теплообмен.
Калориметр и вода начали охлаждаться и выделять энергию. За счет этой энергии лед начал плавится. Когда лед полностью расплавился, теплообмен еще не закончился. Вода и калориметр продолжили охлаждаться до какой-то температуры, которой достиг бывший лед в виде жидкости. Температура выровнялась и стала равна $9 degree C$.
Таким образом, медный калориметр и вода при охлаждении с $16 degree C$ до $9 degree С$ выделили такое количество теплоты, которого хватило на плавление льда и его нагревание от $0 degree C$ до $9 degree C$. Так как вода и калориметр выделяли энергию, разницу температур запишем наоборот $(t_в — t)$, чтобы компенсировать отрицательный знак количества теплоты.
Запишем это формулой:
$Q_м + Q_в = Q_{пл} + Q_л$,
$c_м m_м (t_в — t) + c_в m_в (t_в — t) = lambda_л m_л + c_в m_л (t — t_л)$.
Обратите внимание, что $Q_л$ определяется через удельную теплоемкость воды, ведь лед к этому моменту находится в жидком состоянии.
Теперь постепенно выразим отсюда удельную теплоту плавления льда:
$lambda_л m_л = c_м m_м (t_в — t) + c_в m_в (t_в — t) — c_в m_л (t — t_л)$,
$lambda_л = frac{c_м m_м (t_в — t) + c_в m_в (t_в — t) — c_в m_л (t — t_л)}{m_л}$, или
$ lambda_л = frac{Q_м + Q_в — Q_л} {m_л}$.
Сначала рассчитаем величины $Q_м$, $Q_в$ и $Q_л$ по отдельности, а затем подставим их значения в формулу для расчета удельной теплоты плавления льда.
Количество теплоты, которое выделит медный калориметр при охлаждении:
$Q_м = c_м m_м (t_в — t) = 400 frac{Дж}{кг cdot degree C} cdot 0.2 space кг cdot (16 degree C — 9 degree C) = 80 frac{Дж}{degree C} cdot 7 degree = 560 space Дж$.
Количество теплоты, которое выделит вода при охлаждении:
$Q_в = c_в m_в (t_в — t) = 4200 frac{Дж}{кг cdot degree C} cdot 0.1 space кг cdot (16 degree C — 9 degree C) = 420 frac{Дж}{degree C} cdot 7 degree C = 2940 space Дж$.
Количество теплоты, затраченное на нагревание воды (растаявшего льда):
$Q_л = c_в m_л (t — t_л) = 4200 frac{Дж}{кг cdot degree C} cdot 0.0093 space кг cdot (9 degree C — 0 degree C) = 39.06 frac{Дж}{degree C} cdot 9 degree C = 351.54 space Дж$.
Теперь можем рассчитать удельную теплоту плавления льда:
$lambda_л = frac{560 space Дж + 2940 space Дж — 351.54 space Дж} {0.0093 space кг} = frac{3148.46 space Дж}{0.0093 space кг} approx 338 space 544 frac{Дж}{кг} approx 3.4 cdot 10^5 frac{Дж}{кг}$.
Так мы рассчитали удельную теплоту плавления льда. Она оказалась равна табличному значению, значит, расчеты выполнены верно.
Ответ: $lambda_л approx 3.4 cdot 10^5 frac{Дж}{кг}$.
Задача №9
Сколько требуется сжечь каменного угля в печи, чтобы расплавить $100 space т$ чугуна, взятого при температуре $20 degree C$, если КПД печи составляет $40 %$? Удельная теплота плавления чугуна $0.96 cdot 10^5 frac{Дж}{кг}$
Дано:
$m_ч = 100 space т$
$lambda_ч = 0.96 cdot 10^5 frac{Дж}{кг}$
$c_ч = 540 frac{Дж}{кг cdot degree C}$
$t_1 = 20 degree C$
$t_{пл} = t_2 = 1200 degree C$
$q_у = 2.7 cdot 10^7 frac{Дж}{кг}$
$eta = 40 % = 0.4$
Показать решение и ответ
Скрыть
Решение:
Для того,чтобы расплавить чугун, сначала его нужно нагреть до температуры плавления, а потом уже сообщить какое-то количество теплоты, необходимое для его плавления:
$Q_ч = Q_1 + Q_2 = c_ч m_ч (t_2 — t_1) + lambda_ч m_ч$.
Рассчитаем это количество теплоты:
$Q_ч = 540 frac{Дж}{кг cdot degree C} cdot 100 cdot 10^3 space кг cdot (1200 degree C — 20 degree C) + 0.96 cdot 10^5 frac{Дж}{кг} cdot 100 cdot 10^3 space кг = 637.2 cdot 10^8 space Дж + 96 cdot 10^8 space Дж = 733.2 cdot 10^8 space Дж$.
Запишем формулу для КПД:
$eta = frac{A_п}{A_з} = frac{Q_ч}{Q_у}$,
где $Q_ч$ — это количество теплоты, необходимое для того, чтобы нагреть и расплавить чугун, а $Q_у$ — количество теплоты, которое выделится при сгорании каменного угля.
Выразим отсюда $Q_у$:
$Q_у = frac{Q_ч}{eta}$.
С другой стороны, у нас есть формула для расчета количества теплоты, которое выделится при сгорании топлива:
$Q_у = q_у m_у$.
Выразим отсюда массу каменного угля и подставим найденные выражения для количества теплоты через формулу для КПД:
$m_у = frac{Q_у}{q_у} = frac{frac{Q_ч}{eta}}{q_у} = frac{Q_ч}{eta cdot q_у}$.
Рассчитаем эту массу:
$m_у = frac{733.2 cdot 10^8 space Дж}{0.4 cdot 2.7 cdot 10^7 frac{Дж}{кг}} = 6789 space кг approx 6.8 space т$.
Ответ: $m_у approx 6.8 space т$.
Задача №10
В водопаде высотой $32 space м$ ежесекундно падает $3.5 space м^3$ воды. Какое количество энергии можно получить в час от этого водопада? Какое количество каменного угля нужно сжигать каждый час, чтобы получить то же самое количество энергии?
Дано:
$t = 1 space ч$
$V = 3.5 space м^3$
$h = 32 space м$
$q = 2.7 cdot 10^7 frac{Дж}{кг}$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$t = 3600 space с$
$Q — ?$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Количество теплоты (энергия) является эквивалентом работы. Работа же по определению:
$A = Fs$.
Вода падает вниз под действием силы тяжести. Значит, сила тяжести = это та сила, которая совершает работу по перемещению воды на некоторое расстояние. Расстояние $s$ в нашем случае — это высота водопада $h$.
Тогда мы можем записать:
$Q = A = F_{тяж}h = mgh$.
По этой формуле мы рассчитаем энергию, которую можно получить в одну секунду. Чтобы узнать энергию за час, добавим множитель времени 3600:
$Q = mgh cdot 3600$.
Масса воды нам неизвестна. Выразим ее через объем и плотность и подставим в нашу формулу:
$m = rho V$,
$Q = rho Vgh cdot 3600$.
Рассчитаем эту энергию:
$Q = 1000 frac{кг}{м^3} cdot 3.5 space м^3 cdot 9.8 frac{Н}{кг} cdot 32 space м cdot 3600 approx 3.95 cdot 10^9 space Дж approx 3.95 space ГДж$.
Теперь рассчитаем, какая масса каменного угля при сжигании дает столько же энергии:
$Q = qm$,
$m = frac{Q}{q}$,
$m = frac{3.95 cdot 10^9 space Дж}{2.7 cdot 10^7 frac{Дж}{кг}} approx 146 space кг$.
Ответ: $Q approx 3.95 space ГДж$, $m approx 146 space кг$.