Тема: найти количество теплоты, выделившейся при этом соударении (Прочитано 5981 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Тело массой m = 3 кг движется со скоростью υ1 = 4 м/с и ударяется о неподвижное тело такой же массы. Считая соударение тел абсолютно неупругим, найти количество теплоты, выделившейся при этом соударении. Сделать рисунок.
« Последнее редактирование: 28 Декабря 2014, 16:58 от Сергей »
Записан
Решение.
В случае абсолютно неупругого удара закон сохранения импульса принимает вид:
[ begin{align}
& {{m}_{1}}cdot vec{upsilon }=({{m}_{1}}+{{m}_{2}})cdot vec{upsilon }, \
& {{m}_{1}} ={{m}_{2}}=m, mcdot vec{upsilon }=2cdot mcdot vec{upsilon } (1). \
end{align} ]
Покажем рисунок, найдем проекции на ось Х и выразим скорости шаров после неупругого взаимодействия:
[ mcdot {{upsilon }_{1}}=2cdot mcdot upsilon , upsilon =frac{{{upsilon }_{1}}}{2} (2). ]
Запишем закон сохранения энергии для неупругого столкновения двух тел:
[ frac{mcdot upsilon _{1}^{2}}{2}=frac{2cdot mcdot upsilon _{{}}^{2}}{2}+Q (3). ]
Решим систему уравнений (2) и (3), из (2) выразим υ и подставим в (3) и определим Q:
[ Q =frac{mcdot upsilon _{1}^{2}}{4}. ]
Ответ: 12,0 Дж.
« Последнее редактирование: 07 Января 2015, 11:43 от alsak »
Записан
Шары массами 6 и 4 кг, движущиеся навстречу друг другу со скоростью 2 м/с каждый относительно Земли, соударяются, после чего движутся вместе. Определите, какое количество теплоты выделится в результате соударения.
Спрятать решение
Решение.
Согласно закону сохранения импульса
Отсюда скорость шаров после удара:
Согласно закону сохранения энергии можно найти выделявшееся количество теплоты как изменение кинетической энергии системы тел до и после взаимодействия:
Отсюда:
Ответ: 19,2 Дж.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное правильное решение, включающее следующие элементы:
1) верно записано краткое условие задачи; 2) записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом; 3) выполнены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение «по частям» (с промежуточными вычислениями). |
3 |
| Правильно записаны необходимые формулы, проведены вычисления, и получен ответ (верный или неверный), но допущена ошибка в записи краткого условия или переводе единиц в СИ.
ИЛИ Представлено правильное решение только в общем виде, без каких-либо числовых расчётов. ИЛИ Записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, но в математических преобразованиях или вычислениях допущена ошибка. |
2 |
| Записаны и использованы не все исходные формулы, необходимые для решения задачи.
ИЛИ Записаны все исходные формулы, но в одной из них допущена ошибка. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Раздел кодификатора ФИПИ:
Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
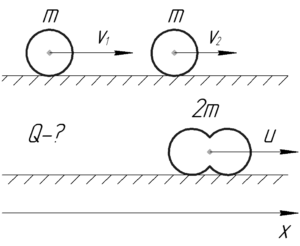
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
Ответ: .
Объяснение:
Да, для начала надо применить закон сохранения импульса (ЗСИ):
(обозначим скорости тел, как и
;
— общая скорость после столкновения)
ЗСИ:
(так как в дальнейшем нам понадобится общая скорость).
Теперь, найдём кинетическую энергию, до столкновения:
Затем найдём кинетическую энергию после столкновения:
И кол — во теплоты равно:
KZ
Kate Zhivetina
если столкновение неупругое, то сумма кинетических (масса*скорость в квадрате2) энергий шаров превратится (как в сказке) в тепло ку .


