Условие задачи:
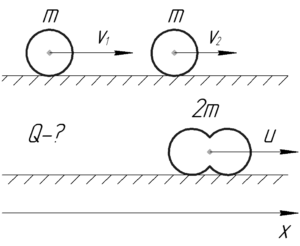
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
Начиная с определений импульса и объяснения законов сохранения, в статье показывается способ решения ряда задач, в которых важно только начальное и конечное состояние (но, например, ничего нельзя сказать про время движения), в частности, задач на столкновение тел.
Введение
С помощью законов сохранения многие механические задачи решаются намного проще, чем при использовании динамических уравнений движений. С другой стороны, законами сохранения можно пользоваться только в тех случаях, когда необходимо, зная начальное состояние тела, найти конечное. При данном описании системы невозможно узнать время движения тела и все промежуточные состояния.
Для лучшего понимания темы различных соударений давайте еще раз повторим теорию по законам сохранения в механике.
Самыми распространенными законами сохранения является закон сохранения импульса и энергии.
Импульс
Определение. Импульсом p тела (материальной точки) называется векторная физическая величина, равная произведению массы m на скорость (здесь и далее жирным шрифтом выделены векторные величины).
p = mv.
Изменение импульса можно представить через второй закон Ньютона:
Δp = mΔv = FΔt
Если рассмотреть систему материальных точек, которые движутся с разными скоростями, то импульс задается следующим выражением:
p = m₁v₁+ m₂v₂ + …
Закон сохранения импульса
При отсутствии внешних сил импульс системы материальных точек сохраняется.
Замечание 1. Отсутствие внешних сил означает, что система замкнута.
Замечание 2. Часто в задачах есть внешние силы, но при этом законом сохранения импульса в каком-то виде пользоваться можно.
- Внешние силы есть, но они взаимно скомпенсированы (например сила тяжести и сила нормальной реакции опоры при движении по гладкой поверхности).
- Внешние силы не имеют проекции на какую-то заданную ось (например, ось ОX), тогда импульс может сохраняться вдоль этого направления.
- Если в некоторый момент времени внутренние силы много больше внешних, тогда импульс системы сохраняется (например, разрыв снаряда)
Так как задачи только на закон сохранения достаточно однообразные, то рассмотрим и закон сохранения энергии.
Работа и энергия
Любая механическая система характеризуется скалярной величиной E — энергией, которая однозначно определяет состояние системы. Зная энергию системы в двух состояниях, можно найти работу внешних сил, совершенную над системой:
ΔE = E₂ – E₁ = A.
Механическая работа
Определение. Если на тело, движущееся по прямой, действует постоянная сила F, то механической работой A этой силы на перемещение s называется скалярное произведение
A = (F, s) = |F||s| · cos(α) = Fs · cos(α),
где α — угол между векторами F и s.
Определение. Средняя мощность <P> силы F — это отношение работы А, совершенной силой F за время t, к интервалу времени t.
<P> = A / t.
Мощность также можно переписать так: <P> = Fv · cos(α).
Консервативные и диссипативные силы
Определение.Консервативные силы (потенциальные силы) —это силы, работа которых при перемещении из состояния 1 в состояние 2 не зависит от траектории, а зависит только от начального и конечного положения точек 1 и 2.
Примеры.Работа силы тяжести или электростатических сил не зависит от траектории, следовательно, это консервативные силы.
К диссипативным силам относятся различные виды силы трения.
Замечание. Работа диссипативных сил всегда отрицательна. Следовательно, они уменьшают механическую энергию тела, переводя ее в тепло.
Кинетическая и потенциальная энергия
Определение. Кинетическая энергия тела равна произведению массы тела на квадрат скорости, деленное на два:
Eкин = mv² / 2.
Так как работа консервативных сил зависит только от начального и конечного положения, то для нее можно определить потенциальную энергию.
Потенциальная энергия для силы тяжести определяется следующим выражением:
Eпот = mgh.
Замечание. Для силы тяжести можно легко вывести потенциальную энергию, зная работу силы притяжения.
Другие примеры.Зная силу растяжения или сжатия пружины, легко посчитать потенциальную энергию сжатой (растянутой) пружины:
Eпот = k(x₂ – x₁)² / 2.
Закон сохранения и изменения энергии
Формулировка. Механическая энергия в замкнутой системе сохраняется при отсутствии диссипативных сил:
ΔE = 0
Замечание 1. Механической энергией называется сумма потенциальной и кинетической энергии.
E = Eкин + Епот.
Замечание 2.При наличии консервативных сил может меняться скорость тела (системы тел) и их общая кинетическая энергия, но это будет происходить за счет перехода кинетической энергии в потенциальную.
Формулировка. Изменение механической энергии под действием внешних и внутренних неконсервативных сил равно суммарной работе этих сил А:
ΔE = A.
Теорема об изменении кинетической энергии
Формулировка. Работа всех сил (консервативных и диссипативных) равна изменению кинетической энергии системы.
∑A = ΔEкин.
Замечание. С помощью этой теоремы легко решать многие задачи. Например, рассмотрим задачу о нахождении тормозного пути автомобиля, движущегося со скоростью v = 60 км/ч по дороге с коэффициетом трения μ = 0,5.
Работа силы трения:
A = –μN = –μmgS,
где N — сила нормальной реакции, S — тормозной путь автомобиля.
Изменение кинетической энергии:
ΔE = –mv² / 2.
По теореме о изменении кинетической энергии:
–mv² / 2 = –μmgS.
S = v² / 2gμ = 29 м
Замечание.Скорость необходимо перевести в СИ.
Соударения
Определение. Центральный удар — это соударение 2 тел , при котором скорости каждого из тел направлены вдоль линии, соединяющей центры обоих тел.
Замечание. Если один из шаров покоится, то скорость второго тела должна быть направлена вдоль линии, соединяющей центры тел.
При решении задач на столкновение двух и более тел надо привыкнуть к следующим формулировкам:
- Абсолютно упругий удар (упругий удар) — это тип соударения, при котором выполняется закон сохранения энергии и закон сохранения импульса. Часто этот тип соударения применим к железным шарикам.
- Неупругий удар — это удар, при котором выполняется закон сохранения импульса и закон изменения механической энергии (так как теряется часть энергии при ударе).
- Абсолютно неупругий удар — это удар, при котором два тела продолжают двигаться как единое целое. При этом столкновении выполняется закон сохранения импульса и закон изменения механической энергии.
Замечание. Как мы видим, для решения задач нужно сначала записать соответствующие законы сохранения энергии и импульса или изменения энергии. Далее необходимо решить получившуюся систему уравнений.
Задача 1
Железный шар массы m = 500 г движется по гладкой горизонтальной поверхности со скоростью 10 м/с и сталкивается с неподвижным восковым шаром, имеющим массу М = 200 г, после чего оба шара движутся вместе. Найдите количество теплоты, выделившееся при ударе.
Решение. В этой задаче удар абсолютно неупругий, поэтому выполняется закон сохранения импульса (ЗСИ) и изменения энергии.
Запишем ЗСИ на ось OX:
mv = (m + M)V. (1)

Для того, чтобы найти выделившуюся энергию при соударении, необходимо записать закон изменения энергии (ЗИЭ)
ΔE = mv² / 2 — (m + M)V² / 2. (2)
Далее остается только математическая часть задачи — решить систему уравнений (1) и (2). Из (1) найдем V:
V = mv / (M + m).
Подставив в (2), получим:

Замечание. Такую задачу невозможно решить для неупругого удара, при котором тела не слипаются друг с другом, так как нам будет неизвестны скорости двух разлетевшихся тел.
Список литературы
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
stepanka |
Заголовок сообщения: Найти количество теплоты, выделившейся в момент удара.
|
||
|
Шар массой m=1 кг, катящийся без скольжения, ударился о стенку и отскакивает от нее. Скорость шара до удара 10 м/с, а после удара 8 м/с. Найти количество теплоты, выделившейся в момент удара.
|
||
| Вернуться к началу |
|
||
|
SayHello |
Заголовок сообщения: Re: Найти количество теплоты, выделившейся в момент удара.
|
|
[math]Q = frac{{mv_1^2}}{2} — frac{{mv_2^2}}{2} = frac{m}{2}(v_1^2 — v_2^2) = 0,5(100 — 64) = 18[/math] Джоулей
|
|
| Вернуться к началу |
|
| За это сообщение пользователю SayHello «Спасибо» сказали: stepanka |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти количество теплоты
в форуме Молекулярная физика и Термодинамика |
ilya707 |
0 |
363 |
10 дек 2018, 16:58 |
|
Вычислить количество теплоты
в форуме Электричество и Магнетизм |
TORT1 |
0 |
526 |
20 мар 2014, 20:09 |
|
Вычислить количество теплоты
в форуме Электричество и Магнетизм |
TORT1 |
0 |
645 |
18 мар 2014, 22:04 |
|
Количество теплоты, сообщённое газу
в форуме Молекулярная физика и Термодинамика |
Sergey1207 |
1 |
682 |
07 янв 2019, 08:09 |
|
Количество теплоты в нагр. элементе с сопротивлением 80 Ом
в форуме Электричество и Магнетизм |
ilya707 |
1 |
645 |
10 дек 2018, 17:03 |
|
Какое количество теплоты выделится при соединении двух шаров
в форуме Электричество и Магнетизм |
Dante2886 |
7 |
757 |
02 янв 2017, 20:25 |
|
Центр удара
в форуме Интересные задачи участников форума MHP |
wrobel |
0 |
271 |
14 сен 2020, 13:10 |
|
Уравнения определения точки удара
в форуме Аналитическая геометрия и Векторная алгебра |
DDONN |
0 |
213 |
26 янв 2015, 14:22 |
|
Найти момент инерции
в форуме Интегральное исчисление |
s_shar |
3 |
280 |
29 мар 2017, 22:09 |
|
Найти момент инерции
в форуме Интегральное исчисление |
pukimon |
1 |
245 |
29 май 2016, 13:11 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Yandex [bot] и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Условие задачи:
Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового шара массой 1 кг об очень тяжелую стенку, движущуюся со скоростью 5 см/с. Шар до удара двигался не вращаясь перпендикулярно стенке, навстречу ей со скоростью 10 см/с.
Задача №2.10.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(m=1) кг, (u=5) см/с, (upsilon=10) см/с, (M gg m), (Q-?)
Решение задачи:
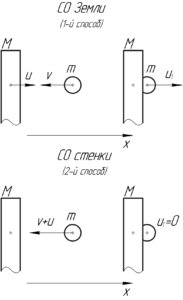
Первый способ. Запишем закон сохранения импульса в проекции на ось (x) и закон сохранения энергии для системы тел «шар — стенка» в системе отсчета (СО) Земли. Замечу, что этот способ достаточно трудоёмкий, по сравнению со вторым.
Из равенства (1) выразим скорость стенки с шаром (u_1) после удара:
Полученное выражение для скорости (u_1) подставим в (2).
Оставим искомое количество теплоты (Q) в одной стороне, все остальные члены перенесем в другую, где приведем их под общий знаменатель.
Раскроем в числителе скобки и квадрат разности:
Вынесем в числителе общий множитель (mM) за скобки:
Воспользуемся основным свойством дроби и поделим и числитель и знаменатель на (M).
Так как по условию стенка очень тяжелая, то есть (M gg m), то отношение (<frac>) стремится к нулю, значит им можно пренебречь. В итоге конечная формула такая:
Второй способ. Перейдем в систему отсчета (СО), связанную с массивной стенкой. В этой СО скорость свинцового шарика равна (upsilon + u) и направлена к стенке. После удара скорость шарика станет такой же, как и у стенки, то есть в этой СО станет равной нулю. Получается, что вся кинетическая энергия шарика в этой СО перейдет в теплоту:
Как Вы видите, второй способ решения этой задачи существенно короче.
Переведем скорости в систему СИ, а уже потом будет считать ответ:
Ответ: 11,25 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Вследствие изменения полной механической энергии системы может выделяться теплота.
Наличие сил трения (сопротивления) между телами замкнутой системы приводит к выделению энергии в виде теплоты:
где E 1 — полная механическая энергия системы в начальном состоянии; E 2 — полная механическая энергия системы в конечном состоянии.
Если теплота в механической системе выделяется в результате совершения работы силами трения, то количество выделившейся при этом теплоты может быть рассчитано по формуле
где A тр — работа, совершенная силами трения.
Превращение части механической энергии в теплоту происходит при абсолютно неупругом столкновении (ударе) двух и более тел.
Абсолютно неупругий удар — это столкновение тел, в результате которого тела объединяются и продолжают двигаться как единое целое.
Для абсолютно неупругого удара двух тел:
- выполняется закон сохранения импульса:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ;
- не выполняется закон сохранения полной механической (кинетической) энергии:
m 1 v 1 2 2 + m 2 v 2 2 2 ≠ ( m 1 + m 2 ) u 2 2 ,
где m 1 и m 2 — массы соударяющихся тел; v → 1 и v → 2 — скорости тел до столкновения; ( m 1 + m 2 ) — масса тела, образовавшегося в результате удара; u → — скорость тела, образовавшегося в результате удара.
Разность энергий до и после столкновения равна теплоте, выделившейся в процессе столкновения:
Q = m 1 v 1 2 2 + m 2 v 2 2 2 − ( m 1 + m 2 ) u 2 2 .
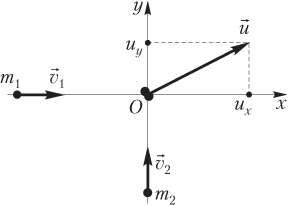
Пример 36. Какая доля энергии двух движущихся с равными по модулю скоростями тел, направленными под прямым углом друг к другу, перейдет в теплоту при абсолютно неупругом ударе? Массы тел относятся как 1:2.
Решение. На рисунке показаны два положения системы тел: до удара и сразу после удара. До удара тела движутся: первое — в положительном направлении оси Ox , второе — в положительном направлении оси Oy . Столкновение тел (абсолютно неупругий удар) происходит в начале системы координат. В результате абсолютно неупругого удара тела объединяются и движутся как единое целое со скоростью u → .
Полная механическая энергия системы является кинетической энергией:
E 1 = W k 1 + W k 2 ;
где W k 1 = m 1 v 1 2 2 — кинетическая энергия первого тела до удара; W k 2 = m 2 v 2 2 2 — кинетическая энергия второго тела до удара; m 1 — масса первого тела; m 2 — масса второго тела; v 1 — модуль скорости первого тела до удара; v 2 — модуль скорости второго тела до удара; W k = ( m 1 + m 2 ) u 2 2 — кинетическая энергия объединенного тела после удара; ( m 1 + m 2 ) — масса объединенного тела после удара; u — модуль скорости объединенного тела после удара.
Теплота, выделившаяся в результате абсолютно неупругого удара, определяется разностью полных механических энергий системы до удара и после него:
Для ее вычисления необходимо определить скорость объединенного тела.
Воспользуемся законом сохранения импульса, записав его в виде:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
или в проекциях на координатные оси,
O x : m 1 v 1 = ( m 1 + m 2 ) u x ; O y : m 2 v 2 = ( m 1 + m 2 ) u y . >
Выразим отсюда проекции скорости объединенного тела:
u x = m 1 v 1 m 1 + m 2 u y = m 2 v 2 m 1 + m 2 >
и подставим их в формулу, определяющую квадрат скорости объединенного тела:
u 2 = u x 2 + u y 2 = ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 .
Полная механическая энергия объединенного тела, таким образом, определяется формулой
E 2 = ( m 1 + m 2 ) u 2 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] .
- равенства модулей скоростей тел до удара:
- соотношения между массами тел:
запишем полные механические энергии системы:
E 1 = m 1 v 1 2 2 + m 2 v 2 2 2 = m v 2 2 + 2 m v 2 2 = 3 2 m v 2 ;
E 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] = 5 6 m v 2 .
Количество теплоты, выделившейся после абсолютно неупругого удара, определяется формулой
Q = E 1 − E 2 = 3 2 m v 2 − 5 6 m v 2 = 2 3 m v 2 .
Доля механической энергии, превратившейся в теплоту в результате абсолютно неупругого удара,
η = Q E 1 = 2 m v 2 3 2 3 m v 2 = 4 9 ≈ 0,44 .
При абсолютно неупругом ударе двух тел с заданными соотношениями масс и скоростей в теплоту перешло около 44 % механической энергии системы.
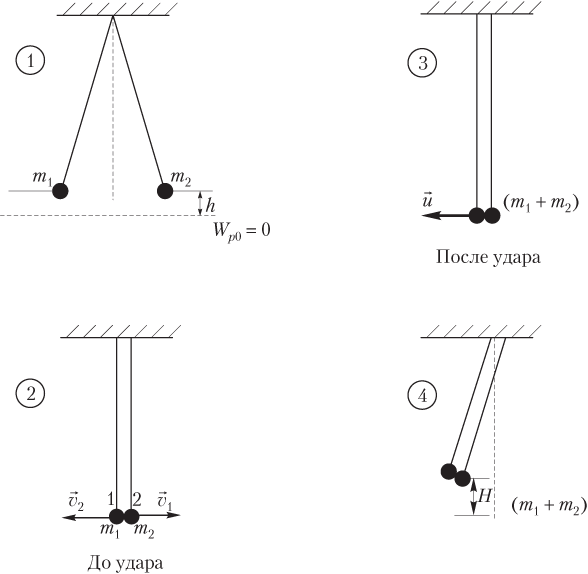
Пример 37. Два пластилиновых шарика, массы которых соотносятся как 1:5, подвешены на нитях одинаковой длины. Шарики симметрично разводят в противоположные стороны и отпускают. Какая часть механической энергии перейдет в теплоту при абсолютно неупругом ударе?
Решение. На рисунке показаны четыре состояния системы тел:
1) шарики симметрично разведены в стороны, при этом они подняты на высоту h над нулевым уровнем потенциальной энергии; полная механическая энергия системы является потенциальной:
E 1 = m 1 gh + m 2 gh ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где g — модуль ускорения свободного падения; h — первоначальная высота шариков над нулевым уровнем потенциальной энергии;
2) шарики подлетают друг к другу (но соударения еще не происходит); полная механическая энергия системы является кинетической:
E 2 = m 1 v 1 2 2 + m 2 v 2 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
E 2 = m 2 ( v 1 2 + 5 v 2 2 ) ,
где v 1 — модуль скорости первого шарика; v 2 — модуль скорости второго шарика;
3) шарики после абсолютно неупругого удара объединяются и движутся как единое целое с некоторой скоростью; полная механическая энергия системы является кинетической:
E 3 = ( m 1 + m 2 ) u 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где u — модуль скорости объединенного тела непосредственно после удара;
4) объединенное тело поднимается на некоторую высоту, полная механическая энергия системы является потенциальной:
E 4 = ( m 1 + m 2 ) gH ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где H — максимальная высота, на которую может подняться объединенное тело.
При переходе системы из первого состояния во второе полная механическая энергия сохраняется как для всей системы, так и для каждого шарика в отдельности:
m 1 g h = m 1 v 1 2 2 ; m 2 g h = m 2 v 2 2 2 . >
Отсюда следует равенство модулей скоростей шариков перед абсолютно неупругим ударом:
v = v 1 = v 2 = 2 g h .
С учетом этого равенства полная механическая энергия системы перед ударом определяется формулой
При переходе системы из второго состояния в третье полная механическая энергия системы не сохраняется (при абсолютно неупругом ударе часть энергии переходит в теплоту), однако импульс системы сохраняется:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
в проекции на направление скорости объединенного тела
− m 1 v 1 + m 2 v 2 = ( m 1 + m 2 ) u ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ) и равенства модулей скоростей ( v = v 1 = v 2 ):
Отсюда найдем отношение модулей скоростей шариков до и после удара:
Искомой величиной является доля механической энергии, которая перейдет в результате абсолютно неупругого удара в теплоту, т.е.
η = Q E 2 = E 2 − E 3 E 2 = 1 − E 3 E 2 ,
где E 2 — полная механическая энергия системы до удара (состояние 2); E 3 — полная механическая энергия системы после удара (состояние 3).
Подстановка в формулу соответствующих энергий и отношения скоростей ( u / v ) дает искомую долю:
η = 1 − 3 m u 2 3 m v 2 = 1 − u 2 v 2 = 1 − ( u v ) 2 = 1 − ( 2 3 ) 2 = 5 9 ≈ 0,56 .
Таким образом, при абсолютно неупругом ударе шариков с заданным соотношением масс в теплоту превращается около 56 % их суммарной механической энергии.
Пример 38. Тело массой 2,0 кг влетает в вязкую среду со скоростью 10 м/c. Определить кинетическую энергию тела при вылете из среды, если 30 % его механической энергии в среде превращается в теплоту.
Решение. На рисунке показаны два положения тела:
1) перед попаданием в вязкую среду; тело имеет полную механическую (кинетическую) энергию E 1 ;
2) после вылета из вязкой среды; тело имеет полную механическую (кинетическую) энергию E 2 .
Теплота, которая выделяется при движении тела в вязкой среде, определяется разностью
где Q = 0,3 E 1 — по условию задачи.
Выразим искомую кинетическую энергию тела при вылете из вязкой среды:
Замена Q = 0,3 E 1 преобразует формулу к виду:
E 2 = E 1 − 0,3 E 1 = 0,7 E 1 ,
где E 1 = m v 1 2 2 — кинетическая энергия тела перед его попаданием в вязкую среду; m — масса тела; v 1 — модуль первоначальной скорости тела.
Окончательная формула для расчета искомой кинетической энергии имеет следующий вид:
Скорость брошенного мяча непосредственно перед ударом об абсолютно гладкую стену была вдвое больше его скорости сразу после удара. Какое количество теплоты выделилось при ударе, если перед ударом кинетическая энергия мяча была равна 20 Дж? (Ответ дайте в джоулях.)
Кинетическая энергия пропорциональна квадрату скорости. Поскольку скорость после удара уменьшилась в 2 раза, кинетическая энергия мяча уменьшилась в 4 раза и стала равна 5 Дж. По закону сохранения, количество теплоты, выделившееся после удара равняется убыли кинетической энергии:
Для приведенного здесь решения задачи существенно, что стенка, о которую ударяется мяч, абсолютно гладкая. Действительно, в противном случае на мяч во время удара может дейстовать еще и сила трения со стороны стенки, которая приведет к тому, что мяч после удара будет вращаться поэтому кинетическая энергия шара после удара будет состоять из энергии поступательного и вращательного движений. Следовательно, судить о величине выделившегося тепла будет невозможно.