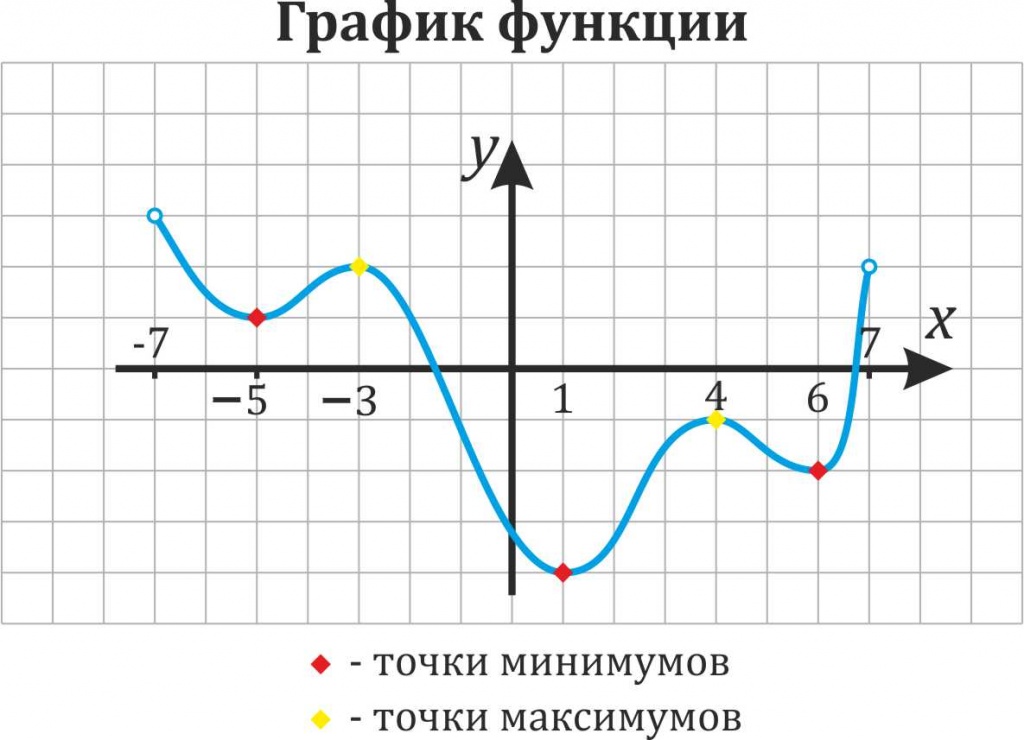
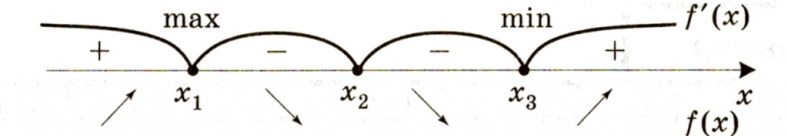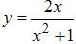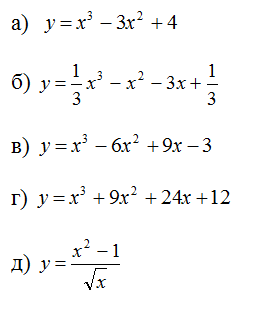Как найти количество точек экстремума по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

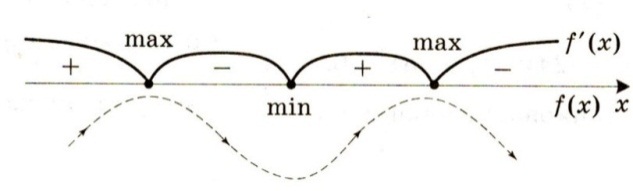
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

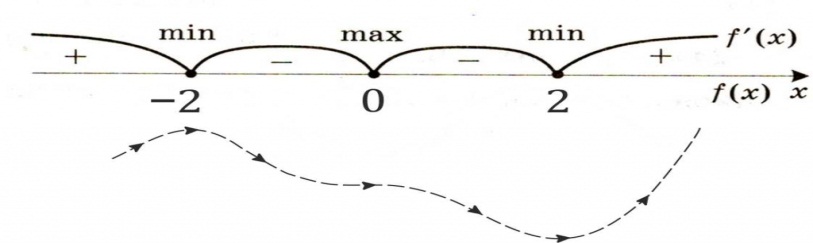
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Экстремумы функции: признаки существования, примеры решений

Экстремумы функции, их необходимый и достаточный признаки

Точка экстремума функции — это точка области определения функции, в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции.

Нахождение эктремумов функции может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графиков. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций. И ещё потребуются таблица производных простых функций и таблица производных сложных функций (откроются в новом окне), так как в примерах указано, какая именно табличная производная найдена.

Рассмотрим график непрерывной функции (рисунок снизу).

Определение. Точка x 1 области определения функции f(x) называется точкой максимума функции, если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) > f(x 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 1 максимум.

Определение. Точка x 2 области определения функции f(x) называется точкой минимума функции, если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 2 минимум.

Допустим, точка x 1 — точка максимума функции f(x) . Тогда в интервале до x 1 функция возрастает, поэтому производная функции больше нуля ( f ‘(x) > 0 ), а в интервале после x 1 функция убывает, следовательно, и производная функции меньше нуля ( f ‘(x) ). Тогда в точке x 1 производная функции равна нулю или не существует.

Допустим также, что точка x 2 — точка минимума функции f(x) . Тогда в интервале до x 2 функция убывает, а производная функции меньше нуля ( f ‘(x) ), а в интервале после x 2 функция возрастает, а производная функции больше нуля ( f ‘(x) > 0 ). В этом случае также в точке x 2 производная функции равна нулю или не существует.

Теорема Ферма (необходимый признак существования экстремума функции). Если точка x 0 — точка экстремума функции f(x) , то в этой точке производная функции равна нулю ( f ‘(x) = 0 ) или не существует.

Определение. Точки, в которых производная функции равна нулю или не существует, называются критическими точками.

Пример 1. Рассмотрим функцию .

В точке x = 0 производная функции равна нулю, следовательно, точка x = 0 является критической точкой. Однако, как видно на графике функции, она возрастает во всей области определения, поэтому точка x = 0 не является точкой экстремума этой функции.

Таким образом, условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести и другие примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Поэтому нужно располагать достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно — максимум или минимум.

Теорема (первый достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с «плюса» на «минус», то точкой максимума, а если с «минуса» на «плюс», то точкой минимума.

Если же вблизи точки x 0 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки x 0 . В этом случае в точке x 0 экстремума нет.

Итак, чтобы определить точки экстремума функции, требуется выполнить следующее:

Найти производную функции.
Приравнять производную нулю и определить критические точки.
Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с «плюса» на «минус», то критическая точка является точкой максимума, а если с «минуса» на «плюс», то точкой минимума.
Вычислить значение функции в точках экстремума.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 2. Найти экстремумы функции .

Решение. Найдём производную функции (в таблице производных сложных функций — производная 6):

Приравняем производную нулю, чтобы найти критические точки:

Так как для любых значений «икса» знаменатель не равен нулю, то приравняем нулю числитель:

Получили одну критическую точку x = 3 . Определим знак производной в интервалах, разграниченных этой точкой:

в интервале от минус бесконечности до 3 — знак минус, то есть функция убывает,

в интервале от 3 до плюс бесконечности — знак плюс, то есть функция возрастает.

То есть, точка x = 3 является точкой минимума.

Найдём значение функции в точке минимума:

Таким образом, точка экстремума функции найдена: (3; 0) , причём она является точкой минимума.

Теорема (второй достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если вторая производная функции в этой точке не равна нулю ( f »(x) ≠ 0 ), причём, если вторая производная больше нуля ( f »(x) > 0 ), то точкой максимума, а если вторая производная меньше нуля ( f »(x) ), то точкой минимума.

Замечание 1. Если в точке x 0 обращаются в нуль и первая, и вторая производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума функции.

Замечание 2. Второй достаточный признак экстремума функции неприменим и тогда, когда в стационарной точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно вопользоваться первым достаточным признаком экстремума функции.

Локальный характер экстремумов функции

Из приведённых определений следует, что экстремум функции имеет локальный характер — это наибольшее и наименьшее значение функции по сравнению с близлежайшими значениями.

Предположим, вы рассматриваете свои заработки в отрезке времени протяжённостью в один год. Если в мае вы заработали 45 000 рублей, а в апреле 42 000 рублей и в июне 39 000 рублей, то майский заработок — максимум функции заработка по сравнению с близлежайшими значениями. Но в октябре вы заработали 71 000 рублей, в сентябре 75 000 рублей, а в ноябре 74 000 рублей, поэтому октябрьский заработок — минимум функции заработка по сравнению с близлежашими значениями. И вы легко видите, что максимум среди значений апреля-мая-июня меньше минимума сентября-октября-ноября.

Говоря обобщённо, на промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо максимума. Так, для функции изображённой на рисунке выше, .

То есть не следует думать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на всём рассматриваемом отрезке. В точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума — наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.

Поэтому можно уточнить приведённое выше понятие точек экстремума функции и называть точки минимума точками локального минимума, а точки максимума — точками локального максимума.

Ищем экстремумы функции вместе

Пример 3. Найти экстремумы функции и построить её график.

Решение. Функция определена и непрерывна на всей числовой прямой. Её производная (и первое, и второе слагаемые — табличная производная 3) существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых , т.е. , откуда и . Критическими точками и разбивают всю область определения функции на три интервала монотонности: . Выберем в каждой из них по одной контрольной точке и найдём знак производной в этой точке.

Для интервала контрольной точкой может служить : находим . Взяв в интервале точку , получим , а взяв в интервале точку , имеем . Итак, в интервалах и , а в интервале . Согласно первому достаточному признаку экстремума, в точке экстремума нет (так как производная сохраняет знак в интервале ), а в точке функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: , а . В интервале функция убывает, так как в этом интервале , а в интервале возрастает, так как в этом интервале .

Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При получим уравнение , корни которого и , т. е. найдены две точки (0; 0) и (4; 0) графика функции. Используя все полученные сведения, строим график (см. в начале примера).

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти экстремумы функции и построить её график.

Областью определения функции является вся числовая прямая, кроме точки , т.е. .

Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала .

Находим производную (каждое слагаемое находим как табличную производную 3) и критические точки функции:

1) ;

2) ,

но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.

Таким образом, заданная функция имеет две критические точки: и . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку . Для этого найдём вторую производную и определим её знак при : получим . Так как и , то является точкой минимума функции, при этом .

Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:

(здесь символом обозначено стремление x к нулю справа, причём x остаётся положительным; аналогично означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если , то . Далее, находим

т.е. если , то .

Точек пересечения с осями график функции не имеет. Рисунок — в начале примера.

Найти экстремумы функции самостоятельно, а затем посмотреть решение

Пример 5. Найти экстремумы функции .

Пример 6. Найти экстремумы функции .

Пример 7. Найти экстремумы функции .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Продолжаем искать экстремумы функции вместе

Пример 8. Найти экстремумы функции .

Решение. Найдём область определения функции. Так как должно выполняться неравенство , то из получаем .

Найдём первую производную функции (производная вида 2 в таблице производных сложной функции):

Найдём критические точки функции:

Точки и не могут быть точками экстремума, так как находятся на границе области определения функции. В точке производная функции меняет знак с плюса на минус, а в точке — с минуса на плюс. Следовательно, — точка максимума, а точка — точка минимума функции.

Найдём значения функции в этих точках:

Таким образом, экстремумы функции:

Пример 9. Найти экстремумы функции .

Решение. Найдём область определения функции.

Найдём критические точки функции:

Таким образом, у данной функции две критические точки: и . Определим значения производной в критических точках. При переходе через точку производная функции продолжает убывать (сохраняет знак минус), а при переходе через точку — начинает возрастать (меняет знак с минуса на плюс). Следовательно, — точка минимума функции.

Найдём значение функции в точке минимума:

Таким образом, минимум функции:

Пример 10. Найти экстремумы функции .

Решение. Найдём первую производную функции (первое слагаемое — производная вида 12 в таблице производных простых функций, второе — производная вида 6 в таблице производных сложной функции):

Найдём критические точки функции:

Так как для любого действительного x должно выполняться условие , то

Таким образом, данная функция имеет одну критическую точку. Определим значения производной в критической точке. При переходе через точку производная функции начинает убывать (меняет знак с плюса на минус). Следовательно, — точка максимума функции.

Найдём значение функции в точке максимума:

Таким образом, максимум функции:

источники:

http://cos-cos.ru/math/327/

http://function-x.ru/function_extremum.html

Источник

Тема: Максимумы, минимумы функций

1. Изучить весь предложенный теоритический материал по данной теме и записать в тетрадь.

2. Рассмотреть пример 1,2 и записать в тетрадь.

3. Решить самостоятельно в тетради (отправить мне на эл. почту) – за третий пункт будет выставлена оценка!

1. Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

2. Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике ниже, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. y. Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке ниже, −5 точка минимума, а 1 – минимум (или экстремум — смотрим по ОУ).

3. Как найти точки экстремумов функции по графику производной?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производной — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки −13, −11, −9,−7 и 3. Количество точек экстремума функции 5.

4. Как найти точки максимумов или минимумов функции по графику производной)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди −13, −11, −9,−7 и 3.

Начнем с−13: до −13 производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что −13 – точка максимума.

−11: производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что −11 – это минимум.

−9: функция возрастает, а потом убывает – максимум.

−7: минимум.

3: максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. — Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции?

Найдите производную функции f′(x).
Найдите корни уравнения f′(x)=0.
Нарисуйте ось x и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью f′(x), а под осью f(x).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: — если f′(x) изменила знак с «+» на «−», то x1 – точка максимума; — если f′(x) изменила знак с «−» на «+», то x3 – точка минимума; — если f′(x) не изменила знак, то x2 – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

2.Рассмотрим примеры:

Пример 1.

Найдите точку максимума функции y=3x⁵−20x³−54. Решение:

1.Найдем производную функции: y′=15x⁴−60x². 2. Приравняем её к нулю и решим уравнение:

15x⁴−60x²=0 |:15 x⁴−4x²=0 x²(x²−4)=0 x=0 x²−4=0 x=±2

3. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является −2.

Ответ. −2.

Пример 2.

Найдите точку максимума функции

Решение 1. Найдём производную (по правилу производная дроби) и приравниваем её к нулю:

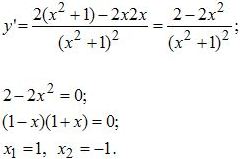
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.

Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.

3. Исследовать на экстремумы функцию (самостоятельно):

КРИТЕРИИ «5» — все 5 функций

«4» — 3,4 функции

«3» — 2 функции

Решение 3 пункта записываете в тетрадь и предоставляете для проверки, оценка выставляется в ГИС

Источник

Рассмотрим задания, в которых требуется найти для функции точки максимума на графике производной.

Важно внимательно читать условие. Точки минимума и максимума функции на графике функции находим иначе!

№1

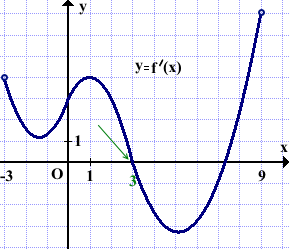
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-3;9 ). Найти точку максимума функции f(x).

Решение:

В точке максимума производная непрерывной функции обращается в нуль и при переходе через точку максимума знак производной меняется с плюса на минус.

Соответственно, график производной в точке максимума пересекает ось абсцисс сверху вниз.

В данном случае точкой максимума функции f(x) является точка с абсциссой x=3.

Ответ: 3.

№2

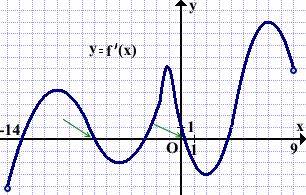
На рисунке изображён график функции y=f'(x), определённой на интервале (-14;9). Определить количество точек максимума функции f(x).

Решение:

В точках максимума производная меняет свой знак с плюса на минус.

График производной при переходе через точку максимума пересекает ось абсцисс сверху вниз.

График производной y=f'(x) данной функции пересекает ось Ox в двух точках. Значит, функция f(x) имеет две точки максимума.

Ответ: 2.

№3

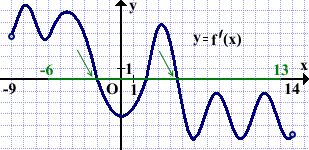
На рисунке изображён график производной функции f(x), определённой на интервале (-9;14). Найти количество точек максимума функции f(x) на отрезке [-6;13].

Решение:

Выделяем рассматриваемый отрезок [-6;13].

В точках максимума функции f(x) график её производной f'(x) пересекает ось Ox сверху вниз.

На отрезке [-6;13] график производной данной функции пересекает ось абсцисс в двух точках. Следовательно, на этом отрезке функция f(x) имеет две точки максимума.

Ответ: 2.

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 21 1–20 | 21–21

Добавить в вариант

На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y  =  12 или совпадает с ней.

На рисунке изображен график производной функции f(x), определенной на интервале (−15; 2). Найдите количество точек максимума функции f(x) на отрезке [−11;0].

На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].

На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y  =  6 или совпадает с ней.

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,2 кг никеля. Во второй области для добычи х кг алюминия в день требуется человеко-часов труда, а для добычи y кг никеля в день требуется человеко-часов труда.

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.

В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется человеко-часов труда, а для добычи у кг никеля в день требуется человеко-часов труда.

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.

В двух областях работают по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,3 кг никеля. Во второй области для добычи x кг алюминия в день требуется x² человеко-часов труда, а для добычи у кг никеля в день требуется y² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую суммарную массу металлов можно добыть в двух областях за сутки?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.

На каждом из двух заводов работает по 100 человек. На первом заводе один рабочий изготавливает за смену 3 детали А или 1 деталь В. На втором заводе для изготовления t деталей (и А, и В) требуется t² человеко-смен. Оба завода поставляют детали на комбинат, где собирают изделие, причем для его изготовления нужна 1 деталь А и 3 детали В. При этом заводы договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.

Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара.

За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе,  — 300 рублей.

Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

На рисунке изображен график y  =  f ‘(x)  — производной функции f(x), определенной на интервале (−17; 5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−15; 0].

На рисунке изображен график y  =  f ‘(x)  — производной функции f(x), определенной на интервале (−12; 11). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−8; 9].

На доске написано N различных натуральных чисел, каждое из которых не превосходит 99. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b – a, и ни одно из написанных чисел не является делителем числа b – a.

а)  Могли ли на доске быть написаны какие-то два числа из чисел 18, 19 и 20?

б)  Среди написанных на доске чисел есть 17. Может ли N быть равно 25?

в)  Найдите наибольшее значение N.

Всего: 21 1–20 | 21–21

Источник