Всего: 23 1–20 | 21–23
Добавить в вариант
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −x − 12 или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x − 19 или совпадает с ней.
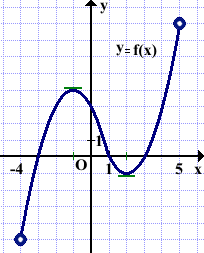
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
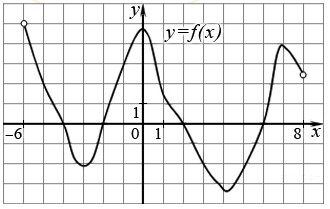
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −6.
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −6.
На рисунке изображён график функции y = f(x), определённой на интервале (−3; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 1.
На рисунке изображён график функции y = f(x), определённой на интервале (−4; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 18.
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 3x или совпадает с ней.
На рисунке изображен график функции y = f(x), определенной на интервале (−9; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −10.
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 6). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −12.
На рисунке изображён график — производной функции
определенной на интервале (−12; 2). Найдите количество точек, в которых касательная к графику функции
параллельна прямой y = 3x − 2 или совпадает с ней.
Всего: 23 1–20 | 21–23
Узнать ещё
Знание — сила. Познавательная информация
Касательная параллельна прямой
Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.
На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.
Теперь рассмотрим аналогичное задание, в котором дан график производной функции.
2)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).
Значит, ищем точки, в которых значение производной равно нулю.
Таких точек три (с абсциссами x=-3, x=1 и x=3).
3)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=3x-11 или совпадает с ней.
Поэтому ищем точки, в которых значение производной равно 3.
Таких точек в данном примере четыре.
4)На рисунке изображён график производной функции f(x). Найти абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=4-x или совпадает с ней.
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки xo=7.
Справочник репетитора по математике. Касательные, экстремумы и исследования функций
by Колпаков А.Н. on 5 января 2011
Cправочник репетитора по математике предназначен для учащихся 5-11 классов и для преподавателей математики. Последние найдут в нем несколько оригинальных подходов к подаче и оформлению теоретических конспектов, упрощающих работу школьников с математическими понятиями и законами.
Касательная к графику функции.
Школьное определение касaтельной: прямая y=f (x) называется касательной к графику функции f (x) в точке 


Строгое определение касательной (из курса математического анализа) : прямая 




Иллюстрация касательной m к графику функции 

Геометрический смысл производной: Значение производной функции 




Комментарий репетитора по математике: угол наклона касательной определяется как направленный положительный угол, то есть тот самый угол, который вы привыкли откладывать на тригонометрическом круге от положительного направления оси OX против часовой стрелки. Поэтому, если если касательная отклонена влево от вертикального положения, ваш угол наклона окажется тупым, то есть принадлежащим промежутку 
Общая форма уравнения касательной: 
Окончательная форма уравнения касательной :
Полезные факты для решения задач на касательную:
1) две наклонный прямые параллельны, тогда и только тогда, когда их угловые коэффициенты равны.
2) две наклонный прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно -1.
Как найти угол наклона касательной по ее угловому коэффициенту:
Если 

Если 
Достаточный признак возрастания функции: если все значения производной некоторой функции положительны внутри промежутка, то функция внутри него строго возрастает.
Замечание репетитора по математике: если концы промежутка являются точками непрерывности функции (один или оба), то их можно присоденить к указанному промежутку возрастания.
Достаточный признак убывания функции: если все значения производной некоторой функции отрицательны внутри промежутка, то функция внутри него строго убывает.
Замечание репетитора по математике: если функция непрерывна на концах промежутка (на одном или на обоих), то эти концы можно присоединить к указанному промежутку убывания.
Блиц вопросы к репетитору:
Что такое критическая точка? Внутренняя точка области определения функции называется критической, если производная в этой точке либо не сущуствует, либо она равна нулю.
Что такое стационарная точка: Если у критической точки производная равна нулю — она называется стационарной точной.
Экстремумы
Минимум функции.
Определение: Точка 






Фрагмент графика функции, имеющей точку минимума:
Комментарий репетитора по математики к рисунку: знаки — и + на оси OХ показывают на отрицательные/положитлеьные значения производной в левой/правой окрестности точки 
Максимум функции.
Определение:Точка 






Фрагмент графика функции, имеющей точку максимума:
Комментарий репетитора по математике: все обозначения и опорные знаки для подачи материала преподавателем аналогичны случаю с минимумом.
Экстремум — общее название минимума и максимума. Точка экстремума — общее название для точки минимума и точки максимума. На всех рисунках 

Необходимое условие существования экстремума: если 

Достаточное условие существования экстремума: если функция y=f (x) непрерывна в точке 


Признак минимума функции: если функция y=f (x) непрерывна в точке 

Признак максимума функции: если функция y=f (x) непрерывна в точке 

Алгоритм нахождения наибольшего и наименьшего значения функции y=f (x) на отрезке [a;b], на которм она непрерывна
1) Найдите производную 
2) Найдите стационарные точки, решив уравнение 
2*) В редких случаях функция может иметь точки, в которых производной не существует. Их тоже нужно выявить.
3) Выберите из всех найденных точек те, которые попадают в исследуемый отрезок
4) Найдите значения данной функции в выбранных точках
5) Выберите среди них наименьшее и наибольшее
План исследования функции с применением производной. Построение графика.
1) Найдите производную 
2) Разложите ее на множители (если это возможно) или приведите все ее дроби к общему знаменателю, а затем разложите числитель. Тем самым вы ее готовите к дальнейшему исследованию методом интервалов
2) Определите у функции критические и стационарные точки, приравнивая числитель и знаменатель ее производной к нулю
2*) Точки, в которых производной не существует (обычно это нули знаменателя) отесите в группу тех, в которых функция будет иметь вертикальные асимптоты
3) Отметьте все найденные точки на оси Х и раставьте методом интервалов на образовавшихся промежутках знаки производной
4) Определите промежутки монотонности (промежутки возрастания и убывания) и над каждым из них поставьте соответствующую стрелку в соответствии с видом этой монотонности
5) Определите через признак минимума и максимума (или по характеру расположения стрелок) соответствующие точки экстремумов и найдите значения функции в этих точках
6) Нанесите их на координатной плоскости и также по характеру стрелок проведите через эти точки график.
Замечание репетитора по математике: аккуратнее выполняйте рисунок вблизи асимптот. График функции не должен их пересекать и обрываться рядом с ними. Плавно приближайте его к асимтоте пока на это хватает выделенного пространства системы координат.
Удачи в изучении математики!
Колпаков Александр Николаевич, репетитор по математике, Москва, Строгино.
Виртуальный математический справочник профессионального репетитора — преподавателя.
Задание №6. Производная. Поведение функции. Первообразная — профильный ЕГЭ по Математике
Необходимая теория:
Задание 6 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке
Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .
Достроив до прямоугольного треугольника АВС, получим:
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой в точке
При значения выражений и равны.
При этом производная функции равна угловому коэффициенту касательной, то есть .
Из второго уравнения находим или Первому уравнению удовлетворяет только .
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени получим:
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция возрастает.
Если , то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает |
| 0 | 0 |
5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.
Производная функции в точках максимума и минимума функции Таких точек на графике 5.
6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
Функция для которой является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
http://ankolpakov.ru/2011/01/05/spravochnik-repetitora-po-matematike-kasatelnye-ekstremumy-i-issledovaniya-funkcij/
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-7-profilnogo-ege-po-matematike-proizvodnaya-povedenie-funkcii-pervoobraznaya/
Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Решение:
Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.
На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.
Ответ: 2.
Теперь рассмотрим аналогичное задание, в котором дан график производной функции.
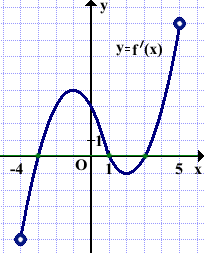
Решение:
Прямые y=k1x+b1 y=k2x+b2 параллельны, если их угловые коэффициенты равны: k1=k2.
y=12=0x+12, ⇒k1=0.
Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).
Значит, ищем точки, в которых значение производной равно нулю.
Таких точек три (с абсциссами x=-3, x=1 и x=3).
Ответ: 3.
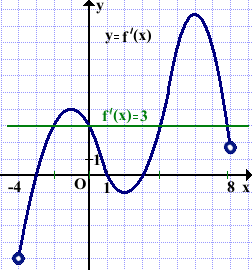
Решение:
y=3x-12, ⇒k1=3.
Прямые параллельны, если k1=k2.
k2=f'(xo).
Поэтому ищем точки, в которых значение производной равно 3.
Таких точек в данном примере четыре.
Ответ: 4.
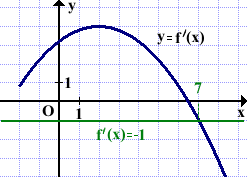
Решение:
y=4-x,⇒k1=-1.
Прямые параллельны, если k1=k2.
Прямые параллельны, если k1=k2.
k2=f'(xo).
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки xo=7.
Ответ: 7.
Задание
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-9;8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x-7 или совпадает с ней?
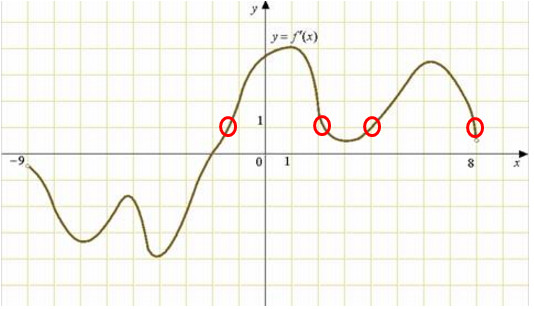
Решение
- Обратим внимание на то, что на рисунке изображен график производной функции.
- Производная функции в точке касания равна угловому коэффициенту касательной.
- Угловой коэффициент прямой – это коэффициент, который стоит перед х, если уравнение прямой записать в виде y = kx + b, то k – угловой коэффициент.
- У параллельных прямых угловые коэффициенты равны.
- Из всего выше сказанного, делаем вывод, что нам необходимо посчитать точки, в которых производная функции равна угловому коэффициенту касательной, а именно 1 (угловой коэффициент касательной равен 1).
- То есть, мы считаем точки, в которых у = 1, так как значение производной функции смотрим по оси у (данные точки выделены красным)
- Получили 4 точки, в которых касательная к графику функции параллельна прямой у = х – 7.
Ответ: 4
Исследование функции с помощью производной. В этой статье мы с вами разберём некоторые задачи связанные с исследованием графика функции. В таких задачах, даётся график функции y = f (x) и ставятся вопросы, связанные с определением количества точек, в которых производная функции положительна (либо отрицательна), а также другие. Их относят к заданиям на применение производной к исследованию функций.
Решение таких задач, и вообще задач связанных с исследованием, возможно только при полном понимании свойств производной для исследования графиков функций и геометрического смысла производной. Поэтому настоятельно рекомендую вам изучить соответствующую теорию. Можете изучить статью на блоге, а также посмотреть справочник (но в нём краткое изложение).
Задачи, где дан график производной мы будем также рассматривать в будущих статьях, не пропустите! Итак, задачи:
На рисунке изображен график функции у = f (х), определенной на интервале (−6; 8). Определите:
1. Количество целых точек, в которых производная функции отрицательна;
2. Количество точек, в которых касательная к графику функции параллельна прямой у = 2;
3. Количество точек, в которых производная равна нулю;
1. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (−6; –3), (0; 4,2), (6,9; 8). В них содержатся целые точки −5, −4, 1, 2, 3, 4, и 7. Получили 7 точек.
2. Прямая y = 2 параллельная оси ох. Касательная будет параллельна прямой y = 2 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот). Таких точек четыре: –3; 0; 4,2; 6,9
3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Определите количество целых точек, в которых производная функции положительна.
Посмотреть решение.
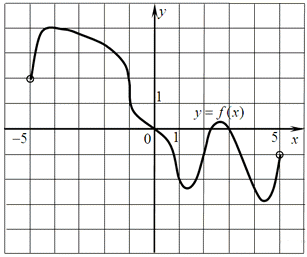
На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите:
1. Количество целых точек, в которых производная функции положительна;
2. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 3;
3. Количество точек, в которых производная равна нулю;
1. Из свойств производной функции известно, что она положительна на интервалах, на которых функция возрастает, т. е. на интервалах (1,4; 2,5) и (4,4;5). В них содержится только одна целая точка х = 2.
2. Прямая y = 3 параллельная оси ох. Касательная будет параллельна прямой y = 3 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот).
Таких точек четыре: –4,3; 1,4; 2,5; 4,4
3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Определите количество целых точек, в которых производная функции f (x) отрицательна.
Посмотреть решение.
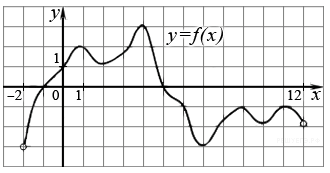
На рисунке изображен график функции у = f (х), определенной на интервале (−2; 12). Найдите:
1. Количество целых точек, в которых производная функции положительна;
2. Количество целых точек, в которых производная функции отрицательна;
3. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 2;
4. Количество точек, в которых производная равна нулю.
1. Из свойств производной функции известно, что она положительна на интервалах, на которых функция возрастает, т. е. на интервалах (–2; 1), (2;4), (7; 9) и (10;11). В них содержатся целые точки: –1, 0, 3, 8. Всего их четыре.
2. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (1; 2), (4; 7), (9; 10), (11;12). В них содержатся целые точки 5 и 6. Получили 2 точки.
3. Прямая y = 2 параллельная оси ох. Касательная будет параллельна прямой y = 2 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот). Таких точек семь: 1; 2; 4; 7; 9; 10; 11.
4. Производная равна нулю в семи точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Найдите сумму точек экстремумов функции f (x). Посмотреть решение.
Как видите, ничего сложного нет. Желаю вам успехов!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.