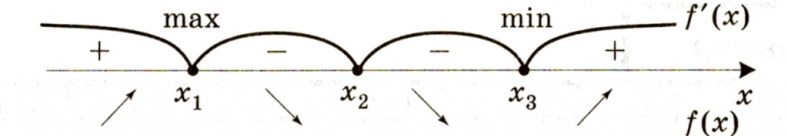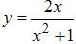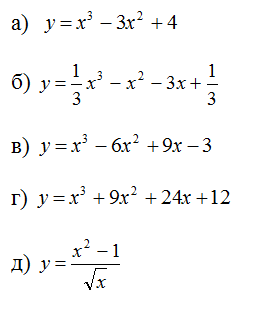Как найти количество точек максимума производной функции

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

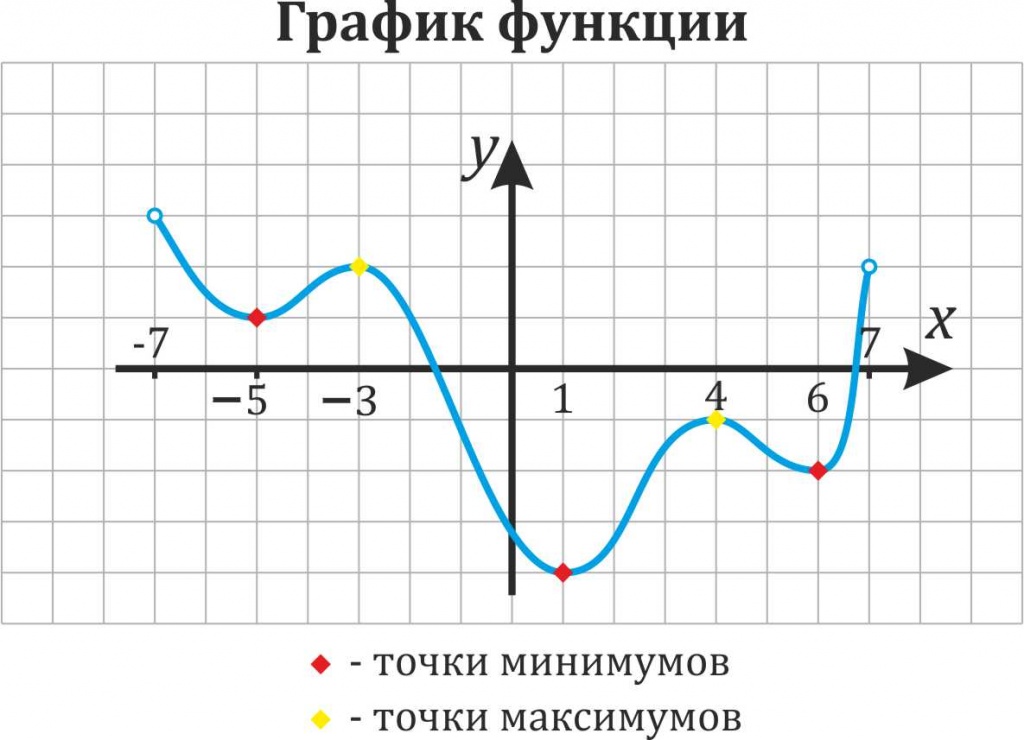
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)). 
2. Найдите корни уравнения (f'(x)=0). 
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов). 
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью). 
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   — если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   — если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   — если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

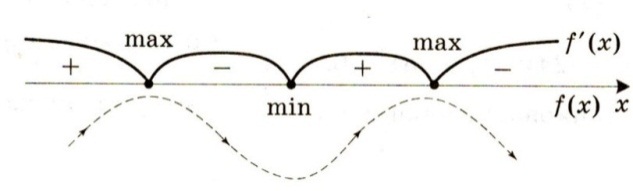
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0)      (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0)       (x^2-4=0)
               (x=±2)

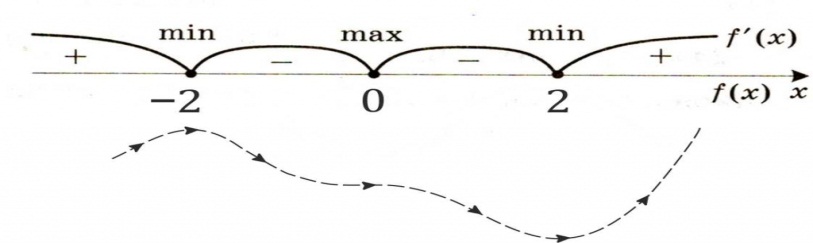
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Рассмотрим задания, в которых требуется найти для функции точки максимума на графике производной.

Важно внимательно читать условие. Точки минимума и максимума функции на графике функции находим иначе!

№1

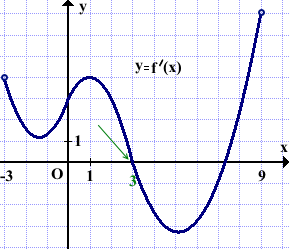
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-3;9 ). Найти точку максимума функции f(x).

Решение:

В точке максимума производная непрерывной функции обращается в нуль и при переходе через точку максимума знак производной меняется с плюса на минус.

Соответственно, график производной в точке максимума пересекает ось абсцисс сверху вниз.

В данном случае точкой максимума функции f(x) является точка с абсциссой x=3.

Ответ: 3.

№2

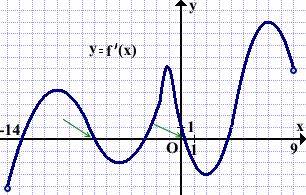
На рисунке изображён график функции y=f'(x), определённой на интервале (-14;9). Определить количество точек максимума функции f(x).

Решение:

В точках максимума производная меняет свой знак с плюса на минус.

График производной при переходе через точку максимума пересекает ось абсцисс сверху вниз.

График производной y=f'(x) данной функции пересекает ось Ox в двух точках. Значит, функция f(x) имеет две точки максимума.

Ответ: 2.

№3

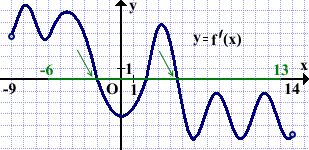
На рисунке изображён график производной функции f(x), определённой на интервале (-9;14). Найти количество точек максимума функции f(x) на отрезке [-6;13].

Решение:

Выделяем рассматриваемый отрезок [-6;13].

В точках максимума функции f(x) график её производной f'(x) пересекает ось Ox сверху вниз.

На отрезке [-6;13] график производной данной функции пересекает ось абсцисс в двух точках. Следовательно, на этом отрезке функция f(x) имеет две точки максимума.

Ответ: 2.

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 21    1–20 | 21–21

Добавить в вариант

Всего: 21    1–20 | 21–21

Тема: Максимумы, минимумы функций

1. Изучить весь предложенный теоритический материал по данной теме и записать в тетрадь.

2. Рассмотреть пример 1,2 и записать в тетрадь.

3. Решить самостоятельно в тетради (отправить мне на эл. почту) – за третий пункт будет выставлена оценка!

1. Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

2. Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике ниже, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. y. Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке ниже, −5 точка минимума, а 1 – минимум (или экстремум — смотрим по ОУ).

3. Как найти точки экстремумов функции по графику производной?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производной — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки −13, −11, −9,−7 и 3. Количество точек экстремума функции 5.

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось x).

4. Как найти точки максимумов или минимумов функции по графику производной)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди −13, −11, −9,−7 и 3.

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с−13: до −13 производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что −13 – точка максимума.

−11: производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что −11 – это минимум.

−9: функция возрастает, а потом убывает – максимум.

−7: минимум.

3: максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. — Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции f′(x).
2. Найдите корни уравнения f′(x)=0.
3. Нарисуйте ось x и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью f′(x), а под осью f(x).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: — если f′(x) изменила знак с «+» на «−», то x1 – точка максимума; — если f′(x) изменила знак с «−» на «+», то x3 – точка минимума; — если f′(x) не изменила знак, то x2 – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

2.Рассмотрим примеры:

Пример 1.

Найдите точку максимума функции y=3x⁵−20x³−54. Решение:

1.Найдем производную функции: y′=15x⁴−60x². 2. Приравняем её к нулю и решим уравнение:

15x⁴−60x²=0 |:15 x⁴−4x²=0 x²(x²−4)=0 x=0 x²−4=0 x=±2

3. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является −2.

Ответ. −2.

Пример 2.

Найдите точку максимума функции

Решение 1. Найдём производную (по правилу производная дроби) и приравниваем её к нулю:

Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.

Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.

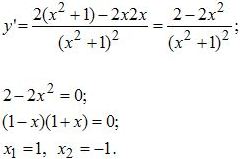
3. Исследовать на экстремумы функцию (самостоятельно):

КРИТЕРИИ «5» — все 5 функций

«4» — 3,4 функции

«3» — 2 функции

Решение 3 пункта записываете в тетрадь и предоставляете для проверки, оценка выставляется в ГИС

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.