Материал из Algocode wiki
Перейти к: навигация, поиск
Тяжелые и легкие вершины
Назовем $textit{тяжелой}$ вершину, имеющую более $sqrt{E}$ соседей. Все оставшиеся вершины назовем $textit{легкими}$.
Утверждение:
В графе не более $2 cdot sqrt{E}$ тяжелых вершин.
Доказательство:
Пусть в графе более $2 cdot sqrt{E}$ тяжелых вершин. Тогда число ребер в графе больше, чем $frac{2 cdot sqrt{E} cdot sqrt{E}}{2} = E$, чего не может быть.
Нахождение количества треугольников в графе за $O(E sqrt E)$
Мысленно разобьем все вершины графа на легкие и тяжелые. Заметим, что треугольников, образованных только тяжелыми вершинами, всего $O(Esqrt{E})$, как $C^3_{sqrt{E}}$. Теперь рассмотрим треугольники, которые содержат в себе легкие вершины. В таком треугольнике точно будут два ребра, инцидентных легкой вершине. Сколько таких пар может быть? Всего таких ребер $O(E)$, при этом для каждого ребра парными могут быть только $O(sqrt{E})$ ребер, в силу степени легкой вершины. Таким образом, textit{число треугольников в графе равно} $O(E sqrt{E})$.
Каким алгоритмом их искать? Можно явно провести процесс, описанный выше, но это не самое приятное в реализации решение этой задачи.
Можно переориентировать ребра от вершин с меньшей степенью к вершинам с большей. Теперь верно следующее
Утверждение:
Из каждой вершины выходит не более $O(sqrt E)$ ребер
Доказательство:
Степень легких вершин $O(sqrt E)$, а из тяжелых вершин ребра идут только в тяжелые, которых всего $O(sqrt E)$.
Теперь для каждой вершины пометим ее соседей, после чего запустим поиск путей длины 2 и будем фиксировать треугольник при нахождении пометки. Для каждого первого ребра пути мы посмотрим на $O(sqrt E)$ ребер, поэтому итоговая сложность алгоритма $O(E sqrt E)$
Автор конспекта: Константин Амеличев
По всем вопросам пишите в telegram @kik0s
Given a Graph, count number of triangles in it. The graph is can be directed or undirected.
Example:
Input: digraph[V][V] = { {0, 0, 1, 0},
{1, 0, 0, 1},
{0, 1, 0, 0},
{0, 0, 1, 0}
};
Output: 2
Give adjacency matrix represents following
directed graph.
We have discussed a method based on graph trace that works for undirected graphs. In this post a new method is discussed with that is simpler and works for both directed and undirected graphs.
The idea is to use three nested loops to consider every triplet (i, j, k) and check for the above condition (there is an edge from i to j, j to k and k to i)
However in an undirected graph, the triplet (i, j, k) can be permuted to give six combination (See previous post for details). Hence we divide the total count by 6 to get the actual number of triangles.
In case of directed graph, the number of permutation would be 3 (as order of nodes becomes relevant). Hence in this case the total number of triangles will be obtained by dividing total count by 3. For example consider the directed graph given below
Following is the implementation.
C++
#include<bits/stdc++.h>
#define V 4
using namespace std;
int countTriangle(int graph[V][V],
bool isDirected)
{
int count_Triangle = 0;
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
for (int k = 0; k < V; k++)
{
if (graph[i][j] && graph[j][k]
&& graph[k][i])
count_Triangle++;
}
}
}
isDirected? count_Triangle /= 3 :
count_Triangle /= 6;
return count_Triangle;
}
int main()
{
int graph[][V] = { {0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
int digraph[][V] = { {0, 0, 1, 0},
{1, 0, 0, 1},
{0, 1, 0, 0},
{0, 0, 1, 0}
};
cout << "The Number of triangles in undirected graph : "
<< countTriangle(graph, false);
cout << "nnThe Number of triangles in directed graph : "
<< countTriangle(digraph, true);
return 0;
}
Java
import java.io.*;
class GFG {
int V = 4;
int countTriangle(int graph[][],
boolean isDirected)
{
int count_Triangle = 0;
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
for (int k=0; k<V; k++)
{
if (graph[i][j] == 1 &&
graph[j][k] == 1 &&
graph[k][i] == 1)
count_Triangle++;
}
}
}
if(isDirected == true)
{
count_Triangle /= 3;
}
else
{
count_Triangle /= 6;
}
return count_Triangle;
}
public static void main(String args[])
{
int graph[][] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
int digraph[][] = { {0, 0, 1, 0},
{1, 0, 0, 1},
{0, 1, 0, 0},
{0, 0, 1, 0}
};
GFG obj = new GFG();
System.out.println("The Number of triangles "+
"in undirected graph : " +
obj.countTriangle(graph, false));
System.out.println("nnThe Number of triangles"+
" in directed graph : "+
obj.countTriangle(digraph, true));
}
}
Python3
def countTriangle(g, isDirected):
nodes = len(g)
count_Triangle = 0
for i in range(nodes):
for j in range(nodes):
for k in range(nodes):
if(i != j and i != k
and j != k and
g[i][j] and g[j][k]
and g[k][i]):
count_Triangle += 1
if isDirected:
return count_Triangle//3
else: return count_Triangle//6
graph = [[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0]]
digraph = [[0, 0, 1, 0],
[1, 0, 0, 1],
[0, 1, 0, 0],
[0, 0, 1, 0]]
print("The Number of triangles in undirected graph : %d" %
countTriangle(graph, False))
print("The Number of triangles in directed graph : %d" %
countTriangle(digraph, True))
C#
using System;
class GFG {
const int V = 4;
static int countTriangle(int[, ] graph, bool isDirected)
{
int count_Triangle = 0;
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
for (int k = 0; k < V; k++)
{
if (graph[i, j] != 0
&& graph[j, k] != 0
&& graph[k, i] != 0)
count_Triangle++;
}
}
}
if (isDirected != false)
count_Triangle = count_Triangle / 3;
else
count_Triangle = count_Triangle / 6;
return count_Triangle;
}
static void Main()
{
int[, ] graph = new int[4, 4] { { 0, 1, 1, 0 },
{ 1, 0, 1, 1 },
{ 1, 1, 0, 1 },
{ 0, 1, 1, 0 } };
int[, ] digraph = new int[4, 4] { { 0, 0, 1, 0 },
{ 1, 0, 0, 1 },
{ 0, 1, 0, 0 },
{ 0, 0, 1, 0 } };
Console.Write("The Number of triangles"
+ " in undirected graph : "
+ countTriangle(graph, false));
Console.Write("nnThe Number of "
+ "triangles in directed graph : "
+ countTriangle(digraph, true));
}
}
PHP
<?php
$V = 4;
function countTriangle($graph,
$isDirected)
{
global $V;
$count_Triangle = 0;
for($i = 0; $i < $V; $i++)
{
for($j = 0; $j < $V; $j++)
{
for($k = 0; $k < $V; $k++)
{
if ($graph[$i][$j] and $graph[$j][$k]
and $graph[$k][$i])
$count_Triangle++;
}
}
}
$isDirected? $count_Triangle /= 3 :
$count_Triangle /= 6;
return $count_Triangle;
}
$graph = array(array(0, 1, 1, 0),
array(1, 0, 1, 1),
array(1, 1, 0, 1),
array(0, 1, 1, 0));
$digraph = array(array(0, 0, 1, 0),
array(1, 0, 0, 1),
array(0, 1, 0, 0),
array(0, 0, 1, 0));
echo "The Number of triangles in undirected graph : "
, countTriangle($graph, false);
echo "nThe Number of triangles in directed graph : "
, countTriangle($digraph, true);
?>
Javascript
<script>
let V = 4;
function countTriangle(graph, isDirected)
{
let count_Triangle = 0;
for(let i = 0; i < V; i++)
{
for(let j = 0; j < V; j++)
{
for(let k = 0; k < V; k++)
{
if (graph[i][j] && graph[j][k] &&
graph[k][i])
count_Triangle++;
}
}
}
isDirected ? count_Triangle /= 3 :
count_Triangle /= 6;
return count_Triangle;
}
let graph = [ [ 0, 1, 1, 0 ],
[ 1, 0, 1, 1 ],
[ 1, 1, 0, 1 ],
[ 0, 1, 1, 0 ] ];
let digraph = [ [ 0, 0, 1, 0 ],
[ 1, 0, 0, 1 ],
[ 0, 1, 0, 0 ],
[ 0, 0, 1, 0 ] ];
document.write("The Number of triangles " +
"in undirected graph : " +
countTriangle(graph, false) +
"</br></br>");
document.write("The Number of triangles " +
"in directed graph : " +
countTriangle(digraph, true));
</script>
Output
The Number of triangles in undirected graph : 2 The Number of triangles in directed graph : 2
Comparison of this approach with previous approach:
Advantages:
- No need to calculate Trace.
- Matrix- multiplication is not required.
- Auxiliary matrices are not required hence optimized in space.
- Works for directed graphs.
Disadvantages:
- The time complexity is O(n3) and can’t be reduced any further.
This article is contributed by Ashutosh Kumar. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
21 Jan, 2022
Like Article
Save Article
Количество треугольников в графе
Алиса и Боб больше не играют ни в какие игры; теперь они дружно изучают свойства различных графов. Алиса придумала следующее занятие: из полного неориентированного графа с n вершинами она выбирает какие-то m ребер и оставляет их себе. Оставшиеся же 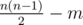
Алисе и Бобу очень нравятся «треугольники» в графах, то есть циклы длины 3. Поэтому они хотят узнать ответ на такой вопрос: какое суммарное количество треугольников находится в двух графах, образованных ребрами Алисы и ребрами Боба, соответственно?
Первая строка содержит два целых числа n и m ( 1 ≤ n ≤ 10 6 , 0 ≤ m ≤ 10 6 ), разделенные пробелом — количество вершин в изначальном полном графе, а также количество ребер в графе Алисы, соответственно. Далее следуют m строк: i -тая строка содержит два целых числа a i , b i ( 1 ≤ a i, b i ≤ n , a i ≠ b i ), разделенные пробелом — номера двух вершин, соединенных i -тым ребром графа Алисы. Гарантируется, что граф Алисы не содержит кратных ребер и петель. Изначальный полный граф также не содержит кратных ребер и петель.
Считайте, что вершины графа пронумерованы некоторым образом от 1 до n .
Выведите единственное число — суммарное количество циклов длины 3 в графах Алисы и Боба.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin , cout или спецификатор %I64d .
Каков эффективный алгоритм подсчета числа треугольников в графе?
каков эффективный алгоритм подсчета количества треугольников в неориентированном графе ) (где граф-это набор вершин и ребер)? Я искал Google и читал на полке учебники по несколько часов каждый день в течение трех дней подряд.
Это для домашнего задания, где мне нужен такой алгоритм, но разработка его ничего не значит на задании. Предполагается, что мы можем просто найти такой алгоритм извне ресурсы, но я на пределе.
для уточнения треугольник на графике представляет собой цикл длиной три. Фокус в том, что он должен работать на множествах вершин не более 10 000 узлов.
в настоящее время я работаю на C#, но больше забочусь об общем подходе к решению этой проблемы, чем о коде для копирования и вставки.
на высоком уровне, мои попытки до сих пор включено:
- широкий первый поиск, который отслеживал все уникальные циклы длины три. Это казалось мне прекрасной идеей, но я не мог заставить ее работать
- цикл по всем узлам в графе, чтобы увидеть, разделяют ли три вершины ребро. Это слишком медленное время работы для больших наборов данных. O (n^3).
сам алгоритм является частью вычисления коэффициента кластеризации.
6 ответов
эта проблема так же сложна, как умножение матрицы. Увидеть это ссылка.
вы знаете что-нибудь о графиках? Они редкие? Если нет, я не думаю, что вы сделаете намного лучше, чем O(n^3).
вам понадобится глубина первый поиск. Алгоритм такой:
1) для текущего узла прошу всех непосещенных смежных вершин
2) для каждого из этих узлов запустите depth two проверьте, является ли узел на глубине 2 вашим текущим узлом с шага one
3) отметить текущий узел как посещенный
4) Сделайте каждый незваный соседний узел своим текущим узлом (1 на 1) и запустите тот же алгоритм
зависит от того, как представлены ваши графики.
Если у вас есть матрица смежности A, Число треугольников должно быть tr (a^3)/6, другими словами, в 1/6 раза больше суммы диагональных элементов (разделение заботится об ориентации и вращении).
Если у вас есть списки смежности, просто начните с каждого узла и выполните поиск глубины-3. Подсчитайте, как часто вы достигаете этого узла — > разделить на 6 снова.
подсчет треугольников действительно труден и вычислительно дорогостоящ. Возможно, это хорошая отправная точка для понимания, почему:эффективный подсчет треугольников в больших графах с помощью разбиения вершин на градусы.
соответствующий цикл должен проверить для каждого из n узлов против каждого из их соседей(n*(n-1)) и продолжить цикл, чтобы увидеть, являются ли соседи соседа соседа n: (n*(n-1)) (n-1) (n-1), что почти 10^16 для 10000 n. С миллионом узлы эти петли становятся глупыми, но для ваших 10000 у вас не должно быть никаких проблем, если вы хотите, чтобы brute-force it:)
вы упомянули, что кодируете на C#, а graph (который доступен для C) имеет отличный алгоритм подсчета треугольников, написанных Габором Csardi. Он насчитал 1,3 миллиона треугольников в моем случайном графике 10000 узлов и один миллион ребер за 1,3 секунды на пятилетнем ноутбуке:) Габор Csardi был бы парнем, чтобы спросить 
С точки зрения разных программные подходы, возможно, вам стоит посмотреть на данные, в которых вы храните свою сеть. Если хранится в матрице смежности, количество циклов фиксировано,но в списке ребер сети из трех ребер количество циклов кратно трем независимым от количества узлов. Вы можете запросить список ребер для соседей узла, не проверяя каждую комбинацию i — >j.
Я написал педагогический сценарий в R, чтобы проиллюстрировать подходы и измерить различные скорость алгоритмов очень простой способ. Есть много проблем со скоростью, присущих использованию R здесь (версия edge-list полностью завалена слишком большим количеством ребер), но я думаю, что пример кода должен получить некоторые идеи о том, как думать о скорости грубого принуждения треугольника. Это в R, и не очень аккуратно, но хорошо прокомментирован. Надеюсь, вы сможете преодолеть языковой барьер.
Если вас не волнует точное количество треугольников, существует очень простой алгоритм потоковой передачи, который обеспечивает беспристрастную оценку. См., например,здесь для объяснений.
самый быстрый алгоритм, известный для поиска и подсчета треугольников, опирается на быстрое матричное произведение и имеет временную сложность O(nw), где ω
Количество треугольников в неориентированном графе
Учитывая неориентированный простой граф, нам нужно найти, сколько треугольников у него может быть. Например, приведенный ниже график содержит 2 треугольника.
Пусть A [] [] будет матричным представлением графа смежности. Если мы вычислим A 3 , то число треугольников в Undirected Graph будет равно trace (A 3 ) / 6. Где trace (A) — это сумма элементов на главной диагонали матрицы A.
Ниже приведена реализация вышеприведенной формулы.
// C ++ программа для поиска
// количество треугольников в
// Неориентированный граф. Программа
// для матрицы смежности
// представление графика
#include
using namespace std;
// Количество вершин в графе
#define V 4
// Функция полезности для матрицы
// умножение
void multiply( int A[][V], int B[][V], int C[][V])
for ( int i = 0; i
for ( int j = 0; j
for ( int k = 0; k
// Сервисная функция для расчета
// трассировка матрицы (сумма
// диагностические элементы)
int getTrace( int graph[][V])
for ( int i = 0; i
// Сервисная функция для расчета
// количество треугольников в графе
int triangleInGraph( int graph[][V])
// Сохранить график ^ 2
// Сохранить график ^ 3
for ( int i = 0; i
for ( int j = 0; j
aux2[i][j] = aux3[i][j] = 0;
// aux2 — это график ^ 2 теперь printMatrix (aux2);
multiply(graph, graph, aux2);
// после этого умножения aux3
// график ^ 3 printMatrix (aux3);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
printf ( «Total number of Triangle in Graph : %dn» ,
// Java программа для поиска номера
// треугольников в неориентированном
// График. Программа для
// матричное представление смежности
// графика
// Количество вершин в
// Сервисная функция для
void multiply( int A[][], int B[][],
for ( int i = 0 ; i
for ( int j = 0 ; j
for ( int k = 0 ; k
// Сервисная функция для расчета
// трассировка матрицы (сумма
int getTrace( int graph[][])
for ( int i = 0 ; i
// Сервисная функция для
// треугольники на графике
int triangleInGraph( int graph[][])
// Сохранить график ^ 2
int [][] aux2 = new int [V][V];
// Сохранить график ^ 3
int [][] aux3 = new int [V][V];
// Инициализация вспомогательных матриц
for ( int i = 0 ; i
for ( int j = 0 ; j
aux2[i][j] = aux3[i][j] = 0 ;
// aux2 теперь граф ^ 2
multiply(graph, graph, aux2);
// после этого умножения aux3
// является графиком ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6 ;
public static void main(String args[])
Directed obj = new Directed();
System.out.println( «Total number of Triangle in Graph : » +
// Этот код предоставлен Аншикой Гоял.
# Программа Python3 для определения количества
# треугольники в неориентированном графе.
# программа для матрицы смежности
# представление графа
# Функция полезности для матрицы
# умножение
def multiply(A, B, C):
for i in range (V):
for j in range (V):
for k in range (V):
# Сервисная функция для расчета
# след матрицы (сумма
# диагностические элементы)
for i in range (V):
# Полезная функция для расчета
количество треугольников на графике
# Хранить график ^ 2
aux2 = [[ None ] * V for i in range (V)]
# Хранить график ^ 3
aux3 = [[ None ] * V for i in range (V)]
for i in range (V):
for j in range (V):
aux2[i][j] = aux3[i][j] = 0
# aux2 — это график ^ 2 теперь printMatrix (aux2)
multiply(graph, graph, aux2)
# после этого умножения aux3
# graph ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3)
return trace / / 6
# Количество вершин в графе
graph = [[ 0 , 1 , 1 , 0 ],
print ( «Total number of Triangle in Graph :» ,
# Этот код предоставлен PranchalK
// C # программа для поиска номера
// треугольников в неориентированном
// График. Программа для
// матричное представление смежности
// графика
<
// Количество вершин
// в графе
// Сервисная функция для
// матричное умножение
void multiply( int [,]A, int [,]B,
for ( int i = 0; i
for ( int j = 0; j
for ( int k = 0; k
// Функция полезности для
// вычислить след
// матрица (сумма
// диагностические элементы)
int getTrace( int [,]graph)
for ( int i = 0; i
trace += graph[i, i];
// Сервисная функция для
// вычисляем количество
// треугольники на графике
int triangleInGraph( int [,]graph)
// Сохранить график ^ 2
int [,] aux2 = new int [V, V];
// Сохранить график ^ 3
int [,] aux3 = new int [V, V];
// Инициализация вспомогательных матриц
for ( int i = 0; i
for ( int j = 0; j
aux2[i, j] = aux3[i, j] = 0;
// aux2 теперь граф ^ 2
multiply(graph, graph, aux2);
// после этого умножения aux3
// является графиком ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
public static void Main()
GFG obj = new GFG();
Console.WriteLine( «Total number of » +
«Triangle in Graph : » +
// Этот код предоставлен anuj_67.
Выход:
Как это работает?
Если мы вычисляем A n для представления графа в матрице смежности, то значение A n [i] [j] представляет количество различных переходов между вершинами i по j в графе. В A 3 мы получаем все различные пути длины 3 между каждой парой вершин.
Треугольник — это циклический путь длины три, т.е. начинается и заканчивается в одной и той же вершине. Таким образом, A 3 [i] [i] представляет треугольник, начинающийся и заканчивающийся вершиной i. Поскольку у треугольника есть три вершины, и он считается для каждой вершины, нам нужно разделить результат на 3. Кроме того, поскольку граф является ненаправленным, каждый треугольник в два раза больше, чем ipqj и iqpj, поэтому мы также делим на 2. Следовательно, количество треугольников является следом (A 3 ) / 6.
Сложность времени:
Временная сложность вышеупомянутого алгоритма составляет O (V 3 ), где V — количество вершин в графе, мы можем улучшить производительность до O (V 2.8074 ), используя алгоритм умножения матриц Штрассена .
Эта статья предоставлена Уткаршем Триведи. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
http://askdev.ru/q/kakov-effektivnyy-algoritm-podscheta-chisla-treugolnikov-v-grafe-122592/
http://espressocode.top/number-of-triangles-in-a-undirected-graph/
Alice and Bob don’t play games anymore. Now they study properties of all sorts of graphs together. Alice invented the following task: she takes a complete undirected graph with n vertices, chooses some m edges and keeps them. Bob gets the 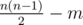
Alice and Bob are fond of «triangles» in graphs, that is, cycles of length 3. That’s why they wonder: what total number of triangles is there in the two graphs formed by Alice and Bob’s edges, correspondingly?
Input
The first line contains two space-separated integers n and m (1 ≤ n ≤ 106, 0 ≤ m ≤ 106) — the number of vertices in the initial complete graph and the number of edges in Alice’s graph, correspondingly. Then m lines follow: the i-th line contains two space-separated integers ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi), — the numbers of the two vertices connected by the i-th edge in Alice’s graph. It is guaranteed that Alice’s graph contains no multiple edges and self-loops. It is guaranteed that the initial complete graph also contains no multiple edges and self-loops.
Consider the graph vertices to be indexed in some way from 1 to n.
Output
Print a single number — the total number of cycles of length 3 in Alice and Bob’s graphs together.
Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is advised to use the cin, cout streams or the %I64d specifier.
Note
In the first sample Alice has 2 triangles: (1, 2, 3) and (2, 3, 4). Bob’s graph has only 1 triangle : (1, 4, 5). That’s why the two graphs in total contain 3 triangles.
In the second sample Alice’s graph has only one triangle: (1, 2, 3). Bob’s graph has three triangles: (1, 4, 5), (2, 4, 5) and (3, 4, 5). In this case the answer to the problem is 4.
Машинное обучение на графах, часть 1
Сбор базовой статистики
В серии публикаций я сделаю обзор нескольких подходов машинного обучения к обучению на основе данных графов. Начав с базовой статистики, которая используется для описания графов, я углублюсь в предмет, обсудив вложения узлов, ядра графов, обработку сигналов графов и, в конечном итоге, нейронные сети графов. Эти сообщения предназначены для отражения моего личного опыта в академических кругах и промышленности, включая некоторые из моих исследовательских работ. Моя основная мотивация — сначала представить некоторые базовые подходы к машинному обучению на графах, которые следует использовать, прежде чем углубляться в продвинутые алгоритмы, такие как нейронные сети на графах.
В первом посте я представляю некоторые общие методы анализа графиков, которые должны помочь нам лучше понять наши данные.
Предварительные мероприятия
Я предполагаю знакомство с основными концепциями графов. Я буду рассматривать неориентированные графы без петель (узлы, соединенные между собой ребром), но это только для простоты представления. Граф обозначается G = (V, E), где V — это набор узлов или вершин, а E — это набор ребер. . Количество узлов обозначается n = | V | и количество ребер на m = | E |.
Какую статистику на графике искать?
Прежде чем приступить к работе над проблемой, мы обычно тратим некоторое время на исследовательский анализ данных. Это дает нам представление о данных, которые могут иметь решающее значение для нашей дальнейшей работы. В идеале мы хотели бы построить график, как мы это делаем для карты метро, но большинство реальных графиков большие и их так легко представить визуально. Вместо этого вот некоторые важные статистические данные, на которые стоит обратить внимание:
- Распределение степеней. Степенное распределение двух реальных сетей показано на рисунке 1. Первый график получен из электронной переписки в учреждении ЕС, а второй график — это граф соавторства из базы данных DBLP. Мы заметили, что наиболее распространенная степень узла в графе электронной почты — 1, что означает, что большинство людей общаются только с одним человеком. В графе соавторства у большинства авторов есть два-три соавтора.
- Плотность графика. Количество определяется как
Объяснение простое: максимально возможное количество ребер равно n * (n-1) / 2, поскольку каждый узел может быть связан ровно с n-1 другими узлами, а ребра неориентированы. Он измеряет, насколько близок граф к полносвязному графу или клике. Большинство реальных сетей очень разрежены, поэтому этот показатель в большинстве случаев не очень информативен.
- Подключенные компоненты. Мы говорим, что узел u достижим из узла v, если существует путь, последовательность ребер, между u и v. В связном компоненте каждый узел доступен из любого другого узла в компоненте. Количество и соответствующий размер связанных компонентов могут предоставить информацию о графе. Однако в большинстве случаев нас интересуют связные графы, состоящие из одной компоненты связности.
- Диаметр графика. Кратчайший путь между двумя узлами u и v — это минимальное количество ребер, которые необходимо пройти, чтобы достичь v после запуска в u. Диаметр графа — это максимальная длина кратчайшего пути между любыми двумя узлами графа. Если граф имеет более одной компоненты связности, то его диаметр бесконечен. В таком случае нас интересует диаметр каждого связного компонента. Диаметр графа можно использовать, чтобы различать разные типы сетей. Например, сети метро, вероятно, будут иметь больший диаметр, чем небольшие социальные сети.
- Количество треугольников и коэффициент транзитивности. В теории графов есть фундаментальное понятие графы Эрдеша – Реньи. Это теоретическая модель, в которой ребра между узлами генерируются случайным образом, каждое с фиксированной вероятностью p, независимо от других ребер. Реальные графы сильно отличаются от графов Эрдеша – Реньи, поскольку рёбра не создаются случайным образом независимо друг от друга. В частности, для большинства реальных графиков часто считается, что друзья моих друзей также являются моими друзьями. Это побудило исследователей рассматривать треугольники как фундаментальную единицу в аналитике графов [1]. На высоком уровне количество треугольников показывает, насколько наш график отличается от случайного.
Коэффициент транзитивности графа определяется как
В приведенном выше числителе указано количество треугольников, умноженное на 3, а знаменатель обозначает количество 2-путей в графе, которые можно вычислить как:
На графике на рисунке 2 есть два треугольника, а именно (u, v, w) и (u, v, z). 2-пути — это последовательности из 3 узлов, соединенных ребром, например z-u-w. Обратите внимание, что каждая пара соседей данного узла приводит к 2-пути, отсюда приведенная выше формула для общего количества 2-путей. Мы умножаем количество треугольников на 3, потому что мы считаем каждый из трех его 2-путей. Таким образом, коэффициент транзитивности — это значение от 0 (отсутствие треугольников) до 1 (полносвязные графики).
На рисунке 2 количество 2-трактов равно 8, поэтому коэффициент транзитивности равен 0,75.
В большинстве реальных графиков коэффициент транзитивности постоянен. Чем больше коэффициент транзитивности, тем сильнее связана сеть. Фактически, он был введен в 1998 году для описания модели сетей малого мира.
- Локальное количество треугольников и коэффициент кластеризации. Определен коэффициент локальной кластеризации узла u.
то есть количество треугольников, в которых вершиной u является узел, деленное на количество 2-путей с центром в u.
Затем это обобщается на глобальный коэффициент кластеризации
На рисунке 2 узел u имеет коэффициент локальной кластеризации 2/3, а коэффициент глобальной кластеризации графа равен (2/3 + 2/3 + 1 + 1) / 4 = 0,833.
Наконец, мы хотели бы отметить, что в литературе коэффициент транзитивности иногда называют коэффициентом кластеризации, а глобальный коэффициент кластеризации, как определено выше, называется средним коэффициентом кластеризации. Путаница в обозначениях проистекает из того факта, что Уоттс и Строгац ошибочно заявили в своей основополагающей статье [1], что коэффициент транзитивности и коэффициент кластеризации идентичны.
Как посчитать количество треугольников?
Из приведенного выше обсуждения очевидно, что наиболее важной статистикой графа является количество треугольников и соответствующие коэффициенты транзитивности и кластеризации. Посмотрим, как это вычислить. Я рекомендую использовать Python библиотеку networkx при работе с графиками. Он прост и интуитивно понятен в использовании и предоставляет множество фундаментальных алгоритмов графов, таких как кратчайшие пути, количество связанных компонентов и даже коэффициент транзитивности.
import networkx as nx
import numpy as np
G = nx.Graph()
for u, v in <list of edges or edge generator>:
G.add_edge(u, v)
Мы можем подсчитывать треугольники, используя третью степень матрицы смежности графа. Точная формула:
След определяется как сумма диагональных элементов матрицы. Каждая диагональная запись в A³ измеряет количество путей длиной ровно 3 от соответствующего узла до самого себя. Рассмотрим треугольник между тремя узлами (u, v, w). Есть 6 перестановок этих трех узлов, поэтому нам нужно разделить трассу на 6. В Python код выглядит как
def count_triangles(G): A = nx.to_scipy_sparse_matrix(G) A2 = A.dot(A) A3 = A2.dot(A) return A3.diagonal().sum()/6
Обратите внимание, что выше используется умножение разреженных матриц. Однако не гарантируется, что третья степень матрицы смежности будет разреженной, особенно для графов небольшого диаметра, и вычисления могут стать узким местом. В таком случае я рекомендую использовать алгоритм Дулиона [2]. Doulion работает, выбирая ребра из исходного графа. Каждое ребро сохраняется с вероятностью p. Таким образом, треугольник выживает в разреженном графе с вероятностью p³. Мы оцениваем количество треугольников в исходном графе, умножая количество треугольников в разреженном графе на 1 / p³.
def sparsify_graph(G, p):
G_sparse = nx.Graph()
for u,v in G.edges():
if np.random.random() <= p:
G_sparse.add_edge(u,v)
return G_sparse
Провожу эксперимент с графом, полученным из сети DBLP. Граф состоит из 317 080 узлов и чуть более 1 миллиона ребер. Путем выборки рёбер с вероятностью 10% я получил следующее время работы для алгоритма точного подсчета и для Doulion. И достигнутое приближение количества треугольников отличное.
Elapsed time exact: 13.21 secs Elapsed time Doulion: 1.19 secs Approximation exact/estimated: 1.030
Еще немного расширенной статистики.
Вкратце отметим, что есть и более продвинутая статистика графов.
- Центральность посредничества. Эта мера фиксирует влияние узлов на графике. Для каждого узла u мы подсчитываем, сколько кратчайших путей между парами узлов проходит через u. Узлы с высокой промежуточностью считаются более важными в сети. Распределение оценок центральности промежуточности позволяет нам лучше понять структуру графа. Однако вычислительная сложность для вычисления центральности для всех узлов составляет O (m * n).
- Плотно связанные подграфы. Важной темой исследования является обнаружение плотносвязных подграфов [3]. Это подграфы в исходном графе, где почти все пары узлов соединены ребром. Это основа алгоритмов обнаружения сообществ. Но количество и плотность этих плотных компонентов также являются важной статистикой.
- Мотивы графов майнинга. Выявление частых графических паттернов — активная область исследований [4]. Он обобщает алгоритмы подсчета треугольников на поиск и подсчет более сложных подграфов или мотивов . Эти подсчеты можно использовать в задачах классификации графов. На рисунке 3 я показываю три разных мотива на 4 узлах. Однако подсчет мотивов может быть дорогостоящим в вычислительном отношении и ограничен небольшими подграфами. Можно утверждать, что успех нейронных сетей с графами основан на их способности изучать сложные мотивы, относящиеся к рассматриваемой проблеме.
Код
Код для приведенных выше примеров можно найти по адресу: https://github.com/konstantinkutzkov/ML_on_graphs/
[1] Дункан Дж. Уоттс, Стивен Х. Строгац. Коллективная динамика сетей« маленького мира ». Nature 393, 1998.
[2] Харалампос Э. Цуракакис, У Канг, Гэри Л. Миллер и Христос Фалаутсос. ДОУЛЬ: Счет треугольников в массивных графах с монетой. КДД 2009.
[3] Харалампос Э. Цуракакис, Франческо Бонки, Аристидес Гионис,
Франческо Гулло и Мария А. Циарли. Плотнее, чем самый плотный подграф:
Извлечение оптимальных квазиклик с гарантиями качества. КДД 2013.
[4] Гую Хан и Хариш Сетху. Болтливое блуждание: быстрый и точный анализ статистики мотивов в больших графах. ICDM 2016.












