Значащие цифры десятичного числа – это все его цифры, начиная с первой ненулевой слева.
Пример 1
x = 0.002036, цифры 2036 являются значащими;
x = 2.27×106, значащими цифрами являются цифры 2, 2, 7;
x = 2270000, все цифры этого числа являются значащими.
Значащая цифра в записи числа верна, если абсолютная погрешность числа меньше или равна пяти единицам разряда, следующего за этой цифрой.
Пример 2
Определить, сколько верных значащих цифр содержит число:
x = 0.002306 ± 0.00001.
Для определения числа верных значащих цифр запишем x и Dx таким образом, чтобы легко было сравнить разряды этих чисел:
x = 0.002306, абсолютная погрешность Dx = 0.00001.
x = 0.002306,
Dx = 0.00001.
Третья значащая цифра (0) не может быть верной, так как она одного порядка с погрешностью. Верными могут быть цифры, которые стоят перед ней (2, 3). Цифра 3 будет верной, если Dx £ 0.00005. В нашем случае это условие выполнено, следовательно, 2, 3 – верные значащие цифры.
Цифры в записи числа, следующие за верными, называются сомнительными.
Пример 3
x = 1.121 ± 0.003;
x = 1.121;
Dx = 0.003.
В числе x = 1.121 три верные значащие цифры (1, 1, 2) и одна сомнительная (1).
Пример 4
x = 0.002306 ± 0.00007;
x = 0.002306;
Dx = 0.00007.
В числе x = 0.002306 одна верная значащая цифра (2), три сомнительные (3, 0, 6).
Пример 5
x = 12.3 ± 0.5;
x = 12.3;
Dx = 0.5.
В числе x = 12.3 три значащие цифры, две верные значащие цифры (1, 2), одна сомнительная (3).
Пример 6
x = 12.3 ± 0.8;
x = 12.3;
Dx = 0.8.
В числе x = 12.3 одна верная значащая цифра (1), две сомнительные (2, 3).
При записи абсолютной и относительной погрешностей используют, как правило, одну-две значащие цифры. Приближенные числа принято записывать следующим образом: сначала записывают все верные значащие цифры, затем одну-две сомнительные. То есть в записи приближенного числа, как правило, число значащих цифр на одну-две больше, чем число верных значащих цифр.
Практическое правило. Одна верная значащая цифра в записи числа соответствует приблизительно относительной погрешности 10 %. И наоборот, относительная погрешность 10 % соответствует приблизительно одной верной значащей цифре. Две верные значащие цифры соответствуют относительной погрешности 1 %, три верные значащие цифры – относительной погрешности 0.1 %.
Верные значащие цифры приближенного числа
Определение
5:
Значащими
цифрами
числа а
называют все цифры в его записи, начиная
с первой ненулевой слева.
Пример 5:
Числа 0,001405и 5,0300 имеют соответственно
4 и 5 значащих цифр. Ноль, записанный в
конце десятичной дроби, всегда значащая
цифра. В числе 5,0300 последний ноль
показывает, что число задано с точностью
до десятитысячных.
Определение
6:
Значащую цифру числа
а
называют верной,
если абсолютная погрешность числа не
превосходит половины единицы разряда,
соответствующего этой цифре.
Пример 6:
Сколько верных значащих цифр содержит
приближенное число
?
Решение:
Поскольку
,
то верными будут цифры 5, 8, 2.
Погрешности математических операций Абсолютная погрешность суммы и разности
Теорема 1:
Абсолютная
погрешность
алгебраической
суммы
нескольких приближенных чисел не
превышает суммы алгебраических
погрешностей этих чисел.
Доказательство:
Пусть
— алгебраическая сумма точных чисел.
— сумма приближенных значений этих
чисел.
Абсолютные
погрешности их соответственно равны:
.
Вычитая из точного значения суммы её
приближенное значение, имеем:
или, переходя к
модулям:
,
следовательно
,
что требовалось
доказать.
Из последней
формулы следует, что абсолютная
погрешность алгебраической суммы не
может быть меньше абсолютной погрешности
наименее точного из слагаемых.
Пример 7:
,
где числа 204,4 и
144,2 верны с точностью до 0,1.
Значит, остальные
нужно округлить с точностью до 0,01,
сложить и округлить результат до 0,1.
Итак
Относительная погрешность произведения нескольких приближенных чисел
Теорема 2:
Относительная
погрешность произведения
нескольких
приближенных чисел, отличных от нуля,
не превышает суммы относительных
погрешностей этих чисел.
Доказательство:
Пусть
(1), где
— положительные
приближенные числа и их абсолютные
погрешности:
.
Логарифмируя (1),
получим:
.
По теореме об
абсолютной погрешности суммы:
.
Используя то, что
,
получим
,
что требовалось
доказать.
Относительная погрешность частного
Теорема 3:
Относительная
погрешность частного не превышает суммы
относительных погрешностей делимого
и делителя.
Доказательство:
Пусть
— приближенные числа, а
— абсолютные погрешности этих чисел.
По теореме об абсолютной погрешности
алгебраической суммы:
,
что требовалось
доказать.
Относительная погрешность натуральной степени и корня
Теорема 4:
Относительная погрешность m-й
степени
приближенного числа (m-натуральное)
в m
раз больше относительной
погрешности
самого числа.
Доказательство:
Пусть
,
тогда
,
что требовалось
доказать.
Вывод:
В результате вычисления степени
приближенного числа следует оставить
столько верных значащих цифр, сколько
верных значащих цифр в основании.
Теорема 5:
Относительная
погрешность
корня m-й
степени в m
раз меньше предельной относительной
погрешности
подкоренного числа.
Доказательство:
Пусть
,
тогда
,
т.е.
.
Правила подсчета цифр
При массовых
вычислениях с приближенными или точными
числами, а также с числами, у которых
погрешность отсутствует, используют
правила
подсчета цифр:
-
промежуточные
вычисления следует получать хотя бы
с одной запасной цифрой, по отношению
к значащим цифрам
чисел,
участвующим в промежуточном вычислении, -
окончательный
результат вычисления содержит то
количество значащих цифр, которое
имеет исходное число с наименьшим
числом значащих цифр.
Пример 8:
Вычислить выражение: Y
= 0,125а2
(8b-c),
где a
= 18; b
= 2,75; c
= 3,232.
Решение:.
Так как погрешность чисел а,b,с
отсутствует
то вычисления производим в соответствии
с правилами подсчета цифр.
Преобразуем
исходное выражение к следующему, более
рациональному виду :
Y =.0,125а2
(8b-c)
= a2
(b-c/8)
Исходное выражение
содержало 5 действий, а окончательное
выражение содержит 4 действия.
Далее последовательно
производим необходимые вычисления (в
соответствии с числом а
= 18, у которого
две значащие цифры) и записываем результат
в форме с плавающей запятой:
Y
= 324 • (2,75 —
0,404) = 324 • 2,346 = 760 = 7,6 • 102.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщение от babahs1
Вот числа:
-14 верных цифр
0.043887 — 2 верных цифры
Не понимаю, в чем ошибка (преподаватель не принял)?
И правильно что не принял…
В вашем первом примере число верных цифр равно 5. Почему? А вот запишем это число в виде
6.5392*10-14 = 0,000 000 000 000 065 392
Нули не считаются верными цифрами, сколько бы их впереди не стояло.
Другой пример
6.5392*1014 = 653 920 000 000 000
здесь тоже 5 верных цифр.
Следует отметить, что если бы последнее число было бы точным, то это необходимо специально указывать. Однако запись числа в экспоненциальной форме как правило означает, что число приближённое. И нули не считаются точными цифрами
Только для ТОЧНОГО числа число верных цифр равно числу самих цифр.
Пример:
1 000 000 — 7 верных цифр, если миллион точное число.
В вашем последнем примере (0,043887) — число верных цифр 5, а не 2. В противном случает данное число было бы округлёно до 0,044.
Создатель теории приближенных вычислений А. Н. Крылов говорил: «При производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся». Ему же принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».
Приближенные числа записываются, как правило, при помощи десятичных дробей. Между записью приближенных и точных чисел есть различия. Если перед нами точное число, то вес его цифры являются верными, точными. Что же касается приближенного числа, то некоторые его цифры верны, а другие являются сомнительными.
Цифра десятичного разряда приближенного числа 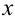
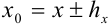
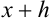
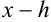
Проверку на верные и сомнительные цифры нужно начинать слева направо с наивысшего разряда. Все цифры, стоящие правее первой найденной сомнительной цифры, автоматически считаются сомнительными.
Пример №45.4.
Найдите верные и сомнительные цифры в записи числа 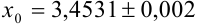
Решение:
Поскольку 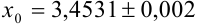

Начинаем проверку на верные и сомнительные цифры с наивысшего разряда — единиц. Видим, что цифры 3,45 одинаковы в левой и правой части двойного неравенства (т.е. в записи 
Цифры в разряде тысячных в правой и левой части двойного неравенства отличаются (1 и 5), следовательно, в записи приближенного числа 3,4531 цифра 3, стоящая в разряде тысячных, и цифра 1, стоящая за ней, являются сомнительными.
Итак, точное число 
Ответ:
Для записи приближенных чисел существуют следующие правила:
- Оставлять в записи числа только верные цифры.
- Если в десятичной дроби последние верные цифры нули, то их надо выписывать.
- Если число содержит на конце целой части сомнительные цифры, то они должны быть заменены на
, где
— число цифр, которые нужно заменить.
- Граница абсолютной погрешности числа, содержащего только верные цифры, равна единице последнего разряда.
Проиллюстрируем применение данных правил на конкретных примерах.
1. Поскольку в записи числа следует оставлять только верные цифры, то в примере 45.4 точное значение 
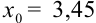
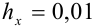
2. Если задано число 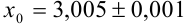

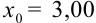
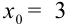
3. Пусть задано число 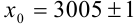

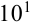
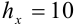
В науке принято записывать числа в стандартном виде, т.е. в виде 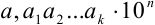
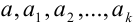
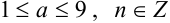
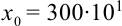
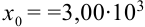
Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой отличной от нуля цифры.
Например, число 0,712 содержит три значащие цифры: 7, 1, 2. Число 0,00012 — две значащие цифры: 1 и 2. Число 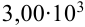
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Известно, что любое положительное число A может быть представлено в виде конечной или бесконечной десятичной дроби
A = Am 10m + am-1 10m-1 + … + am-n+1 10m-n+1 + …,
Где ai – цифры числа A, причем старшая цифра am≠0, а m – некоторое целое число (старший десятичный разряд). Например:
3141,59…= 3∙103 +1∙102 +4 101 +1∙100+ 5∙10-1+9∙10-2+…
На практике преимущественно приходится иметь дело с приближенными числами, представляющими собой конечные десятичные дроби. Значащими цифрами числа Называются все цифры в его записи, начиная с первой ненулевой слева. Например, в числе 0,002080 первые три нуля не являются значащими цифрами, остальные четыре цифры, включая два нуля, будут значащими. В числе 0,00208 значащими цифрами будут три последних цифры.
Значащую цифру приближенного числа называют верной, если абсолютная погрешность этого числа не превосходит единицы разряда, соответствующего этой цифре. Например, для точного числа A=412,3567 число A*=412,356 является приближением с шестью верными знаками, так как D(a*)=0,0007< 1∙10-3.
Таким образом, точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр. Не всегда верные цифры в приближенном числе будут совпадать с соответствующими цифрами точного числа. Например, приближенное число A*= 9,995, заменяющее точное A=10, имеет три верных знака, причем все цифры этих чисел различны.
| < Предыдущая | Следующая > |
|---|



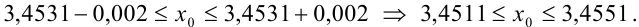
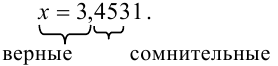
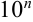 , где
, где  — число цифр, которые нужно заменить.
— число цифр, которые нужно заменить.