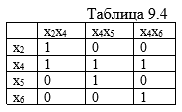
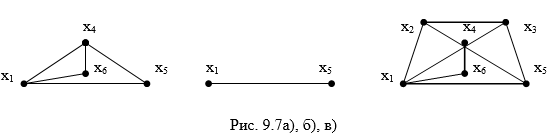
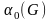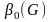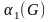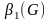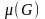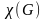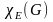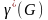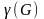Теория графов представляет собой раздел математики, имеющий широкое
практическое применение во многих
областях человеческой деятельности. Математика, физика, химия, теория связи,
электротехника, архитектура, исследование операций, генетика, психология – вот
далеко не полный список областей ее применения
Теория графов становится одной из существенных частей
математического аппарата кибернетики, языком дискретной математики.
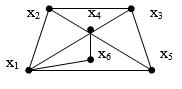
Граф G задается с помощью пары множеств G = (V, R), где V есть множество вершин,
а R –
множество линий, соединяющих пары вершин. Линии со стрелками называются дугами, без стрелок – ребрами. Обычно граф представляют с помощью
схемы, на которой некоторые вершины соединены ребрами (дугами).
Вершинами могут служить объекты любой природы: будь то
населенные пункты, компьютерные сети, элементы блок- схем алгоритмов. Под
ребром могут подразумеваться дороги между соседними городами, линии связи между
компьютерами.
Вершины называются смежными, если их соединяет ребро.
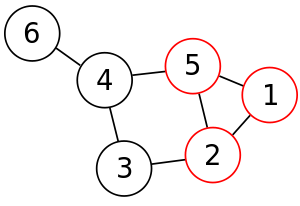
Например, на рис. смежны вершины V1 и V2
, так как их соединяет ребро R12
.
Множество V,
R являются конечными –
мы можем перечислить все вершины и ребра
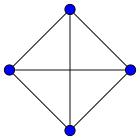
графа. Количество вершин и количество ребер графа определяют мощности множеств V и R. Так, количество вершин графа G ровно 5, а количество ребер
равно 8.
Ребро и любая из его двух вершин называются инцидентными.
Под степенью вершин подразумевается количество инцидентных ей ребер. Так,
степень вершин V1 равно 3, а степень вершин V5
равна 4.
Последовательность чередующихся ребер и вершин графа называется маршрутом.
В графах можно выделить различные
маршруты. Маршрут называется замкнутым, если вершины начала и конца маршрута
совпадают. Если ребра и вершины, образующие маршрут различны, то такой маршрут
называется цепью. Путь в ориентированном графе — это
последовательность дуг, в которой конечная вершина всякой дуги, отличной от
последней, является начальной вершиной следующей.
Длина маршрута равна количеству ребер, входящих в него.
Граф называется связным, если любые две его вершины
можно соединить маршрутом (или путем).
Ориентированные
графы.
Граф, в котором направление линий принципиально называется ориентированным
(орграф). В орграфе каждое ребро имеет одно направление. Такие ребра называются
дугами. Для орграфа вводятся такие понятия, как входящая и исходящая
степени вершины. Это соответственно число входящих в вершину дуг и число исходящих из
нее дуг.
Взвешенные графы.
Взвешенный граф – это граф, в котором с
вершинами и линиями связана некоторая дополнительная информация. Эта информация
называется весом вершины или линии. Вес позволяет отобразить на графе не
только структуру системы, но и различные свойства компонент или связей,
количественная характеристика. Вес сети равен сумме весов ее ребер.
Полный граф
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром. В полном графе каждая его вершина принадлежит одному и тому же числу ребер. Для задания полного графа достаточно знать число его вершин. Полный граф с n
вершинами обычно обозначается через Kn.
Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа G и ребра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа и обозначают его G .
Двудольный граф
Допустим, что множество вершин графа можно разбить на два
непересекающихся подмножества V1 и V2
, так,
что каждое ребро в G соединяет
какую-нибудь вершину из V1 с какой-либо
вершиной из V2 , тогда G называем двудольным
графом. Такие графы иногда обозначают G(V1, V2
) , если хотят выделить два указанных
подмножества. Двудольный граф можно определить и по-другому: в терминах
раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф
называется двудольным, если каждую его вершину можно окрасить красным или синим
цветом так, чтобы любое ребро имело один конец красный, а другой — синий.
Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая
вершина из V1 соединена с каждой вершиной
из V2
; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается Km,n
, где m, n
— число вершин соответственно
в V1 и V2 .
Заметим, что граф Km,n имеет ровно m + n вершин и m*n ребер.
Плоский граф
Плоским графом называется граф, изображенный на плоскости
так, что никакие два его ребра (или, вернее, представляющие их кривые)
геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф,
изоморфный плоскому графу, называется
планарным. Планарный граф можно определить еще так: граф
планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие
два его ребра не пересекаются, если не считать точками пересечения общие
вершины, называют плоским представлением графа. Ясно, что плоское
представление имеет только плоский граф. Обратно, у всякого плоского графа
непременно найдется плоское представление. Плоские графы — это простые циклы,
деревья, лес, а также граф, содержащий цикл, из вершин которого
«выходят» деревья.
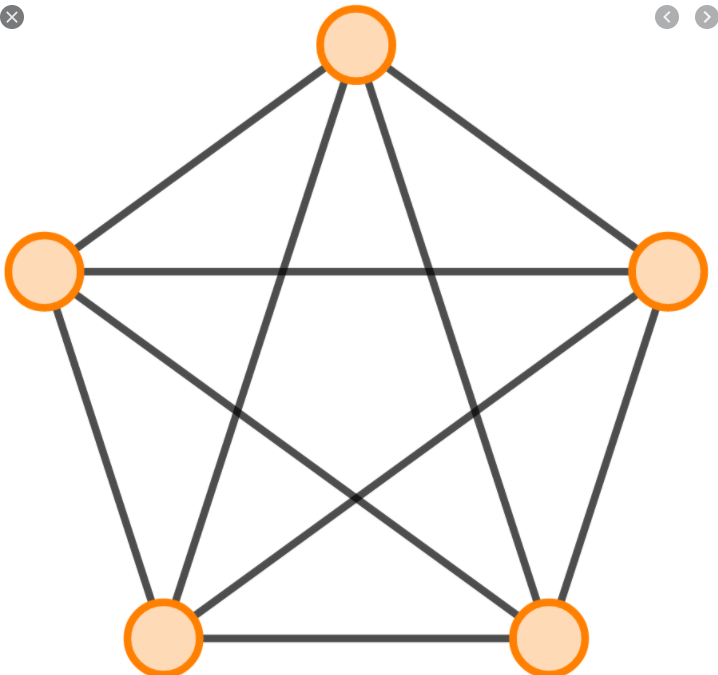
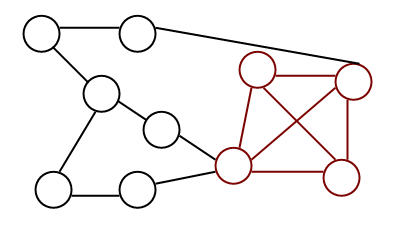
Примером неплоского графа
может служить полный граф с пятью вершинами. Любые попытки начертить его
плоское представление обернутся неудачей.
В качестве характеристики плоского
представления графа вводится понятие грани. Гранью в плоском представлении
графа G называется
часть плоскости, ограниченная простым циклом и не содержащая внутри других
циклов.
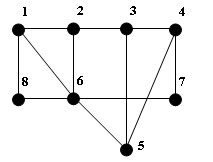
На рисунке показано плоское
представление графа G с тремя гранями: (1, 5,4,1), (1, 3, 2,4,1), (1,2,3,1). Часть плоскости, ограниченная простым циклом (1,2,4,1), гранью не является, так как содержит
цикл (1, 2, 3,1). Простой цикл,
ограничивающий грань, называется границей грани. Две грани будем называть
соседними, если их границы имеют хотя бы одно общее ребро.
В данном графе часть плоскости,
ограниченная простым циклом (1,2,3,4,1), является
гранью, так как ребро (4,5), расположенное
внутри грани, не образует цикла.
Не является гранью заштрихованная
часть плоскости в данном примере, так как она содержит цикл, да к тому же эта
часть плоскости не ограничена циклом. Ребро (1,2) является
мостом, соединяющим циклы. Такие мосты называются перегородками.
В качестве грани можно
рассматривать и часть плоскости, расположенную «вне» плоского
представления графа. Она ограничена «изнутри» простым циклом и не
содержит других циклов. Эту часть плоскости называют бесконечной гранью.
На рисунке часть бесконечной грани
заштрихована. Всякое плоское представление графа либо не имеет бесконечной
грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится
бесконечная грань в плоском представлении дерева и леса. В плоском
представлении дерева и леса за грань принимают всю плоскость рисунка.
Два графа гомеоморфны (или
тождественны с точностью до вершин степени 2), если они оба могут быть получены
из одного и того же графа «включением» в его ребра новых вершин
степени 2.
Изображенные графы гомеомофны, и то же самое можно
сказать о любых двух циклических графах.
Гомеоморфность графов является отношением эквивалентности. Ясно, что введение термина
«гомеоморфны» удобно только с технической точки зрения — включение
или удаление вершин степени 2 не имеет никакого отношения к планарности.
Добавление (включение) одной вершины, скажем V,
в какое-нибудь ребро, например е, осуществляется
следующим образом: пусть ребро е инцидентно
вершинам w и х
. Тогда ребро е удаляется из графа,
но добавляются два новых ребра: е1инцидентное
вершинам V и w, и е2,
инцидентное вершинам V и x.
Введение понятия гомеоморфности графов позволяет установить следующий важный результат, известный как теорема Куратовского (точнее, как теорема Понтрягина-Куратовского, так как Л.С.Понтрягин доказал, но не опубликовал, эту теорему еще в 1927 году), которая дает необходимое и достаточное условие планарности графа.
Гомеоморфные графы
Теорема (Куратовский, 1930) Граф
планарен тогда и только тогда, если не содержит подграфов, гомеоморфных К5 или Кз,з.
Поскольку доказательство теоремы Куратовского
довольно длинное и сложное, здесь оно не приводится (см. Ф.Харари. Теория
графов. М.: «Мир». 1973). Тем не менее, воспользуемся теоремой
Куратовского для получения другого критерия планарности. Рассмотрим еще два
определения.
Элементарным
стягиванием называется такая процедура: берем ребро е (вместе с
инцидентными ему вершинами, например, V и W) и»стягиваем»
его, то есть удаляем е и отождествляем V и
W. Полученная при этом вершина инцидентна тем ребрам (отличным от
е ), которым первоначально были инцидентны V или W.
Граф G называется стягиваемым к графу Н,
если Н можно получить из G с помощью
некоторой последовательности элементарных стягиваний.
Граф планарен тогда и
только тогда, если он не содержит подграфов, стягиваемых в К5 или к Кз.з.
Формула Эйлера
Для всякого
плоского представления связного плоского графа без перегородок число вершин (V), число ребер (Е)
и число граней с учетом бесконечной (R) связаны
соотношением V –Е + R = 2.
Пусть граф G — связный, плоский граф без перегородок. Определим
значение алгебраической суммы V –Е + R для его произвольного плоского представления.
Преобразуем данный
граф в дерево, содержащее все его вершины. Для этого удалим некоторые ребра
графа G, разрывая поочередно все его
простые циклы, причем так, чтобы граф оставался связным и без перегородок.
Заметим, что при
таком удалении одного ребра число граней уменьшается на 1, так как при этом либо пропадет один простой цикл, либо два
простых цикла преобразуются в один. Следовательно, значение разности Е — R при этом остается неизменным.
На рисунке ребра,
которые мы удаляем, изображены кривыми. В полученном дереве обозначим число
вершин — Vd , число
ребер — Ed, число граней — Rd . Справедливо
равенство Е
— R
= Ed — Rd.
В дереве одна грань, то есть Е — R = Ed
— 1. Операция
удаления ребер из графа не меняет число его вершин, то есть V = Vd. По теореме в дереве Vd
— Ed = 1. Отсюда V — Ed = 1, то есть Ed
= V — 1, а потому Е-R = V — 2 или V — Е + R = 2.
Итак, доказано, что если в плоском
представлении связного графа без перегородок V вершин, Е ребер
и R граней,
то V — Е + R = 2. Полученная формула называется
формулой Эйлера.
Триангулированный граф
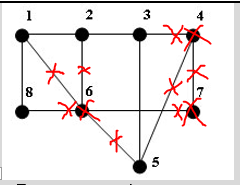
Рассмотрим плоский граф G с пятью вершинами.
Если добавить к нему ребра (1, 3) и (1,5) и, то полученный новый граф G тоже будет плоским.
К этому графу не удается добавить ни
одного ребра так, чтобы новый граф тоже был плоским.
Плоский граф называется максимально
плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный
граф был плоским. Изображенный граф является максимально плоским.
Каждая грань в плоском представлении
максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф
называют триангулированным. Операция
добавления новых ребер, в результате которой в плоском представлении каждая
грань имеет ровно 3 вершины, называется триангуляцией
графа.
Подграфы и деревья.
Подграфом графа G называется граф, у которого все вершины принадлежат
графу G.
Остовной связный подграф – это подграф графа G, который содержит все его вершины и
каждая его вершина достижима из любой другой.
Дерево — это граф, в котором нет циклов, то
есть граф, в котором нельзя из некоторой вершины пройти по нескольким различным
ребрам и вернуться в ту же вершину. Остовным связным деревом называется
подграф, включающий все вершины исходного графа G, каждая вершина которого достижима из
любой другой, и притом не содержащий циклов.
Преобразование графа
в остовное связное дерево минимального веса.
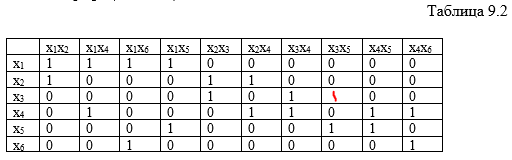
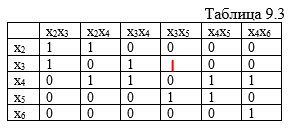
Пусть G = (V, R) – связный взвешенный неориентированный граф, где V — множество вершин, а R – множество
ребер. Ребра графа не ориентированы, то
есть ребра Rnk и Rkn считаются одним и тем же ребром, поэтому в матрице
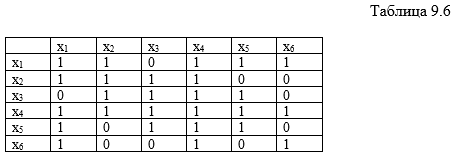
смежности не учитываются дублирующие друг друга ребра. В результате граф G можно представить с помощью матрицы
смежности, содержащей значения весов десяти ребер.
Введем понятие цикломатического числа y, показывающего, сколько ребер графа нужно удалить, чтобы в нем не
осталось ни одного цикла. Цикломатическое число y равно увеличенной на
единицу разности между количеством ребер и количеством вершин графа:
y = m – n +1, где m – количество ребер, n — количество
вершин.
Для каждого графа обычно существует несколько осотвных
связных деревьев, которые обладают различными весами.
Для построения остовного связного дерева минимального веса
используют алгоритм Крускала:
- Первоначально
из графа удаляются все ребра, получается остовной подграф, где все вершины
изолированы. Каждая вершина такого графа помещается в одноэлементное
подмножество. - Ребра
сортируются по возрастанию весов. - Ребра
последовательно, по возрастанию их весов, включаются в оставное дерево.
Существуют четыре случая:
а) обе вершины включаемого графа
принадлежат одноэлементным подмножествам, тогда они объединяются в новое,
связное подмножество.
б) одна из вершин принадлежит
связному подмножеству, а другая нет, тогда включаем вторую в подмножество,
которому принадлежит первая.
в) обе вершины принадлежат разным
связным подмножествам, тогда объединяем подмножества.
г) обе вершины принадлежат одному
связному подмножеству, тогда исключаем данное ребро.
4. Алгоритм заканчивает работу, когда все
вершины будут объединены ы одно множество, при этом оставшиеся ребра не
включаются в оставное дерево.
ПЗ
10. Графы (часть 2)
Инварианты
графа. Число вершин. Число ребер. Число
граней. Остовное дерево. Толщина.
Независимое множество. Клика и плотность
графа. Граф дополнения. Число доминирования.
9.1.
Инварианты графа
Два
графа называются изоморфными,
если у них одинаковое число вершин
(обозначим его n) и вершины каждого из
них можно занумеровать так числами от
1 до n, что в первом графе две вершины
соединены ребром тогда и только тогда,
когда вершины с такими же номерами во
втором графе соединены.
G1,
G2,
G3
– изоморфны.
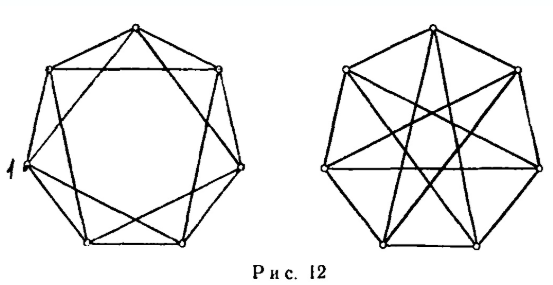
Рис.
9, 10, 11 – неизоморфны.
Рис.
12 – изоморфны
Рис.
13 – неизоморфны
|
G1
|
|
|
|
|
|
Рис. |
|
|
Какие
|
Степень
вершины
– 1)
для неорграфа количество инцидентных
к вершине ребер, петля учитывается
дважды: 2) для орграфа количество выходящих
ребер, петля учитывается единожды.
Инвариантом
графа
называется некоторая характеристика
графа G,
которая принимает одно и то е значение
для любого графа, изоморфного G.
Существуют
следующие инварианты графов
-
Количество
вершин n. -
Количество
ребер r. -
Количество
граней f. -
Число
связности k. -
Толщина
графа t(G). -
Плотность
графа q(G). -
Число
независимости
-
Число
вершинного покрытия
-
Число
паросочетания
. -
Число
реберного покрытия
. -
Число
доминирования
-
Хроматическое
число
-
Реберно-хроматическое
число
-
Коцикломатическое
число
-
Цикломатическое
число
Количество
граней можно найти для плоского связного
графа.
Плоский
граф
– граф, который укладывается на плоскости
так, что никакие два его ребра не
пересекаются нигде, кроме как в инцидентной
им обоим вершине.
Граф
называется связным,
если между любыми его вершинами существует
цепь.
Грань
– область плоскости, ограниченная
ребрами, любые две точки которой могут
быть соединены линией, не пересекающей
ребра графа.
Неограниченная
часть плоскости — тоже грань, так
называемая внешняя
грань.
Любой
граф можно разбить на подграфы, каждый
из которых окажется связным. Минимальное
число таких связных компонент называется
числом связности графа.
Толщина
графа
– минимальное количество его плоских
подграфов, при наложении которых
образуется исходный граф.
—
формула для поиска толщины графа.
Клика
– полный подграф графа G.
Количество
вершин максимальной клики графа
называется плотностью
графа.
Независимое
множество вершин
—
множество вершин графа, никакие две
вершины которого не инцидентны.
Максимальное
независимое множество вершин
—
независимое
множество вершин,
которое не содержится ни в каком другом
независимом
множестве вершин.
Наибольшее
независимое множество вершин
— независимое
множество вершин максимальной
мощности.
Независимое
множество ребер,
или паросочетание
— множество ребер графа, никакие два
ребра которого не инцидентны.
Мощность
наибольшего независимого
множества вершин называется
числом
независимости
графа (а также неплотностью,
числом
внутренней устойчивости или
числом
вершинной упаковки
графа).
Нахождение
наибольшего
независимого множества
(алгоритм):
1.
В графе выбрать вершину с наименьшей
степенью в качестве элемента исходного
множества.
2.
Удалить выбранную вершину из графа
вместе с ее окрестностью (смежные вершины
и инцидентные им ребра).
Шаги
1—2 повторять до тех пор, пока множество
вершин не станет пустым.
Доминирующее
множество вершин
—
такое множество вершин графа, что каждая
вершина графа либо принадлежит
доминирующему
множеству вершин,
либо инцидентна некоторой вершине из
него.
Число
доминирования графа.
Мощность наименьшего доминирующего
множества называется числом
доминирования
графа.
Для
решения задачи о нахождении числа
доминирования
графа применяется следующий алгоритм:
1.
Дополнить матрицу смежности единицами
по главной диагонали.
2.
Выбрать из матрицы смежности строку с
наибольшим числом единиц и ввести ее в
искомое покрытие.
3.
Вычеркнуть строку из матрицы и столбцы,
покрываемые этой строкой.
Повторять
шаги 2 и 3 до тех пор, пока в матрице
множество столбцов не окажется пустым.
Алгоритм
поиска наибольшего паросочетания:
1.
Выбираем ребро с наименьшей степенью
(число инцидентных вершин) и включаем
в искомое паросочетание. Если таковых
несколько, выбираем то из них, для
которого степень второй граничной
вершины наименьшая.
2.
Удаляем из графа это ребро и ребра,
смежные с ним.
Шаги
1—2 повторять до тех пор, пока множество
ребер не станет пустым.
|
Задача
|
Предположим, что футбольная команда вашей школы участвует в соревнованиях и играет с командами других школ. Пусть общее число команд равно шести. Вашу команду обозначим буквой А, а другие команды — буквами B, C, D, E и F. Через несколько недель после начала соревнований окажется, что некоторые из команд уже сыграли друг с другом, например:
A с C, D, F;
B c C, E, F;
С с A, B;
D с A, E, F;
E с B, D, F;
F с A, B, D.
Это можно изобразить при помощи такой геометрической схемы. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом. Тогда для данного списка проведенных игр мы получим схему, изображенную на рис. 5.
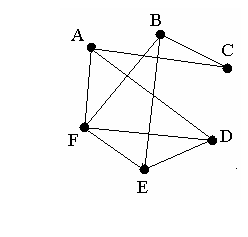
рис. 1
Схема такого вида называется графом. Она состоит из нескольких точек А, В, С, D, E, F,называемых вершинами, и нескольких соединяющих эти точки отрезков, таких, как АС или ЕВ, называемых ребрами графа.
Итак, фигуру, образованную набором точек и отрезков, соединяющих некоторые из этих точек, называется графом. Точки называются вершинами графа. А отрезки – ребрами графа.
Примерами графов могут служить схемы метрополитена, железных и шоссейных дорог, планы выставок и т.д. С помощью графов указываются различные связи между объектами.
Из рис. 5 видно, что точки пересечения некоторых ребер графа могут не являться его вершинами; это происходит потому, что мы изобразили наш граф на плоскости. Возможно, удобнее было бы представлять себе его ребра нитями, проходящими друг над другом в пространстве; во всяком случае, при изображении на плоскости вершины графа во избежание путаницы должны отмечаться достаточно отчетливо (например, кружочками).
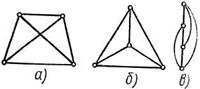
Один и тот же граф может выглядеть на рисунках по-разному. Например, на трех рисунке 6 (а), (б), (в), мало похожих друг на друга, изображен один и тот же граф. Три этих графа имеют одинаковое число вершин, и соответствующие вершины графов соединены ребрами.
рис. 6
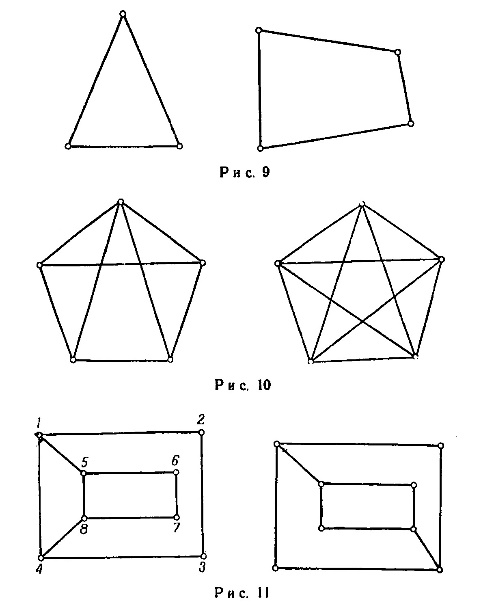
Задача 1.1. Рассмотрим следующие рисунки. Изображают ли они один и тот же граф?
А)
1. Проверим число вершин на графах.
В первом графе три вершины, а во втором четыре, следовательно, графы разные.
B)
1. Проверим число вершин на графах.
В первом и во втором графе по четыре вершины.
2. Проверим, соединены ли ребрами соответствующие вершины графа.
Вершина А в первом графе соединена только с вершиной В. А во втором графе вершина А соединена еще и с вершиной D. Следовательно графы разные.
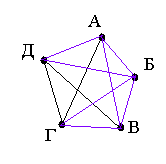
Задача 1.2. Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
Решение:
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию – отрезок или часть кривой, соединяющая конкретные точки – имена.
Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.
1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рис 3. Такую схему называют нулевым графом.
Рис 9. Рис 10.
2. Ситуация, соответствующая моменту, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рис. 10.
Графы, в которых построены не все возможные ребра, называются неполными графами.
3. На рис. 9 Борис не сделал ни одного рукопожатия. Вершины, которые не принадлежат ни одному ребру, называются изолированными.
Теперь мы можем тать четкое определение нулевому графу. Схема, состоящая из «изолированных» вершин, называется нулевым графом.
4. Ситуация, когда осуществились все рукопожатия, изображена на рис. 11. В нем каждая из вершин соединена с каждой из оставшихся. Этот граф называется полным графом.
Рис 11.
Если мы подсчитаем число ребер графа, изображенного на рис. 11, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Заметим, что граф, не являющийся полным, можно дополнить до полного с теми же вершинами, добавив недостающие ребра. Так на рис. 10 изображен неполный граф с пятью вершинами. А на рис. 11 граф превращен в полный. Ребра, превращающие граф в полный изображены фиолетовым цветом. Совокупность вершин графа с этими ребрами называется дополнением графа.
Предложение 1. Докажем, что если полный граф имеет n вершин, то количество ребер будет равно: .
Действительно, всего вершин n штук, каждая соединена с n-1 вершиной – получаем произведение n(n-1). Но мы посчитали каждое ребро два раза, значит, надо произведение разделить на два, и тогда получим искомую формулу для нахождения количества ребер.
Задача 1.3. Существует ли полный граф с семью ребрами?
Решение. Допустим, что такой граф существует.
Зная количество ребер, узнаем количество вершин.
=7; n(n-1)=14.
Заметим, что n и (n-1) – это два последовательных натуральных числа. Число 14 не6льзя представить в виде произведения двух последовательных натуральных чисел, значит, данное уравнение не имеет решений. Следовательно, такого графа не существует.
Готовимся к олимпиаде. Теория графов (НАЧАЛО)
Граф — это конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие их линии — рёбрами. Каждое ребро соединяет ровно две различные вершины.
Пример. Транспортный граф.
В стране есть пять городов: А, В, С, D и Е. Дороги соединяют следующие пары городов: А и В, В и С, В и D, C и D, D и E.
Это можно изобразить в виде следующего графа:

Иногда графы бывает удобно задавать перечислением множества вершин и множества рёбер.
Например, граф на рисунке выше можно задать следующим образом: это граф c вершинами {A, B, C, D, E} и рёбрами {AB, BC, BD, CD, DE}.
Пример. Социальный граф.
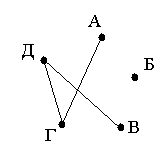
Андрей, Вася, Саша, Дима и Евгений отправились в поход. До начала похода Андрей был знаком с Васей, Сашей и Димой, а Саша — с Димой, другие ребята не были знакомы между собой.
Это можно изобразить в виде следующего графа:

Пример. Турнирный граф.
В школе между пятью классами проходил однокруговой турнир по футболу. К середине марта три класса сыграли все матчи между собой, а оставшиеся два класса не сыграли ни одного матча. К середине апреля все матчи были сыграны.
Это можно изобразить в виде следующих графов:

Можно привести и другие примеры, когда графы возникают естественным образом: граф авиасообщений, генеалогическое древо.
Полный граф — это граф, в котором каждые две вершины соединены ребром.

Степень вершины — это количество рёбер, концом которых является эта вершина.
Посчитаем степени вершин на примере следующих графов.
Степень вершины А равна 1.
Степень вершины В равна 3.
Степень вершины С равна 2.
Степень вершины D равна 3.
Степень вершины Е равна 1.

Степень вершины «Андрей» равна 3.
Степень вершины «Вася» равна 1.
Степень вершины «Саша» равна 2.
Степень вершины «Дима» равна 2.
Степень вершины «Евгений» равна 0.

Изолированная вершина — это вершина графа, степень которой равна нулю.
Утверждение.
Количество рёбер (обозначается Е) в графе равно половине суммы степеней всех его вершин.
Пример. На данном графе Е = (1 + 3 + 2 + 3 + 1) : 2 = 5.

Задача 1. (Подсчёт количества рёбер по известным степеням вершин.)
В однокруговом футбольном турнире участвовали шесть команд. К середине турнира оказалось, что четыре команды сыграли по два матча, а две оставшиеся команды сыграли по одному матчу. Сколько матчей было сыграно к середине турнира?
РЕШЕНИЕ.
Команды – это вершины графа, а количество сыгранных матчей – это степени вершин (количество исходящих из них рёбер).
Тогда у нас имеется 4 вершины степени 2 и 2 вершины степени 1.
Требуется найти количество сыгранных матчей, т.е. количество рёбер графа.
Е = (4 ∙ 2 + 2 ∙ 1) : 2 = 10 : 2 = 5.
ОТВЕТ: 5 матчей.
ЗАДАЧА 2. (Поиск степени вершины по известным степеням остальных вершин и количеству рёбер.)
В государстве есть 21 город: 10 малых городов, 10 средних городов и столица. Между городами построено 25 дорог. Известно, что из каждого малого города выходит ровно по одной дороге, а из каждого среднего — ровно по две. Сколько дорог может выходить из столицы?
РЕШЕНИЕ.
Города – это вершины графа, а количество дорог – это степени вершин (количество исходящих из них рёбер).
Тогда у нас имеется:
10 вершин степени 1,
10 вершин степени 2,
1 вершина (столица) степени х.
Всего имеется 25 дорог, т.е. общее количество рёбер Е = 25.
Требуется найти количество дорог, выходящих из столицы, т.е. найти х.
Составим и решим уравнение:
(10 ∙ 1 + 10 ∙ 2 + 1 ∙ х) : 2 = 25.
(10 + 20 + х) : 2 = 25,
30 + х = 50,
х = 20.
ОТВЕТ: 20 дорог.
ЗАДАЧА 3. (Поиск степени вершины по известным степеням остальных вершин и количеству рёбер.)
Дядька Черномор и 33 богатыря в течение 50 дней каждый день отправляли двух человек патрулировать берег моря (либо двух богатырей, либо дядьку Черномора вместе с одним богатырём). Известно, что никакая пара людей не дежурила дважды. Могло ли так оказаться, что каждый богатырь дежурил ровно два раза?
РЕШЕНИЕ.
У нашего графа имеется 34 вершины – 33 богатыря и Дядька Черномор.
А что будет служить рёбрами? Когда 2 человека идут вместе дежурить, соответствующие им вершины будем соединять рёбрами.
Так как было 50 дежурств, значит, в графе будет 50 рёбер.
Могло ли оказаться, что каждый богатырь продежурил 2 раза? На языке графов это звучит так: могло ли оказаться, что степени 33 вершин будут равны 2?
Итак, пусть имеется:
33 вершины – степени 2,
1 вершина (Черномор) – степени х.
Всего – 50 рёбер.
Составим и решим уравнение:
(33 ∙ 2 + 1 ∙ х) : 2 = 50,
66 + х = 100,
х = 34.
Получается, что Дядька Черномор дежурил на берегу 34 дня, причём каждый раз с разными людьми. Но богатырей только 33. По принципу Дирихле это невозможно.
Значит, каждый богатырь дежурить по 2 раза не мог.
ОТВЕТ: нет.
ЗАДАЧА 4. (Поиск суммы степеней двух вершин по известным степеням остальных вершин и количеству рёбер.)
В графе семь вершин и семь рёбер. Известно, что у каких-то двух его вершин степень 2, а у каких-то трёх — степень 3. Докажите, что в этом графе есть изолированная вершина.
РЕШЕНИЕ.
У нашего графа имеется 7 вершин и 7 рёбер.
Кроме того, имеется:
2 вершины – степени 2,
3 вершины – степени 3.
Но это только 2 + 3 = 5 вершин. А что можно сказать про оставшиеся 2 вершины графа?
Пусть:
1 вершина – степени х,
1 вершина – степени у.
Составим уравнение:
(2 ∙ 2 + 3 ∙ 3 + 1 ∙ х + 1 ∙ у) : 2 = 7,
(13 + х + у) : 2 = 7,
13 + х + у = 14,
х + у = 1.
Но ведь х и у – это степени вершин, значит, они могут принимать только целые положительные значения.
Но тогда хотя бы одно из них равно 0 – либо х = 0, либо у = 0.
Значит, в графе есть изолированная вершина (у которой степень равна нулю).
Что и требовалось доказать.
Лемма.
В любом графе сумма степеней его вершин чётна.
Лемма о рукопожатиях.
В любом графе количество вершин нечётной степени чётно.
Лемма о рукопожатиях является необходимым условием существования графа, но не достаточным.
Ссылка на видеоресурс по данной теме:
ЗАДАЧА 5.
В шахматный клуб пришли 7 человек, они сыграли между собой несколько партий. Могло ли так оказаться, что каждый из них сыграл ровно 3 партии? Каждую партию играют два человека.
РЕШЕНИЕ.
Первый способ.
Пусть 7 человек – это 7 вершин графа. И пусть каждый из них сыграл 3 партии.
Тогда у нас имеется 7 вершин (нечётное число) степени 3 (нечётная степень). То есть граф составлен нечётным числом вершин нечётных степеней. Это противоречит лемме о рукопожатиях.
Второй способ.
Допустим, что каждый из 7 человек сыграл по 3 партии. Тогда мы имеем граф с 7 вершинами степени 3.
7 вершин – со степенью 3.
Тогда количество рёбер в графе равно:
Е = (7 ∙ 3) : 2 = 10,5 – нецелое число рёбер.
Но количество рёбер должно быть целым. Значит, 7 человек по 3 партии сыграть не могли.
ОТВЕТ: нет.
ЗАДАЧА 6.
Архипелаг состоит из 20 островов, между некоторыми из которых построены мосты. Могло ли так оказаться, что из пяти островов выходит по 3 моста, из семи островов — по 4 моста, а из восьми островов — по 5 мостов?
РЕШЕНИЕ.
20 островов – это 20 вершин графа.
У этого графа имеется:
5 вершин – степени 3,
7 вершин – степени 4,
8 вершин – степени 5.
Первый способ.
По лемме о рукопожатиях количество вершин с нечётными степенями должно быть числом чётным.
А у нас таких вершин 5 + 8 = 13 – нечётное число.
Значит, это невозможно.
Второй способ.
Посчитаем количество рёбер этого графа:
Е = (5 ∙ 3 + 7 ∙ 4 + 8 ∙ 5 ) : 2 = 83 : 2 = 41,5 – нецелое количество рёбер в графе.
Но такого быть не может, т.к. число рёбер должно быть целым.
ОТВЕТ: нет.
ЗАДАЧА 7.
В деревне 10 домов, и из каждого выходит по 7 тропинок, идущих к другим домам. Сколько всего тропинок проходит между домами?
РЕШЕНИЕ.
Пусть дома – это вершины графа, а тропинки – это рёбра графа. Тогда имеем 10 вершин со степенью 7.
Сумма степеней равна 10 ∙ 7 = 70. Значит, количество рёбер Е = 70 : 2 = 35.
ОТВЕТ: 35 тропинок.
ЗАДАЧА 8.
Между 7 планетами звёздной системы установлено ракетное сообщение. Министр отрапортовал, что с каждой планеты существует прямой рейс ровно на 5 других планет системы. Докажите, что министр ошибся.
РЕШЕНИЕ.
Пусть планеты – это вершины графа, а маршруты – это его рёбра. Тогда в нашем графе 7 вершин со степенью 5.
Если министр прав, то сумма степеней вершин графа равна 7 ∙ 5 = 35. Но сумма степеней вершин любого графа должна быть чётной, т.к. в противном случае количество рёбер равно:
Е = 35 : 2 = 17, 5 – нецелое число маршрутов.
Поскольку количество рёбер показывает количество маршрутов, то это число должно быть целым.
Значит, министр ошибся.
Что и требовалось доказать.