Сколько вершин имеет правильный многоугольник, если каждый его угол=156 градусов?
Сколько вершин имеет правильный многоугольник, если каждый его угол=156 градусов? можете полностьЮ расписать и объяснить ответ?
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.
Для выпуклого n-угольника сумма углов равна 180°(n-2)
180(n-2)=156n
180n-360=156n
180n-156n=360
24n=360
n=15
ОТВЕТ: 15 вершин
Как найти число вершин многоугольника
Тип 3 № 54114
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 170°. Найдите число вершин многоугольника.
Это задание ещё не решено, приводим решение прототипа.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108°. Найдите число вершин многоугольника.
Сумма углов n-угольника равна 180°(n − 2). Каждый из них равен 108°, поэтому, с другой стороны, эта сумма равна 108°n. Решим уравнение 180°(n − 2) = 108°n. Получим 72°n = 360°, откуда n = 5. Таким образом, многоугольник имеет 5 вершин.
Приведём другое решение.
Рассмотрим равнобедренный треугольник AOB, где А и B — соседние вершины многоугольника, О — центр окружности (см. рис.). Углы при основании треугольника равны равны 54°, следовательно, угол при вершине равен 72°. Тогда n = 360° : 72° = 5. Таким образом, многоугольник имеет 5 вершин.
Решение №2071 Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.
Решение:
В правильном многоугольнике все углы равны. Пусть n – количество углов и вершин. Тогда сумму углов многоугольника можно найти как:
n·168
Или по формуле суммы углов выпуклого n-угольника:
180·(n – 2)
Приравняем и найдём n:
n·168 = 180·(n-2)
n·168 = 180·n-2·180
360 = 180·n – 168·n
360 = 12n
n = 360/12 = 30
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.
Источник: mathege
Решение:
В правильном многоугольнике все углы равны. Пусть n – количество углов и вершин. Тогда сумму углов многоугольника можно найти как:
n·168
Или по формуле суммы углов выпуклого n-угольника:
180·(n – 2)
Приравняем и найдём n:
n·168 = 180·(n-2)
n·168 = 180·n-2·180
360 = 180·n – 168·n
360 = 12n
n = 360/12 = 30
Ответ: 30.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 16
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
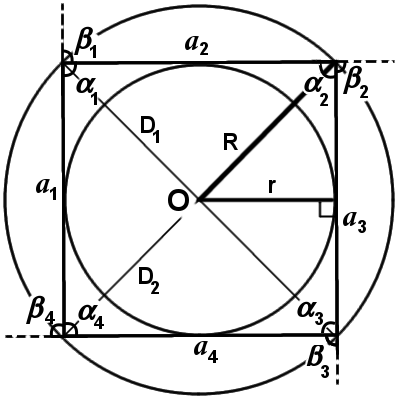
Основные свойства правильного многоугольника
1. Все стороны равны:
a1 = a2 = a3 = … = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
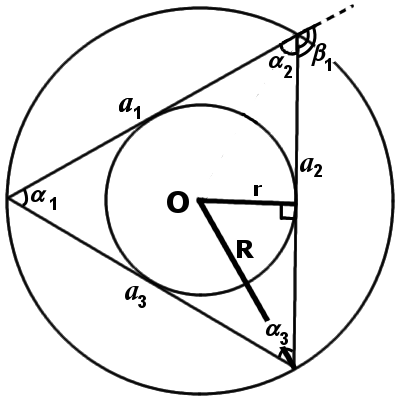
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
2. Формула площади n-угольника через радиус вписанной окружности:
3. Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
 |
| Рис.3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
α = 135°

Вам сюда —
http://www.genon.ru/GetAnswer.aspx?qid= … e4230f59fb
Диагональ в многоугольнике (многограннике) — отрезок, соединяющий любые две несмежные вершины, то есть, вершины, не принадлежащие одной стороне многоугольника (одному ребру многогранника).
У многогранников различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за пределы граней. У многогранников, имеющих треугольные грани есть только пространственные диагонали.
Подсчет диагоналей
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника легко вычислить по формуле:
N = n*(n – 3)/2,
где n — число вершин многоугольника. По этой формуле нетрудно найти, что
у треугольника — 0 диагоналей
у прямоугольника — 2 диагонали
у пятиугольника — 5 диагоналей
у шестиугольника — 9 диагоналей
у восьмиугольника — 20 диагоналей
у 12-угольника — 54 диагонали
у 24-угольника — 252 диагонали
Количество диагоналей многогранника с числом вершин n легко подсчитать только для случая, когда в каждой вершине многогранника сходится одинаковое число ребер k. Тогда можно пользоваться формулой:
N = n*(n – k – 1)/2,
которая даем сумманое число пространственных и граневых диагоналей. Отсюда можно найти, что
у тетраэдра (n=4, k=3) — 0 диагоналей
у октаэдра (n=6, k=4) — 3 диагонали (все пространственные)
у куба (n=8, k=3) — 16 диагоналей (12 граневых и 4 пространственных)
у икосаэдра (n=12, k=5) — 36 диагоналей (все пространственные)
у додекаэдра (n=20, k=3) — 160 диагоналей (25 граневых и 135 пространственных)
Если в разных вершинах многогранника сходится разное число ребер, подсчет заметно усложняется и должен проводится индивидуально для каждого случая.
Фигуры с равными диагоналями
На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой. Это квадрат и правильный пятиугольник. У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом. У правильного пятиугольника пять одинаковых диагоналей, которые вместе образуют рисунок пятиконечной звезды (пентаграммы).
Единственный правильный многогранник, у которого все диагонали равны между собой — правильный восьмигранник октаэдр. У него три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра — пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).
Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой. Это куб (гексаэдр). У куба четыре одинаковых пространственных диагонали, которые также пересекаются в центре. Угол между дигоналями куба состаляет либо arccos(1/3) ≈ 70,5° (для пары диагоналей, проведенных к смежным вершинам), либо arccos(–1/3) ≈ 109,5° (для пары диагоналей, проведенных к несмежным вершинам).
Ссылки:
ru.wikipedia.org — Википедия: Диагональ
dic.academic.ru — иллюстрация разницы между граневой и пространственной диагоналями многогранника
Дополнительно в базе данных Генона:
Как найти диагональ прямоугольника?
Сколько вершин, ребер и граней у тетраэдра?
Сколько вершин, ребер и граней у куба (гексаэдра)?
Правильный многоугольник это выпуклый многоугольник, у которого равны все стороны и углы между смежными сторонами тоже равны. Для расчета правильного многоугольника введите длину ребра и количество вершин. Затем нажмите кнопку вычислить. Так же может быть вычислена длинна диагоналей по длине ребра. Углы р отображаются в градусах.
.
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Диагональ между вершинами
Формулы:
n ∈ ℕ, N > 2>
p = a * n
h = 2 * r, Если n четно, иначе
h = a / (2 * tan (π / 2/n ) )
S = n * a2 / (4 * tan (π/n) )
R = a / (2 * sin (π/n) )
r = a / (2 * tan (π/n) )
Угол = 180° — 360° / n
d = n ( n-3 ) / 2
Диагональ через M ребер, m ∈ ℕ, m ≤ n/2:
dm = a * sin( π * m/n) / sin( π/n)
Если вам нужно рассчитать правильный многоугольник с вырезом по центру.

