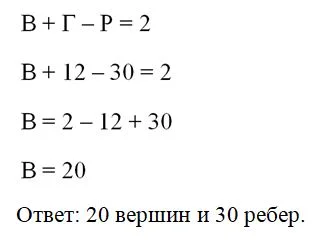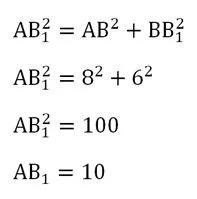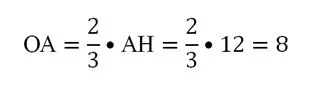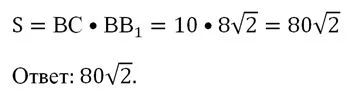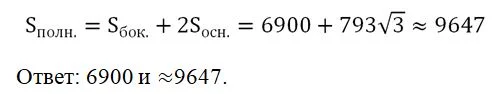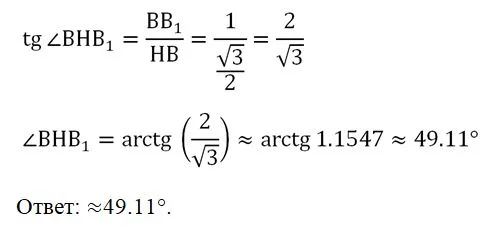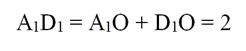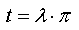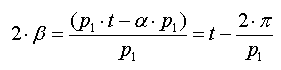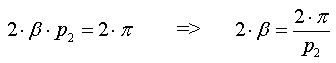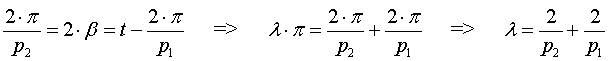Как найти количество вершин в многограннике

План урока:

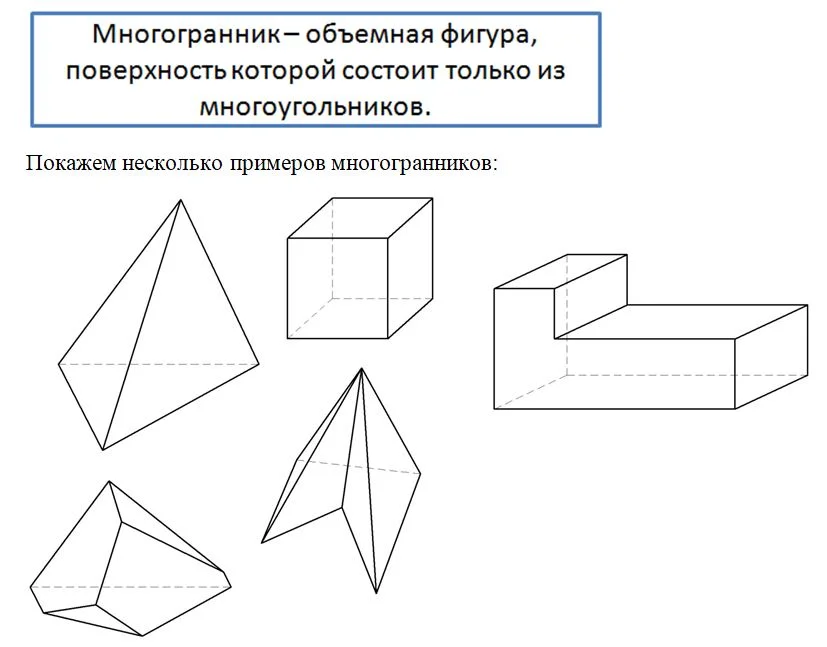
Понятие многогранника

Теорема Эйлера

Призма

Типичные задачи на призмы

Понятие многогранника

Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.

Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».

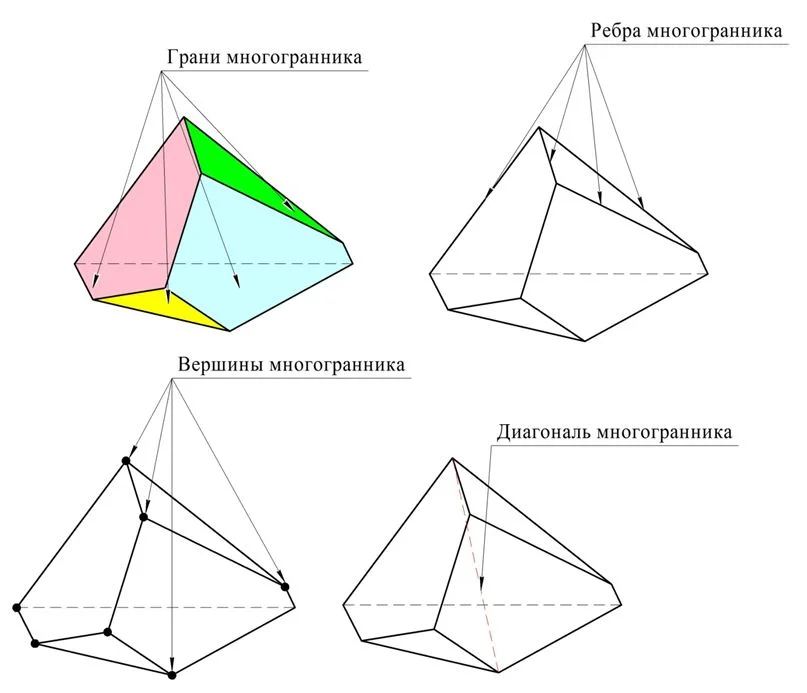
Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.

Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника. Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу.

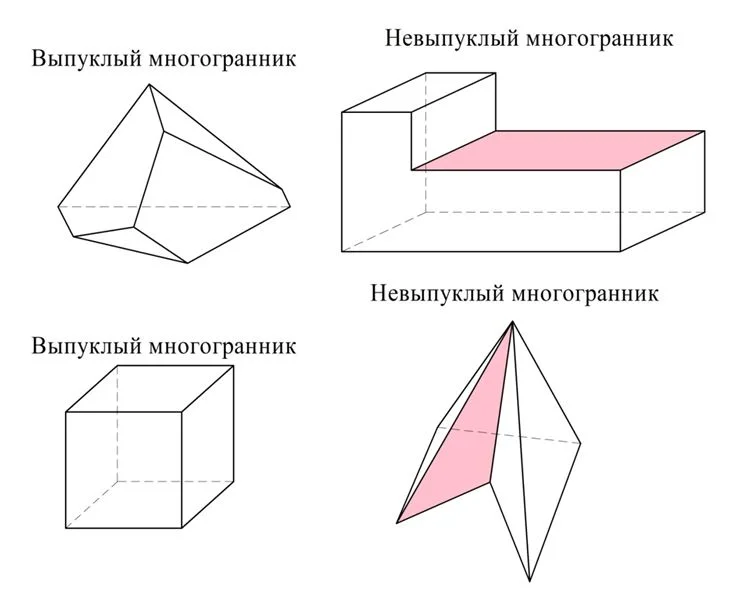
Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:

На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.

Теорема Эйлера

У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?

Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:

4 + 4 — 6 = 2

Если выполнить такие же действия для параллелепипеда, то снова получится двойка:

6 + 8 — 12 = 2

Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:

Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.

Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?

Решение. Запишем теорему Эйлера:

Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?

Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:

Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?

Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:

Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?

Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:

Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:

Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.

Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.

Призма

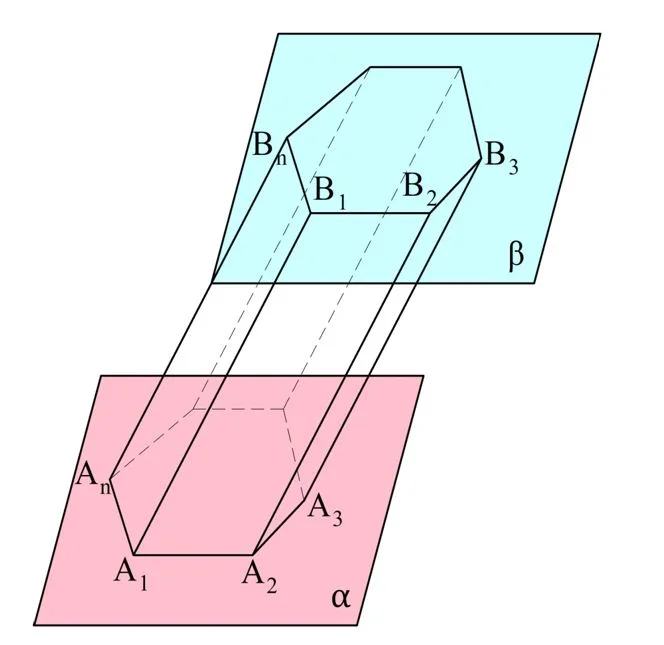
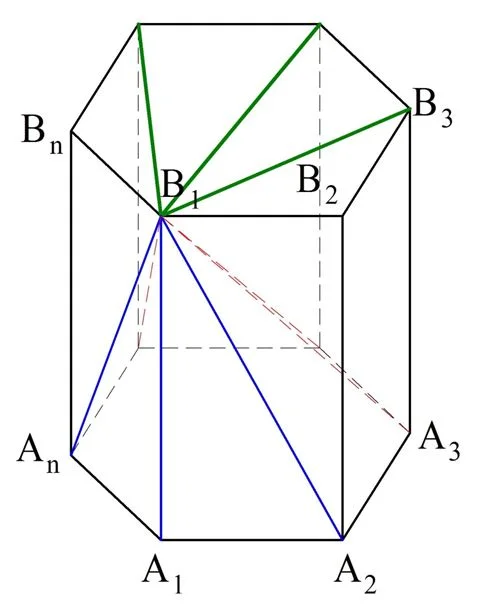
Пусть в некоторой плос-ти α есть n-угольник с вершинами А₁, А₂, А₃,…, А_n. Пусть в другой плос-ти β, которая параллельна α, есть равный ему многоуг-к В₁В₂В₃…В_n, причем отрезки А₁В₁, А₂В₂, А₃В₃…, А_nВ_n параллельны друг другу:

В результате мы получили геометрическую фигуру, которую именуют призмой. Многоуг-ки А₁А₂А₃…А_n и В₁В₂В₃…В_n именуются основаниями призмы, а все остальные грани – это боковые грани призмы. Можно доказать, что боковые грани – это параллелограммы. Действительно, в четырехуг-ке А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию. Также они равны по теореме 12 из этого урока. Это и значит, что А₁А₂В₂В₁ – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:

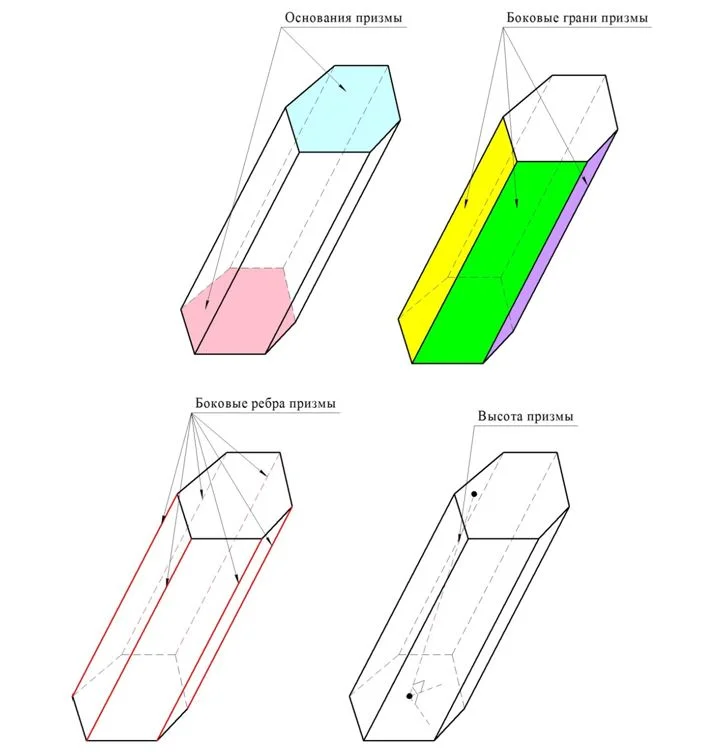
Ребра призмы, не принадлежащие основанию, именуются боковыми ребрами призмы. Ясно, что любые два соседних ребра параллельны, ведь они являются сторонами параллелограммами. Но тогда по свойству транзитивности параллельности получается, что вообще любые два боковых ребра параллельны. Если из какой-нибудь точки основания построен перпендикуляр к противоположному основанию, то он именуется высотой призмы:

Естественно, что высота перпендикулярна обоим основаниям. Возможна ситуация, когда высота падает не на основание, а на какую-нибудь точку плос-ти основания, не находящуюся внутри него. Ясно, что все высоты призмы имеют одинаковую длину независимо от того, через какие точки они проведены, ведь высота по своей сути – это расстояние между плос-тями оснований.

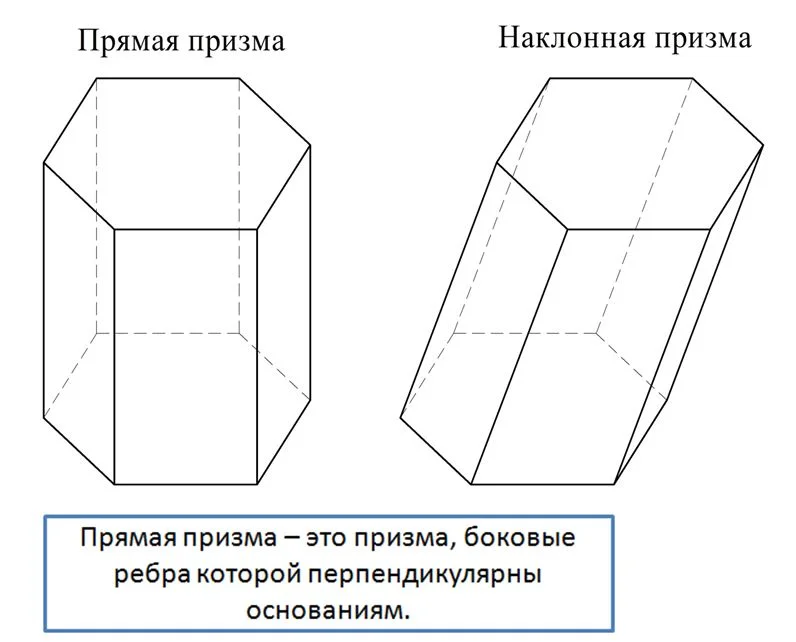
Особый интерес вызывают призмы, где боковые ребра и основания перпендикулярны друг другу. Такие призмы именуются прямыми. Ясно, что у них боковые грани оказываются уже не просто параллелограммами, а уже прямоуг-ками. При этом любое боковое ребро одновременно является и высотой. Все остальные призмы именуют наклонными.

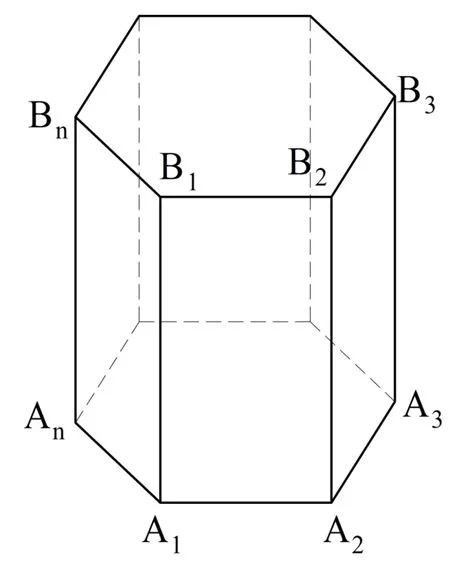
Если в основании призмы находится n-угольник, то призму называют n-угольной. В частности, в основании треугольной призмы лежит треуг-к, в основании десятиугольной призмы находится десятиугольник и т. д. Наконец, в особую группу выделяют прямые призмы, основаниями которых представляют собой правильные многоуг-ки. Их так и именуют – правильные призмы.

Если сложить площадь всех граней призмы, то получится сумма, которую именуют площадью полной поверхности призмы. Обычно ее обозначают как S_полн. Если же складываются только площади боковых граней, то в сумме получается площадь боковой поверхности призмы, обозначаемая как S_бок. Если площадь основания призмы обозначить как S_осн., то справедлива будет очевидная формула:

Действительно, пусть есть прямая призма с основаниями А₁А₂…А_n и B₁B₂…B_n:

Так как ее боковые ребра перпендикулярны основаниям, то они должны быть перпендикулярны и тем ребрам, которые образуют основания. Это значит, каждая боковая грань – это прямоуг-к. При этом боковые ребра – это одновременно и высоты призмы. Тогда площадь боковых граней вычисляется так:

Отметим наконец, что параллелепипед можно считать частным случаем призмы, а прямоугольный параллелепипед – частным случаем прямой призмы.

Типичные задачи на призмы

Призмы нередко встречаются в заданиях ЕГЭ, поэтому важно уметь решать задачи, в которых используются эти фигуры.

Задание. Сколько диагоналей имеет n-угольная призма?

Решение. В любом многограннике диагональ соединяет точки, не лежащие на одной грани. Каждая вершина призмы принадлежит одному из оснований, причем в n-угольной призме каждому основанию принадлежат n вершин.

Возьмем произвольную вершину на одном из оснований и посчитаем, сколько диагоналей из нее можно провести. Если соединять ее отрезками с другими вершинами, принадлежащему тому же основанию, то получатся диагонали грани, но не диагонали призмы (зеленые линии на рисунке):

Значит, остается только провести прямые к тем вершинами, которые лежат в другом основании. Так как в другом основании находятся n вершин, то и отрезков будет ровно n. Однако три из них не будут диагоналями (показаны на рисунке синим цветом), так как будут либо являться одним из ребер призмы либо одной из диагоналей. Получается, что из вершины можно провести (n – 3) диагоналей. Так как в основании находятся n вершин, то всего можно построить n•(n– 3) диагоналей.

Ответ: n•(n – 3) диагоналей.

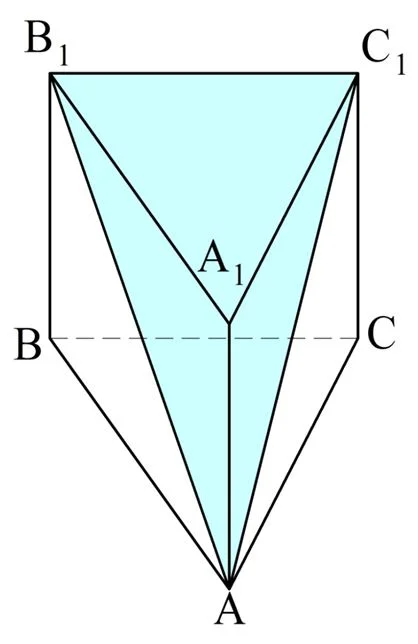
Задание. Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?

Решение. Выполним построение по условию задачи:

Здесь сечение проведено через ребро В₁С₁ и противолежащую ей вершину А. Призма правильная, поэтому ее основания ∆АВС и ∆А₁В₁С₁ – это равносторонние треуг-ки, и все их стороны равны 8 см. По определению правильная призма обязательно ещё и прямая. Тогда боковые грани – прямоуг-ки.

∆АВВ₁ – прямоугольный, с помощью теоремы Пифагора мы можем вычислить его гипотенузу АВ₁:

Аналогично можно вычислить, что и диагональ АС₁ также равна 10 см. Вообще в правильных призмах все грани – это равные друг другу прямоуг-ки, поэтому и диагонали у них одинаковы.

Длина ребра В₁С₁ составляет 8 см. Получается, нам надо вычислить площадь равнобедренного ∆АВ₁С₁ с основанием 8 см и боковыми сторонами 10 см. Это можно сделать множеством способов. Самый простой из них заключается в использовании формулы Герона. Для ее применения сначала вычислим полупериметр ∆АВ₁С₁:

Задание. В основании призмы находится равносторонний ∆АВС. Ребро АА₁ образует одинаковые углы с ребрами АС и АВ. Докажите, что ребра АА₁ и ВС перпендикулярны и что СС₁В₁В – прямоуг-к.

Решение. Выполняем построение:

По условию ∠А₁АВ и ∠А₁АС одинаковы. Проведем диагонали А₁В и А₁С. В итоге мы получим ∆А₁АВ и А₁АС. У них есть АА₁ – общая сторона, стороны АВ и АС одинаковы (ведь ∆АВС – равносторонний), а углы между ними одинаковы. Значит, ∆А₁АВ и А₁АС равны, и тогда диагонали А₁В и А₁С одинаковы.

Получается, что точка А₁ равноудалена вершин В и С. Аналогично и точка А равноудалена от В и С, ведь АВ и АС одинаковы. Это значит, что и А₁, и А лежат на серединных перпендикулярах, проведенных к отрезку ВС:

Обозначим середину ВС как Н, тогда НА₁ и НА – серединные перпендикулярны. То есть ВС⊥АН и ВС⊥А₁Н. Но это значит (по признаку перпендикулярности прямой и плос-ти), что ВС перпендикулярен всей плос-ти АНА₁. Из этого вытекает, что ВС⊥АА₁, ч. т. д.

Осталось показать, что грань СС₁В₁В – это прямоуг-к. Так как ВВ₁||АА₁, и ВС⊥АА₁, то и ВС⊥ВВ₁. Значит в параллелограмме СС₁В₁В (напомним, что в призме все боковые грани – параллелограммы) есть прямой угол. Это значит, что он является прямоуг-ком, ч. т. д.

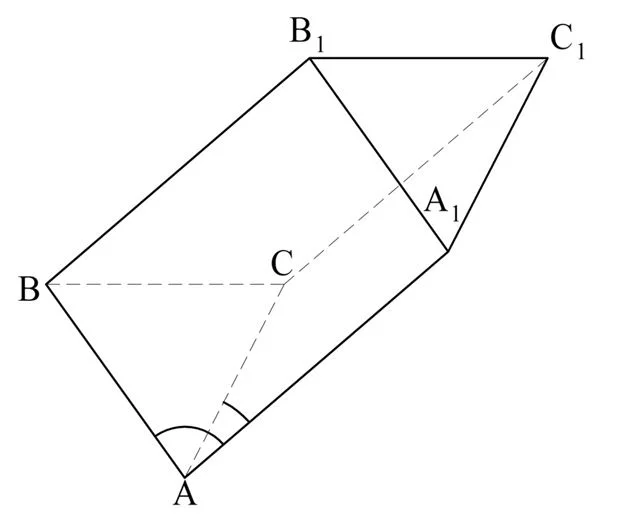
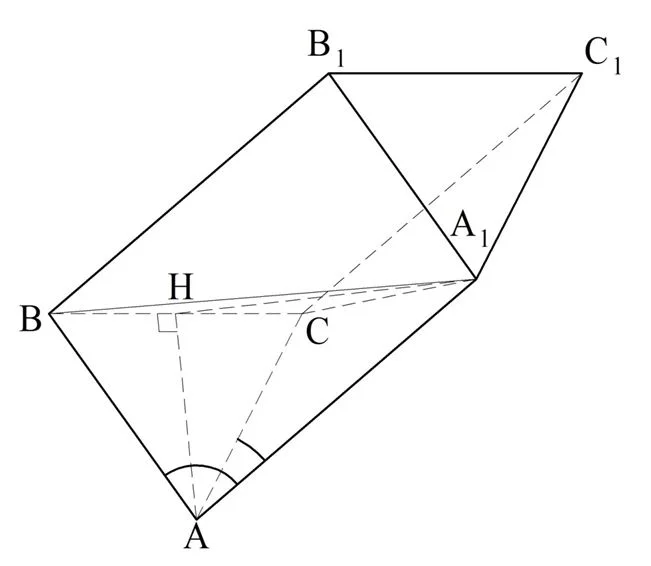
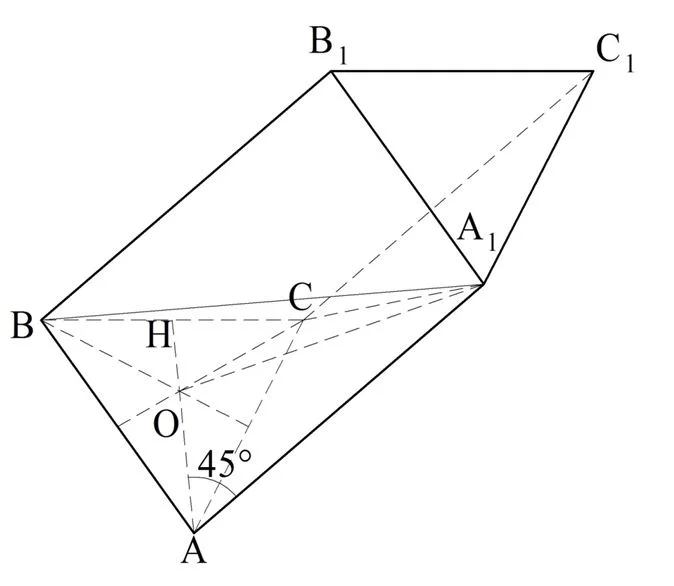
Задание. Призма АВСА₁В₁С₁ – наклонная. Известно, что АС = АВ = 13 и ВС = 10. Боковые ребра призмы образуют с основанием АВС угол 45°. Проекция точки А₁ на плос-ть АВС совпадает с точкой пересечения медиан в ∆АВС. Какова площадь грани СС₁В₁В?

Решение. Снова выполняем построение:

Здесь О – это проекция точки А₁ и одновременно точка пересечения медиан. H– середина отрезка ВС, то есть АН – как раз одна из медиан. Заметим, что так как ∆АВС равнобедренный, и ВС – это его основание, то АН одновременно является и высотой, то есть ∠ВНА = 90°. Раз Н – середина ВС, то ВН будет вдвое короче ВС:

Напомним, точка пересечения медиан делит их в отношении 2:1, поэтому мы можем найти ОА:

Понятно, что ОА – это проекция прямой ОА на плос-ть АВС. Тогда угол между ребром АА₁ и плос-тью АВС, по условию равный 45° – это ∠ОАА₁.

Из прямоугольного ∆АОА₁ с помощью тригонометрии мы найдем длину ребра АА₁:

Теперь покажем, что грань СС₁В₁В – прямоуг-к. Ясно, что ОА₁⊥ВН, ведь ОА₁ – перпендикуляр ко всей плос-ти АВС. Но также ВН⊥АН. Значит, ВН перпендикулярен плос-ти АОА₁, и, в частности, перпендикулярен ребру АА₁. Но тогда и ВВ₁⊥ВН, ведь ВВ₁||АА₁. Значит, грань СС₁В₁В – прямоуг-к, ведь в ней есть прямой угол. Для нахождения площади прямоуг-ка надо перемножить две его смежные стороны:

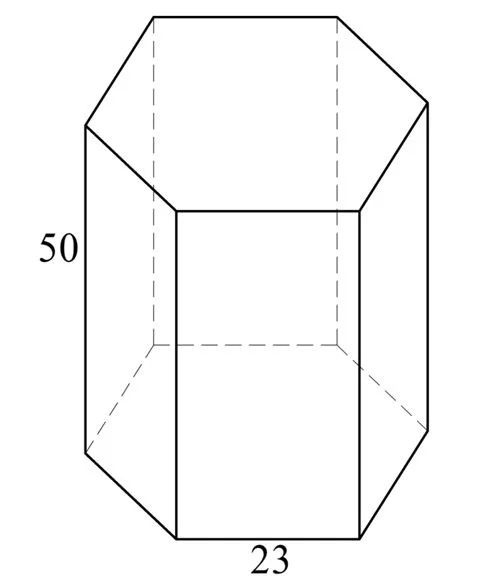
Задание. Ребро при основании правильной 6-угольной призмы имеет длину 23, а боковое ребро равно 50. Вычислите площадь поверхности призмы (и полную, и боковую).

Решение.

Сначала найдем площадь и периметр основания. Формулы для правильных многоуг-ков мы уже изучали:

Здесь а – сторона шестиугольника, R и r – радиусы описанной и вписанной окружности, n– число сторон шестиугольника. Во второй формуле мы использовали известный факт, что длина стороны правильного 6-угольника совпадает с радиусом описанной около него окружности.

Далее вычисляем площадь боковой поверхности:

Добавив к этому значению удвоенную площадь поверхности основания, найдем и полную площадь призмы:

Задание. В правильной треугольной призме АВСА₁В₁С₁, у которой все ребра одинаковы и равны единице, вычислите угол между гранью АВС и сечением АСВ₁:

Решение. Вспомним, что для нахождения угла между плос-тями необходимо построить в этих плос-тях перпендикуляры к линии их пересечения, причем эти перпендикуляры должны падать на одну и ту же точку.

Пересекаются плос-ти АВС и АСВ₁ по грани АС. Заметим, что и ∆АВС, и ∆АСВ₁ – равнобедренные, причем у них общее основание АС. Действительно, АВ = ВС, так как в основании правильной призмы лежит равносторонний треуг-к, а АВ₁ = СВ₁, так как это диагонали равных граней АВВ₁А₁ и ВСС₁В₁.

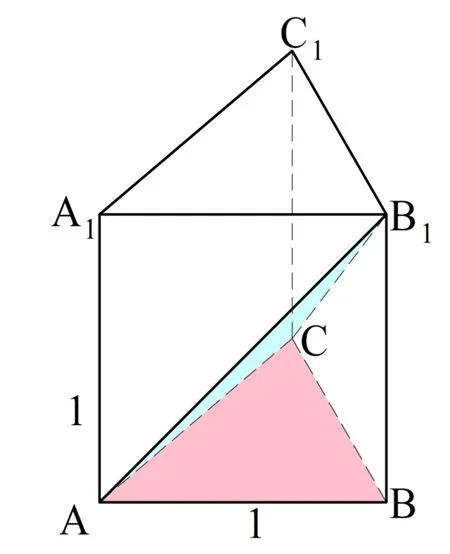
Если мы отметим середину отрезка АС (например, точкой Н) и соединим ее с В и В₁, то мы получим две медианы НВ и НВ₁, которые одновременно будут и высотой. Это значит, что именно ∠ВНВ₁ и будет искомым углом между плос-тями:

Осталось найти ∠ВНВ₁. Длину ВВ₁ мы уже знаем, она составляет 1.

АН вдвое короче АС:

Теперь заметим, что ∆НВВ₁ – прямоугольный, поэтому для него можно использовать тригонометрию:

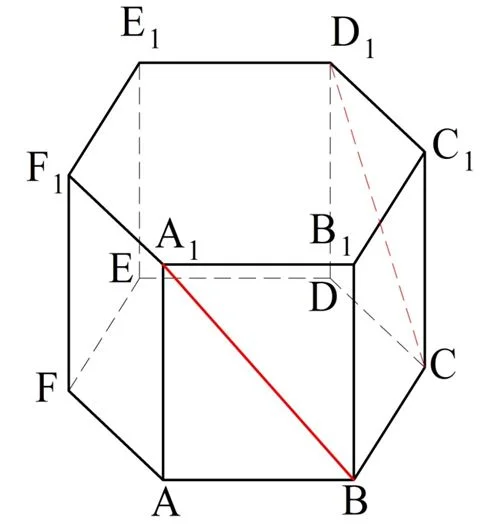
Задание. Найдите угол между прямыми А₁D и СD₁ в правильной призме, показанной на рисунке:

Все ребра этой призмы равны единице.

Решение. Сначала внимательно рассмотрим верхнее основание призмы. Так как оно представляет собой правильный многоуг-к, то вокруг него можно описать окружность. Обозначим центр этой окружности как О и проведем радиусы к вершинам:

Так как в правильном шестиуг-ке радиус описанной окружности равен стороне шестиугольника, то получается, что ∆А₁ОВ₁, ∆В₁ОС₁ и ∆С₁ОD₁ – равносторонние. Тогда ∠А₁ОВ₁, ∠B₁OC₁ и ∠С₁ОD₁ составляют по 60°. Тогда ∠А₁ОD₁ равен 180°, то есть точки А₁, О и D₁ находятся на одной прямой А₁D₁. Также заметим, что эта прямая параллельна ребру В₁С₁, ведь ∠D₁OC₁и ∠ОС₁B₁ являются накрест лежащими для этих прямых (при секущей ОС₁) и при том они одинаковы. Так как отрезки А₁О и D₁O как стороны равносторонних треуг-ков равны 1, то

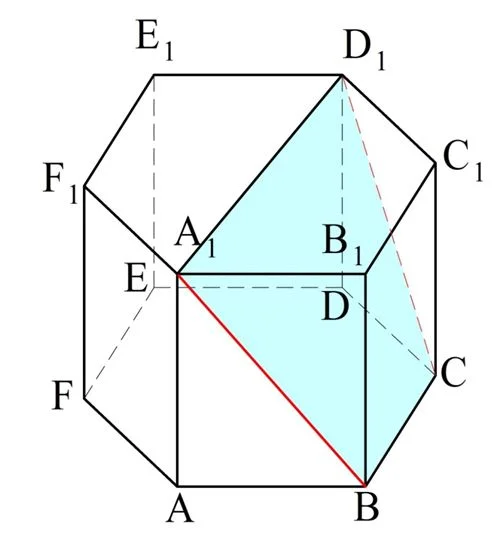
Теперь вернемся к призме:

Так как А₁D₁||В₁С₁ и В₁С₁||ВС, то и А₁D₁||ВС. Это значит, что через А₁D₁ и ВС можно провести плос-ть, в которой будут лежать и интересующие нас прямые А₁В и СD₁. Для нахождения угла между ними надо рассмотреть четырехуг-к А₁D₁CB. Раз А₁D₁||ВС, то этот четырехуг-к является трапецией.

Далее найдем длину А₁В. Для этого используем ∆АВА₁:

Аналогично из ∆СDD₁ можно определить, что СD₁ имеет такую же длину. Это значит, что А₁D₁CB – равнобедренная трапеция.

Теперь рассмотрим отдельно эту трапецию, чтобы найти искомый угол:

Опустим из вершин трапеции В и С перпендикуляры на А₁D₁. В итоге получим прямоуг-к ВСРН, где

Сегодня мы более детально изучили понятие многогранника и познакомились с новой геометрической фигурой – призмой. Призма довольно часто встречается в задаче С2 на ЕГЭ. Также мы узнали о теореме Эйлера, из которой вытекают некоторые важные факты. Один из них заключается в том, что не бывает выпуклых многогранников, у которых ни одна грань не является треуг-ком, четырехуг-ком или пятиуг-ком.

Была ли эта статья полезной?

Fsq!

Вам сюда —

http://www.genon.ru/GetAnswer.aspx?qid= … e4230f59fb

Диагональ в многоугольнике (многограннике) — отрезок, соединяющий любые две несмежные вершины, то есть, вершины, не принадлежащие одной стороне многоугольника (одному ребру многогранника).

У многогранников различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за пределы граней. У многогранников, имеющих треугольные грани есть только пространственные диагонали.

Подсчет диагоналей

Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).

Количество диагоналей N у многоугольника легко вычислить по формуле:

N = n*(n – 3)/2,

где n — число вершин многоугольника. По этой формуле нетрудно найти, что
у треугольника — 0 диагоналей
у прямоугольника — 2 диагонали
у пятиугольника — 5 диагоналей
у шестиугольника — 9 диагоналей
у восьмиугольника — 20 диагоналей
у 12-угольника — 54 диагонали
у 24-угольника — 252 диагонали

Количество диагоналей многогранника с числом вершин n легко подсчитать только для случая, когда в каждой вершине многогранника сходится одинаковое число ребер k. Тогда можно пользоваться формулой:

N = n*(n – k – 1)/2,

которая даем сумманое число пространственных и граневых диагоналей. Отсюда можно найти, что
у тетраэдра (n=4, k=3) — 0 диагоналей
у октаэдра (n=6, k=4) — 3 диагонали (все пространственные)
у куба (n=8, k=3) — 16 диагоналей (12 граневых и 4 пространственных)
у икосаэдра (n=12, k=5) — 36 диагоналей (все пространственные)
у додекаэдра (n=20, k=3) — 160 диагоналей (25 граневых и 135 пространственных)

Если в разных вершинах многогранника сходится разное число ребер, подсчет заметно усложняется и должен проводится индивидуально для каждого случая.

Фигуры с равными диагоналями

На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой. Это квадрат и правильный пятиугольник. У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом. У правильного пятиугольника пять одинаковых диагоналей, которые вместе образуют рисунок пятиконечной звезды (пентаграммы).

Единственный правильный многогранник, у которого все диагонали равны между собой — правильный восьмигранник октаэдр. У него три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра — пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).

Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой. Это куб (гексаэдр). У куба четыре одинаковых пространственных диагонали, которые также пересекаются в центре. Угол между дигоналями куба состаляет либо arccos(1/3) ≈ 70,5° (для пары диагоналей, проведенных к смежным вершинам), либо arccos(–1/3) ≈ 109,5° (для пары диагоналей, проведенных к несмежным вершинам).

Ссылки:
ru.wikipedia.org — Википедия: Диагональ
dic.academic.ru — иллюстрация разницы между граневой и пространственной диагоналями многогранника

Дополнительно в базе данных Генона:
Как найти диагональ прямоугольника?
Сколько вершин, ребер и граней у тетраэдра?
Сколько вершин, ребер и граней у куба (гексаэдра)?

Время на прочтение
8 мин

Количество просмотров 90K

Введение. Постановка вопроса.

В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично. Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.

Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:

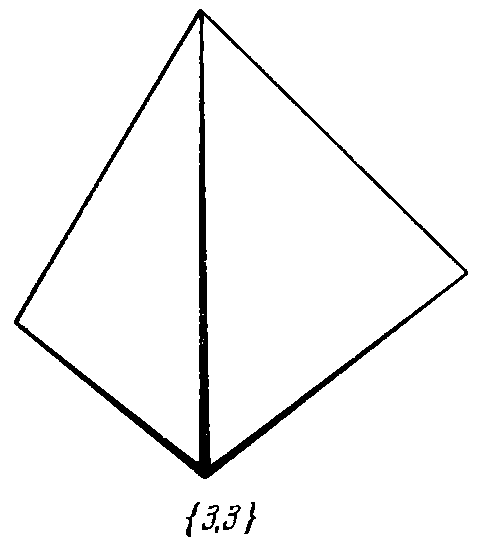
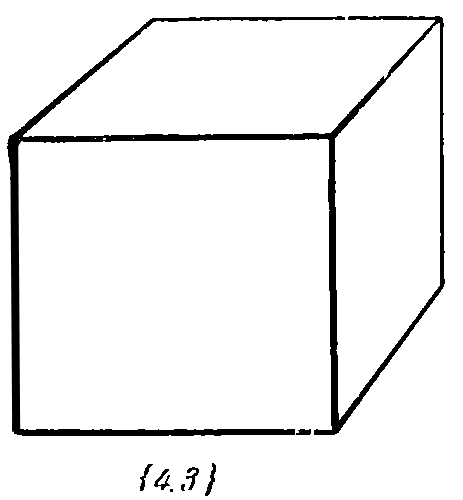
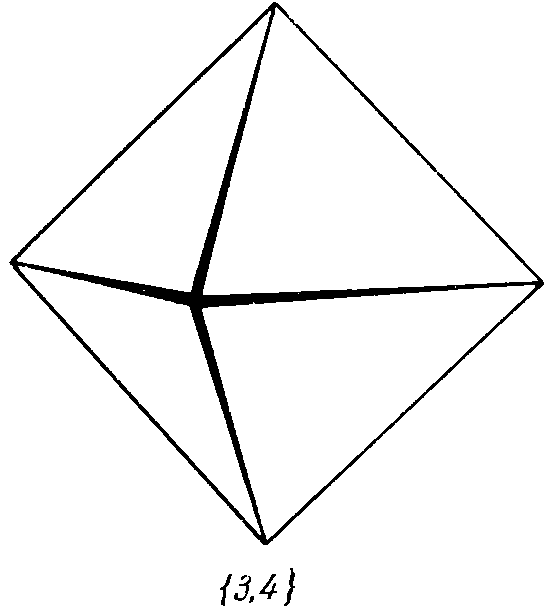
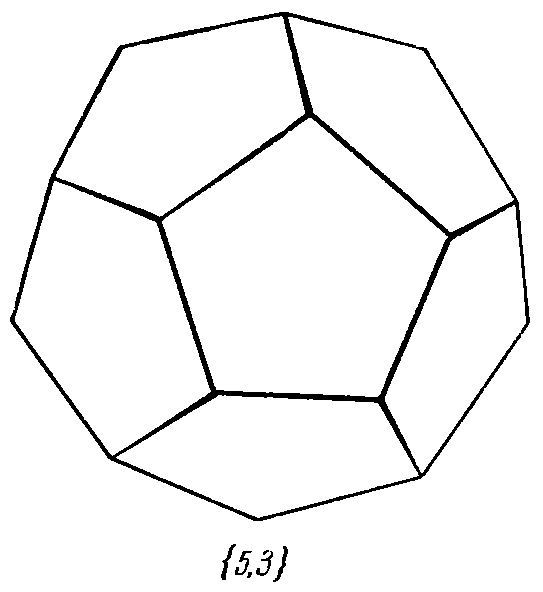
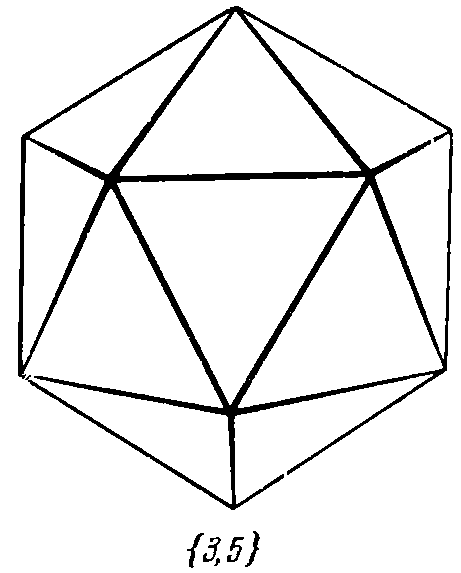
1. Тетраэдр:	2. Куб:	3. Октаэдр:	4. Додекаэдр:	5. Икосаэдр:

В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.

Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.

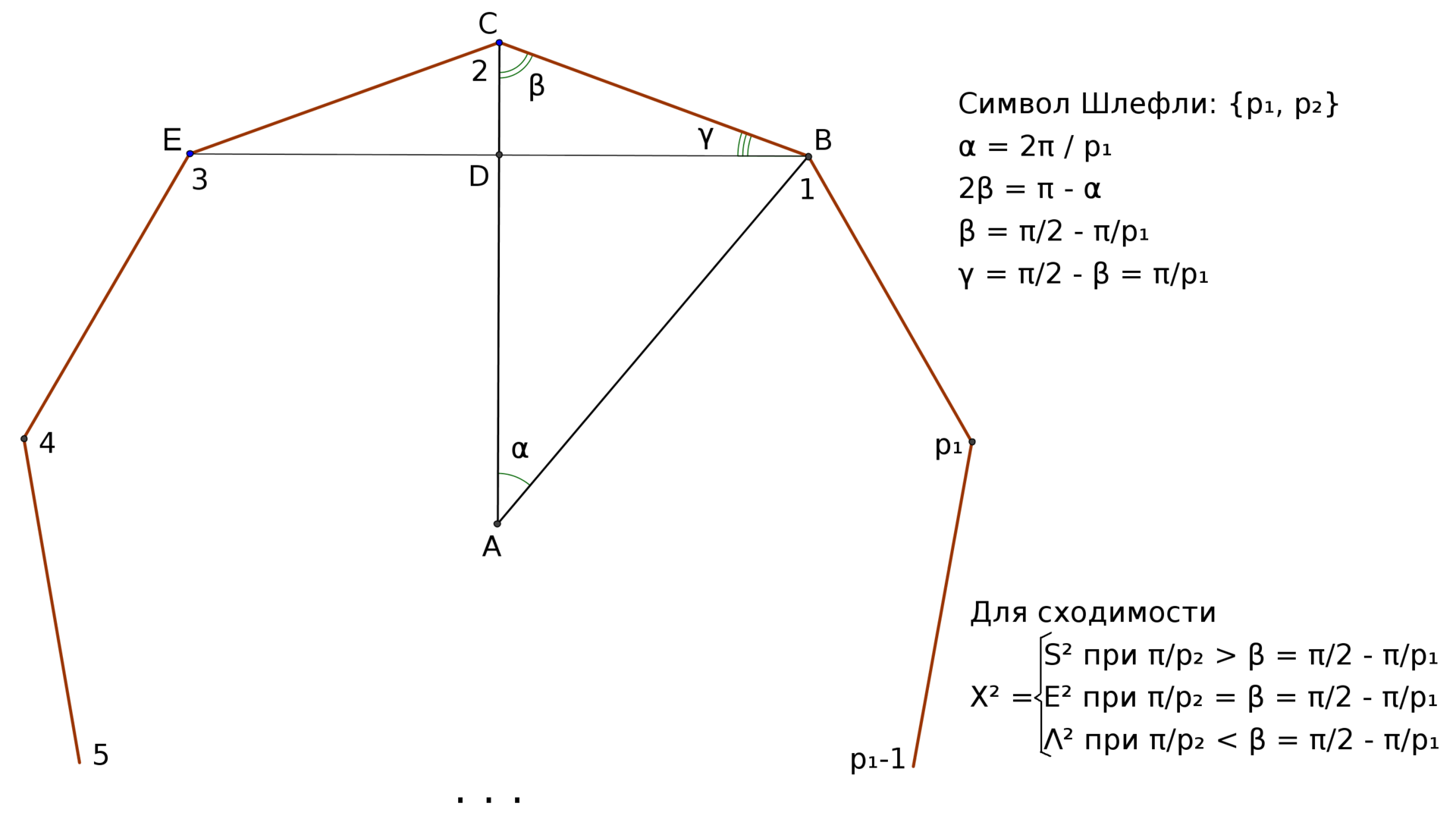
Оказывается, правильные многогранники удобно обозначать их символом Шлефли {p1, p2}, характеризующим их комбинаторное строение. Который означает, что p1 угольники, сошлись по p2 штук в вершине. Т.е. по определению p1, p2 — целые числа, большие либо равные 3. Для тех кто не знаком с понятием Символ Шлефли написал отдельную статью с картинками Символ Шлефли. Часть 2.6

В такой записи наши многогранники получат обозначения:
1. Тетраэдр {3, 3},
2. Куб {4, 3},
3. Октаэдр {3, 4},
4. Додекаэдр {5, 3},
5. Икосаэдр {3, 5}
Например, {4, 3} — куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра {3, 4} наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.

Почему правильных многогранников всего 5? Может быть их больше?

Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.

Сфера

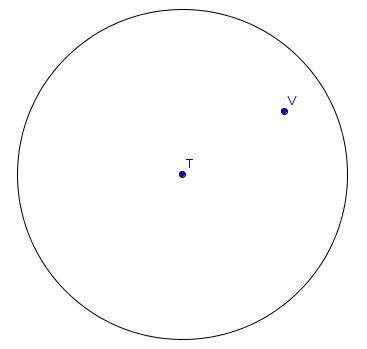
1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.

2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.

3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.

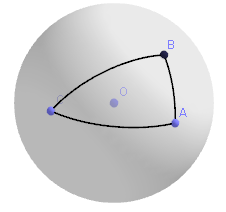
4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.

По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.

Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:

Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Лобачевский

Теперь, когда мы познакомились с геометрией на сфере, понять геометрию на гиперболической плоскости, открытую великим русским учёным Николаем Ивановичем Лобачевским, будет тоже не сложно, так как тут всё происходит аналогично сфере, только «наизнанку», «наоборот». Если дуги на сфере мы проводили окружностями, с центром внутри сферы, то теперь дуги надо проводить окружностями с центром за пределами сферы.

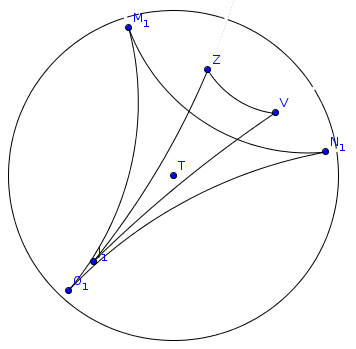
Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.

1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.

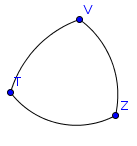
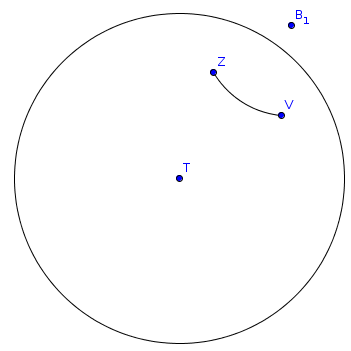
2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.

Кратчайшее расстояние строится следующим образом:

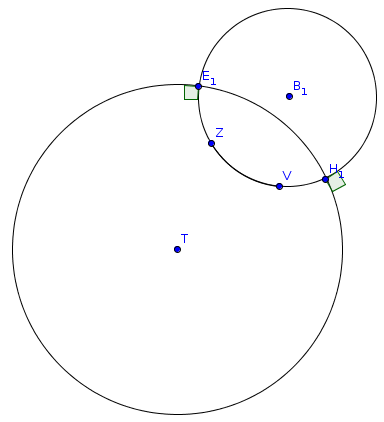
Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.

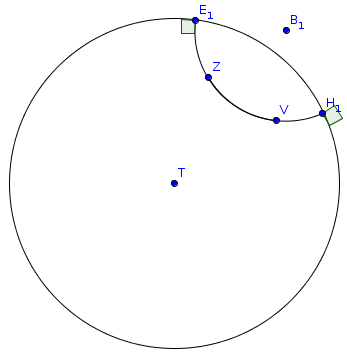
3. Убрав вспомогательные дуги, получим прямую E1 — H1 в плоскости Лобачевского.

Точки E1, H1 «лежат» на бесконечности плоскости Лобачевского, вообще край диска Пуанкаре — это всё бесконечно удалённые точки плоскости Лобачевского.

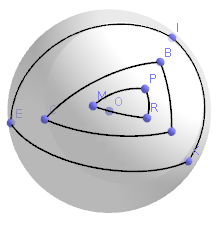
4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.

По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.

Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты сам диск Пуанкаре иногда можно не рисовать, тогда треугольник будет выглядеть немного «усохшим», «сдутым»:

Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники

Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:

Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.

Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.

Соответственно символ Шлефли икосаэдра {3, 5} — трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, {4, 4} — четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т.е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.

Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского

Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.

Итак, возьмём произвольный символ Шлефли {p1, p2}, он задаёт разбиение одного из трёх пространств постоянной кривизны (для плоскости это верно, для пространств высших размерностей дело обстоит сложнее, но ничто нам не мешает исследовать все комбинации символа).

Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.

Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:

Не трудно посчитать, что:

С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы

Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:

Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли {p1, p2}. Для решения этого уравнения надо вспомнить, так же, что p1, p2 — целые числа, большие либо равные 3. Это, так сказать, следует из их физического смысла, так как это p1 угольники (не меньше 3 углов), сходящиеся по p2 штук в вершине (тоже не меньше 3, иначе это не вершина получится).

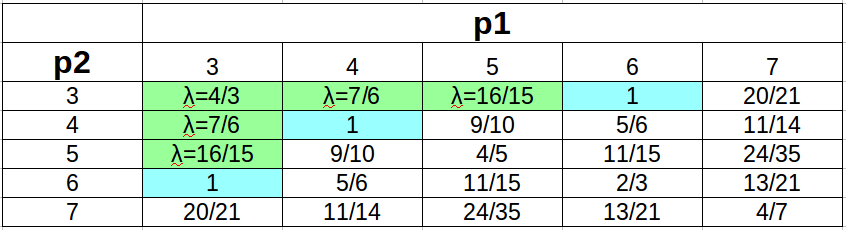
Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то {p1, p2} разбивает плоскость Евклида, если больше 1 но меньше 3, то это разбиение Сферы, если от 0 до 1, то это разбиение плоскости Лобачевского. Все эти вычисления удобно свести в таблицу.

Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: {3, 3} — тетраэдр, {3, 4} — октаэдр, {3, 5} — икосаэдр, {4, 3} — куб, {5, 3} — додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.

3. И наконец, все остальные комбинации {p1, p2} соответствуют разбиениям плоскости Лобачевского, соответственно таких разбиений бесконечное (счётное) количество. Осталось только проиллюстрировать некоторые из них, для примера.

{3, 7}

{4, 5}

{4, 6}

{4, 7}

{5, 4}

{5, 5}

{5, 6}

{5, 7}

{6, 4}

Итоги

Таким образом, правильных многогранников всего 5, они соответствуют пяти разбиениям двумерной сферы, разбиений плоскости Евклида всего 3, и разбиений плоскости Лобачевского счётное количество.
Какое приложение этих знаний?

Есть люди, которые напрямую интересуются разбиениями сферы: dxdy.ru/topic62800.html,
Есть статьи на Хабре (вот), где также рассматриваются интерпретации геометрии Лобачевского. Данная статья, возможно поможет кому-то лучше понять и познакомиться с геометрией Лобачевского.

Знание многогранников так же помогает ответить на вопрос: сколько у футбольного мяча правильных шестиугольников и сколько пятиугольников. Зная, что футбольный мяч — это усечённый икосаэдр, сразу можно дать ответ на этот вопрос: пятиугольников столько, сколько вершин у икосаэдра, шестиугольников столько, сколько граней у икосаэдра, значит, пятиугольников 12, шестиугольников 20.

Да, хотелось бы ещё рассказать про комбинаторную формулу вычисления количества вершин, рёбер и граней у этих пяти правильных многогранников, но это уже в следующий раз. И без того как-то сложновато получилось, хотя я рассчитывал на школьный уровень знаний читателей.

Так же в следующей статье при наличии интереса читателей планирую показать, как обобщается данный подход на пространства высших размерностей.

Лично для меня знание разбиений позволяет понять структуру этих пространств, особенно это актуально в размерностях выше 3.

Если вам мало трёхмерного пространства, вам понятна эта публикация и хочется забраться повыше, по размерности, то «переходите на следующий уровень»
Ссылки:
Правильные многогранники. Часть 1. Трёхмерие
Правильные многогранники. Часть 2. Четырёхмерие
Правильные многогранники. Часть 2.5 (вспомогательная)
Символ Шлефли. Часть 2.6