Как найти коллинеарные векторы в кубе - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Условия коллинеарности, ортогональности и компланарности

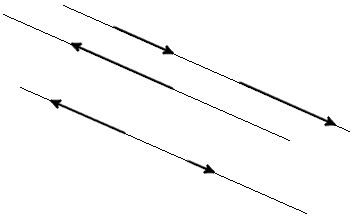
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами

Коллинеарность

Условие коллинеарности векторов 1. Два вектора $mathbf a(x_1,y_1)$ и $mathbf b(x_2,y_2)$ коллинеарны, если существует число $n$ такое, что

$$ mathbf {a} = n · mathbf {b}$$

или покоординатная детализация:

$$ x_1 = k cdot x_2 \
y_1 = k cdot y_2 \
z_1 = k cdot z_2 $$

Для коллинеарности векторов необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны

Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

$$ k = frac {x_1} {y_1} =frac {x_2} {y_2} = ldots $$

Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. [или модуль векторного произведения = 0]

$$ x_1y_2 — x_2y_1 = 0$$

Пример 1. Какие из векторов a = (1; 2), b = (4; 8), c = (5; 9) коллинеарны? Ответ — a и b.

Пример 2. Доказать что вектора a = (0; 3) и b = (0; 6) коллинеарны.

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n. $na = (2 · 0; 2 · 3) = (0; 6)$

Пример 3. Образуют ли базис векторы k(3,7), -6,14)?

Ответ: да. Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы).

В общем случае нужно составить систему уравнений (по условию 1) и исследовать ее на совместность. Если несовместна (решений нет) — значит, вектора ЛН. В данном случаи можно действовать упрощенно по условию 2, так как нет нулей и деления на них.

Пример 4. Даны вершины четырёхугольника A(-4,2), B(2,6), C(5,4), D(-1,0). Доказать, что четырёхугольник ABCD является параллелограммом.

Доказательство: Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Нужно доказать:

параллельность противоположных сторон AB и CD;
параллельность противоположных сторон BC и AD.

Найти вектора и проверить на коллинеарность.

Систематизируем: Для двух векторов плоскости эквивалентны следующие утверждения:

векторы линейно независимы;
векторы образуют базис;
векторы не коллинеарны;
векторы нельзя линейно выразить друг через друга;
определитель, составленный из координат данных векторов, отличен от нуля.

Ортогональность

Вектора a и b называются ортогональными, если угол между ними равен 90°.

Условие ортогональности векторов. Два вектора a и b ортогональны, если их скалярное произведение равно нулю.

$$ x_1x_2 + y_1y_2 = 0$$

или в трехмерном случае:

$$ x_1x_2 + y_1y_2 + z_1z_2 = 0$$

Пример 1. Доказать что вектора a = (1; 2) и b = (2; -1) ортогональны.

Пример 2. Найти значение числа n при котором вектора a = (2; 4) и b = (n; 1) будут ортогональны.

Ответ -2

Пример 4. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.
Ответ : да

Компланарность

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Всегда возможно найти плоскости параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.

Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга.

Условия компланарности векторов

Три вектора компланарны если их смешанное произведение равно нулю.

Три вектора компланарны если они линейно зависимы.

Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

Пример 1. Проверить компланарны ли три вектора a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.

Решение: найдем смешанное произведение векторов

a · [b × с] =
1  	  2  	  3  	 =
1  	  1  	  1  
1  	  2  	  1  
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Признаки параллельности и перпендикулярности прямых

Пусть даны две прямые a и b, заданные уравнениями:
$$ a: y = k_1 x + c_1 \
b: y = k_2 x + c_2
$$

Возьмем два произвольных вектора, по одному на каждой прямой. Например, при x=0 и x=1 прямая a проходит через точки $(0, c_1)$ и $(1, k_1 + c_1)$. Значит, вектор, лежащий на прямой a можно задать координатами $(1, k_1)$

Аналогично, вектор, лежащий на прямой b можно задать координатами $(1, k_2)$

Векторы коллинеарны, если $k_1 = k_2$ — совпадают угловые коэффициенты прямых, значит, прямые параллельны

Векторы ортогональны, если скалярное произведение $k_1 cdot k_2 + 1 = 0$ или $k_1 k_2 = -1$, прямые перпендикулярны

Источник

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

a = n · b

Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = {a_x; a_y; a_z} и b = {na_x; na_y; na_z}. Найдем их векторное произведение

a × b =

ijk
a_xa_ya_z
b_xb_yb_z

= i (a_yb_z — a_zb_y) — j (a_xb_z — a_zb_x) + k (a_xb_y — a_yb_x) =

= i (a_yna_z — a_zna_y) — j (a_xna_z — a_zna_x) + k (a_xna_y — a_yna_x) = 0i + 0j + 0k = 0

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

Значит:

Вектора a и b коллинеарны т.к.	1	=	2	.
4	8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
5	9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
4	8

Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

b = na.

Для этого найдем ненулевой компонент вектора a в данном случае это a_y. Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение na:

na = {2 · 0; 2 · 3} = {0; 6}

Так как b = na, то вектора a и b коллинеарны.

Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

Значит:

Решим это уравнение:

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

Значит:

Вектора a и b коллинеарны т.к.
14 = 28 = 312

Вектора a и с не коллинеарны т.к.
15 = 210 ≠ 312

Вектора с и b не коллинеарны т.к.
54 = 108 ≠ 1212

Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.

b = na.

Для этого найдем ненулевой компонент вектора a в данном случае это a_y. Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение na:

na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}

Так как b = na, то вектора a и b коллинеарны.

Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

Значит:

3	=	2	=	m
9	n	12

Из этого соотношения получим два уравнения:

Решим эти уравнения:

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Источник

Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом или . Вектор называется противоположным
вектору и может быть
обозначен .

Сформулируем ряд базовых определений.

Длиной
или модулем
вектора  называется
длина отрезка и обозначается . Вектор нулевой длины (его суть — точка) называется нулевым  и направления
не имеет. Вектор единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора  .

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.

Векторы
называются равными , если они коллинеарны, одинаково направлены и имеют
одинаковые длины.

Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.

Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через соответственно.
Выберем произвольный вектор

пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через a_x, a_y, a_z
соответственно. Тогда нетрудно показать, что

. (2.25)

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора

:

, (2.26)

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.

Пусть в трехмерном пространстве заданы векторы своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.

Геометрически
два вектора складываются по двум правилам:

а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;

б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.

2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если , то

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: . Координаты векторов и совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно:.

При λ>0
– вектор сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана
направленная прямая (ось l), вектор задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.

Проекцией вектора на ось l называется длина вектора , взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.

Если
в качестве оси l взять некоторый другой вектор , то получим проекцию вектора на вектор .

Рассмотрим некоторые
основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть ;

2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;

3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.

5. Скалярным произведением векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

. (2.27)

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол , поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Теорема 2.3. Скалярное произведение двух векторов ,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

(2.28)

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:

(2.29)

Отсюда
следует условие перпендикулярности ненулевых векторов
и :

(2.30)

Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле

(2.31)

С помощью скалярного произведения векторов находят
работу постоянной силы на
прямолинейном участке пути.

Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения (рис. 2.14). Физика утверждает, что работа силы при перемещении
равна .

Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.

Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах

Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):

Отсюда согласно формуле (2.29) получим косинус
искомого угла

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?

Таблица 2.2

Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции и вектор цены единицы
соответствующего ресурса .

Тогда . Общая цена
ресурсов , что представляет собой скалярное произведение
векторов . Вычислим его по формуле (2.28) согласно теореме 2.3:

Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix

Пример 2.11. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?

Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала

. По формуле (2.28) (единиц работы).

Угол φ между и
находим по
формуле (2.29), то есть

6. Три некомпланарных вектора , взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.

Векторным
произведением вектора на вектор называется
вектор , удовлетворяющий следующим условиям:

– перпендикулярен векторам и ;

– имеет длину, равную , где φ – угол, образованный векторами
и ;

– векторы образуют правую
тройку (рис. 2.15).

Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения

Теорема 2.5. Векторное произведение векторов , заданных своими координатами, равно определителю
третьего порядка вида

(2.32)

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен . С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна

. Следовательно,

. (2.33)

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.

Пусть в точке A приложена
сила  и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы  относительно
точки O называется вектор , который проходит через точку O и удовлетворяет следующим условиям:

— перпендикулярен плоскости, проходящей через точки O, A, B;

— его модуль численно равен произведению силы на плечо .

— образует правую тройку с векторами и .

Следовательно,
момент силы относительно
точки O представляет собой векторное произведение

. (2.34)

Линейная скорость точки М твердого тела, вращающегося с
угловой скоростью вокруг
неподвижной оси, определяется формулой Эйлера , O – некоторая неподвижная

точка оси (рис. 2.17).

Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть . Тогда площадь треугольника
. Следовательно, искомая площадь равна (единиц
площади)

7. Рассмотрим произведение трех векторов , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение называется смешанным
произведением трех векторов
(векторно–скалярным произведением).

Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

(2.35)

Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов .

Объем треугольной пирамиды, построенной на этих же
векторах, равен

(2.36)

Пример 2.13. Вершинами пирамиды служат точки . Вычислить объем пирамиды.

Решение. Найдем
координаты векторов

. Вычислим смешанное произведение этих векторов:

По формуле (2.36) объем пирамиды, построенной на
векторах равен
(единиц объема)

Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.

Система векторов называется
линейно зависимой, если существуют такие числа , хотя бы одно из которых отлично от нуля, что имеет
место равенство

(2.37)

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что . Тогда на это число разделим равенство (2.37), имеем:

получим выражение вектора через
остальные векторы

Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все

В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).

Базисом n – мерного
пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса

таким образом:

Числа
называются координатами
вектора в базисе
векторов .

Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.

Например, в трехмерном пространстве
существует базис единичных орт  такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор  трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ): Коэффициенты {x₁, x₂, x₃} такого разложения вектора
по ортам  являются координатами вектора  в трехмерном
пространстве.

Вопросы для самопроверки

Источник

Коллинеарность векторов, условия коллинеарности векторов.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).

рис. 1

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = < a_x ; a_y ; a_z > и b = < na_x ; na_y ; na_z >. Найдем их векторное произведение

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Вектора a и b коллинеарны т.к.	1	=	2	.
4	8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
5	9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
4	8

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решим это уравнение:

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12

Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12

Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
a_y	3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

a_x	=	a_y	=	a_z	.
b_x	b_y	b_z

3	=	2	=	m
9	n	12

Из этого соотношения получим два уравнения:

Решим эти уравнения:

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Коллинеарные векторы

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Условия коллинеарности векторов

Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

1. Существует такое число n, при котором .

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Примеры задач

Задание 1
Даны векторы , и . Определим, есть ли среди них коллинеарные.

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Следовательно, коллинеарными являются только векторы a и c .

Задание 2
Выясним, при каком значении n векторы и коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Условие коллинеарности векторов

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.

Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R

Координатная форма условия коллинеарности векторов

Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .

По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1

Т.е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7

тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .

Ответ: при p = 6 7 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .

Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .

Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.

Решение

Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )

источники:

Коллинеарные векторы

http://zaochnik.com/spravochnik/matematika/vektory/uslovie-kollinearnosti-vektorov/

Источник

Любовь Петровна Гаврилюк

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Понятие коллинеарности векторов

Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Определение 1

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Определение 2

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ

Определение 3

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Обозначение: $overline{0}$.

Далее рассмотрим, какие векторы называются коллинеарными.

Определение 4

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).

«Как найти вектор, коллинеарный вектору» 👇

Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ

Также введем определение векторного произведения, которое будет нам необходимо далее.

Определение 5

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам

Теорема 1

Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.

Доказательство.

Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Так как векторы $overline{α}$ и $overline{β}$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $overline{α}↑↑overline{β}$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $roverline{α}$ и $overline{β}$ были равны между собой. По определению умножения векторов на число, получим, что $roverline{α}↑↑overline{β}$. Но тогда, по определению равенства векторов, получим, что $roverline{α}=overline{β}$. Из этого равенства получим, что

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут коллинеарными.

Из данных равенств следует, что $roverline{α}=overline{β}$.

Имеются два случая:

$r lt 0$

В этом случае, по определению умножения вектора на число, получим, что $roverline{α}↑↓overline{β}$.
$r >0$

В этом случае получим, что $roverline{α}↑↑overline{β}$.

Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline{α}$ и $overline{β}$.

Ответ: теорема доказана.

Пример 1

Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.

Доказательство.

Разложим второй вектор:

$(9,-3)=(3cdot 3,3cdot (-1) )=3(3,-1)$

Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.

Признаки и свойства коллинеарности векторов через их произведение

Теорема 2

Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.

Доказательство.

Так как векторы коллинеарны, то, по теореме 1, верны равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Найдем $overline{α}хoverline{β}$ по формуле

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rβ_1&rβ_2&rβ_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\β_1&β_2&β_3\β_1&β_2&β_3end{vmatrix}=rcdot overline{0}=overline{0}$

Достаточность: Пусть верно равенство $overline{α}хoverline{β}=overline{0}$, докажем, что векторы $overline{α}$ и $overline{β}$ коллинеарны. Так как векторное произведение равняется $overline{0}$, то его длина также равняется нулю. Следовательно, угол между $overline{α}$ и $overline{β}$ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.

Теорема доказана.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник