Как найти компланарные векторы в параллелепипеде - Исправление недочетов и поиск решений вместе с Examum.ru

Одно из определений компланарных векторов гласит:

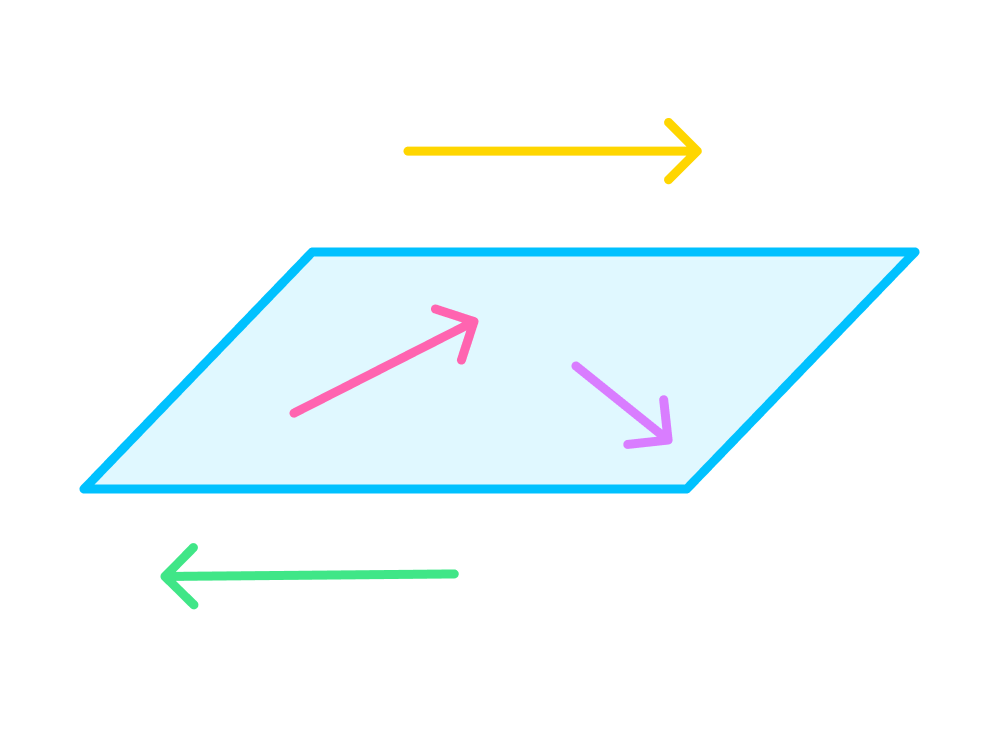
векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.

Тот же смысл имеет и другое определение:

три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Обрати внимание!

Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.

Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.

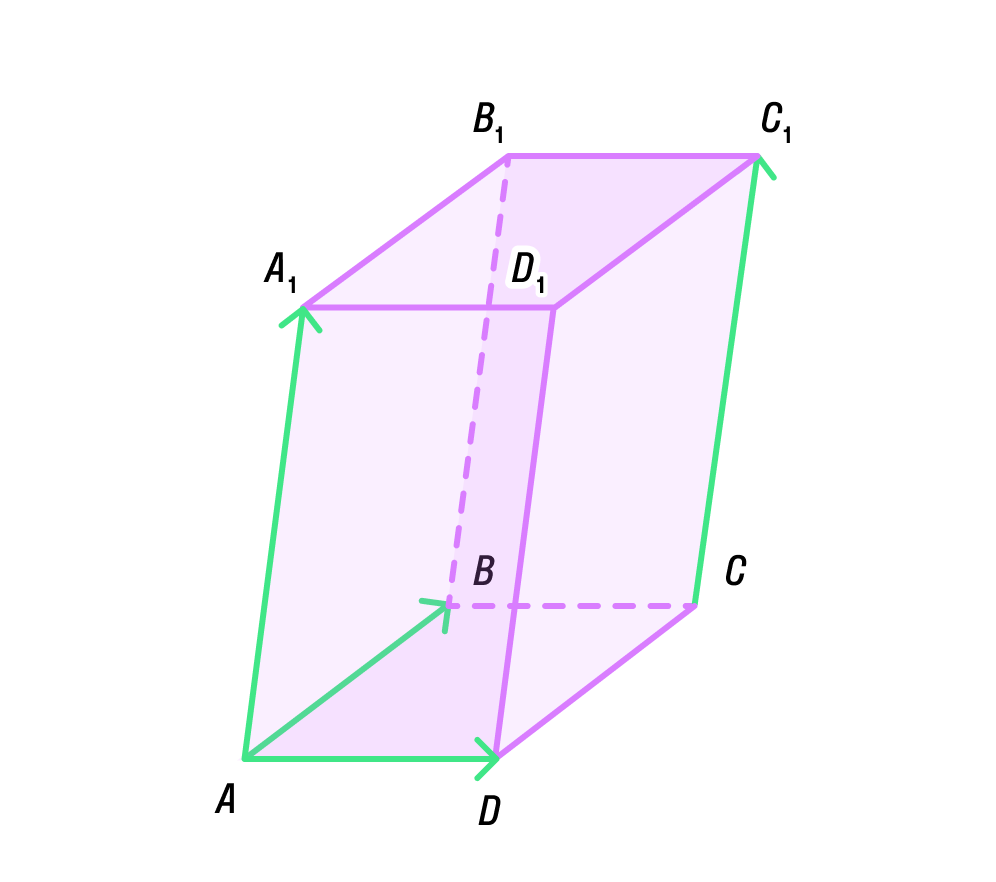
Все вышеупомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда.

1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы

AA1→

CC1→

AD→

, то есть, эти векторы компланарны. Также компланарны векторы

AA1→

AB→

CC1→

, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор

CC1→

совпадёт с вектором

AA1→

2. Например, векторы

AB→

AD→

AA1→

не компланарны, так как их нельзя разместить в одной и той же плоскости.

Признак компланарности трёх векторов:

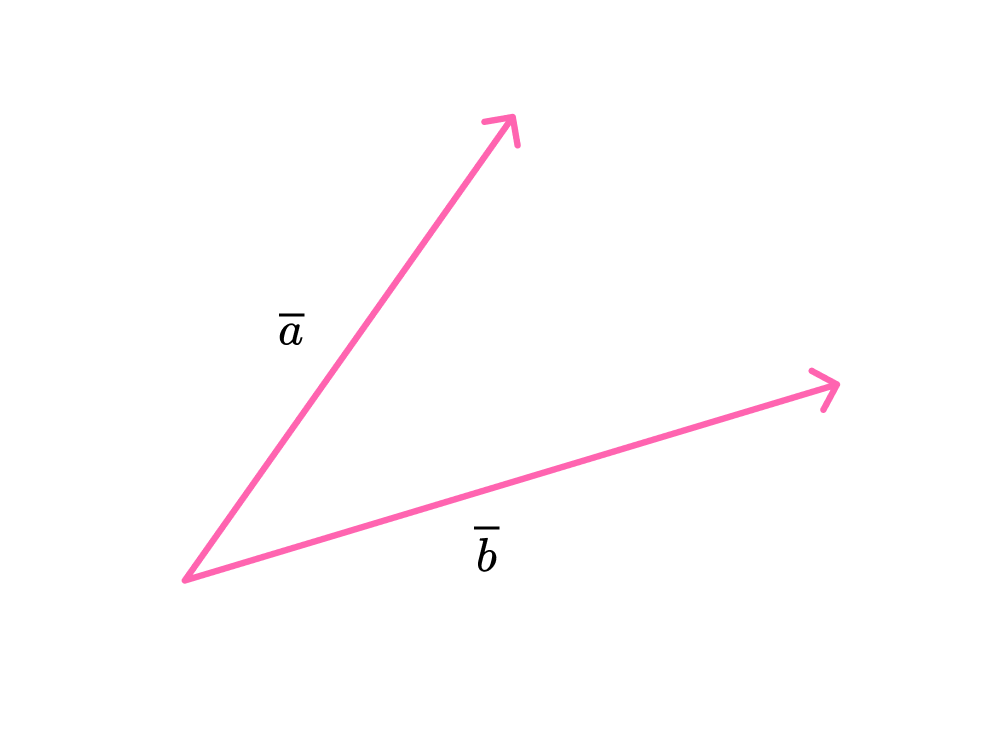
пусть векторы

a→

b→

не коллинеарны. Если для вектора

c→

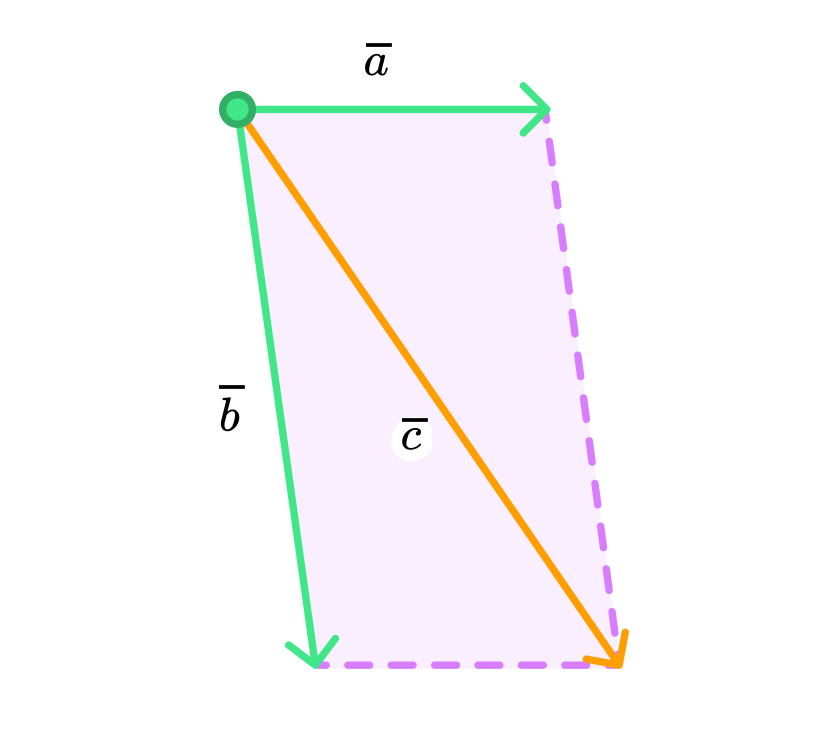
существует единственная пара реальных чисел (x) и (y), такая, что

c→=x⋅a→+y⋅b→

, то векторы

a→

b→

c→

компланарны.

Справедливо и обратное утверждение:

если три вектора

a→

b→

c→

компланарны и векторы

a→

b→

не коллинеарны, то вектор

c→

можно разложить по векторам

a→

b→

одним-единственным образом.

Если разложить вектор

AC→

по векторам

AA1→

AA2→

, то это можно сделать одним-единственным образом:

AC→=AB→+AD→=x⋅AA1→+y⋅AA2→

Если три вектора некомпланарны, то для их сложения в пространстве применяется закон параллелепипеда.

1. Векторы приводят к общему началу (A).

2. На этих трёх рёбрах строится параллелепипед.

3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов

AB→

AD→

AA1→

Разложение вектора по трём некомпланарным векторам

Теорема о разложении по базису в пространстве
Любой вектор

d→

можно разложить по трём данным некомпланарным векторам

a→

b→

c→

, причём реальные коэффициенты разложения (x), (y) и (z) определяются единственным образом:

AC1→=AD→+AB→+AA1→=x⋅AA2→+y⋅AA3→+z⋅AA4→

Источник

Понятие компланарности векторов

Как мы уже сказали, компланарность векторов связана с их расположением в пространстве. Чтобы понять, какие векторы называют компланарными, давайте рассмотрим несколько определений, которые раскрывают это понятие с разных сторон.

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Компланарные векторы — это векторы, которые лежат в одной плоскости или параллельны одной плоскости.

Как вы думаете, всегда ли можно найти плоскость, параллельную двум векторам? Да, вы абсолютно правы! Именно поэтому любые два произвольных вектора можно считать компланарными.

Но если векторов не два, а три, то, чтобы назвать их компланарными, нужно выполнить определенные условия.

Давайте рассмотрим эти условия компланарности на примере векторов а, b и с. Эти векторы компланарны, когда:

Пары векторов а и с, b и c, a и b компланарны между собой.
Любая пара этих векторов коллинеарна (т. е. лежит на одной прямой или двух параллельных прямых).
Все три вектора лежат в одной плоскости.

Давайте найдем пример компланарных и некомпланарных векторов, которые разместим на ребрах параллелепипеда:

векторы АА₁, СС₁ и СВ компланарны, так как АА₁ и СС₁ коллинеарны;
векторы АВ, DC и DD₁ компланарны, так как АB и DC коллинеарны;
векторы CD, CB и CC₁ некомпланарны, так как они не лежат в одной плоскости и любая пара векторов не является коллинеарной.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Теоремы, связанные с компланарностью трех векторов

Теорема 1

Первая теорема не связана непосредственно с вопросом компланарности, но нам все равно необходимо ее вспомнить, так как она является вспомогательной.

Звучит она так: любой произвольный вектор можно разложить по двум неколлинеарным векторам только с единственными коэффициентами разложения:

Теорема 2

Если один из трех векторов можно разложить по двум другим векторам с единственными коэффициентами разложения, то эти векторы являются компланарными.

Давайте попробуем доказать эту теорему. Для этого возьмем три вектора: с, b и е, где

Пусть векторы b и е являются коллинеарными. Тогда векторы с, b и е точно являются компланарными по свойству: если два из трех векторов коллинеарны, то все три можно считать компланарными.
Допустим, векторы b и е не являются коллинеарными. Тогда мы разложили вектор с по двум неколлинеарным векторам, что соответствует теореме 1. А это, в свою очередь, говорит о том, что векторы с, b и е лежат в одной плоскости и являются компланарными.

Теорема доказана!

Теорема 3

Если три вектора а, b и с являются компланарными, а векторы а и b — неколлинеарными, то вектор с можно разложить через а и b единственным образом:

Эта теорема очень похожа на предыдущую, правда? Давайте обратим внимание на то, каким образом можно доказать то, что она верна.

Раз векторы а, b и с компланарны, значит, существует такая плоскость, параллельная исходной, в которой можно построить векторы а₁ = а, b₁ = b, с₁ = с. Раз а и b неколлинеарны, значит, новые векторы а₁ и b₁ тоже будут неколлинеарными. А значит, согласно теореме 1, мы можем разложить вектор с₁ = ха₁ + уb₁.

Следовательно,

Признак и критерий компланарности векторов

С теоремами мы успешно разобрались — пришло время перейти к завершающей части. Для полной картины нам необходимо поговорить еще о некоторых нюансах, касающихся компланарных векторов.

Линейно зависимыми называются векторы

, из которых можно составить линейную комбинацию, равную нулю:

Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a и векторного произведения b · c, т. е. число a (b · c), или (b · c) a.

Признаки компланарности векторов:

Если смешанное произведение трех векторов равно нулю, то эти три вектора компланарны.
Если три вектора линейно зависимы, то они компланарны.

Эти признаки редко подробно изучают в школьном курсе. Но ведь приятно знать то, о чем даже не догадываются твои одноклассники? 😉

Практика

Мы много узнали, теперь осталось закрепить теорию практическим заданием.

Дан параллелепипед АВСDА₁В₁С₁D₁. Разложите вектор D₁B₁ по DC и CB.

Решение.

Плоскости (АВС) и (А₁В₁С₁) параллельны, так как находятся на противоположных гранях параллелепипеда. Значит, векторы D₁B₁, DC и CB являются компланарными. Поэтому по теореме 2 мы сможем провести разложение D₁B₁ по DC и CB, причем единственным способом:

DB = D₁B₁, DC = D₁C₁, CB = C₁B₁.

Согласно правилу треугольника, DB = DC + CB.

А так как DB = D₁B₁, значит, и D₁B₁ = DC + CB.

В геометрии достаточно много тем, которые требуют детального изучения: в них есть теоремы, аксиомы, интересные логические умозаключения. Разобраться во всем этом вам помогут курсы профильной математики в онлайн-школе Skysmart. На них ребенок не только станет настоящим экспертом в точных науках, но и проведет время увлекательно и даже весело. Приходите вместе на бесплатный вводный урок и убедитесь сами!

Источник

Скачать материал

Компланарные
векторы.
Правило параллелепипеда

Скачать материал

Сейчас обучается 139 человек из 43 регионов

Сейчас обучается 49 человек из 26 регионов

Описание презентации по отдельным слайдам:

1 слайд

Компланарные
векторы.
Правило параллелепипеда
2 слайд

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
c
Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
a
c
Любые два вектора компланарны.
2
3 слайд

Три вектора, среди которых имеются два коллинеарных, также компланарны.
c
a
k
3
4 слайд

Три произвольных вектора могут быть как компланарными, так и не компланарными.
На рисунке изображен параллелепипед.
А
О
Е
D
C
Являются ли векторы ВВ1,

ОD и ОЕ компланарными?
В
B1
4
5 слайд

Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед.
А
О
Е
D
C
В
B1
Векторы ОА, ОВ и ОС не компланарны, так как вектор

ОС не лежит в плоскости ОАВ.
Являются ли векторы ОА,

ОВ и ОС компланарными?
5
6 слайд

B
C
A1
B1
C1
D1
Являются ли векторы AD, А1С1 и D1B компланарными?
Векторы А1D1, A1C1 лежат в плоскости А1D1C1.

Вектор D1В не лежит в этой плоскости.
Векторы AD, А1С1 и D1B не компланарны.
A
D
6
7 слайд

A
B
C
A1
B1
C1
D1
D
Являются ли векторы AD и D1B компланарными?
Любые два вектора компланарны.
7
8 слайд

№355 Дан параллелепипед АВСA1B1C1D1.
Компланарны ли векторы?
В
А
В1
С1
D1
D
С
А1
АА1, СС1, ВВ1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
8
9 слайд

№355 Дан параллелепипед АВСA1B1C1D1.
Компланарны ли векторы?
В
А
В1
С1
D1
D
С
А1
АВ, АD, АА1
Векторы АВ, АD и АА1 не компланарны, так

как вектор АА1 не лежит в плоскости АВС.
9
10 слайд

№355 Дан параллелепипед АВСA1B1C1D1.
Компланарны ли векторы?
В
А
В1
С1
D1
D
С
А1
В1В, АС, DD1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
10
11 слайд

№355 Дан параллелепипед АВСA1B1C1D1.
Компланарны ли векторы?
В
А
В1
С1
D1
D
С
А1
АD, CC1, А1B1
Векторы АВ, АD и АА1 не компланарны, так

как вектор АА1 не лежит в плоскости АВС.
АD, CC1, А1B1
Векторы
не компланарны
12 слайд

Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Если вектор можно разложить по векторам

и , т.е. представить в виде

где x и y – некоторые числа, то векторы , и

компланарны.
c
a
b
c = xa + yb
a
b
c
Признак компланарности
12
13 слайд

c = xa + yb
Докажем, что векторы компланарны.
b
О
В
В1
А1
А
С
ОВ1 = у ОВ
ОА1 = х ОА
Векторы ОА и ОВ лежат в одной плоскости ОАВ.
Векторы ОА1 и ОВ1 также лежат плоскости ОАВ.
А следовательно, и их сумма – вектор ОС = х ОА + у ОВ,

равный вектору .
c
c
a
13
14 слайд

Если вектор можно разложить по векторам

и , т.е. представить в виде

где x и y – некоторые числа, то векторы , и

компланарны.
c
a
b
c = xa + yb
a
b
c
Признак компланарности
Справедливо и обратное утверждение.
Если векторы , и компланарны, а векторы

и не коллинеарны, то вектор можно

разложить по векторам и

, причем

коэффициенты разложения определяются

единственным образом.
c
a
b
c = xa + yb
a
b
c
a
b
14
15 слайд

Сложение векторов.
Правило треугольника.
a
a
b
b
a +
b
АВ + ВС =
АС
П
О
В
Т
О
Р
И
М

15
16 слайд

Сложение векторов. Правило параллелограмма.
a
a
b
b
a +
b
b
a +
АВ + АD =
АС
А
В
D
C
П
О
В
Т
О
Р
И
М

16
17 слайд

Сложение векторов.
Правило многоугольника.
= АO
АВ + ВС + СD + DO
a
c
n
m
c
m
n
a+c+m+n
a
П
О
В
Т
О
Р
И
М

17
18 слайд

A
В
С
В1
D
Е
Правило параллелепипеда.
a
b
c
О
OE + ED
= (OA + AE) + ED
= OA + OB + OC =
= a + b + c
OA + OB + OC = OD
из OED
из OAE
OD =
19 слайд

Теорема о разложении вектора по трем некомпланарным векорам.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Разложение вектора по трем некомпланарным векторам. Если вектор представлен в виде

где , и — некоторые числа, то говорят, что вектор

разложен по векторам , и . Числа , и

называются коэффициентами разложения.
p = xa + yb + zc
c
x
z
p
y
b
a
x
z
y
19
20 слайд

p = xa + yb + zc
Докажем, что любой вектор можно представить в виде
p
b
c
a
p
C
B
P1
A
P
P2
a
b
c
p
O
По правилу многоугольника
ОР = ОР2 + Р2Р1 + Р1Р
ОР2 = x OA
Р2Р1= у OВ
Р1Р = z OC
ОР = x OA + y OB + z OC
p = xa + yb + zc
20
21 слайд

Если предположить, например, что , то из этого

равенства можно найти

Докажем теперь, что коэффициенты разложения определяются единственным образом. Допустим, что это не так и существует другое разложение вектора
p = x1a + y1b + z1c
p = xa + yb + zc
–
o = (x – x1)a + (y – y1)b + (z – z1)c
Это равенство выполняется только тогда,
когда
o
o
o
Тогда векторы компланарны. Это противоречит условию теоремы. Значит, наше предположение не верно,
и
Следовательно, коэффициенты

разложения определяются
единственным образом.
21
22 слайд

D
В
A
С
B1
C1
D1
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
АВ + АD + АА1
A1
= AC1
22
23 слайд

В
A
С
C1
D1
D
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
DА + DC + DD1
A1
= DB1
B1
23
24 слайд

В
A
С
C1
D1
D
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
A1
= DB1
B1
A1B1 + C1B1 + BB1
DC
+ DD1
+ DA
24
25 слайд

В
A
С
C1
D1
D
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
A1
= A1C
B1
A1A + A1D1 + AB
+ A1B1
A1A + A1D1
25
26 слайд

В
A
С
C1
D1
D
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
A1
= BD1
B1
B1A1 + BB1 + BC
BA +
BB1 + BC
26
27 слайд

В
A
С
C1
D1
D
№359 Дан параллелепипед АВСA1B1C1D1.

Разложите вектор BD1 по векторам BA, ВС и ВВ1.
A1
B1
ВD1 = BA + BC + BB1
По правилу параллелепипеда
27
28 слайд

В
A
С
C1
D1
D
№359 Дан параллелепипед АВСA1B1C1D1.

Разложите вектор B1D1 по векторам А1A, А1В и А1D1.
A1
B1
В1D1 = B1A1+ А1D1
По правилу треугольника из А1В1D1:
из А1В1B
= (В1B + BA1)+ А1D1
=
= (A1A – A1B)+ А1D1
=
=
= A1A – A1B+ А1D1
29 слайд

Правило параллелепипеда

a Пусть даны некоторые некомпланарные векторы
c a , b, c
b
30 слайд

Правило параллелепипеда

С Отложим от некоторой
точки О пространства векторы ОА=a , ОВ=b, ОС=c и построим паралле-
c лепипед так, чтобы В отрезки ОА,ОВ,ОС были его рёбрами.
О А
b
a
31 слайд

Правило параллелепипеда
D
С Диагональ OD этого
параллелепипеда изобра- жает сумму векторов
a , b , и c
c
О А

b
a
32 слайд

Правило параллелепипеда
D
С OD=a + b +c .
Действительно,
OD=OE + ED=(OA +AE)+ + ED= OA+ 0B + OC =
= a +b +c
В Е
О А
33 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
а) АВ+ВD+DC
34 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
а) АВ+ВD+DC
A

D
B

C
35 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
а) АВ+ВD+DC
A Решение.
AB+BD= AD, AD+DC=AC

D Ответ: АС
B

C
36 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
б) АD+CВ+DC
37 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
б) АD+CВ+DC
A

D
B

C
38 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
б) АD+CВ+DC
A Решение.
AD+DC= AC, AC+CB=AB

D Ответ: АB
B

C
39 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
в) АB+CD+BC+DA
40 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
в) АB+CD+BC+DA
A

D
B

C
41 слайд

Решение задач
№ 379 Дан тетраэдр АВСD. Найдите сумму векторов:
в) АB+CD+BC+DA
A Решение.
AB+BC= AC, AC+CD=AD, AD+DA=0

D Ответ: 0
B

C
42 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
а) AB+AD+A А1
43 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
а) AB+AD+A А1
B1 С1
А1 D1

B С
А D
44 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
а) AB+AD+A А1
B1 С1
А1 D1 Решение

AB+AD = АС
АС + A А1 = АС1

B С Ответ : АС1
А D
45 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
б) DA+DC+D D1
46 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
б) DA+DC+D D1
B1 С1
А1 D1

B С
А D
47 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
б) DA+DC+D D1
B1 С1
А1 D1 Решение

DA+DC = DB
DB + DD1 = DB1

B С Ответ : DB1
А D
48 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
в) А1B1+С1B1 +ВВ1
49 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
в) А1B1+С1B1 +ВВ1
B1 С1
А1 D1

B С
А D
50 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
в) А1B1+С1B1 +ВВ1
B1 С1
А1 D1 Решение

А1B1+С1B1= D1 А1+ А1B1 = D1В1
D1В1 + ВВ1 = DВ + ВВ1 = DB1

B С Ответ : DB1
А D
51 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
г) A1 A+A1D1 +AВ
52 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
г) А1А+A1D1 +AВ
B1 С1
А1 D1

B С
А D
53 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
г) А1А+A1D1 +AВ
B1 С1
А1 D1 Решение

А1A+A1D1= A1D1+ D1D = A1D
A1D + AВ = A1D + DC = A1C

B С Ответ : A1C
А D
54 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
в) B1A1+BB1 +ВC
55 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
д) B1А 1 +BB1 +BC
B1 С1
А1 D1

B С
А D
56 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
д) B1А 1 +BB1 +BC
B1 С1
А1 D1 Решение

B1A 1 +BB1= BA1
BA1 + ВC = BA1 + A1D 1 = BD1

B С Ответ : BD1
А D
57 слайд

Решение задач
№ 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов :
в) B1A1+BB1 +ВC
58 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
а) АB +B1C1 +DD1+CD

B1 С1
А1 D1

B С
А D
59 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
а) АB +B1C1 +DD1+CD

B1 С1
А1 D1 Решение

AB +B1C1 = AB +BC = AC
AC + CD + DD1 = AD1

B С Ответ : AD1
А D
60 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
б) B1C1 + АB + DD1+CB1+ BC + AA1

B1 С1
А1 D1

B С
А D
61 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
б) B1C1 + АB + DD1+CB1+ BC + AA1

B1 С1
А1 D1 Решение

AB +B1C1 = AB +BC = AC
AC + CB1 = AB1
BC + AA1 = BA1 ; AB1 + BA1 = AC1
B С Ответ : AС1
А D
62 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
в) BА + АC + CB+DC + DA

B1 С1
А1 D1

B С
А D
63 слайд

Решение задач
№ 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов :
в) BА + АC + CB+DC + DA

B1 С1
А1 D1 Решение

DC+DA+BA +AC + CB = DB

B С Ответ : DB
А D
64 слайд

Решение задач
№ 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что
ОА1+ОВ1+ОС1=ОА+ОВ+ОС
65 слайд

Решение задач
№ 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что ОА1 +ОВ1+ОС1=ОА+ОВ+ОС
В

С1 А1

А В1 С
66 слайд

Решение задач
№ 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что ОА1 +ОВ1+ОС1=ОА+ОВ+ОС
В Доказательство ОС+СА1 =ОА1 ; ОА1 +А1В=ОВ;
СА1+А1В=1/2СВ, значит ОС — ОА1=ОА1-ОВ
отсюда следует, что ОС+ОВ=2ОА1
Аналогично, ОС+ОА=2ОВ1 и ОВ+ОА=2ОС1
С1 А1 Складывая почленно три полученные равенства, получим равенство, которое необходимо доказать.

А В1 С

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 267 013 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

Рейтинг:
2 из 5

13.04.2020
8512
1234

13.04.2020
260
6

13.04.2020
326
10

13.04.2020
2016
283

13.04.2020
483
5

13.04.2020
4179
588

13.04.2020
234
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс повышения квалификации «Методы и инструменты современного моделирования»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»

Источник

Геометрия, 10 класс

Урок №18. Компланарные векторы. Векторный метод решения задач

Перечень вопросов, рассматриваемых в теме:

— какие векторы называются компланарными и их изображение на чертежах

-определение компланарных векторов.

— признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

— основы векторного метода решения задач.

Основная литература:

Атанасян Л.С. и др. Геометрия. Учебник для 10-11классов — М.: Просвещение, 2017. C. 77-85.

Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь-конспект по геометрии для 10 класса. 2016. С.88-93.

Теоретический материал для самостоятельного изучения:

Давайте вспомним основные определения по теме «Векторы». В этом поможет следующее задание: установите соответствие между понятием и его определением.

Вектор		?
Равные векторы	Противоположно направлены и их длины равны.
Противоположные векторы	Направленный отрезок
Коллинеарные векторы	Сонаправлены и их длины равны.
Компланарные векторы	Лежат на одной или параллельных прямых

Появилось новое понятие о векторах в пространстве, которого не было на плоскости — компланарность векторов. С определения компланарных векторов и начинаются главные отличия векторов в планиметрии и стереометрии.

Компланарные векторы.

Определение2.Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Рассмотрим некоторые случаи:

1 случай. Любые два вектора всегда будут компланарными, ведь через них
можно провести прямые, а через две прямые всегда можно провести
единственную плоскость.

2 случай. Три вектора будут компланарными если среди них есть пара коллинеарных
векторов. Тогда через один из коллинеарных векторов и вектор не коллинеарный ему
можно провести плоскость. А для второго из коллинеарных векторов легко
изобразить равный в этой плоскости.

3 случай. Если хотя бы один из трёх векторов является нулевым, то эти три вектора компланарны

Из планиметрии: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Следующая теорема выражает признак компланарности трех векторов. Теорема (признак) Если вектор можно представить в виде = х + у, где х и у — некоторые числа, то векторы , и компланарны.

Для сложения трёх некомпланарных векторов можно пользоваться правилом параллелепипеда. Отложим от произвольной точки О векторы =, =, = и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были рёбрами.
Тогда ОD — диагональ этого параллелепипеда равна сумме векторов, и . Если вектор можно представить в виде суммы: = х + у + z, то говорят, что вектор d разложен по векторам , и . Числа х, у, z называют коэффициентами разложения.

Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Часть 2. Векторный метод решения задач

Векторный метод решения задач – один из наиболее общих методов решения геометрических задач. Векторное решение стереометрических задач значительно проще их решения средствами элементарной геометрии.

Рассмотрим следующую задачу: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

Пусть ABCD — данная трапеция, M и N — середины оснований BC И AD, а O — точка пересечения прямых AB и CD.

Докажем, что точка О лежит на прямой МN.

Условие задачи переводится на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык.

Решением задач векторным методом занимались ученые: Уильман Гамильтон Иога́нн Берну́лли, Пьер Ферма, Рене Декарт, Леонард Эйлер.

Примеры и разбор решения заданий тренировочного модуля:

Задача. В параллелепипеде АВСDА₁В₁С₁D₁ М —точка пересечения диагоналей грани A₁B₁C₁D₁, точка K — середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁ параллельны некоторой плоскости.

Решение. Введем векторы: . Векторы некомпланарны.

Разложим векторы и по векторам. Получим:

+= .

Тогда векторы = + компланарны. Следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А₁В₁, KМ и ВС₁.

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие компланарности векторов

Для начала рассмотрим, какие вектора называются компланарными.

Определение 1

Два вектора, которые параллельны одной плоскости называются компланарными.

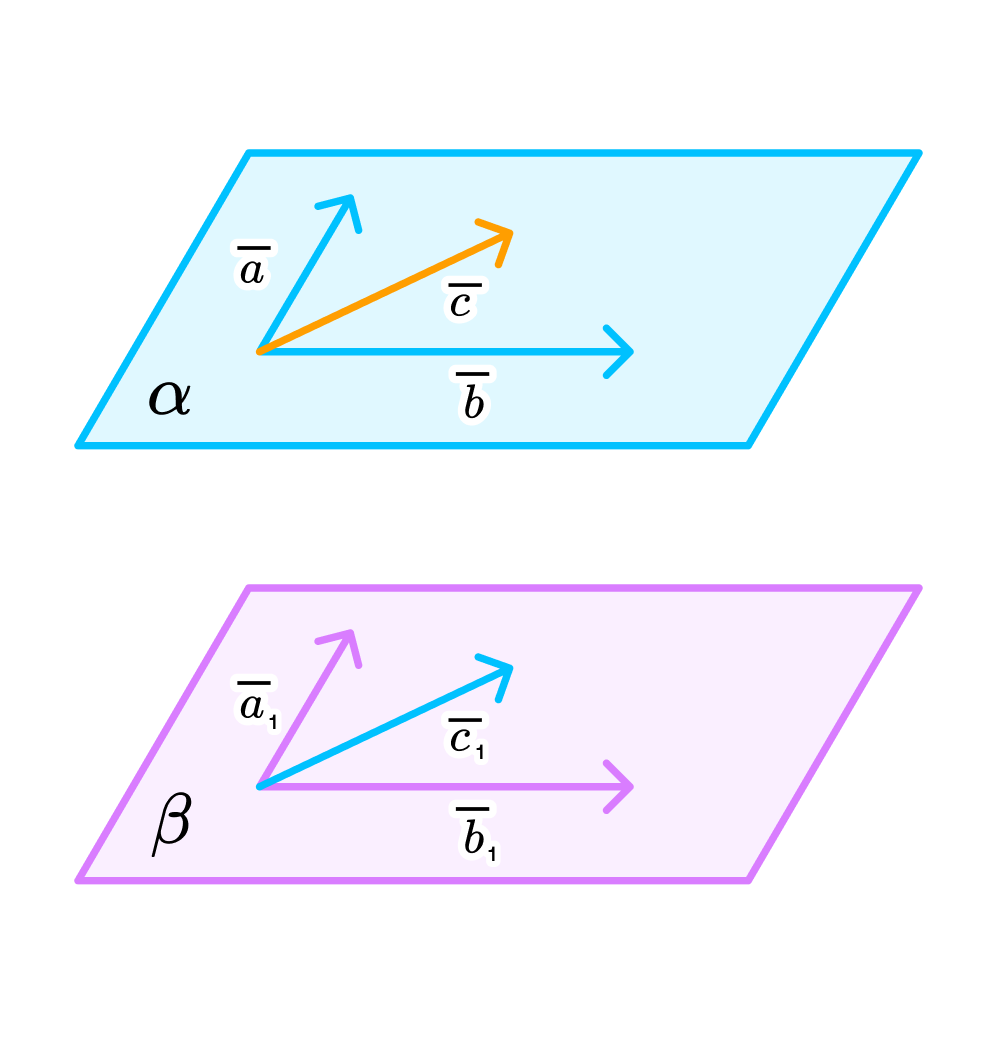
Рассмотри, компланарны ли векторы a, b и c на следующем примере. Пусть нам даны три вектора $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$. Тогда

Пары векторов $overrightarrow{a_1}, и overrightarrow{a_2}$, $overrightarrow{a_2}$ и $overrightarrow{a_3}$ и $overrightarrow{a_1}$ и $overrightarrow{a_3}$ компланарны между собой.
Если два из этих векторов, к примеру $overrightarrow{a_1}, и overrightarrow{a_2}$, коллинеарны, то векторы $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$ компланарны.
Если $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$ лежат в одной плоскости, то они компланарны.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Для дальнейшего рассмотрения напомним следующую теорему.

Произвольный вектор $overrightarrow{p}$ можно разложить по двум неколлинеарным векторам $overrightarrow{a_1}, $ и $overrightarrow{a_2}$ с единственными коэффициентами разложения, то есть

[overrightarrow{p}={alpha }_1overrightarrow{a_1}+{alpha }_2overrightarrow{a_2}]

Теоремы, связанные с условием компланарности трех векторов

Пусть нам даны три вектора $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$.

Теорема 2

Если один из трех данных векторов можно разложить по двум другим векторам, то есть

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

где $alpha $ и $beta $ — действительные числа, то векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ являются компланарными векторами.

Доказательство.

Здесь возможны два случая.

Векторы $overrightarrow{a} и overrightarrow{b}$ — коллинеарные векторы. Но это условие неприменимо, если одна из координат вектора приравнивается нулю.

В этом случае компланарность векторов $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ очевидна.
Векторы $overrightarrow{a} и overrightarrow{b}$ не являются коллинеарными.

Так как вектор $overrightarrow{c}$ имеет свое разложение по двум неколлинеарным векторам $overrightarrow{a} и overrightarrow{b}$. Значит эти векторы попадают под условие теоремы 1, и, следовательно, векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ лежат в одной плоскости, то есть являются компланарными.

Теорема доказана.

«Компланарные векторы» 👇

Теорема 3

Если три вектора $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ являются компланарными, а векторы $overrightarrow{a} и overrightarrow{b}$ не являются коллинеарными, то вектор $overrightarrow{c}$ можно единственным образом разложить по векторам $overrightarrow{a} и overrightarrow{b},$ то есть

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

Доказательство.

Так как векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ компланарны, то значит в произвольной плоскости $gamma $, которой параллельны эти векторы, можно построить векторы $overrightarrow{a’}=overrightarrow{a},$ $overrightarrow{b’}=overrightarrow{b}$ и $overrightarrow{c’}=overrightarrow{c}$. Так как векторы $overrightarrow{a} и overrightarrow{b}$ не коллинеарны, то и векторы $overrightarrow{a’}$ и $overrightarrow{b’}$ не коллинеарны, тогда, по теореме 1, вектор $overrightarrow{c’}$ можно разложить по векторам $overrightarrow{a’}$ и $overrightarrow{b’}$ следующим образом

[overrightarrow{c’}=alpha overrightarrow{a’}+beta overrightarrow{b’}]

Причем это разложение единственно.

Следовательно

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

Которое также единственно.

Теорема доказана.

Признак и критерий компланарности векторов

Пусть нам даны векторы $overrightarrow{a}=(a_1,a_2,a_3), overrightarrow{b}=(b_1,b_2,b_3)$ и $overrightarrow{c}=(c_1,c_2,c_3)$. Три вектора будут компланарны, если выполняется следующее условие:

компланарности векторов. Автор24 — интернет-биржа студенческих работ» />

Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ

Пример задачи

Пример 1

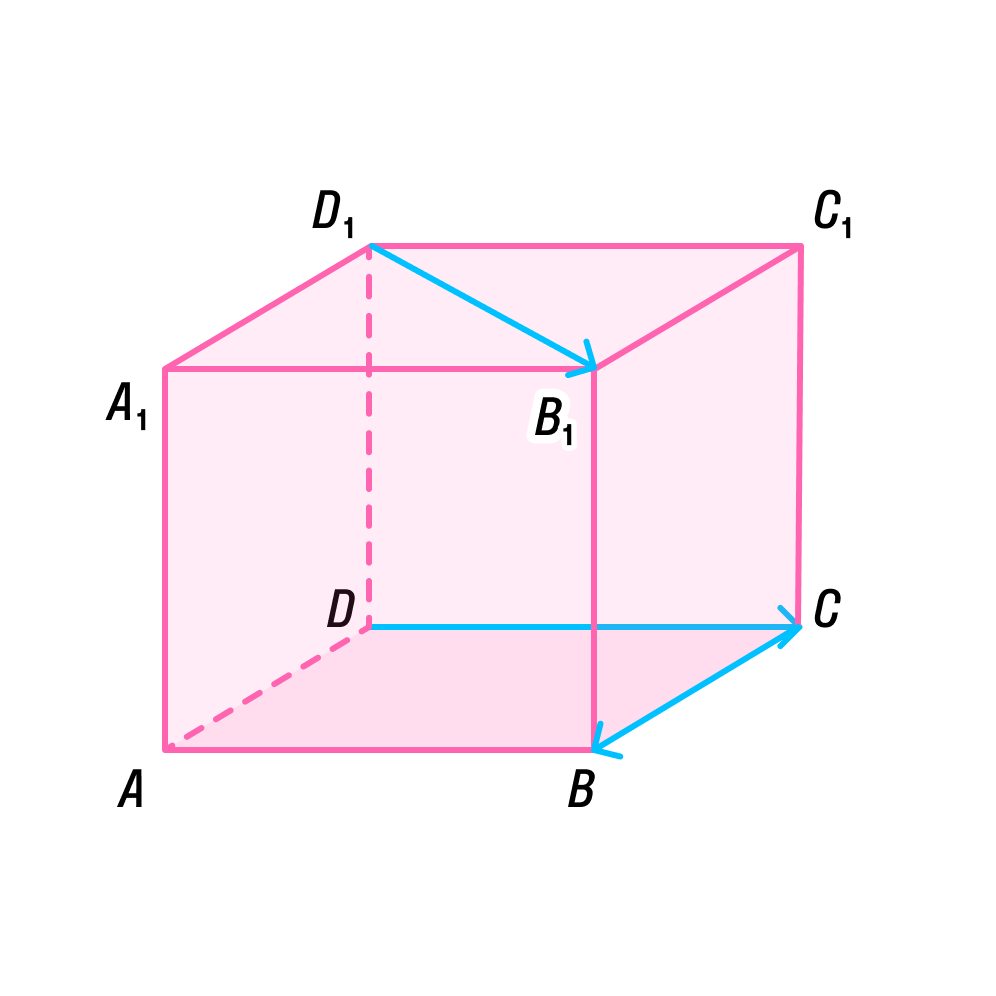
Пусть нам дан куб $ABCDA_1B_1C_1D_1$. Разложите вектор $overrightarrow{A_1C_1}$ по векторам $overrightarrow{AB} и overrightarrow{BC}$.

Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ

Решение.

Так как плоскости $(ABC)$ и ${(A}_1B_1C_1)$ параллельны, и векторы $overrightarrow{A_1C_1}$, $overrightarrow{AB} и overrightarrow{BC}$ параллельны, следовательно, по определению являются компланарными. Тогда, по теореме 1, вектор $overrightarrow{A_1C_1}$ можно разложить по векторам $overrightarrow{AB} и overrightarrow{BC}$ единственным образом.

Используя свойства сложения двух векторов, получим

[overrightarrow{A_1C_1}=overrightarrow{A_1B_1}+overrightarrow{B_1C_1}]

Так как

[overrightarrow{A_1B_1}=overrightarrow{AB}, overrightarrow{B_1C_1}=overrightarrow{BC}]

Следовательно

[overrightarrow{A_1C_1}=overrightarrow{AB}+overrightarrow{BC}]

Ответ: $overrightarrow{AB}+overrightarrow{BC}$.

Пример 2

Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.

Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

Так как векторы $overrightarrow{OA}, overrightarrow{OB}$ и $overrightarrow{OE}$ лежат в плоскости $(BOA)$ то эти векторы являются компланарными.
Так как векторы $overrightarrow{OC}, overrightarrow{OB}$ и $overrightarrow{{BB}_1}$ лежат в плоскости $(BOC)$ то эти векторы являются компланарными.
Так как векторы $overrightarrow{OC}, overrightarrow{OD}$ и $overrightarrow{OE}$ лежат в плоскости $(COE)$ то эти векторы являются компланарными.

Пример 3

Доказать, что векторы с координатами $left(1, 13, 2right), left(3, -5, 2right)и (5,-1,4)$ компланарны.

Решение.

Применим признак компланарности трех векторов.

Найдем определитель

Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ

Следовательно, это векторы компланарны, ч. т. д.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник