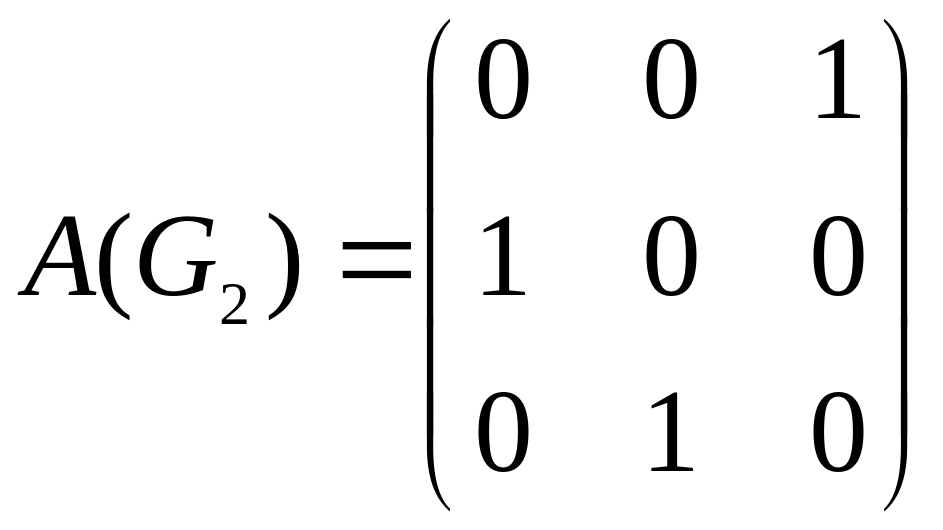Как найти компоненты связности в ориентированном графе

Поиск компонент сильной связности: алгоритм Косарайю

Время на прочтение
2 мин

Количество просмотров 33K

На хабре нет ни одной статьи о поиске компонент сильной связности. Однако это интересная задача, имеющая приложения в самых разных сферах: системах рекомендаций, математической логике и, неожиданно, экологии. Ниже формулировка задачи и решение — алгоритм Косарайю.

К делу:

Заметим: отношение сильной связности — это отношение эквивалентности.

$1)Рефлексивность: forall v v to v$

$2)Симметричность: forall v forall u v to u => u to v$

$3) Транзитивность: forall v forall u forall t v to u wedge u to t => v to t $

Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности.

Алгоритм Косарайю

  • Инвертированием ориентированного графа назовем процедуру, в ходе которой поменяем направление каждого ребра на противоположное.

Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования.

Пусть дан ориентированный граф G = (V, E). Через G’ = (V, E’) обозначим интертирование G.

Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0…|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1.


Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G’. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности.

Время работы

Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices.

Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices.

Дополнительно

Корректность алгоритма и псевдокод можно посмотреть тут: www.jeffreykarres.com/blog/kosaraju

В начале статьи я упоминал приложения.

  • На SO писали про использование этого алгоритма для формальной верификации:
    stackoverflow.com/questions/11212676/what-are-strongly-connected-components-used-for
  • А про экологию можно почитать в статье:
    www.nceas.ucsb.edu/~allesina/PDF/Allesina2005.pdf
Источник

Определение компоненты связности

Понятие компоненты связности вытекает из понятия связности графа. Попросту
говоря, компонента связности — часть графа (подграф), являющаяся связной.
Формально, компонента связности — набор вершин графа, между любой парой
которых существует путь.

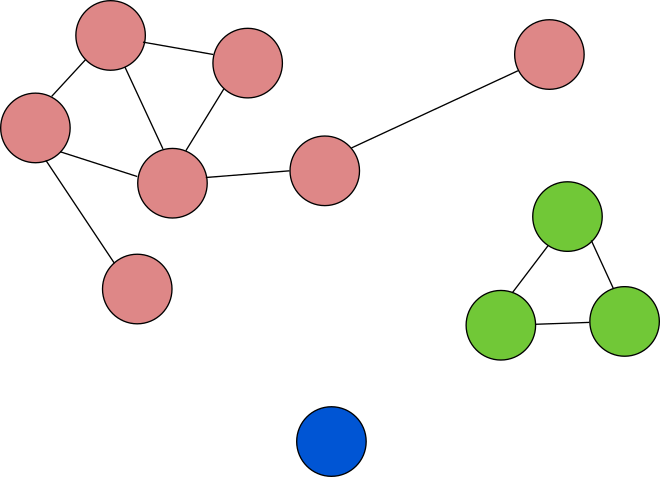
Граф с тремя компонентами связности

Граф на иллюстрации содержит три компоненты связности, закрашенные разными
цветами. Можно заметить, что даже одна вершина, изолированная от остального
графа, составляет компоненту связности.

Общее понятие связности распространяется только на неориентированные графы.
Для описания ориентированных графов используются понятия сильной и слабой
связности, но они выходят за границы материала этой лекции.

Алгоритм поиска компонент связности

Для поиска компонент связности используется обычный DFS практически без
модификаций (можно использовать и BFS). При запуске обхода из одной вершины, он
гарантированно посетит все вершины, до которых возможно добраться, то есть,
всю компоненту связности, к которой принадлежит начальная вершина. Для нахождения
всех компонент просто попытаемся запустить обход из каждой вершины по очереди,
если мы ещё не обошли её компоненту ранее.

Реализация

Приведём два варианта реализации с разным способом хранения компонент связности.

Простейший вариант: просто заполнить массив (comp), где (comp[i]) — номер
компоненты связности, к которой принадлежит вершина (i).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36





#include <bits/stdc++.h>

using namespace std;

vector<int> graph[100000];
bool used[100000];
int comp[100000];

void dfs(int v, int c_num) {    //c_num - номер текущей компоненты связности.
    used[v] = true;
    comp[v] = c_num;

    for (int u: graph[v]) {
        if (!used[u]) {
            dfs(u, c_num);
        }
    }
}

int main() {
    //Ввод графа...

    int c_num = 1;  //Номер очередной компоненты.
                    //Нумеровать можно как с 0, так и с 1, как вам удобнее.

    for (int i = 0; i < n; i++) {
        if (!used[i]) {     //если мы ещё не посетили эту вершину, обходя одну из предыдущих
            dfs(i, c_num);
            c_num++;
        }
    }

    for (int i = 0; i < n; i++) {
        cout << "Vertex " << i + 1 << " belongs to component " << comp[i] << endl;
    }
}











Другой вариант: явно хранить для каждой компоненты вектор из вершин, входящих

в неё. Компоненты (векторы) хранить в векторе (из векторов).


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40





#include <bits/stdc++.h>

using namespace std;

vector<int> graph[100000];
bool used[100000];

vector<vector<int>> comps;

void dfs(int v) {   //информацию о компоненте в DFS больше передавать не нужно,
                    //он просто будет добавлять вершины в последний вектор в comps.
    used[v] = true;
    comps.back().push_back(v);

    for (int u: graph[v]) {
        if (!used[u]) {
            dfs(u);
        }
    }
}

int main() {
    //Ввод графа...

    for (int i = 0; i < n; i++) {
        if (!used[i]) {
            comps.push_back(vector<int>());   //добавляем в comps новый пустой вектор,
                                              //в который DFS будет записывать посещённые вершины.
            dfs(i);
        }
    }

    for (vector<int>& comp: comps) {
        cout << "Component: ";
        for (int v: comp) {
            cout << v + 1 << ", ";
        }
        cout << endl;
    }
}
Источник

Содержание

  • 1 Случай неориентированного графа
  • 2 Случай ориентированного графа
    • 2.1 Слабая связность
    • 2.2 Сильная связность
  • 3 См. также
  • 4 Источники информации

Случай неориентированного графа

Определение:
Две вершины и называются связанными (англ. adjacent), если в графе существует путь из в (обозначение: ).
Определение:
Компонентой связности (англ. connected component) называется класс эквивалентности относительно связности.
Определение:
Граф называется связным (англ. connectivity graph), если он состоит из одной компоненты связности. В противном случае граф называется несвязным.

Случай ориентированного графа

В общем случае для ориентированного графа существование пути — не симметричное отношение, поэтому вместо понятия связности различают понятие слабой и сильной связности.

Слабая связность

Определение:
Отношение $R(v, u)$ называется отношением слабой связности (англ. weak connectivity), если вершины $u$ и $v$ связаны в неориентированном графе $G’$, полученном из графа $G$ удалением ориентации с рёбер.
Теорема:
Доказательство:
Аналогично доказательству соответствующей теоремы для неориентированного графа.

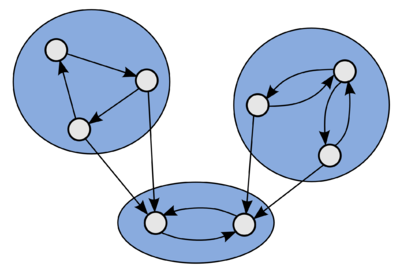
Пример ориентированного графа с тремя компонентами слабой связности.

Сильная связность

Определение:
Отношение на вершинах графа называется отношением сильной связности (англ. strong connectivity).
Определение:
Пусть — ориентированный граф. Компонентой сильной связности (англ. strongly connected component) называется класс эквивалентности множества вершин этого графа относительно сильной связности.

Компоненты сильной связности могут быть найдены с помощью обхода в глубину.

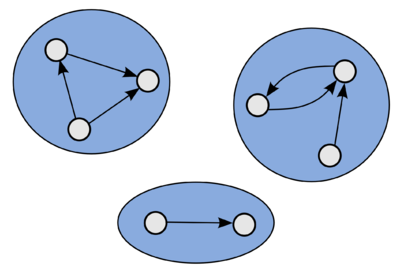
Пример ориентированного графа с тремя компонентами сильной связности.

Определение:
Ориентированный граф называется сильно связным (англ. strongly connected), если он состоит из одной компоненты сильной связности.

См. также

  • Отношение рёберной двусвязности
  • Отношение вершинной двусвязности

Источники информации

  • Отношения связности для вершин неорграфа на ivtb.ru
  • Харари Фрэнк Теория графов: Пер. с англ./ Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом «ЛИБРОКОМ», 2009. — 296 с. — ISBN 978-5-397-00622-4.
Источник

Неориентированный
граф называется связным,
если каждая пара различных вершин может
быть соединена, по крайней мере, одной
цепью.

Ориентированный
граф называется сильно
связным,
если для любых двух его вершин


и


существует
хотя бы один путь, соединяющий


с

.
Ориентированный граф называется
односторонне
связным,
если для любых двух его вершин, по крайней
мере, одна достижима из другой.

Компонентой
связности неориентированного графа
называется его связный подграф, не
являющийся собственным подграфом
никакого другого связного подграфа
данного графа (максимально связный
подграф).

Компонентой
сильной связности ориентированного
графа
называется его сильно связный подграф,
не являющийся собственным подграфом
никакого другого сильно связного
подграфа данного графа (максимально
сильно связный подграф).

Компонентой
односторонней связности ориентированного
графа называется
его односторонне связный подграф, не
являющийся собственным подграфом
никакого другого односторонне связного
подграфа данного графа (максимально
односторонне связный подграф).

Пусть

неориентированный граф с множеством
вершин

.
Квадратная матрица


порядка

,
у которой


называется
матрицей
связности графа

.

Для ориентированного
графа квадратная матрица

порядка

,
у которой

называется
матрицей
односторонней связности (достижимости).

Квадратная матрица

порядка

,
у которой

называется матрицей
сильной связности.

Пример. У
неориентированного графа, изображенного
на рис. 22 две компоненты связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

.

Рис. 22. Компоненты
связанности неориентированного графа

Матрица связности
этого графа имеет вид:

.

Мы видим, что 1-ая,
2-ая, 4-ая и 5-ая строки матрицы

одинаковы.

Пример. У
ориентированного графа, изображенного
на рис. 23 две компоненты сильной связности.
Первая компонента связности включает
вершины

,
а вторая
состоит из одной вершины

.
Действительно, для любой пары вершин
из множества


существует
хотя бы один путь, соединяющий эти
вершины. Например, путь

соединяет все эти вершины. Из вершины

нет пути ни в одну вершину графа.

Рис. 23. Компоненты
сильной связанности ориентированного
графа

Матрица сильной
связности этого графа имеет вид:


.

Заметим, что 1-ая,
2-ая, 3-ая и 5-ая строки матрицы

одинаковы.

Для того, чтобы
выделить компоненты сильной связности,
необходимо сначала найти матрицу
достижимости

ориентированного графа, затем находим
матрицу сильной связности

ориентированного графа (она должна быть
симметрической).

Алгоритм выделения
компонента сильной связности:

1. Присваиваем

(

− количество компонент связности),


.

2. Включаем в
множество вершин


компоненты
сильной связности

вершины, соответствующие единицам
первой строки матрицы

.
В качестве матрицы смежности

возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

.

3. Вычеркиваем из

строки и столбцы, соответствующие
вершинам из

.
Если не остается ни одной строки (и
столбца), то


количество компонент сильной связности.
В противном случае обозначим оставшуюся
после вычеркивания срок и столбцов
матрицу как

,
присваиваем

и переходим к п. 2.

Пример. Выделим
компоненты связности ориентированного
графа, изображенного на рис. 25. Количество
вершин

.

Рис. 25.

Значит, для данного
ориентированного графа матрица смежности
будет иметь размерность

и будет выглядеть следующим образом


.

Найдем матрицу
достижимости и матрицу сильной связности
для данного ориентированного графа:


,


.

Присваиваем

,

и составляем множество вершин первой
компоненты сильной связности

:
это те вершины, которым соответствуют
единицы в первой строке матрицы

.
Таким образом, первая компонента сильной
связности состоит из одной вершины

.

Вычеркиваем из
матрицы

строку и столбец, соответствующие
вершине

,
чтобы получить матрицу

.

Присваиваем

.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы

,
то есть

.
Составляем матрицу смежности для
компоненты сильной связности

исходного графа


− в ее
качестве возьмем подматрицу матрицы

,
состоящую из элементов матрицы

,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из

:


.

Вычеркиваем из
матрицы

строки и столбцы, соответствующие
вершинам из

,чтобы
получить матрицу

,
которая состоит из одного элемента

,
присваиваем

.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины

.

Таким образом,
выделены 3 компоненты сильной связности
ориентированного графа

:

:


:


:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

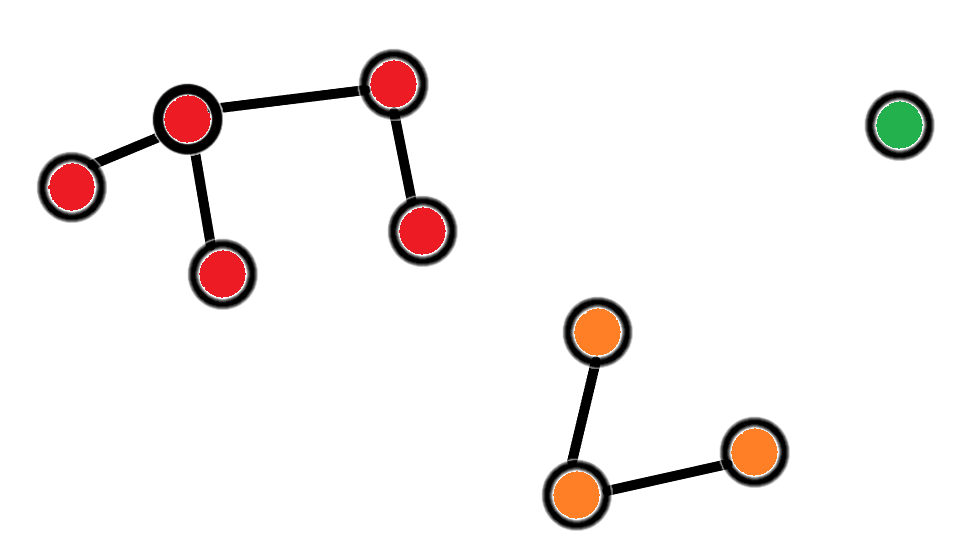
Компонента связности — набор вершин графа, в котором между любой парой вершин существует путь. В свою очередь одна вершина тоже составляет компоненту связности.

На данном изображении три компоненты связности
component

Определение, данное нами выше, распространяется на неориентированные графы. Для ориентированных графов применяют такие понятия как слабая и сильная связность. В данной статье данные эти понятия рассматриваться не будут.

Алгоритм

Как найти компоненты связности?

Для этого нам нужно использовать один из двух методов обхода графа (BFS / DFS). При запуске обхода из одной вершины, он гарантированно посетит все вершины, до которых возможно добраться, то есть, всю компоненту связности, к которой принадлежит начальная вершина. Для нахождения всех компонент просто попытаемся запустить обход из каждой вершины по очереди, если мы ещё не обошли её компоненту ранее.

Каждую компоненту связности будем нумеровать, для чего создадим массив компонент (comp).

bool used[100];
vector <vector<int>> graph(100);
int comp[100];

void dfs(int vertex, int components)
{
	used[vertex] = true;
	comp[vertex] = components;
	for (auto u : graph[vertex])
	{
		if (!used[u])
			dfs(u, components);
	}
}

int main()
{
	int n,m;
	int components = 1; // нумеруем компоненты с 1
	cout << "Enter the number of edges: ";
	cin >> n;
	cout << "Enter the number of vertexes: ";
	cin >> m;
	for (int i = 0; i < n; i++)
	{
		int a, b;
		cin >> a >> b;
		graph[a].push_back(b);
		graph[b].push_back(a);
	}

	for (int i = 1; i <= m; i++) {
		if (!used[i]) {     //если мы ещё не посетили эту вершину, обходя одну из предыдущих
			dfs(i, components);
			components++;
		}
	}
	for (int i = 1; i <= m; i++) {
		cout << "Vertex " << i << " belongs to component #" << comp[i] << endl;
	}
	return 0;
}

Таким образом, мы можем узнать, что такая вершина принадлежит такой-то компоненте связности.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти видео в кэше телефона
  • Как найти друга корейца по переписке
  • Код ошибки 0x80040154 0x90018 windows 10 как исправить
  • Как найти модем yota в диспетчере устройств
  • Как найти сайт друга в одноклассниках