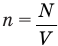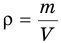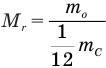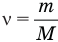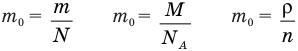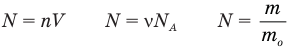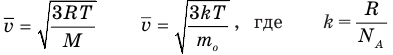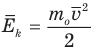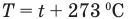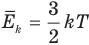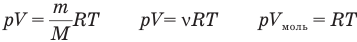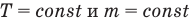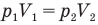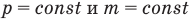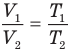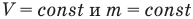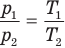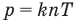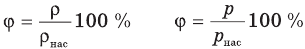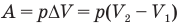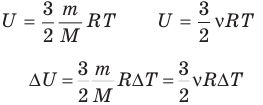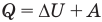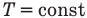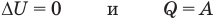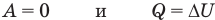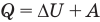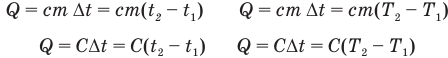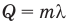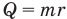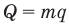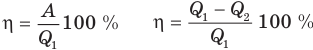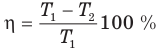Переведем величины из дано в систему СИ:
Р=1,38 МПа = 1,38 *10^6 Па.
Воспользуемся уравнением Менделеева — Клапейрона:
P=n*k*T , где n — концентрация газа, k — постоянной Больцмана k=1,38*10^-23, T — температура газа.
Выразим из этого выражения концентрацию:
n=Р/(k*T)
Подставим числовые значения и вычислим концентрацию:
n=Р/(k*T)=1,38*10^6/(1,38*10^-23*100)=1*10^27 1/м³.
Ответ: концентрация газа 1*10^27 1/м³.
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 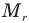

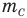
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 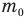
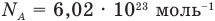



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

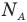
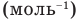

Формулы средней квадратичной скорости молекул
Здесь 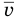
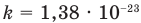

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

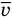

Формула средней кинетической энергии молекул
Здесь 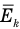
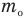
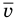
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
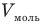
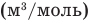
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 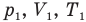

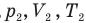

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 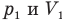

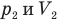

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 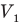
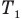

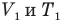

Закон Шарля
при
Здесь V — объем газа 
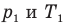
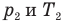
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 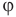
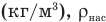
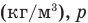
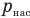
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 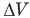
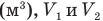

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 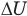
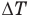
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
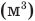
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 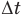
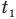
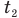
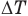
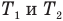
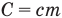
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 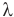
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
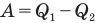
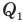
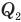
Коэффициент полезного действия идеального теплового двигателя
Здесь 
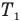
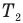
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Концентрация частиц – это величина, показывающая, сколько частиц вещества находится в каком-либо объеме. Она вычисляется по формуле: c = N/V, ее размерность 1/м^3. Часто возникает необходимость определить концентрацию молекул, причем исследуемое вещество может быть в любом агрегатном состоянии: твердом, жидком или газообразном.
Представьте, что любознательный царь Гиерон дал своему придворному математику еще одну корону, приказав: «Вот она-то точно из чистого золота. Определи, Архимед, какова концентрация молекул в ней». Гениального ученого такая задача поставила бы в тупик. Ну, а вы решите ее очень быстро. Предположим, корона весила бы ровно 1,93 килограмма, занимая при этом объем в 100 см^3.
Прежде всего найдите, сколько молей золота содержится в таком количестве вещества. С помощью таблицы Менделеева вы узнаете молекулярную массу золота: 197 а.е.м. (атомных единиц массы). А масса одного моля любого вещества (в граммах) численно равна его молекулярной массе. Следовательно, один моль золота весит 197 грамм. Разделив фактическую массу короны на молярную массу золота, вы получите: 1930/197 = 9,79. Или, округленно, 9,8 молей золота.
Умножьте количество молей на универсальное число Авогадро, показывающее, сколько элементарных частиц содержится в моле любого вещества. 9,8*6,022*10^23 = 5,9*10^24. Вот сколько молекул золота приблизительно содержится в короне.
Ну, а теперь найти концентрацию молекул проще простого. 100 кубических сантиметров – это 0,0001 м^3. Разделим: 5,9*10^24/0,0001 = 5,9*10^28. Концентрация молекул золота равна 5,9*10^28/м3.
Теперь предположим, что вам задана такая задача: при давлении Р, средняя квадратичная скорость молекул углекислого газа равна V. Требуется определить концентрацию его молекул. И здесь нет ничего сложного. Существует так называемое основное уравнение кинетической теории идеального газа: Р = V^2m0C/3, где C – концентрация молекул газа, а m0 – масса одной его молекулы. Следовательно, искомая концентрация С находится так: С = 3P/m0V^2.
Единственная неизвестная величина – m0. Ее можно узнать в справочнике по химии или физике. Можно также вычислить по формуле: m0 = M/Na, где М – молярная масса углекислого газа (44 грамм/моль), а Na – число Авогадро (6,022х1023). Подставив все величины в формулу, вычислите искомую концентрацию С.
Видоизмените условие задачи. Предположим, вам известны только температура Т и давление Р углекислого газа. Как по этим данным найти концентрацию его молекул? Давление и температура газа связаны формулой: P = CkT, где С – концентрация молекул газа, а К – постоянная Больцмана, равная 1,38*10^-23. То есть С = P/kT. Подставив в формулу известные величины, вы вычислите концентрацию С.
Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.
Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
P*V = n*R*T.
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R — это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление
Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
cN = N/V.
Где N — общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
n = N/NA;
kB = R/NA.
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
P*V = n*R*T =>
P*V = N/NA*R*T = N*kB*T =>
cN = N/V = P/(kB*T).
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
cn = n/V = P/(R *T).
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.
Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 oC (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
cn(O2) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м3.
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*1021 молекул.
Способы представления концентрации газа
В
некоторых моделях мониторов предусмотрена
возможность выбора единиц измерения
содержания СО2
в газовой смеси (кПа, мм рт. ст , %). Между
способами отображения информации есть
не формальное, а весьма существенное
различие.
Относительная
концентрация газа измеряется
в объемных процентах (%). Так, концентрация
СО2,
равная 5 %, означает, что в 100 мл газовой
смеси содержится 5 мл углекислого газа.
Относительная
концентрация, выраженная десятичной
дробью, называется «фракционной
концентрацией», или «фракцией газа
в газовой смеси». Например, фракция
кислорода, равная 0,21, — это то же, что
концентрация кислорода, равная 21 %.
Относительная
концентрация — самый традиционный, но
не самый удачный способ отображения
содержания газа в газовой смеси. Дело
в том, что при изменении атмосферного
давления газ становится либо более
плотным, либо более разреженным, и хотя
процентные соотношения компонентов
газовой смеси при этом остаются прежними,
количество молекул газа в каждом проценте
изменяется, а соответственно, изменяется
и эффективность альвеолярной вентиляции.
Кроме того, выражение концентрации в
процентах оказывается крайне неудобным,
когда требуется сравнить содержание
СО2
в выдыхаемом газе с напряжением СО2
в крови. И, наконец, хеморецепторы
организма не понимают, что такое
относительная концентрация, и упрямо
ориентируются на концентрацию абсолютную.
В
физиологии дыхания объемная концентрация
газа обозначается знаком F,
за которым следуют подстрочный индекс,
обозначающий газовую смесь (I
— вдыхаемый газ, Е — выдыхаемый, А —
альвеолярный, ЕТ — конечная часть
выдыхаемого газа и пр.), и формула самого
газа.
Например,
FiCO21
— это процентное содержание углекислого
газа во вдыхаемом газе; FETCO2
читается как «процентная концентрация
углекислого газа в конечной порции
выдыхаемого газа», a
FiO2
— это фракция кислорода во вдыхаемом
газе.
Процентный состав
газовой смеси определяют с помощью
масс-спектрометров.
1В
соответствии со стандартами филиологии,
формула газа должна обозначаться и виде
подстрочного индекса, но на практике
это правило оказалось настолько
неудобным, что в последние годы его не
выполняют даже профессиональные журналы.
Парциальное
давление газа в
газовой смеси (от лат. pars
— часть)
измеряется в миллиметрах ртутного
столба (мм рт.ст.) или в килопаскалях
(кПа), на которые уже не первое десятилетие
лениво пытается перейти весь мир.
Парциальное
давление газа — это та часть общего
барометрического давления, которая
обеспечивается молекулами данного
компонента газовой смеси.
На каждый газ в
смеси приходится часть барометрического
давления, соответствующая объемной
концентрации этого газа. Поэтому сумма
парциальных давлений всех компонентов
газовой смеси равна барометрическому
давлению (закон Дальтона).
В
физиологии дыхания парциальное давление
обозначается символом Р (от англ.,
pressure
— давление), за которым следуют индекс
газовой смеси и формула самого газа.
Так,
РETСO2
— это парциальное давление углекислого
газа в конечной части выдыхаемого газа,
а РAСO2
— парциальное давление СО2
в альвеолярном газе.
Например, если
вдыхаемый газ содержит 30 % кислорода,
68 % закиси азота и 2 % фторотана (галотана),
а атмосферное давление равно 760 мм рт.
ст., то
РIО2
= (760 х 30 %) — 228 мм рт. ст.
PIN2O
=(760X68%) — 516,8 мм рт. ст.
PIHAL
=(760х 2%) = 15,2 мм рт. ст.
Итого: 100% = 760 мм
рт. ст.
Зная величину
атмосферного давления и парциального
давления газа, легко вычислить его
процентную концентрацию:
Относительная
концентрация газа (%) =
Парциальное
давление газа (мм рт. ст.)
=
———————————————————————
100%
Барометрическое
давление (мм рт. ст.)
Парциальное
давление — это один из показателей
абсолютной
концентрации, то
есть количества молекул газа в единице
объема газовой смеси. При этом концентрация
газа выражается через давление, которое
обеспечивают его молекулы. Чем больше
молекул газа в единице объема, тем выше
парциальное давление этого газа.
При колебаниях
атмосферного давления соответственно
изменяются и парциальные давления
газов, отражая изменения их абсолютных
концентраций, хотя процентные соотношения
компонентов смеси остаются прежними.
Если в рассмотренном
нами примере атмосферное давление
снижается с 760 до 730 мм рт. ст., то парциальные
давления газов также уменьшатся:
PIO2
= (730 X 30%) = 219 мм рт. ст.
PIN2O
— (730 X 68 %) — 496,4 мм
рт.
PIHAL
=(730x 2%) = 14,6 мм
рт.
ст.
Итого: 100% = 730 мм
рт. ст.
Исчисление
концентрации газа в единицах давления
удобно тем, что предоставляет возможность
сравнивать парциальное давление газа
в газовой смеси (например, в альвеолярном
или вдыхаемом газе) с напряжением этого
газа в крови или в тканях и тем самым
определять градиент давлений, от которого
зависят направление и скорость газообмена
в легких и в тканях.
Инфракрасные
капнографы измеряют абсолютные
концентрации углекислого газа и
летучих анестетиков и выражают их в мм
рт. ст. или в кПа. Процентная концентрация
газа, высвечиваемая на дисплее, всегда
является расчетной величиной, для
получения которой программа монитора
оперирует данными встроенных барометра
и термометра.
При использовании
данных капнографии следует иметь в виду
еще одно обстоятельство. На величину
реального парциального давления
углекислого газа влияют пары воды,
которыми насыщен альвеолярный газ.
Парциальное давление воды при 37 °С
составляет 47 мм рт.ст., а на долю остальных
компонентов альвеолярного газа приходится
760-47 = 713 мм рт. ст. Поэтому парциальному
давлению СО2 в альвеолах, равному
40 мм рт. ст., соответствует концентрация
этого газа, составляющая
РAСО2
= 40/713 х 100 = 5,6 %.
Перед
поступлением в измерительную камеру
капнографа проба газа искусственно
обезвоживается. При исчезновении любого
из компонентов газовой смеси относительные
концентрации всех других повышаются.
В связи с тем, что капнографы калибруются
сухими газами, поправка, связанная с
изменением влажности, не вносится, и
программное обеспечение капнографа
производит пересчет парциального
давления в процентную концентрацию,
исходя из условий измерения,
а не из
условий альвеолярной среды. Например,
если измеренное парциальное давление
СО2
равно 35 мм рт. ст., то при атмосферном
давлении 760 мм рт. ст. рассчитанная
капнографом относительная концентрация
углекислого газа составит
РетСО2
= 35/760 X
100 = 4,6 %.
Несоответствие
между измеренной и реальной величинами
РETСO2
равно нескольким мм рт. ст. и в клинической
практике обычно не берется во внимание.
В капнографах,
имеющих встроенный барометр, поправка
на колебания атмосферного давления
производится автоматически.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #