UptoLike
Концентрация молекул – это физическая величина, равная числу молекул, содержащихся в единице объема.
Единицы измерения в системе СИ: [n] = 1/м3.
Формула концентрации молекул:
[n = frac{N}{V}]
где
N — число молекул;
V – объем, м3.
Тематические задачи
Определить концентрацию n молекул кислорода, находящегося в сосуде объемом V = 2 л. Количество вещества кислорода равно ν = 0,2 моль.
Определить количество вещества ν водорода, заполняющего сосуд объемом V = 3 л, если концентрация молекул газа в сосуде n = 2∙1018 м-3.
В баллоне объемом V = 3 л содержится кислород массой m = 10 г. Определить концентрацию n молекул газа.
[13.11.2015 16:45]
Решение 13471:
Номер задачи на нашем сайте: 13471
ГДЗ из решебника:
Тема:
2. Молекулярная физика. Термодинамика
Контрольная работа 2.
Нашли ошибку? Сообщите в комментариях (внизу страницы)
|
Раздел: Физика Полное условие: 206. Определить концентрацию n молекул кислорода, находящегося в сосуде вместимостью V=2 л. Количество вещества ν кислорода равно 0,2 моль.Решение, ответ задачи 13471 из ГДЗ и решебников: Этот учебный материал представлен 1 способом:
|
||
| Счетчики: 4632 | Добавил: Admin |
| Добавить комментарий
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
Решение.
Концентрацию молекул кислорода определим по формуле:
[ p=ncdot kcdot T,n=frac{p}{kcdot T}(1).n=frac{{{10}^{5}}}{1,38cdot {{10}^{-23}}cdot 273}=2,654cdot {{10}^{25}}. ]
Где: р –давление кислорода при нормальных условиях, р = 105 Па, Т – температура кислорода при нормальных условиях, Т = 273 К, k – постоянная Больцмана, k = 1,38∙10-23 Дж/К.
Определим количество молекул кислорода, количество вещества и массу кислорода
[ begin{align}
& n=frac{N}{V},N=ncdot V(2),,nu =frac{N}{{{N}_{A}}},nu =frac{ncdot V}{{{N}_{A}}}(3),nu =frac{m}{M},m=nu cdot M(4). \
& nu =frac{2,654cdot {{10}^{25}}cdot 2,24cdot {{10}^{-3}}}{6,02cdot {{10}^{23}}}=0,09875.m=0,09875cdot 32cdot {{10}^{-3}}=3,16cdot {{10}^{-3}}. \
end{align} ]
M – молярная масса молекулы кислорода, М = 32∙10-3 кг/моль, NА = 6,02∙1023 моль-1 – число Авогадро.
Ответ: 2,654∙1025 м-3, 0,09875 моль, 3,16 г.
План решения задач на газовые законы
-
Если
в задаче рассматривается одно состояние
газа и требуется найти какой-либо
параметр этого состояния, нужно
воспользоваться уравнением Менделеева
– Клапейрона. -
Если
значения давления и объема явно не
заданы, их нужно выразить через заданные
величины, подставить в записанное
уравнение и, решив его, найти неизвестный
параметр. -
В
том случае, когда в задаче рассматриваются
два различных состояния газа, нужно
установить, изменяется ли масса газа
при переходе из одного состояния в
другое. Если масса остается постоянной,
можно применить уравнение Клапейрона.
Если же при постоянной массе в данном
процессе не изменяется какой-либо из
параметров ( р,V или Т), применяются
уравнение соответствующего закона
(Гей-Люссака, Шарля или Бойля-Мариотта). -
Если
в двух состояниях масса газа разная,
то для каждого состояния записывают
уравнение Менделеева-Клапейрона. Затем
систему уравнений решают относительно
искомой величины.
Примеры решения задач
Пример 3.1. Определите
число молекул воды в бутылке вместимостью
0,33л. Молярная масса воды М=18∙10-3
кг/моль, плотность воды ρ=1г/см3.
Дано:
V=0,33л=0,33∙10-3
м3;
М=18∙10-3
кг/моль; ρ=1г/см3=
1∙103
кг/м3;
Найти:
N.
Решение:
Масса
воды, занимающей объём V,
m=ρV,
(1)
где
ρ – плотность воды.
Масса
молекулы
,
(2)
где
М – молярная масса; NA=6,02∙
1023моль-1
–
постоянная Авогадро.
Число
молекул в бутылке
(3)
Подставляя
в выражение (3) формулы (1) и (2), получим
искомое число молекул:
.
Ответ:
N=1,1∙1025.
Пример 3.1. Узкая
цилиндрическая трубка, закрытая с одного
конца, содержит воздух, отделённый от
наружного воздуха столбиком ртути.
Когда трубка обращена закрытым концом
кверху, воздух внутри неё занимает длину
ℓ, когда же трубка обращена кверху
открытым концом, то воздух внутри неё
занимает длину ℓ’ < ℓ. Длина ртутного
столбика h мм. Определить атмосферное
давление.
Дано:
ℓ; ℓ’ < ℓ; h.
Найти:
Р.
Решение:
В данном процессе
изменяются давление и объём воздуха, а
температура остаётся постоянной.
Следовательно, если начальные параметры
воздуха обозначить Р1
и V1,
а конечные как Р2
и V2 получаем
следующее соотношение:
Р1V1
= Р2V2
Когда
трубка обращена закрытым концом кверху,
воздух в ней находится под давлением
Р1=
Ратм
– h ( здесь и далее измеряем в мм.рт. ст.).
Если же трубку перевернуть, давление
воздуха в ней будет равно Р2
= Ратм
+ h .
Учитывая,
что V1 =
Sℓ1,
V2 =
Sℓ2,
где S — площадь сечения трубки, получаем:
(Ратм
– h) Sℓ =
(Ратм
+ h) Sℓ’,
Отсюда
находим атмосферное давление
Ответ.
Пример
3.2. В сосуде находится
смесь m = 7 г азота и m = 11г углекислого
газа при температуре Т = 290 К и давлении
Р = 1 атм. Найти плотность этой смеси,
считая газа идеальными.
Дано:
m1=7
г=7∙10-3кг;
m2=11
г=11∙10-3кг;
Т=290К; Р=1атм=105Па.
Найти:
ρ.
Решение:
Давление газов в сосуде
известно. Если через Р1
обозначить давление
азота, если бы углекислого газа не было,
а через Р2 давление
углекислого газа, если бы не было азота
(так называемые парциальными давления),
то давление смеси газов Р будет согласно
закону Дальтона Р =
Р1 +
Р2.
Учитывая, что температура каждого газа
Т запишем для азота и кислорода уравнение
Менделеева-Клапейрона:
Складывая
эти выражения, получаем:
Отсюда
находим объём, занимаемый смесью газов
Плотность
смеси газов вычисляется по формуле
Ответ:
Пример
3.3. Кислород массой
m=10г
находится под давлением 200кПа при
температуре 280К. В результате изобарного
расширения газ занял объём 9л. Определите:
1) объём газа V1
до расширения; 2) температуру газа T2
после расширения; 3) плотность газа ρ2
после расширения.
Дано:
M=32∙10-3кг/моль;
m=10г=10∙10-3кг;
р=200кПа=2∙105Па=const;
Т1=280К;
V2=9г=9∙10-3м3.
Найти:
1) V1;
2) Т2;
3) ρ2.
Решение:
Объём газа до расширения найдём, согласно
уравнению Клапейрона-Менделеева,
,
откуда
Записав уравнение Клапейрона-Менделеева
для конечного состояния газа:
,
найдём искомую температуру
Плотность газа после расширения газа
.
Ответ:
1) V1=3,64
л; 2) Т2=693
К; 3) ρ2=1,11
кг/м3.
Пример 3.3. В
цилиндре с площадью основания 100 см2
находится воздух. Поршень расположен
на высоте 50 см от дна цилиндра. На поршень
кладут груз массой 50 кг, при этом он
опускается на 10 см. Найти температуру
воздуха после опускания поршня, если
до его опускания давление было равно
101 кПа, а температура 12С.
Дано: S=100см2=1∙10-2м2;h1=50см=0,5
м;m=50кг; Δh=10см=0,1
мt;P1=101∙103Па; Т1=12С=285
К.
Найти:
Т2.
Решение:
Рассмотрим два состояния воздуха под
поршнем: до опускания поршня и после
его опускания. До опускания поршня
состояние воздуха характеризуется
параметрами Р1,
V1,
T1,
после опускания поршня – параметрами
Р2,
V2,
T2,
где V1=Sh1,
Р2=Р0+Р,
,
V2=Sh2,
или, поскольку h2=h1—
Δh,
V2=S(h1—
Δh).
Применим
к этим двум состояниям формулу Клапейрона:
,
откуда
(1)
Подставим
в формулу (1) выражения для Р1,
V1,
Р2
и V2:

Ответ:
Т2=338К
Пример 3.3. Имеются
два сосуда с газом: один вместимостью
3 л, другой 4 л. В первом сосуде газ
находится под давлением 202 кПа, а во
втором 101 кПа. Под каким давлением будет
находиться газ, если эти cосуды соединить
между собой? Считать, что температура
в сосудах одинакова и постоянна.
Дано: V1=3л=3∙10—3м3;V2=4л=4∙10—3м3;Р1=202кПа=202∙103Па; Р2=101кПа=101∙103Па.
Найти:
Р.
Решение:
По закону Дальтона,
Р
= Р3
+ Р4 (1)
Так
как процесс изотермический, то парциальное
давление газа в каждом сосуде можно
найти по закону Бойля-Мариотта:
Р1V1
=
Р3V,
Р2V2
=
Р4V,
где
V=V1+V2.
Тогда парциальное давление газа в каждом
из сосудов после их соединения
,
, (2)
Подставляем
выражения (2) в (1):
Ответ:
Р=141 Па
Пример 3.3. В
баллоне содержатся сжатый газ при
температуре t1
= 27С
и давлении p1
= 4 МПа. Каково будет давление, если из
баллона выпустить
Δm
= 0,4m
массы газа, а температуру понизить до
t2
= 17С?
Дано: Т1=27С
=300 К;Р1=4МПа=4∙106
Па;Δm
= 0,4m;
Т2=17С
=290 К Найти:
Р.
Решение: Рассмотрим
два состояния газа: до разрежения и
после, когда осталось1-n массы m газа.
Параметры каждого из этих состояний
связаны уравнением Менделеева-Клапейрона:
,
где
Р1,
Т1,
Р2,
Т2
– соответственно давление и температура
газа до и после выпуска; m — масса газа;
М – молярная масса; V — объем.
Разделив
почленно первое равенство на второе,
получим:
,
oткуда
(1)
Ответ:
Р2
= 2,3106
Па = 2,3 МПа.
Пример
3.3. Найти максимально
возможную температуру идеального газа
в процессе P = P0
– αV2,
где P0,
α — положительные постоянные.
Дано:
P = P0
– αV2;
P0, α
— const
Найти:
Tmax.
Решение:
Для нахождения максимальной температуры
необходимо получить явную зависимость
последней от параметров и исследовать
эту зависимость на экстремум. Так как
газ является идеальным, выразим давление
из уравнения Менделеева-Клапейрона и
подставим его в уравнение процесса
Отсюда
выражаем температуру
Условие экстремума
,
которое сводится к выражению.
Решая
данное уравнение, получаем значение
объёма, при котором температура принимает
экстремальное значение
.
Исследуя знак второй производной, приходим к выводу, что при данном
значении объёма температура газа будет
идеальной. Подставляя выражение для
объёма в выражение для температуры при
данном процессе, получаем:
Ответ:
Пример
3.3. В сосуде
вместимостью V=5л
находится кислород массой m=15г.
определите: 1) концентрацию молекул
кислорода в сосуде; 2) число N
молекул газа в сосуде.
Дано:
V=5л=5∙10-3м3;
M=32∙10-3кг/моль;
m=15г=1,5∙10-2кг.
Найти:
1) n; 2) N.
Решение:
Записав
уравнение Клапейрона-Менделеева
(1)
И
уравнение состояния идеального газа
Р=nkT
(2)
И
поделив (1) на (2), найдём искомую концентрацию
молекул кислорода в сосуде
.
Концентрация
молекул
,
Откуда
искомое число молекул газа в сосуде
N=nV.
Ответ:
1)
n=5,64∙1025
м-3;
2) N=2,82∙1023.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
Определить концентрацию n молекул кислорода, находящегося в сосуде объемом V = 2 л.
Количество вещества n кислорода равно 0.
2 моль.
На странице вопроса Определить концентрацию n молекул кислорода, находящегося в сосуде объемом V = 2 л? из категории Физика вы найдете
ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.

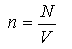

 Для просмотра в натуральную величину нажмите на картинку
Для просмотра в натуральную величину нажмите на картинку

