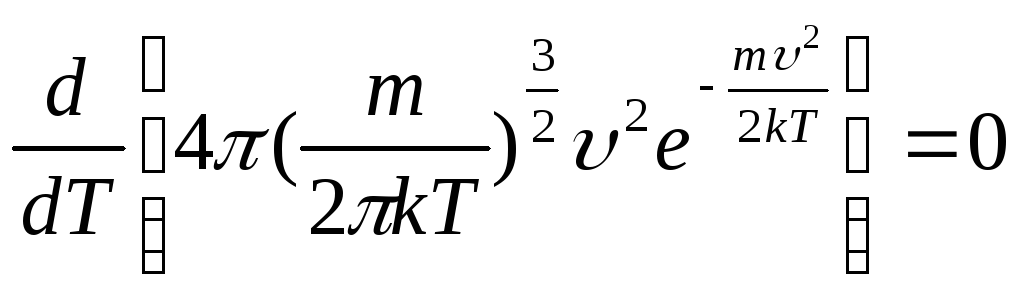Как найти концентрацию молекул воздуха

Физика Какова концентрация молекул в воздухе при нормальных условиях?

Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.

О каком газе пойдет речь?

В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.

Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H₂O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.

Универсальный закон Клапейрона-Менделеева

Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:

P*V = n*R*T.

Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R — это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).

Концентрация молекул и ее вычисление

Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:

c_N = N/V.

Где N — общее число частиц в системе.

Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана k_B:

n = N/N_A;

k_B = R/N_A.

Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:

P*V = n*R*T =>

P*V = N/N_A*R*T = N*k_B*T =>

c_N = N/V = P/(k_B*T).

Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.

Поскольку количество частиц в системе велико, то концентрацией c_N пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию c_n. Она для идеального газа определяется так:

c_n = n/V = P/(R *T).

Пример задачи

Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P₀, где P₀ = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 ^oC (273,15 К).

Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:

c_n(O₂) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м³.

Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.

Чтобы понять, сколько молекул O₂ содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число N_A. Выполнив эту процедуру, получим огромное значение: N(O₂) = 5,64*10²¹ молекул.

При
рассмотрении закона распределения
Максвелла предполагалось, что молекулы
равномерно распределяются по всему
объему сосуда, что справедливо, если
объем сосуда небольшой.

Для
больших объемов равномерность
распределения молекул по объему
нарушается из-за действия силы тяжести,
вследствие чего плот­ность, а
следовательно, и число молекул в единице
объема будут неодинаковым.

Рассмотрим
молекулы газа, находящегося в поле
тяготения Земли.

Выясним
зависимость давления атмосферы от
высоты над поверхно­стью Земли.
Допустим, на поверхности Земли (h
= 0) давление атмосфе­ры P₀.
На высоте h
оно равно P.
При увеличении высоты на dh
давление уменьшится на dP:

dP
= — ρgdh
(9.49)

[ρ
— плотность воздуха на данной высоте,
ρ
= mn₀,
где m
— масса моле­кулы, n₀
— концентрация молекул].

Используя
соотношение P
= n₀kТ,
получаем

тогда

(9.50)

Полагая,
что на некоторой высоте h
Т = соnst,
g
= соnst,
разделяя пе­ременные, интегрируем
выражение (9.50):

,

Получаем

(9.51)
—
барометрическая
формула.

Барометрическая
формула показывает зависимость давления
газа от высоты над поверхностью Земли.

Если
учесть, что концентрация молекул воздуха
в атмосфере определяет дав­ление, то
формулу (9.51) можно записать в виде

(9.52)

Из
формулы (9.52) следует, что с понижением
температуры число частиц на высоте,
отличной от нуля, убывает и при Т = 0К
обращается в нуль, т. е. при 0К все молекулы
расположились бы на земной поверх­ности.

Так
как потенциальная энергия молекул на
различной высоте раз­лична и на высоте
h
определяется по формуле где Е_П
= mgh,
то [см.

(9.53)

— закон
Больцмана,
показывающий распределение участвующих
в теп­ловом движении молекул в
потенциальном поле сил, в частности в
поле силы тяжести.

Методика решения задач

В задачах
данного типа используют свойства
распределения Максвелла и Больцмана.

Пример
3.3. Определите
среднюю арифметическую скорость <υ˃
молекул идеального газа, плотность
которого при давлении 35 кПа составляет
0,3 кг/м³.

Дано:
Р=35кПа=35∙10³
Па; ρ=0,3
кг/м³.

Найти:
<υ˃.

Решение:
Согласно
основному уравнению молекулярно-кинетической
теории идеальных газов,

,
(1)

где
n
– концентрация молекул; m₀—
масса одной молекулы; <υ_кв˃.-
средняя квадратичная скорость молекул.

Учитывая,
что
,
а,
получаем

Так
как плотность газа

,

где
m
– масса газа; V
— его объём; N
— число молекул газа, уравнение (1) можно
записать в виде

или
.
Подставляя это выражение в формулу (2),
находим искомую среднюю арифметическую
скорость:

Ответ:
<υ˃=545
м/с.

Пример
3.5. Найти относительное
число газа, скорость которого отличается
не более чем на δη = 1% значения средней
квадратичной скорости.

Дано:
δη = 1%.

Найти:

Решение В распределении
Максвелла

подставим
значение

;
δυ = υ_квδη.

Относительное
число молекул будет

Ответ:

Пример
3.6. При какой температуре
газа число молекул со скоростями в
заданном интервале υ, υ + dυ будет
максимальной? Масса каждой молекулы m.

Решение

Для
нахождения искомой температуры необходимо
исследовать функцию распределения
Максвелла на экстремум
.

.

Пример
3.7. Вычислить наиболее
вероятную, среднюю и среднюю квадратичную
скорости молекул идеального газа, у
которого при нормальном атмосферном
давлении плотность ρ = 1кг/м³.

Решение

Умножив числитель и знаменатель
в подкоренных выражениях (3.4) на число
Авогадро N_а,
получим следующие формулы для скоростей:

.

Запишем уравнение Менделеева-Клапейрона,
введя в него плотность

ΡRT = MP

Определим отсюда величину
и, подставив её в выражения, определяющие
скорость молекул, получим:

Пример
3.4. Идеальный газ с
молярной массой M находится в однородном
поле тяжести, ускорение свободного
падения в котором g. Найти давление газа
как функцию высоты h, если при h = 0 давление
Р = Р₀,
а температура меняется с высотой как T
= T₀(1
— α·h), где α – положительная постоянная.

Решение

При
увеличении высоты на бесконечно малую
величину давление получает приращение
dP = — ρgdh, где ρ — плотность газа. Знак
минус появился, так как с увеличением
высоты давление уменьшилось.

Поскольку рассматривается идеальный
газ, плотность ρ может быть найдена из
уравнения Mенделеева-Клапейрона:

Подставим значение плотности
ρ и температуры Т, получим разделяя
переменные:

Интегрируя это выражение, находим
зависимость давления газа от высоты h:

Так
как при h = 0 Р = Р₀
получаем значение постоянной интегрирования
С = Р₀.
Окончательно функция Р( h ) имеет вид

Необходимо отметить, что, так
как давление является величиной
положительной, полученная формула
справедлива для высот
.

Пример.
Французский
физик Ж.Перрен, наблюдал под микроскопом
изменение концентрации взвешенных в
воде (ρ=1г/см³)
шариков гуммигута (ρ ₁=1,25г/см³)
с изменением высоты, экспериментально
определил постоянную Авогадро. Определите
это значение, если температура взвеси
Т=298К, радиус шариков =0,21 мкм, а при
расстоянии между двумя слоями Δh=30мкм
число шариков гуммигута в одном слое в
два раза больше, чем в другом.

Дано:
ρ=1г/см³=1000кг/м³;
ρ=1,25 г/см³=1250кг/м³;
Т=280 К; r=0,21мкм=0,21∙10^-6
м; Δh=30мкм=3∙10^-5
м;
.

Найти:
N_A.

Решение.
Барометрическую
формулу

,

Используя
уравнение состояния P=nkT,
можно преобразовать для высот h₁
и h₂
к виду

и


,

где
n₀,
n₁
и n₂—
соответственно концентрация молекул
на высоте h₀,
h₁
и h₂;
М – молярная масса; g-
ускорение свободного падения; R-
молярная газовая постоянная.

Тогда

.
(1)

Прологарифмировав
выражение (1), получим

(2)

Масса
частицы
;
m=ρV=ρπr³.
Подставив эти формулы в (2) и учитывая
поправку на закон Архимеда, получим

Откуда
искомое выражение для постоянной
Авогадро

Ответ:
N_A=6,02∙10²³моль^-1.

Пример.
Какова
температура Т азота, если средняя длина
свободного пробега <ℓ˃ молекул азота
при давлении Р=8кПа составляет 1мкм.
Эффективный диаметр молекул азота
d=0,38нм.
.

Дано:
<ℓ˃
=1мкм=1∙10^-6
м;
Р=8кПа=8∙10³
Па;
d=0,38нм=0,38∙10^-9м;

Найти:
Т.

Решение.
Согласно
уравнению состояния идеального газа

P=nkT,

где
n
– концентрация молекул; k
— постоянная Больцмана.

Средняя
длина свободного пробега молекул газа

,

откуда
.
Подставив эту формулу в выражение (1),
найдём искомую температуру азота

Ответ:
Т=372 К.

Пример.
При
температуре Т=280 К и некотором давлении
средняя длина <ℓ₁˃
свободного
пробега молекул равна 0,1 мкм. Определите
среднее число <z₂˃
столкновений
молекул в 1с, если давление в сосуде
уменьшить до 0,02 первоначального давления.
Температуру считать постоянной, а
эффективный диаметр молекулы кислорода
принять равным 0,36нм .

Дано:
Т=280 К; <ℓ₁˃
=0,1мкм=0,1∙10^-6
м;
М=32∙10^-3
кг/моль;

;
d=0,36нм=0,36∙10^-9м;

Найти:
<z₂˃.

Решение.
Среднее число <z₂˃
столкновений молекулы в 1с при конечном
давлении определяется отношением
средней скорости <υ˃.
молекулы к средней длине её свободного
пробега <ℓ₂˃.
при том же давлении:

,
(1)

где
средняя скорость молекул определяется
по формуле

(2)

где
R
– молярная газовая постоянная; М –
молярная масса вещества.

Из
формул
иP=nkT
следует, что средняя длина свободного
пробега молекул обратно пропорциональна
давлению:

,

откуда
.
Подставив это выражение в формулу (1) и
учитывая (2), получаем искомое среднее
число столкновений молекул в 1с:

Ответ:
<z₂˃
= 8,61∙107с^-1.

Пример.
Можно
ли считать вакуум 100мкПа высоким, если
он создан в колбе радиусом r=15
см, содержащей азот при 0ºС. Эффективный
диаметр молекулы азота d=0,38нм.
.

Дано:
P=100мкПа=10^-4Па;
r
=15см=0,15
м;
T=273
К;
d=0,38нм=0,38∙10^-9м.

Найти:

Решение.
Вакуум
можно считать высоким, если средняя
длина свободного пробега молекул газа
гораздо больше линейных размеров сосуда,
т.е. должно выполняться условие

˃˃2r

Средняя
длина свободного пробега молекул газа

(учли
P=nkT).

Вычисляя,
получаем
=58,8
м, т.е 58,8 м ˃˃0,3 м.

Ответ:
да, вакуум высокий.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Концентрация частиц – это величина, показывающая, сколько частиц вещества находится в каком-либо объеме. Она вычисляется по формуле: c = N/V, ее размерность 1/м^3. Часто возникает необходимость определить концентрацию молекул, причем исследуемое вещество может быть в любом агрегатном состоянии: твердом, жидком или газообразном.

Представьте, что любознательный царь Гиерон дал своему придворному математику еще одну корону, приказав: «Вот она-то точно из чистого золота. Определи, Архимед, какова концентрация молекул в ней». Гениального ученого такая задача поставила бы в тупик. Ну, а вы решите ее очень быстро. Предположим, корона весила бы ровно 1,93 килограмма, занимая при этом объем в 100 см^3.

Прежде всего найдите, сколько молей золота содержится в таком количестве вещества. С помощью таблицы Менделеева вы узнаете молекулярную массу золота: 197 а.е.м. (атомных единиц массы). А масса одного моля любого вещества (в граммах) численно равна его молекулярной массе. Следовательно, один моль золота весит 197 грамм. Разделив фактическую массу короны на молярную массу золота, вы получите: 1930/197 = 9,79. Или, округленно, 9,8 молей золота.

Умножьте количество молей на универсальное число Авогадро, показывающее, сколько элементарных частиц содержится в моле любого вещества. 9,8*6,022*10^23 = 5,9*10^24. Вот сколько молекул золота приблизительно содержится в короне.

Ну, а теперь найти концентрацию молекул проще простого. 100 кубических сантиметров – это 0,0001 м^3. Разделим: 5,9*10^24/0,0001 = 5,9*10^28. Концентрация молекул золота равна 5,9*10^28/м3.

Теперь предположим, что вам задана такая задача: при давлении Р, средняя квадратичная скорость молекул углекислого газа равна V. Требуется определить концентрацию его молекул. И здесь нет ничего сложного. Существует так называемое основное уравнение кинетической теории идеального газа: Р = V^2m0C/3, где C – концентрация молекул газа, а m0 – масса одной его молекулы. Следовательно, искомая концентрация С находится так: С = 3P/m0V^2.

Единственная неизвестная величина – m0. Ее можно узнать в справочнике по химии или физике. Можно также вычислить по формуле: m0 = M/Na, где М – молярная масса углекислого газа (44 грамм/моль), а Na – число Авогадро (6,022х1023). Подставив все величины в формулу, вычислите искомую концентрацию С.

Видоизмените условие задачи. Предположим, вам известны только температура Т и давление Р углекислого газа. Как по этим данным найти концентрацию его молекул? Давление и температура газа связаны формулой: P = CkT, где С – концентрация молекул газа, а К – постоянная Больцмана, равная 1,38*10^-23. То есть С = P/kT. Подставив в формулу известные величины, вы вычислите концентрацию С.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.