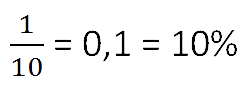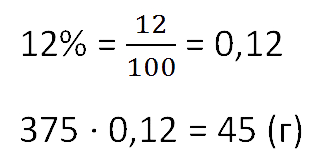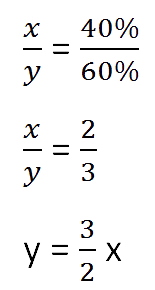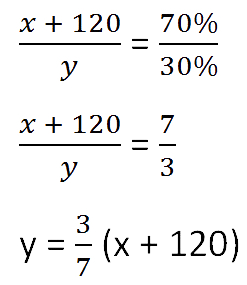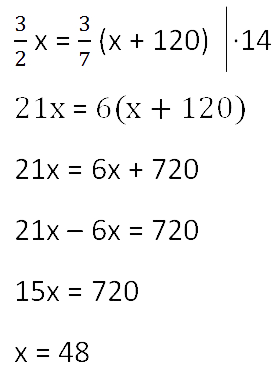Как найти концентрацию раствора 6 класс

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

• повторить понятия проценты, отношения;
• закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
• показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

• показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
• воспитание у учащихся интереса к предмету.

Развивающие

• развивать наблюдательность, логическое мышление учащихся;
• развивать жизненную смекалку и интуицию.

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.

План урока:

1. Мотивационный момент (1 минута).
2. Подготовка учащихся к сознательному усвоению нового материала (5 минут).
3. Изучение нового материала (12 минут).
4. Решение задач на отработку формул (3 мин).
5. Физминутка (1 минута).
6. Первичное закрепление нового материала (15минут).
7. Рефлексия (1 минута).
8. Подведение итогов. Домашнее задание (2 минуты).

Ход урока

I. Мотивационный момент.

Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.

II. Подготовка к сознательному усвоению нового материала.

(Слайд 2)

1. Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
2. Указать в виде процентов: 0,7; 0,04; 1,3.
3. Найти 15% от числа 60.
4. Найти число, 15% которого равны 30.
5. Из 25 семян взошло 24 семени. Найдите процент всхожести.
6. Итак, известные нам отношения: (Слайд 3)

Всхожесть = ; .

Значения данных отношений мы представляли в виде процентов.

III. Изучение нового материала.

Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?

В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].

Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].

Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)

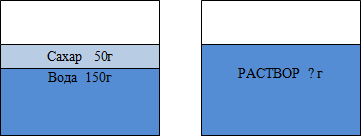
Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

50+150=200 (г) – масса общая. (Слайд 5)

Раствор тщательно перемешиваем.

Найдите процентное содержание сахара в растворе.

50 : 200=1: 4 = 0,25;

0,25=25%

25% – процентное содержание сахара в данном растворе.

Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)

Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).

Концентрация = , т.е. К=.

Как по этой формуле найти М_ч.в? М_общ?

М_ч.в. = М_общ · К

М_общ = Мч.в: К

(Слайд 7)

IV. Решение задач на отработку формул:

(Слайд

1. В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
2. 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
3. Какова масса раствора, в котором 150 г сахара составляют 25%.

Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)

Рис.1.

Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».

Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.

V. Физминутка.

(Слайд 11)

Следите глазами за движениями черепашек.

VI. Первичное закрепление нового материала.

Решим несколько задач на «концентрацию».

(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.

Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)

Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.

Решение:

1. Какова масса раствора в первой банке?
   480+120 = 600 (г)

2. Какова концентрация сахара в растворе первой банки?
   120:600 = 0,2; 0,2=20%

3. Какова масса раствора во второй банке?
   840+160 = 1000(г)

4. Какова концентрация сахара в растворе второй банки?
   160:1000 = 0,16; 0,16=16%

5. В какой банке вода слаще?
   20% > 16%

Ответ: в первой банке вода слаще.

Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)

Решение:

80% – это процентное содержание соли в 200г раствора (концентрация 0,8)

1. Сколько г соли в этом растворе?
   0,8 ·200=160(г)

20% – это содержание соли в 700 г раствора (концентрация соли 0,2)

1. Сколько г соли во втором растворе?
   0,2·700=140 (г)
2. Сколько г соли в полученном растворе?
   160+140=300 (г)

Ответ: 300 г.

Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)

Решение:

50% – процентное содержание соли в 200 г растворе (концентрация 0,5).

1. Сколько г соли в этом растворе?
   0,5·200=100 (г)
   Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25)

2. Какова масса второго раствора?
   150:0,25= 600 (г)
   Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора.

3. Какова масса соли в двух растворах?
   100+150=250 (г)

4. Какова масса нового раствора?
   200+600 =800 (г)

5. Какова концентрация соли в новом растворе?
   250:800=0,3125; 0,3125 = 31,25%

Ответ: 31,25%.

Задача для самостоятельного решения (дома).

Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]

Решение:

1. Сколько кг соли в морской воде?
   0,05·30=1,5 (кг)
   Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015.

2. Какова масса нового раствора (с добавлением пресной воды)?
   1,5: 0,015= 100 (кг)

3. Сколько пресной воды нужно добавить?
   100 – 30 = 70 (кг)

Ответ: 70 кг.

VII. Этап рефлексии.

(Слайд 18)

Ответ на листочке:

• Сегодня я узнал….
• У меня получилось…
• Было трудно….
• Было интересно….
• Теперь я умею…

VIII. Итог урока. Домашнее задание.

(Слайд 19)

№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.

Используемая литература:

1. Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. — 1456 с.: ил.
2. slovari. yandex.ru
3. urok.1sept.ru/articles/520040
4. Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
5. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. — 528 с.: ил.

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.

• 9%-я концентрация раствора соли — это 9 грамм соли в
  100 граммах раствора.

Разбор примера

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.

Ответ: 10% — концентрация раствора.

Разбор примера

Теперь решим обратную задачу.

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.

Сложная задача на растворы

В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет

100% − 40%= 60%

Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.

Этой величиной является масса воды в растворе «y».

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г — масса соли в новом растворе
• (100% − 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.

Ответ: 48 г — масса соли в первоначальном растворе.

---

Ваши комментарии

Оставить комментарий:

---

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Тема урока:
  «Задачи на концентрацию»

• 

  2 слайд

  Реши устно:
  1) Выразить десятичной дробью, а
  потом обыкновенной:
  25%, 10%, 50%, 75%, 125%.

  2) Указать в виде процентов: 0,7; 0,04; 1,3.

  3) Найти 15% от числа 60.

  4) Из 25 семян взошло 24 семени.
  Найдите процент всхожести.

• 

  3 слайд

  Проверим:
  1)

  2) 0,7=70%, 0,04=4%, 1,3=130%

  3)

  4)

• 

  4 слайд

  Концентрация…

  В большом энциклопедическом словаре
  «концентрация (от новолат. concentratio)
  сосредоточение, скапливание, собирание
  кого-либо, чего-либо в к.-л. месте».
  Концентрация в химии- величина,
  выражающая относительное количество
  данного компонента (независимой
  составной
  части) в физико-химической системе
  (смеси, растворе, сплаве).
  А в математике?

• 

  5 слайд

  Нальем в стакан 150 г воды и растворим в нем 50 г сахара. Какой станет концентрация раствора?
  1) 50+150=200(г) – масса нового раствора.
  2) 50 : 200=1: 4 = 0,25=25% — процентное содержание сахара в новом растворе.
  Число 0,25 называют концентрацией сахара в растворе.

• 

  6 слайд

  Определение: В математике концентрацию можно представить как отношение массы чистого вещества к массе всего раствора (сплава, смеси).

• 

  7 слайд

  Задачи, решаемые с помощью таблиц
  1. Задачи на движение:
  2. Задачи на нахождение площади и периметра прямоугольника:

  S= a⦁ b , P= (a + b) ⦁2 .
  S=v ⦁ t .

• 

  8 слайд

  Задачи, решаемые с помощью таблиц
  3. Задачи на использование формулы стоимости :
  4. Задачи на использование формулы объема параллелепипеда :
  C = a ⦁ n .
  V = a⦁b⦁c

• 

  9 слайд

  Задачи, решаемые с помощью таблиц
  5. Задачи на изменения.
  6. Задачи на движение по реке.

• 

  10 слайд

  Табличный метод решения задач на концентрацию:

• 

  11 слайд

  «Концентрацию» можно заменить на:
  «жирность»
  (масло, молоко)
  «крепость» (уксус)
  «соленость»
  (морская вода, маринад)

• 

  12 слайд

  «Концентрацию» можно заменить на:
  «влажность»
  (в воздухе)
  «проба»
  (в драгоценных металлах)

• 

  13 слайд

  Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще?
  1)
  2)

  — концентрация сахара в 1 банке.
  — концентрация сахара во 2 банке.
  Ответ: в первой банке вода слаще.

• 

  14 слайд

  Задача 2. Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
  1)
  -концентрация раствора.
  Ответ: 10% концентрация раствора.

• 

  15 слайд

  Задача 3. Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
  1)
  (г) – содержание соли в растворе.
  Ответ: 45 г содержание соли в растворе.

• 

  16 слайд

  Задача 4. В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
  1)
  2)

  содержание чистого вещества
  в растворе 1.
  — концентрация раствора 2.
  Ответ: 7% концентрация получившегося раствора.

• 

  17 слайд

  Задача 5. Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20% олова, второй, массой 200 г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?
  Ответ: 28% содержание олова.

• 

  18 слайд

  Задача 6. В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70%. Сколько грамм соли было первоначально в растворе?
  1)

  (г) — масса 1 раствора.
  2)
  — масса соли в растворе.
  (г)
  Ответ: 48 г масса соли в растворе.

• 

  19 слайд

  Задача 7. Виноград содержит 90% влаги, а изюм  — 5%. Сколько килограммов винограда требуется для получения 40 килограммов изюма?
  1)
  2)
  (кг) — масса сухого вещества.
  (кг) — масса винограда.
  Ответ: 380кг масса винограда.

• 

  20 слайд

  Сегодня я узнал….

  У меня получилось…

  Было трудно….

  Было интересно….

  Теперь я умею…

Краткое описание документа:

Открытый урок в 6 классе по теме «Задачи на смеси, растворы и сплавы»

Тип урока: урок объяснения материала

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

повторить понятия проценты, отношения;

закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;

показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;

воспитание у учащихся интереса к предмету.

Воспитывать интерес к предмету через межпредметные связи с химией, обращая внимание на аккуратность, дисциплинированность и самостоятельность.

Развивающие

развивать наблюдательность, логическое мышление учащихся;

развивать жизненную смекалку и интуицию.

развивать устную и письменную речь, внимание

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация, компьютер и проектор.

План урока:

• Мотивационный момент (1 минута).
• Подготовка учащихся к сознательному усвоению нового материала (5 минут).
• Изучение нового материала (12 минут).
• Решение задач на отработку формул (3 мин).
• Физминутка (1 минута).
• Первичное закрепление нового материала (15минут).
• Рефлексия (1 минута).
• Подведение итогов. Домашнее задание (2 минуты).

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 265 794 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Задачи на концентрацию

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Задачи на концентрацию являются основными задачами в школьном курсе химии, но различные способы решения таких задач можно рассматривать на уроках математики ещё с шестого класса, используя арифметический способ и понятие процента и десятичной дроби. Затем продолжить в седьмом классе изучив понятие пропорции, а так же умение решать задачи алгебраическим способом, то есть уравнением. И, наконец, в восьмом классе рассмотреть возможность решения таких задач с помощью систем уравнений.

При подготовке ГИА необходимо вспомнить и систематизировать типы и способы решения таких задач.

Арифметический способ

При изучении темы «Проценты» в 6 классе решение задач на концентрацию считаются задачами повышенной сложности и могут быть предложены особо подготовленным учащимся.

Задача 1. Имеется 735 г шестнадцатипроцентного раствора йода в спирте. Нужно получить десятипроцентный раствор йода. Сколько граммов спирта нужно долить для этого к уже имеющемуся раствору?

Решение:

1) Найдем, сколько чистого йода содержится в растворе.

735 · 0,16 = 117,6 (г).

2) В новом растворе йода останется такое же количество, но он будет составлять уже 10 % раствора.

Если 117,6 г – это 10 %, то весь раствор имеет массу 117,6 · 10 = 1176 (г).

3) Найдем, сколько спирта нужно долить для получения нового раствора.

1176 – 735 = 441 (г).

О т в е т: 441 г.

Алгоритм:

Найти массу чистого вещества в растворе. Эта масса будет сохраняться в новом растворе.

Найти массу нового раствора в соответствии с процентным содержанием в нем вещества.

Найти разность масс нового и старого растворов. [3]

Решение с помощью пропорции

Познакомившись с понятием пропорции в 7 классе, подобные задачи можно решать используя это понятие.

Задача 2. К 200 г 30 %-ного раствора соли долили 50 г воды. Какова концентрация полученного раствора?

Р е ш е н и е.

Составим соответствующую пропорцию, приняв за х массу соли в растворе:

200 г – 100 %

х г – 30 % , тогда х = = 60 г соли.

Масса нового раствора 200 + 50 = 250 г, но масса соли в нём не изменилась, т. е. получим

250 г – 100 %

60 г – х % , тогда х = = 24 % концентрация полученного раствора.

О т в е т: получили 24 %-ный раствор.

Задача 3. Смешали 12 л 15 %-ного раствора соляной кислоты и 10 л 10 %-ного раствора. Каково процентное содержание кислоты в полученном растворе? Ответ округлить до 0,1 %.

Р е ш е н и е

С помощью пропорций найдём массу кислоты в каждом растворе:

12 л – 100 %

х л – 15 %, х = = 1,8 л кислоты в первом растворе и

10 л – 100 %

х л – 10 %, х = = 1 л кислоты во втором растворе, всего 2,8 литра.

Так как масса кислоты не меняется, а общая масса растворов 12 + 10 = 22 л, то получим

22 л – 100 %

2,8л – х %, х = ≈ 12,7 %.

О т в е т: 12,7 % кислоты.[4]

Алгебраический способ

Задача 4. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 %-ный раствор?

Начнём решение этой задачи не с составления уравнения, а с вопросов, которые помогут уяснить условие и осознанно подойти к ее решению, используем так же при этом понятие пропорции.

Вопросы:

1) Сколько граммов соли содержится в имеющемся растворе?

(50 · 0,08 = 4 г.)

2) Если к имеющемуся раствору добавить воды, изменится ли массовая составляющая соли? (Нет.)

3) При добавлении воды изменится ли процентное содержание соли в растворе? (Да.)

4) Если к имеющемуся раствору добавить х г воды, какова станет масса всего раствора? (50 + х). Сколько граммов соли в нем будет? (4 г.)

5) Каково процентное содержание соли в новом растворе? (5 %.)

6) Какую пропорцию, согласно полученным результатам, можно составить?

4 г соли – 5 %

(50 + х) г раствора – 100 %.

Имеем уравнение:

5 (50 + х) = 400, откуда х = 30.

О т в е т: 30 г.

Алгоритм.

Поскольку при добавлении к раствору какого-либо вещества масса другого вещества не изменяется, а меняется его процентное содержание, то сначала необходимо найти массу неизменяющегося вещества.

Затем за х обозначить массу добавляемого вещества и составить пропорцию, в которой масса неизменного вещества будет составлять новое количество процентов, а масса всего раствора 100 %. [2]

Решим данные задачи по составленному выше алгоритму.

Задача 5. Сколько граммов воды нужно выпарить из 80 г 6 %-ного раствора соли, чтобы получить раствор, содержащий 10 % соли?

Решение:

Масса соли в имеющемся растворе равна 80 · 0,06 = 4,8 г. В новом растворе соль будет составлять 10 %.

Пусть х г воды нужно выпарить, тогда масса нового раствора будет равна (80 – х) г.

Составим пропорцию:

4,8 г соли – 10 %;

(80 – х) г раствора – 100 %.

Получаем уравнение:

10 (80 – х) = 4,8 · 100, откуда х = 32.

Ответ: 32 г.

Задача 6. Сколько граммов 75%-ного раствора кислоты надо добавить к 30 г 15%-ного раствора этой же кислоты, чтобы получить 50%-ный раствор?

х г — количество 75%-ного раствора кислоты, которое надо добавить;

(30 + х) г — масса получившегося 50%-ного раствора кис­лоты;

0,75х г — количество кислоты в х г 75%-ного раствора;

0,15 ∙ 30 г — количество кислоты в 30 г 15%-ного раствора;

0,5(30 + х) г — количество кислоты в 50%-ном растворе. Имеем уравнение:

кол-во кислоты кол-во кислоты кол-во кислоты

в 75%-ном + в 15%-ном = в 50%-ном

растворе растворе растворе

0,75х + 0,15 ∙ 30 = 0,5(30 + х)

0,75х + 0,15 ∙ 30 = 0,5(30 + х), откуда х = 46 г.

Ответ: 46 грамм.[1]

Решение задач с помощью систем уравнений

Задачи такого типа последние годы встречаются на Основном Государственном Экзамене и Едином Государственном Экзамене.

Задача 7. В колбу налили некоторое количество 60% -ного раствора со­ли и некоторое количество 80%-ного раствора этой же соли. Получили 35 мл раствора, содержащего 72% соли. Сколько миллилитров каждого раствора налили в колбу? Решим зада­чу, используя следующий план:

Обозначим буквами количество 60%-ного и 80%-ного раст­воров соли, налитых в колбу.

Запишем уравнение, связывающее эти две величины и об­щее количество раствора.

Определим количество соли в получившемся растворе.

Запишем уравнение, связывающее количество соли в 60%-ном, 80%-ном и получившемся растворах.

Составим систему и решим ее.

1) Пусть взяли х мл 60 %-ного раствора соли и у мл 80 %-ного раствора.

2) x + у = 35.

3) 0,6x + 0,8у (количество соли в получившемся растворе).

4) 0,6x + 0,8у = 35 ∙ 0,72.

0,6x + 0,8у = 25,2.

5)

Решив эту систему, получим, что х = 14 и у = 21.

Ответ: 14 мл 60 %-ного раствора и 21 мл 80 %-ного раствора.

Рассмотрим арифметический способ, который использовался в старину.

1) Найдем разность между процентным содержанием соли в каждом из имеющихся растворов и полученном растворе:

72 % – 60 % = 12 %;

80 % – 72 % = 8 %.

2) Эти результаты показывают, что 60 %-ного раствора нужно взять 8 частей, а 80 %-ного – 12 частей, то есть растворы должны быть взяты в отношении 2 : 3.

Поскольку в результате получим 35 мл раствора, то 60 %-ного взяли 14 мл, а 80 %-ного – 21 мл. [5]

Задача 8. Сразу после сбора урожая процентное содержание воды в бананах составляет 75%. После их перевозки процентное содержание воды в них становится равным 70%. Сколько килограммов бананов надо приобрести, чтобы после перевозки осталось 2500 кг бананов? [6]

Решение. Определим содержание так называемого «сухого вещества»: после сбора урожая его содержится 25%, после перевозки – 30%. Его масса после перевозки составит 2500 : 100 · 30 = 750 кг, но т. к. она остаётся неизменной и после сбора урожая это 25%, то нужно собрать 3000 кг бананов.

О т в е т: 3000 кг.

Задача 9. Смешав 25-процентныйи и 95-процентный растворы кислоты добавив 20 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси? [7]

Заключение

Задачи, которые мы решили,— это так называемая задача на концентрацию. Концентрацией раствора называют отношение массы содержащегося в нем сухого вещества к массе раствора, выражен­ное в процентах. С процентами приходится иметь дело и при реше­нии многих других задач, например задач на вычисление прибыли с банковских вкладов, дохода от инвестиций, на расчет объемов вы­полненных работ. Все такие задачи нетрудно решить, если вы уме­ете выражать проценты обыкновенной или десятичной дробью и ре­шать главную задачу на проценты — находить процент от заданной величины. Иногда удобно решать их или с помощью пропорции или системой уравнений. И тот и другой способы широко применяются при решении химических задач.

Литература

1. Дорофеев Г. В., Суворова С. Б. и др. Алгебра: учебник для 8 класса общеобразовательных учреждений. — М.: Просвещение, 2010. — 288 с.

2. Дюмина Т. Ю. Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. I полугодие.— Волгоград: Учитель, 2008. —205 с.

3. Дюмина Т. Ю. Математика. 6 класс: поурочные планы по учебнику Г. В. Дорофеева, С. Б. Суворовой, И. Ф. Шарыгина и др. Часть 1. — Волгоград: Учитель, 2006. — 235 с.

4. Калинина М. Ф. Алгебра. 7 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. — Волгоград: Учитель, 2008. — 223 с.

5. Дюмина Т. Ю. Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. II полугодие.— Волгоград: Учитель, 2009. —263 с.

6. Под редакцией Лысенко Ф.Ф. и Калабухова С.Ю. Математика 9 класс. Подготовка к ОГЭ-2016. 40 тренировочных вариантов. – Ростов-на-Дону: Легион, 2015. – 400 с.

7. Под ред. Ященко И.В. ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов. – М.: Издательство «Национальное образование», 2016. – 256 с.

Просмотров работы: 17501

Задача на растворы

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.

Запомните!

Концентрация раствора — это часть, которую составляет масса растворённого вещества от массы всего раствора.

• 9% -я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.

Задача № 322 (2) из Петерсона 6 класс (2010 г.)

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.

Ответ: 10% — концентрация раствора.

Задача № 353(2) из Петерсона 6 класс (2010 г.)

Теперь решим обратную задачу.

Сколько соли получится при выпаривании 375 граммов 12% -го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.

Сложная задача на растворы

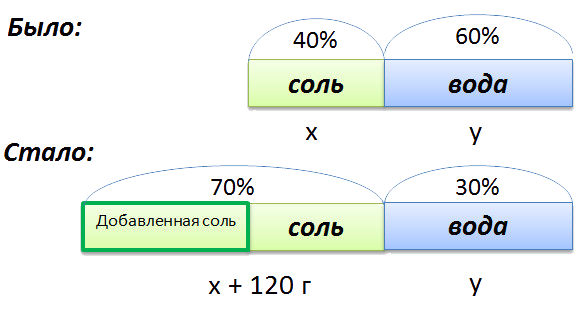
В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70 . Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за « x » первоначальную массу соли в растворе, а за « y » массу воды в растворе. Так как концентрация соли в исходном растворе 40% , то соответственно вода составляет

Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных (« x » или « y ») остаётся неизменной после добавления соли.

Этой величиной является масса воды в растворе « y ».

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г — масса соли в новом растворе
• (100% − 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.

Учитель математики . Здравствуйте, ребята. Сегодня на уроке математики мы познакомимся, и будем решать задачи, с которыми вы встретитесь и на уроках химии в старших классах. Помогать мне будет учитель химии нашей школы Абашеева Татьяна Васильевна.

Учитель химии . Ребята, в повседневной жизни мы встречаемся очень часто с растворами. Где? Кто может привести примеры растворов?

Дети перечисляют различные растворы.

Из чего состоят растворы?

Из растворителя и растворенного вещества.

На доске появляется запись: раствор = растворитель + растворенное вещество .

Роль растворителя могут выполнять разные жидкие вещества. Как вы думаете какие?

(Ученики называют бензин, керосин, спирт, воду).

В курсе химии вы встретитесь с различными растворами, в том числе и с «волшебными». Один такой волшебный раствор я хочу вам показать.

Демонстрационный опыт №1 .

В двух химических стаканах находится бесцветная жидкость (учитель в первый стакан налил раствор щелочи NaOH, а во второй фенолфталеин).

Учитель химии . Как вы думаете, каким будет цвет раствора, если мы смешаем эти две бесцветные жидкости?

Дети говорят, не задумываясь, что раствор останется бесцветным. И когда после смешивания он приобрел малиновую окраску, удивлению не было предела.

Учитель химии . Добавим в полученный раствор еще одну бесцветную жидкость (в стакане находится раствор серной кислоты). Какой станет окраска?

Теперь дети, учитывая предыдущий опыт, с ответом не торопятся. И предлагаются разные варианты ответов.

Раствор обесцветился. Этот демонстрационный опыт создал определенный эмоциональный настрой и активизировал мышление учащихся.

Учитель химии . Почему изменился цвет раствора, мы сможем сказать при изучении химии.
А сейчас давайте посмотрим на следующий опыт.

Демонстрационный опыт №2

Предлагаются к рассмотрению два химических стакана, в которых находится одинаковое количество жидкости. В первый стакан добавляем 5г вещества, а во второй 15г вещества. Получается разная окраска.

Учитель математики . Вы все видели, что в стаканах первоначально находилось одинаковое количество жидкости. В них добавили одно и тоже вещество . Почему же получилась разная окраска?

Учащиеся говорят, что добавили разное количество вещества, поэтому получилась разная окраска.

Учитель математики . Для того чтобы грамотно выразить различия этих и других растворов введем новое понятие «процентная концентрация».

Процентной концентрацией раствора называют процентное содержание растворенного вещества в единице массы раствора.

Масса раствора складывается из массы вещества и массы растворителя.

Давайте вернемся ко второму опыту. В первом стакане было 100 г жидкости, добавили 15г вещества. Какой стала масса раствора? 115г. А %-ная концентрация? ∙100%=13 %. А во втором стакане было 100 г жидкости, добавили 25г вещества. Какой стала масса раствора? 125г. А %-ная концентрация? ∙100%=20%

Ребята, зачем нам нужно понятие «%-ная концентрация»? Где мы с этим сталкиваемся

в повседневной жизни? Медицина, бытовая химия и т.д. Давайте устно решим с вами следующую задачу.

Для консервирования огурцов приготовили рассол: на 2л воды взяли 100г соли, а для консервирования томатов — рассол из 100г соли на 3л воды. Какой рассол получился более

В результате обсуждения ученики делают вывод, что чем больше растворителя при равном количестве растворенного вещества, тем меньше концентрация. Здесь проводим аналогию с правилом сравнения двух дробей с одинаковыми числителями.

Учитель обращает внимание на то, что только для воды 1л=1кг. Для других жидких веществ это равенство не выполняется. Необходимая запись делается на доске.

Учитель химии . Ребята, %-ную концентрацию Вы научились считать. Теперь я хочу усложнить вам задачу.

Демонстрационный опыт №3

Предлагаю к рассмотрению два химических стакана. В первом стакане 100г раствора и растворено 10 г вещества. Чему равна процентная концентрация этого раствора?

( Один ученик выполняет вычисления на доске. Получает ответ 10%.)

Во втором стакане 50г раствора и растворено 5 г вещества. Чему равна процентная концентрация этого раствора?

( Другой ученик выполняет вычисления на доске. Получает ответ 10%.)

Мы убедились, что процентная концентрация одинаковая. Давайте смешаем эти два раствора. Какая получилась концентрация получившегося раствора?

Учащиеся работают самостоятельно. Предлагаются разные варианты ответов. Идет обсуждение и записывается правильный ответ: %-ная концентрация= ∙100%=10%.

Учитель математики . Давайте подведем промежуточный итог. Ответьте мне на вопросы:

Из чего состоит раствор? ( Из растворителя и растворенного вещества).

Как найти массу раствора? ( Масса раствора складывается из массы вещества и массы растворителя) .

Как посчитать %-ную концентрацию раствора?

Хорошо. А теперь давайте рассмотрим еще несколько задач.

№1. На полке 280 книг. Из них 70% по математике. Сколько книг по математике на полке?

Дети решают самостоятельно в тетрадях, потом один ученик записывает решение на доске.

Сравни с предыдущей и реши такую задачу.

№2. Сколько граммов сахара содержится в 250 граммах 12%-ного раствора сахара?

Чем похожи эти задачи?

В результате обсуждения приходят к выводу, что обе задачи на нахождении части от целого.

№3. В шкафу 64 книги на английском языке, что составляет 40% от всех книг. Сколько всего книг в шкафу?

Дети решают самостоятельно в тетрадях.

Сравни с предыдущей и реши такую задачу.

№4. Найди массу 10%-ного раствора соли, если известно, что соли в растворе 0,2 кг.

Чем похожи эти задачи? Приходим к выводу, что эти две задачи на нахождение целого по его части.

Учитель химии . А я предлагаю вам такую задачу.

№5. В лаборатории имеется 2л 18%-ного раствора щелочи. В раствор добавили 2л воды. Каким стало процентное содержание щелочи в новом растворе?

Идет обсуждение решения.

Сколько щелочи было первоначально в растворе? 2∙0,18=0,36(л)

Какой стала масса раствора после добавления воды? 2+2=4(л)

Найдите %-ную концентрацию раствора. ∙100%=9%

Учитель химии . Сегодня на уроке у вас было первое знакомство с наукой химией. Мы начали урок с «волшебства», давайте и закончим его «волшебством».

Демонстрационный опыт №4

Предлагается опыт, напоминающий извержение вулкана.( В результате сжигания бихромата аммония выделяется азот, происходит изменение оранжевого цвета на серо-зеленый.)

Каталог статей

• 9%-я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.

Задача из Петерсона 6 класс (2010 г.) № 322 (2)

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.

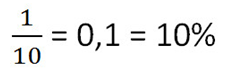
Ответ: 10% — концентрация раствора.

Задача из Петерсона 6 класс (2010 г.)
Теперь решим обратную задачу.№ 353(2)

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

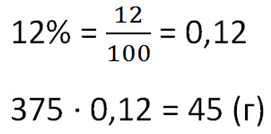
Ответ: 45 г соли.

Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за x первоначальную массу соли в растворе, а за y массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет

100% — 40%= 60%
Изобразим графически условия задачи.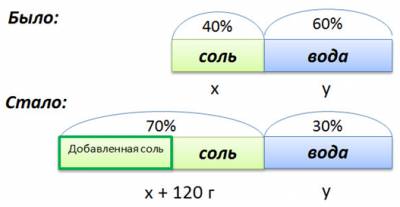

Составим пропорцию, связывающую эти величины до добавления соли.

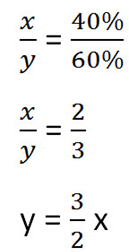
Для решения задачи нам надо определить какая из неизвестных (x или y) остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе (y).
Выразим её, учитывая изменения в растворе после добавления соли.
• (x + 120) г — масса соли в новом растворе
• 100% — 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.

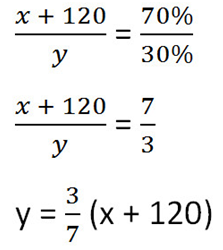
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.

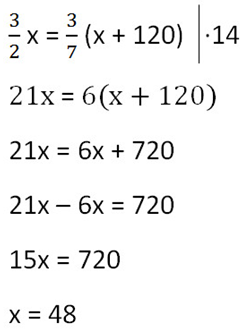
Ответ: 48 г — масса соли в первоначальном растворе.