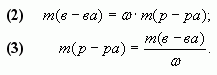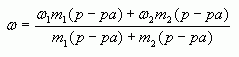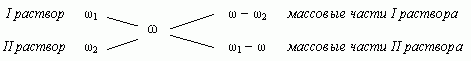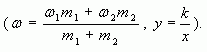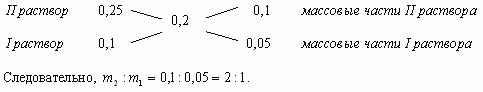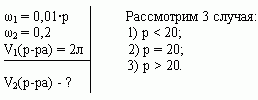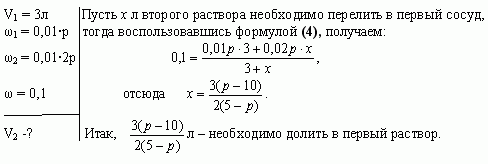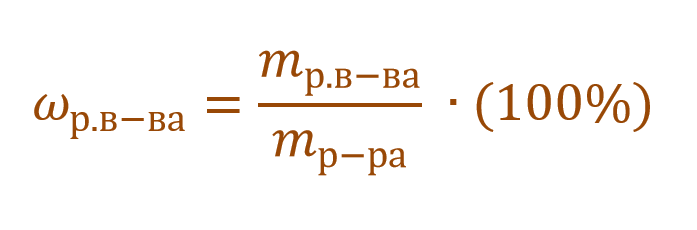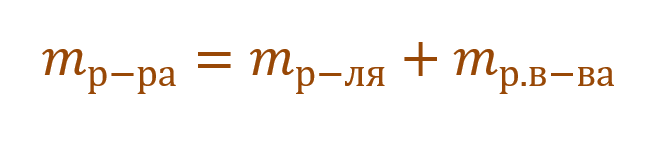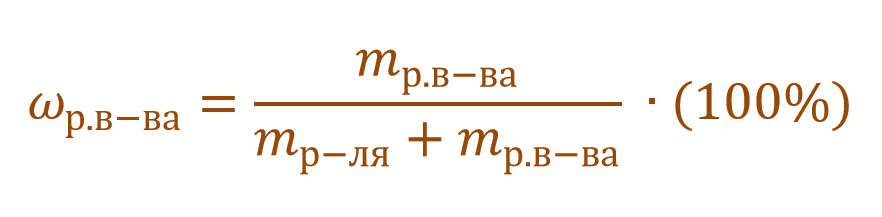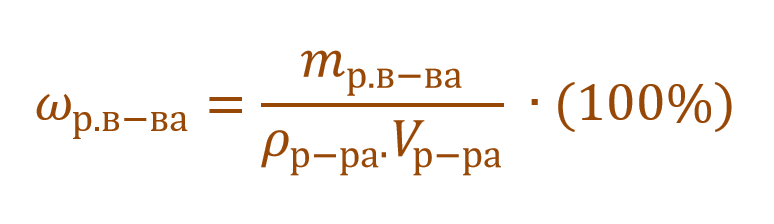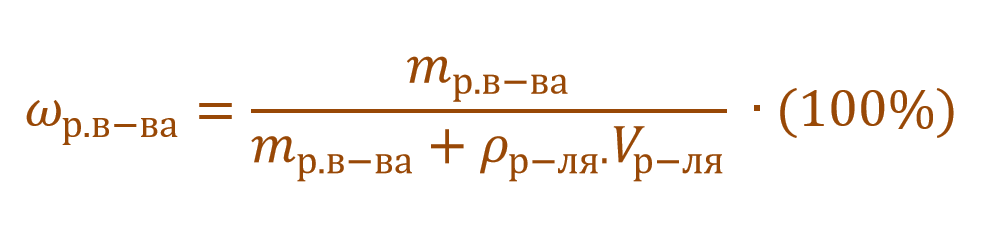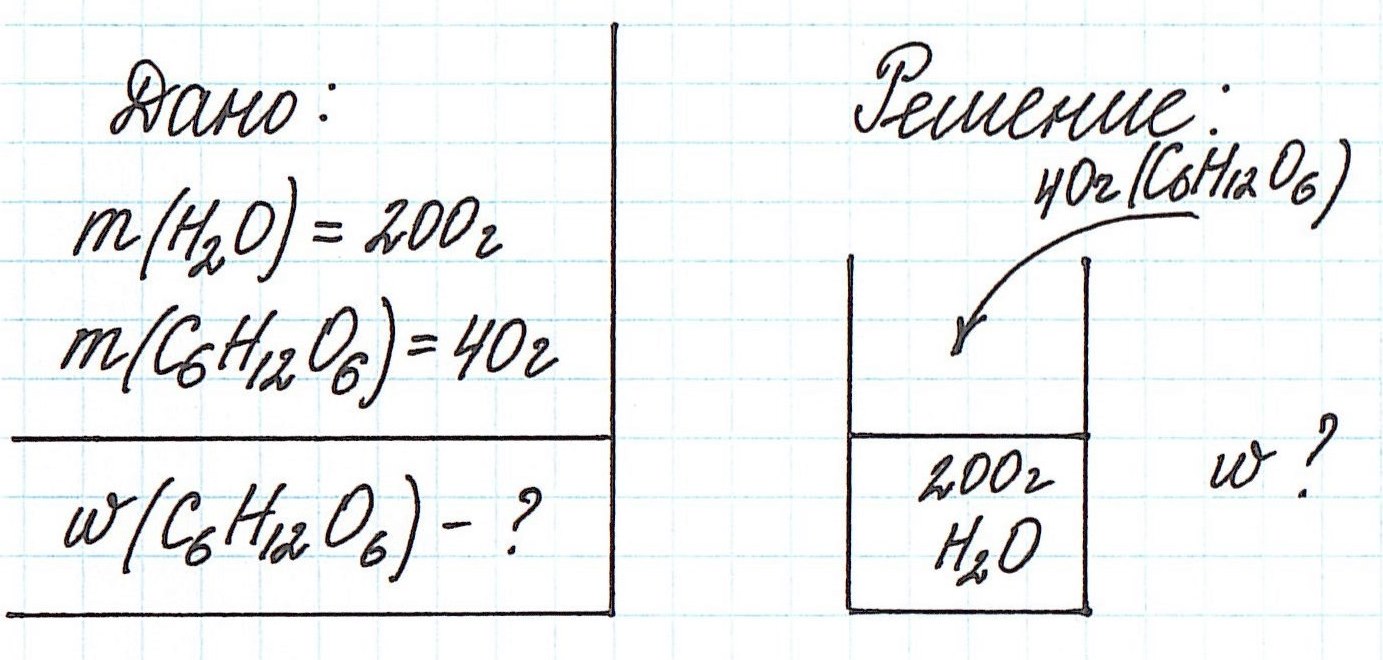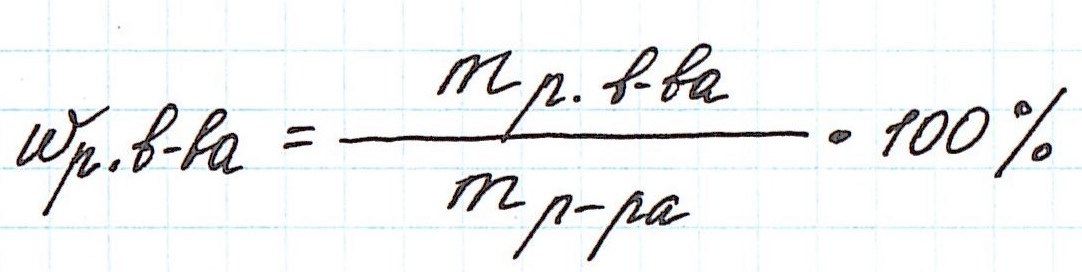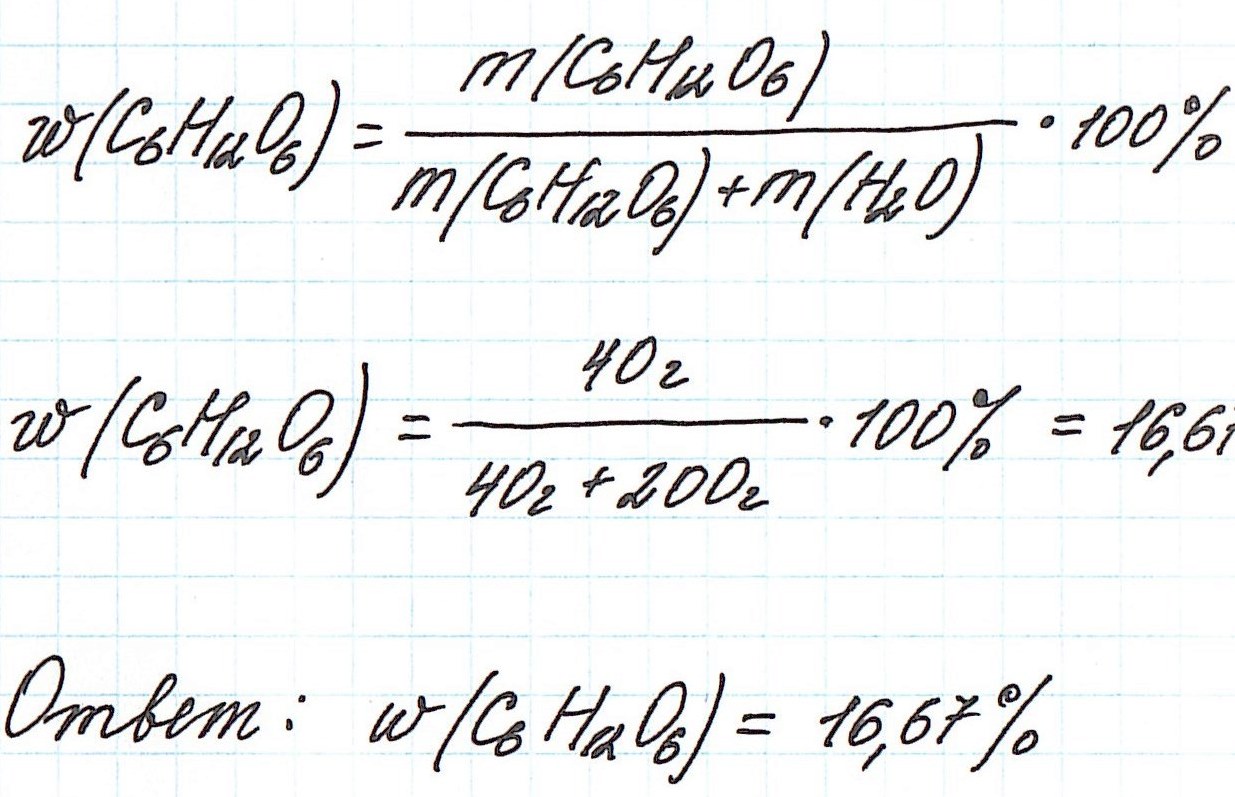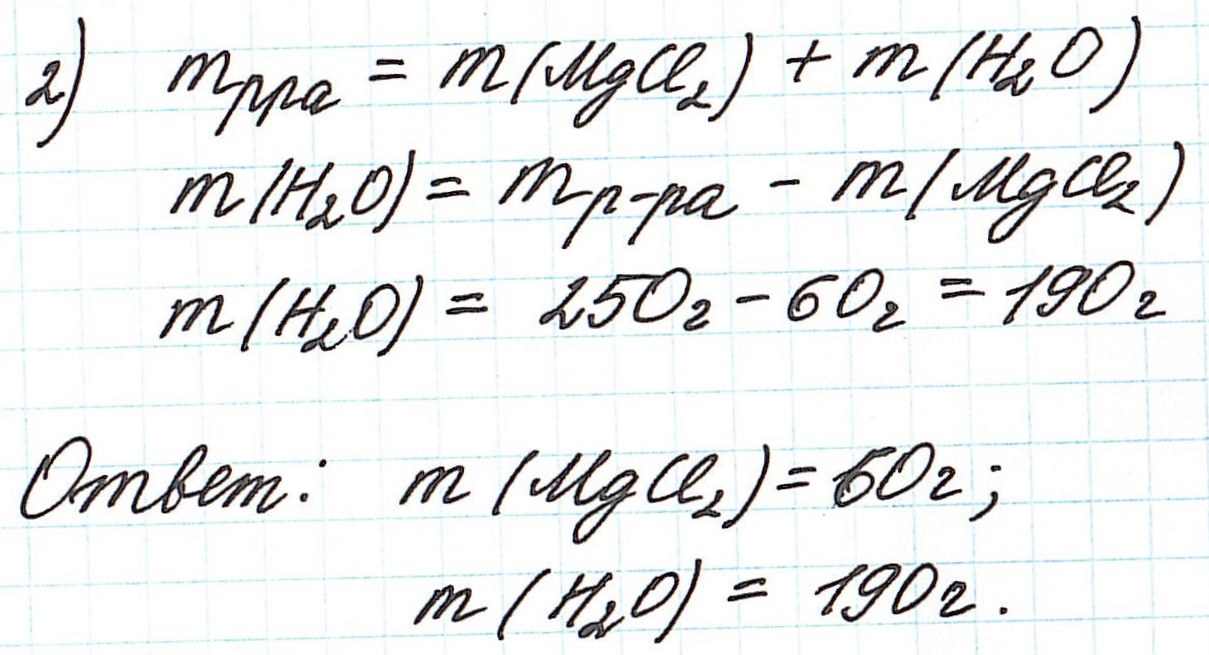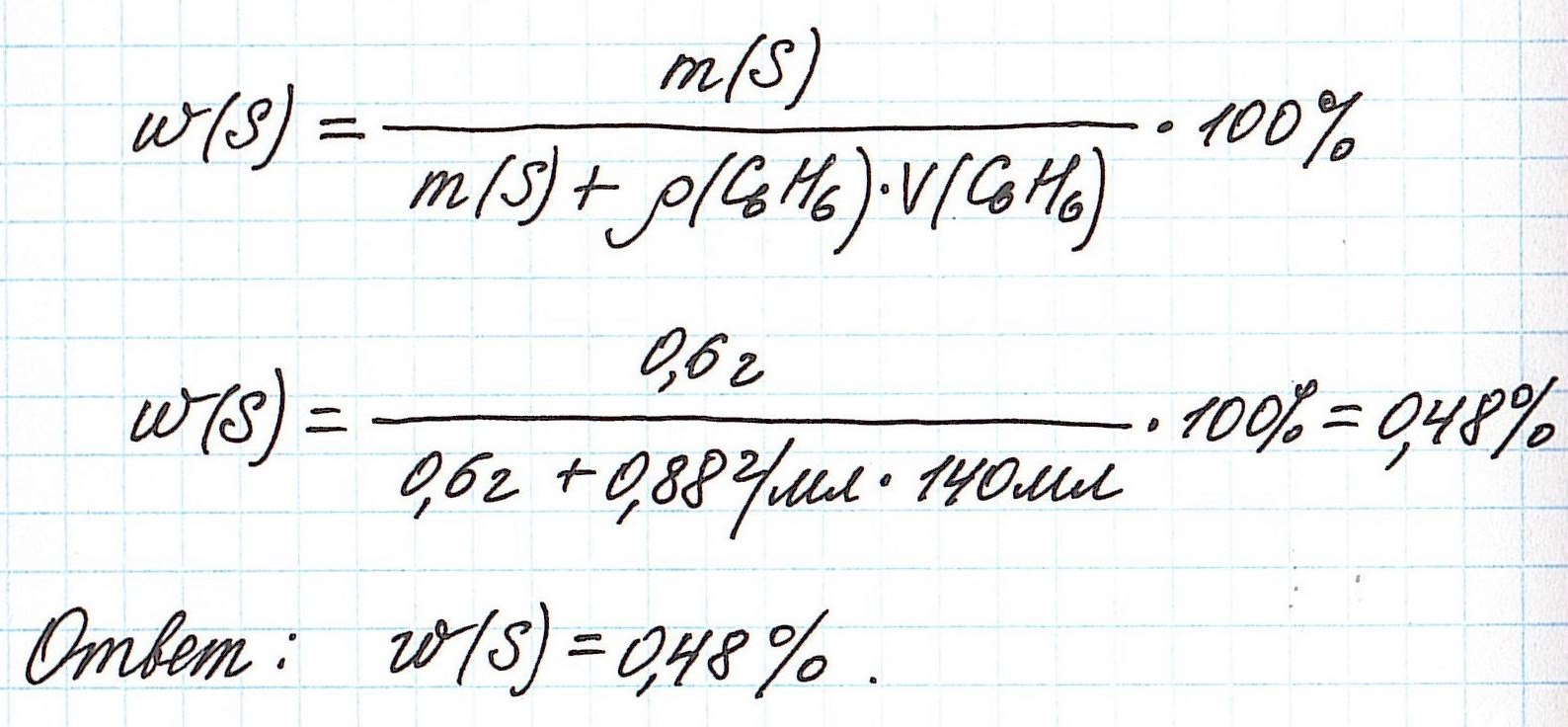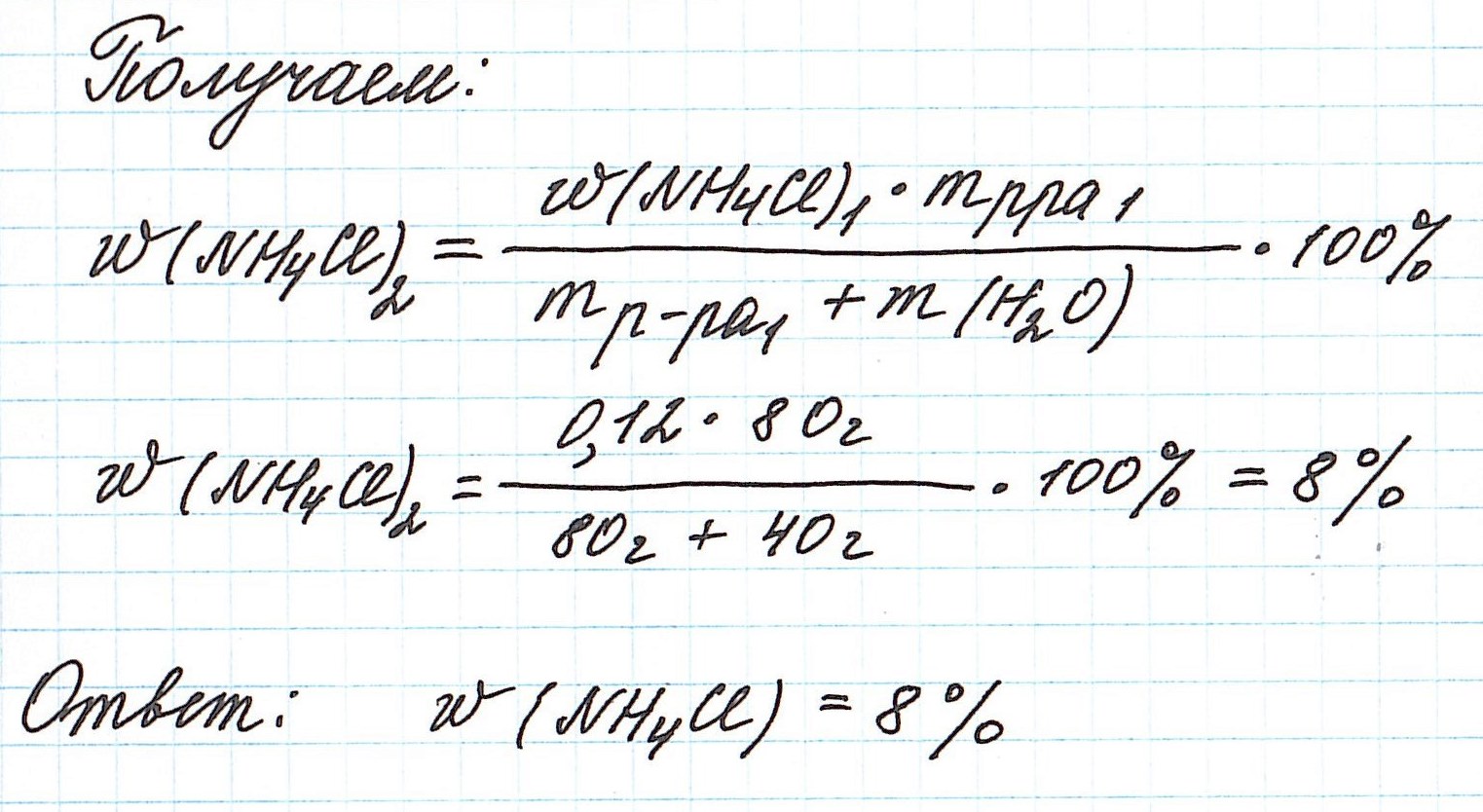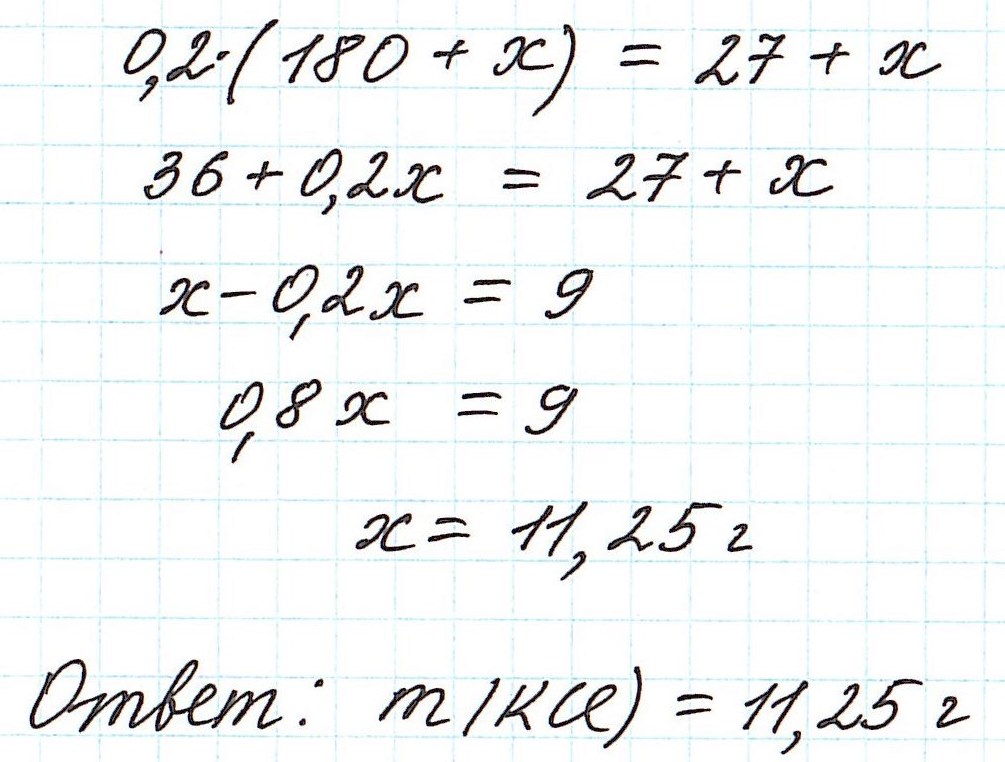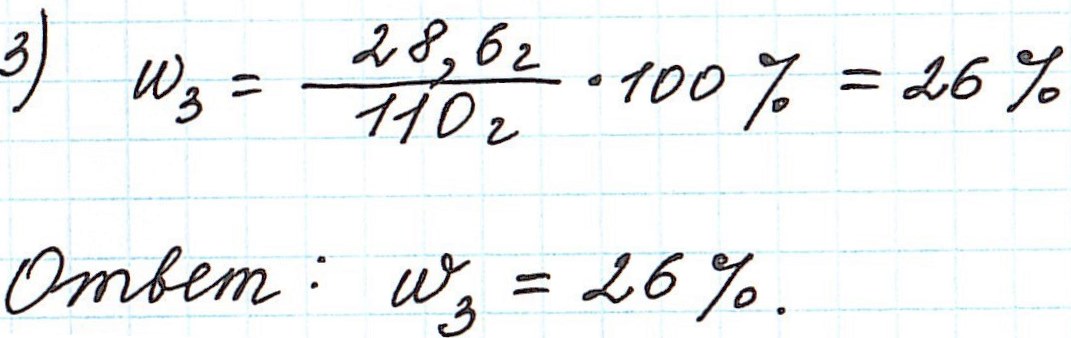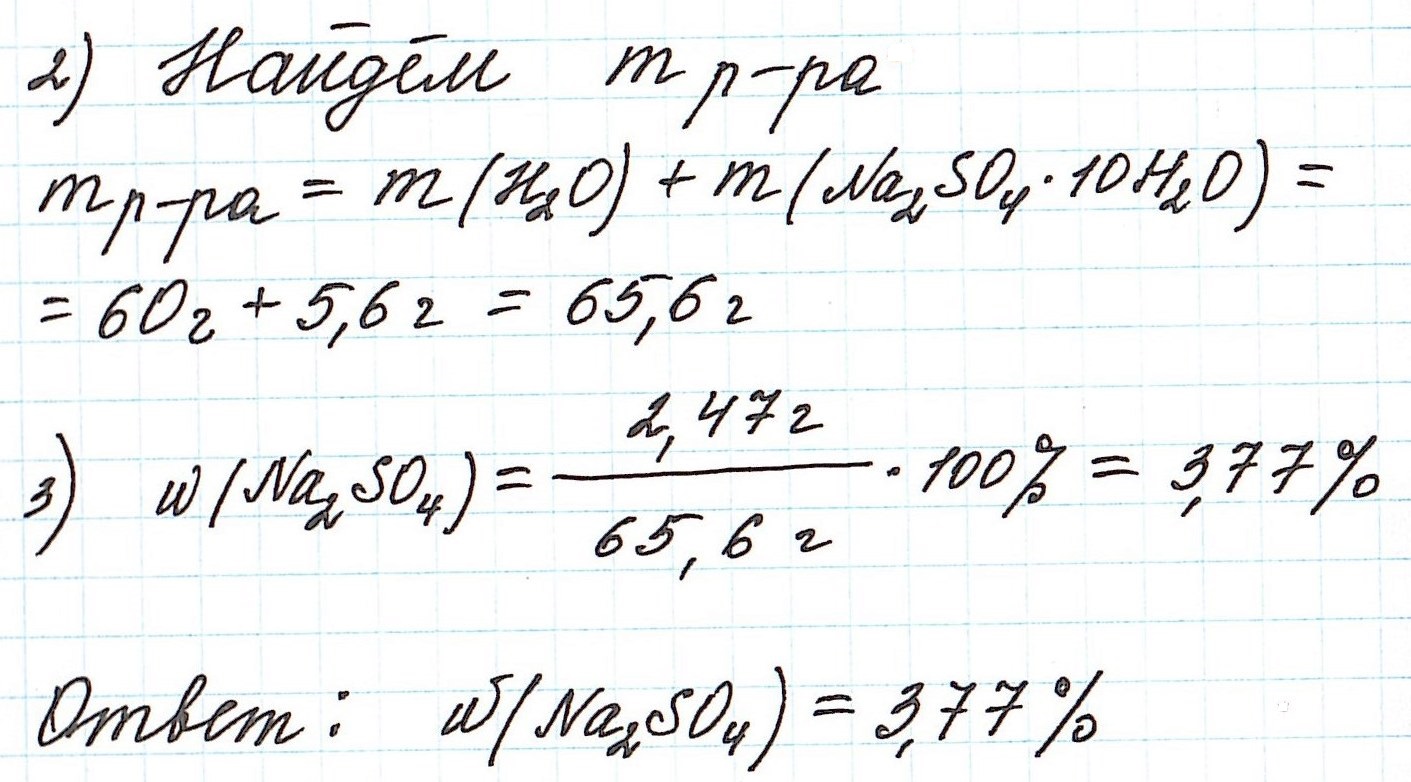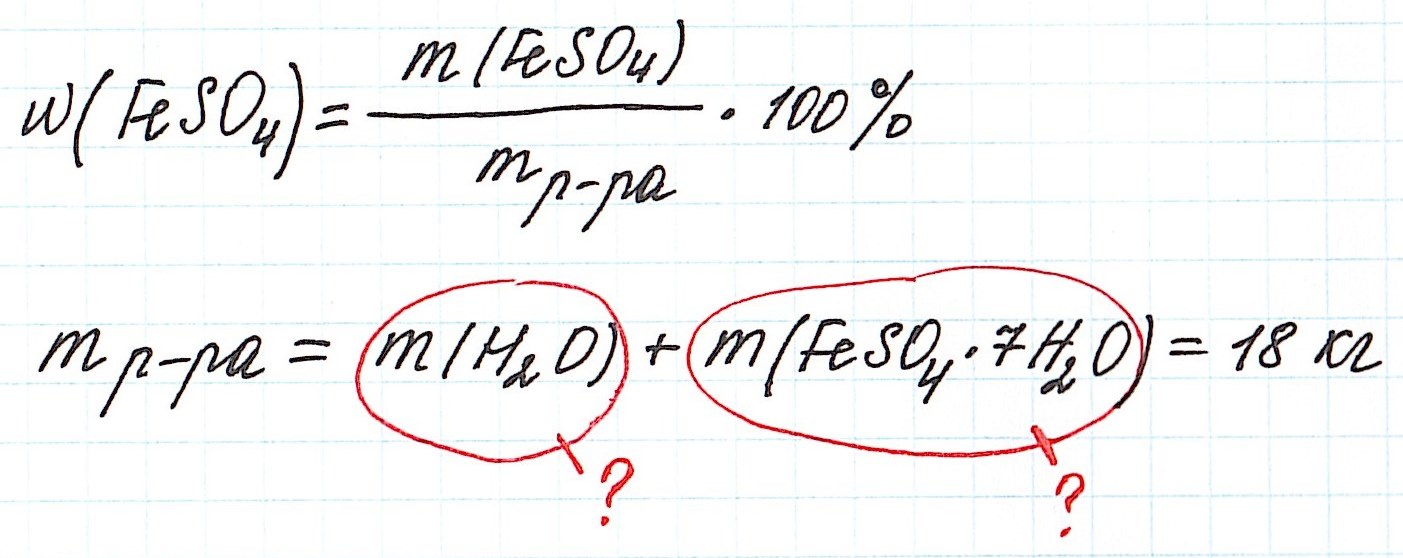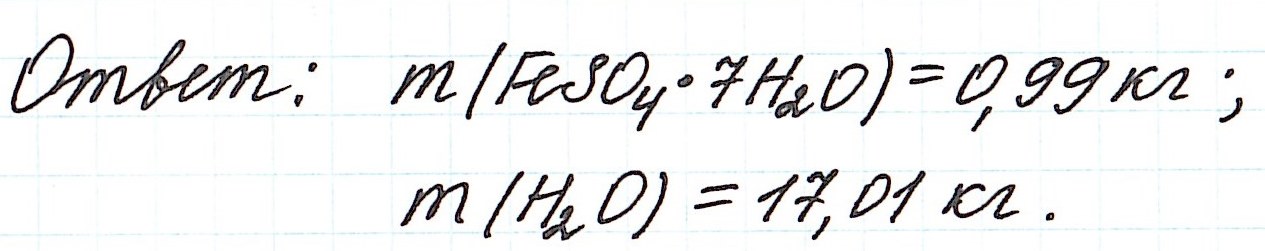“Только из союза двоих, работающих
вместе и при помощи друг друга, рождаются великие
вещи.”
Антуан Де Сент-Экзюпери
Математика многообразна и многогранна.
Существует ряд ситуаций в образовательном
процессе, когда при изучении какой-либо темы по
физике, химии, биологии и т.д. затрагиваются
понятия математики, например, существуют задачи,
которые решают как на уроках математики, так и на
уроках химии. Способы решения задач представляют
и учителя химии, и математики, но есть проблема:
математики знают математику, а химики — химию. И
не всегда способы совпадают.
В данной статье приводятся рекомендации по
решению химических задач на смешение растворов
разными способами: с помощью расчетной формулы,
“Правила смешения”, “Правила креста”,
графического метода, алгебраического метода.
Приведены примеры решения задач.
1. Основные химические понятия
Приведем некоторые указания к решению задач на
растворы.
Основными компонентами этого типа задач
являются:
а) массовая доля растворенного вещества в
растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются
однородными;
б) смешивание различных растворов происходит
мгновенно;
в) объем смеси равен сумме объемов смешиваемых
растворов;
г) объемы растворов и массы сплавов не могут
быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в
растворе — это отношение массы этого вещества к
массе раствора.
где — массовая
доля растворенного вещества в растворе;
— масса
растворенного вещества в растворе;
— масса
раствора.
Следствия формулы (1):
Введем обозначения:
— массовая доля
растворенного вещества в первом растворе;
—
массовая доля растворенного вещества во втором
растворе;
—
массовая доля растворенного вещества в новом
растворе, полученном при смешивании первого и
второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) — массы
растворенных веществ в соответствующих
растворах;
m1(р-ра), m2(р-ра), m(р-ра) — массы
соответствующих растворов.
Основными методами решения задач на смешивание
растворов являются: с помощью расчетной формулы,
“Правило смешения”, “Правило креста”,
графический метод, алгебраический метод.
Приведем описание указанных методов.
1.1. С помощью расчетной формулы
В наших обозначениях, получим формулу для
вычисления массовой доли вещества (?) в смеси.
1. Масса полученного при смешивании раствора
равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в
первом и втором растворах:
m1(в-ва)= •m1(р-ра), m2(в-ва)=
•m2(р-ра).
3. Следовательно, масса растворенного вещества
в полученном растворе вычисляется как сумма масс
веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = •m1(р-ра) +
•m2(р-ра).
4. Таким образом, массовая доля растворенного
вещества в полученном растворе равна:
или
или
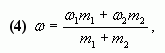
где — массы
соответствующих растворов.
Замечание: При решении задач удобно
составлять следующую таблицу.
|
1-й раствор |
2-й раствор |
Смесь двух растворов |
|
|
Масса растворов |
m1 |
m2 |
m1 + m2 |
|
Массовая доля |
|
|
|
|
Масса вещества в |
|
|
|
1.2. “Правило смешения”
Воспользуемся формулой (4):
тогда 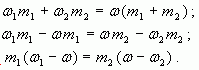
Отсюда
Таким образом, отношение массы первого
раствора к массе второго равно отношению
разности массовых долей смеси и второго раствора
к разности массовых долей первого раствора и
смеси.
Аналогично получаем, что при
Замечание: Формула (5) удобна тем, что на
практике, как правило, массы веществ не
отвешиваются, а берутся в определенном
отношении.
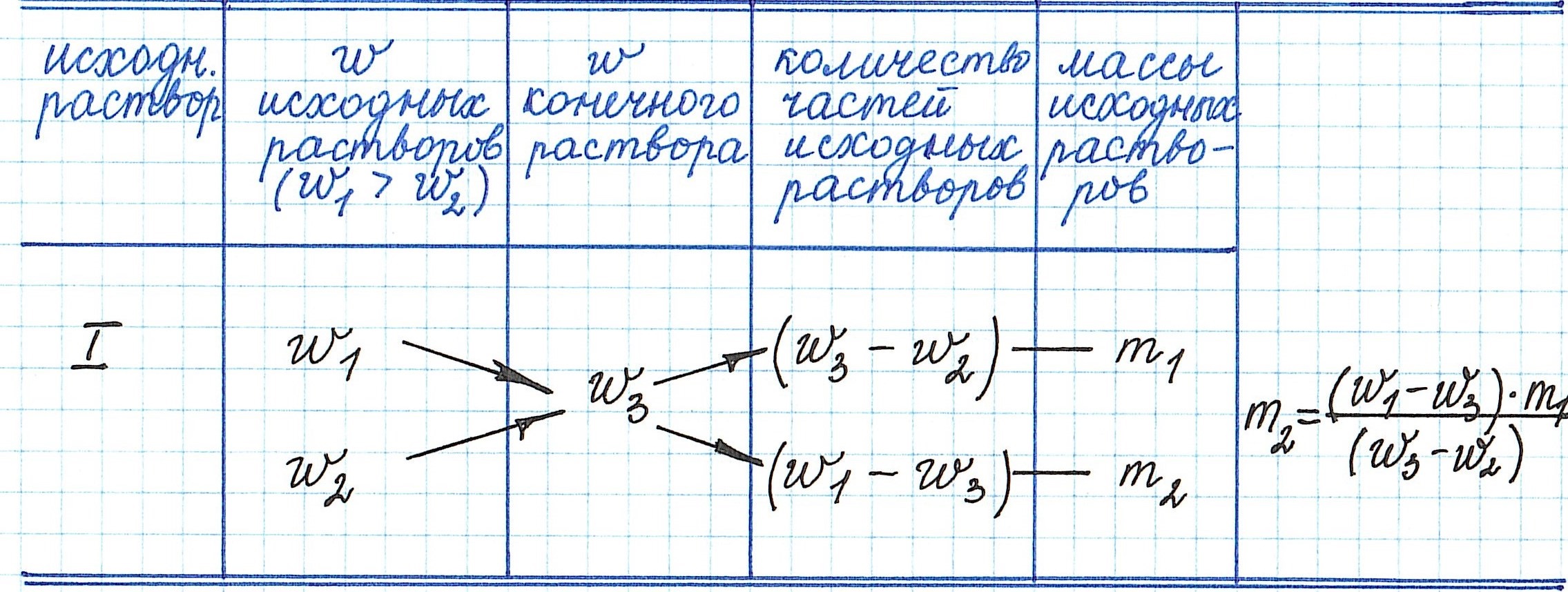
1.3. “Правило креста”
“Правилом креста” называют диагональную
схему правила смешения для случаев с двумя
растворами.
Слева на концах отрезков записывают исходные
массовые доли растворов (обычно слева
вверху-большая), на пересечении отрезков —
заданная, а справа на их концах записываются
разности между исходными и заданной массовыми
долями. Получаемые массовые части показывают в
каком отношении надо слить исходные растворы.
1.4. Графический метод
Отрезок прямой (основание графика)
представляет собой массу смеси, а на осях ординат
откладывают точки, соответствующие массовым
долям растворенного вещества в исходных
растворах. Соединив прямой точки на осях ординат,
получают прямую, которая отображает
функциональную зависимость массовой доли
растворенного вещества в смеси от массы
смешанных растворов в обратной пропорциональной
зависимости
Полученная функциональная прямая позволяет
решать задачи по определению массы смешанных
растворов и обратные, по массе смешанных
растворов находить массовую долю полученной
смеси.
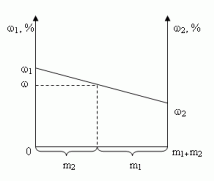
Построим график зависимости массовой доли
растворенного вещества от массы смешанных
растворов. На одной из осей ординат откладывают
точку, соответствующую массовой доли , а на другой —
. Обозначим на оси абсцисс
точки А и В с координатами (0,0) и (m1 + m2,0),
соответственно. На графике точка А(0,0)
показывает, что массовая доля всего раствора
равна , а точка В(m1
+ m2,0) — массовая доля всего раствора равна . В направлении от
точки А к точке В возрастает содержание в
смеси 2-го раствора от 0 до m1+ m2 и
убывает содержание 1-го раствора от m1+ m2
до 0. Таким образом, любая точка на отрезке АВ будет
представлять собой смесь, имеющую одну и ту же
массу с определенным содержанием каждого
раствора, которое влияет на массовую долю
растворенного вещества в смеси.
Замечание: Данный способ является наглядным
и дает приближенное решение. При использовании
миллиметровой бумаги можно получить достаточно
точный ответ.
1.5. Алгебраический метод
Задачи на смешивание растворов решают с
помощью составления уравнения или системы
уравнений.
2. Примеры решения задач
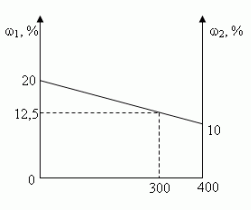
Задача 1. (№1.43, [1])
В 100 г 20%-ного раствора соли добавили 300 г её
10%-ного раствора. Определите процентную
концентрацию раствора.
Решение:
- C помощью расчетной формулы
- Графический
- Путем последовательных вычислений
- Сколько растворенного вещества содержится:
- Сколько вещества содержится в образовавшемся
растворе? - Чему равна масса образовавшегося раствора?
- Какова процентная концентрация полученного
раствора? - Алгебраический
Ответ: 12,5%
а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]
б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]
20 г + 30 г = 50 г
100 г + 300 г = 400 г
(50/400)100 = 12,5(%)
Ответ: 12,5%
Пусть х — процентная концентрация
полученного раствора. В первом растворе
содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в
полученном растворе х•(100 + 300)(г) соли.
Составим уравнение:
0,2•100 + 0,1•300 = х•(100 + 300);
х = 0,125 (12,5%)
Ответ: 12,5%
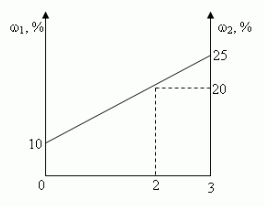
Задача 2. u(№10.26, [1])
Смешали 10%-ный и 25%-ный растворы соли и получили 3
кг 20%-ного раствора. Какое количество каждого
раствора в килограммах было использовано?
Решение:
- Алгебраический
- Графический.
- “Правило смешения”
- “Правило креста”
а) C помощью уравнения:
Пусть х (кг) — масса 1-го раствора, тогда 3-х (кг)
-масса 2-го раствора.
0,1•х (кг) содержится соли в 1-ом растворе,
0,25•(3-х) (кг) содержится соли в 2-ом растворе,
0,2•3 (кг) содержится соли в смеси.
Учитывая, что масса соли в 1-ом и 2-ом растворах
равна массе соли в смеси, составим и решим
уравнение:
0,1•х + 0,25•(3-х) = 0,2•3;
0,15х = 0,15;
х = 1, 1кг-масса 1-го раствора
3 — х = 3 — 1 =2 (кг) — масса 2-го раствора.
Ответ: 1 кг, 2 кг.
б) С помощью системы уравнений
Пусть х (кг) — количество первого раствора, у (кг)
— количество второго раствора. Система уравнений
имеет вид:
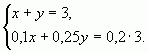
Ответ: 1 кг, 2 кг.
Ответ: 1кг, 2кг.

Составим диагональную схему
Ответ: 1кг, 2кг.
Задача 3 ([2])
Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму)
раствора соли. Сколько литров 20%-ного раствора
такой же соли надо налить в сосуд, чтобы
процентное содержание соли в сосуде стало
наибольшим?
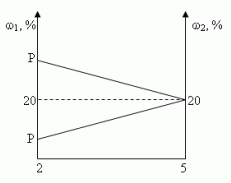
Решение (графический способ)
Заметим, что по условию, объём второго раствора
не превышает трёх литров.
- Ели р < 20, то для того, чтобы получить
максимальную массовую долю вещества в растворе,
необходимо добавить 3 л 20% — ного раствора соли; - Если р = 20, то при добавлении 2-го раствора,
процентное содержание соли в растворе не
изменится, следовательно, можно прилить от 0 л до 3
л 20% — ного раствора соли; - Если р > 20, то при добавлении 2-го раствора,
процентное содержание соли будет уменьшаться,
т.е. прилить нужно 0 л.
Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20
< р 100.
Задача 4 (работа 5, №2, [1])
В двух сосудах по 5л каждый содержится раствор
соли. Первый сосуд содержит 3л р% — ного раствора, а
второй — 4л 2р% — ного раствора одной и той же соли.
Сколько литров надо перелить из второго сосуда в
первый, чтобы получить в нем 10% — ный раствор соли?
При каких значениях р задача имеет решение?
Решение
Найдем, при каких значениях р задача имеет
решение. По условию задачи 5-ти литровый сосуд
содержит 3л первого раствора, следовательно, к
нему можно прилить от 0 до 2л второго раствора.
Имеем, Решая
неравенство, получаем
Ответ:
3. Заключение
Данные рекомендации предназначены учителям
математики, желающим организовать элективные
курсы, как в девятых, так и в десятых и
одиннадцатых классах. Цель создаваемых курсов:
научить учащихся пользоваться математическим
аппаратом при решении химических задач.
Список литературы
- Галицкий и др. Сборник задач по алгебре для 8-9
классов: Учебное пособие для учащихся шк. и
классов с углубл. изуч. математики / М.Л. Галицкий,
А.М. Гольдман, Л.И. Звавич.-2-е изд. — М.:
Просвещение,1994. — 271с. - Сборник задач по математике для поступающих в
вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С.
Иванов и др.; Под ред. А.И. Прилепко. — М.:Высш. школа,
1983. — 239 с. - Ерыгин Д.П., Шишкин Е.А. Методика решения задач по
химии: Учебное пособие для студентов пед. ин-тов
по биол. и хим. спец. — М.: Просвещение,1989. — 176с. - Хомченко Г.П., Хомченко И.Г. Задачи по химии для
поступающих в вузы: Учебное пособие. — 2-е изд..
исправ. и доп. — М.: Высш. школа, 1993. — 302 с.
Формула концентрации раствора. Их множество. И каждая соответствует тому или иному способу выражения концентрации. А в химии их применяются достаточно: массовая доля растворенного вещества, молярная, нормальная, моляльная, титр и др.
Зачем так много? Ответ на этот вопрос очень прост. Каждый вид концентрации удобен в том или ином случае, когда применение другого вида концентрации неуместно.
Например, при исследовании содержания массы вещества в очень небольшом объеме раствора удобно пользоваться титром. А в каких-то технологиях вообще концентрация заменяется другими количественными характеристиками раствора. Так, в технологии посола рыбы для расчета необходимой концентрации тузлука (раствора поваренной соли) используют не его процентную концентрацию, а плотность.
Содержание:
1. Концентрация – что это такое
2. Формула концентрации раствора: основные виды
3. Массовая доля растворенного вещества и примеры ее вычисления
- разбавление раствора водой
- концентрирование раствора путем упаривания
- концентрирование раствора путем добавления растворенного вещества
- смешивание двух растворов
- применение кристаллогидратов для приготовления раствора (задачи на кристаллогидраты)
4. Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Концентрация – что это такое
Любой раствор имеет различные характеристики: качественные и количественные. Одной из важнейших количественных характеристик является концентрация раствора.
Концентрация раствора – это количество растворенного вещества, содержащееся в определенном количестве раствора.
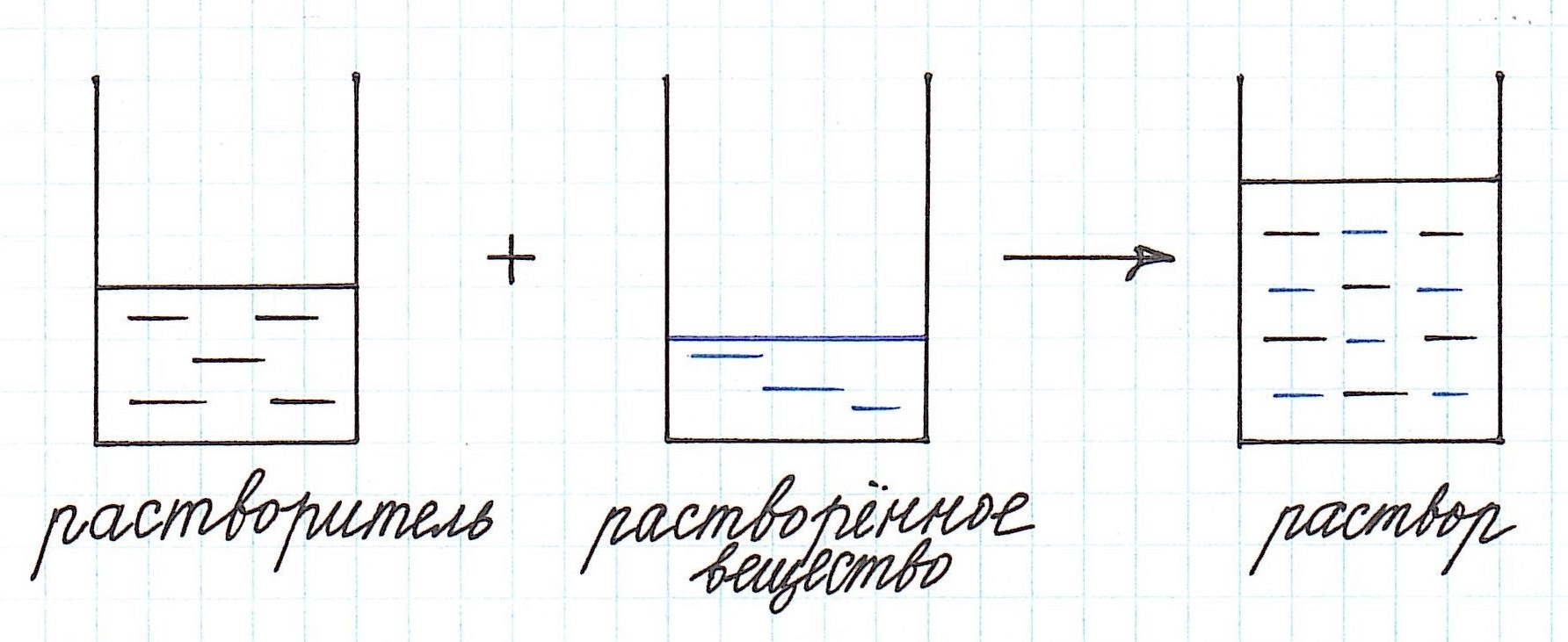
Как видно из приведенного определения, основными компонентами раствора являются:
— растворитель;
— растворенное вещество.
Растворенного вещества в растворе всегда меньше, а растворителя больше.
И вот именно с вычислением количественного содержания растворенного вещества чаще всего и связаны все расчеты, основанные на применении формулы концентрации раствора.
Существует несколько видов концентрации раствора:
— массовая доля растворенного вещества;
— объемная доля растворенного вещества;
— молярная доля растворенного вещества;
— молярная (или молярность);
— моляльная (или моляльность);
— нормальная (или эквивалентная);
— титр.
Формула концентрации раствора: основные виды
Применение того или иного вида концентрации уместно в каждом конкретном случае. Не существует какой-то универсальной концентрации или универсальной формулы концентрации раствора.
Кстати, с помощью математических преобразований можно перейти от одной концентрации к другой или найти взаимосвязь между разными их видами.
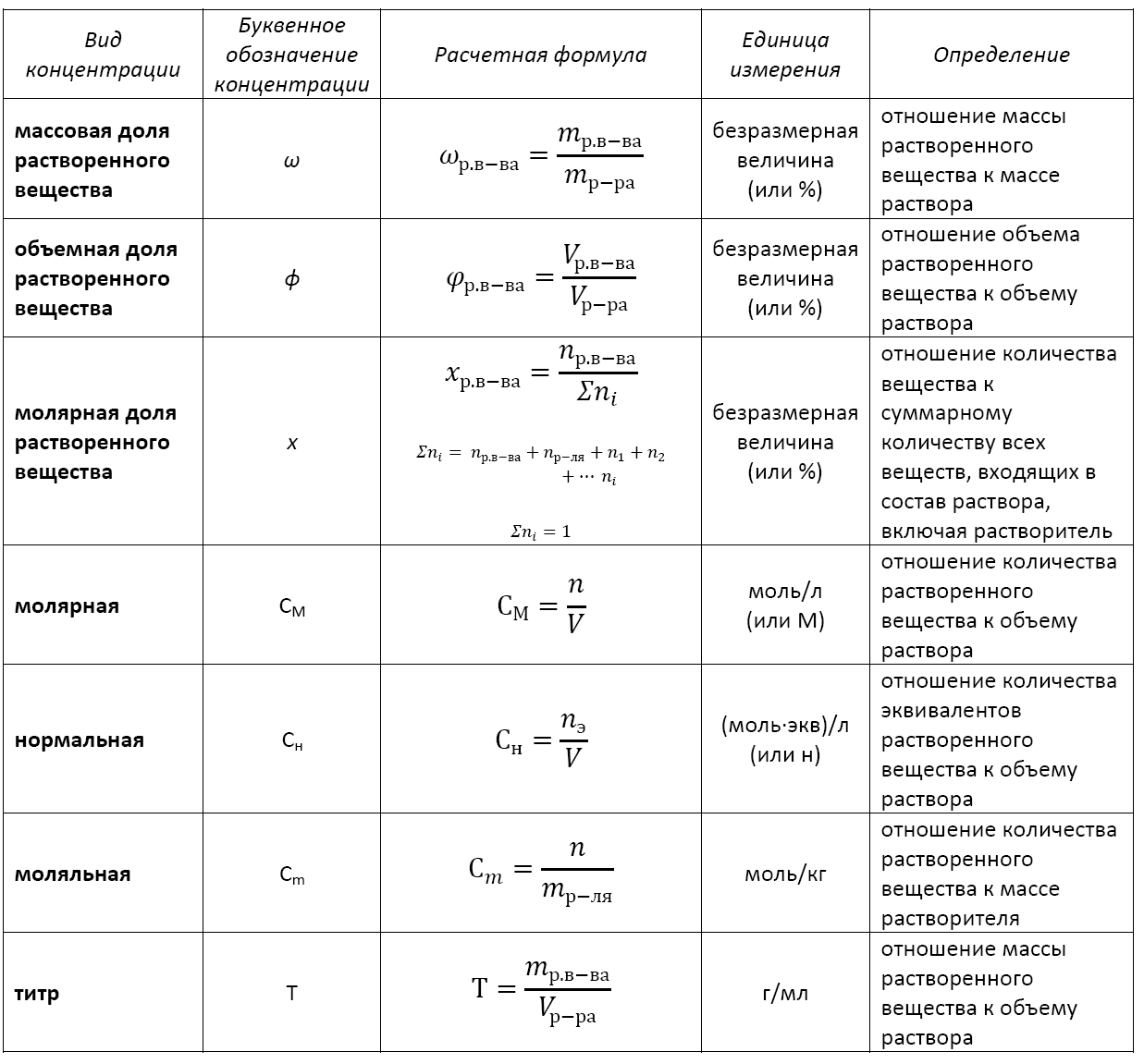
Основные расчетные формулы концентрации раствора приведены в таблице:
Массовая доля растворенного вещества и примеры ее вычисления
Массовая доля растворенного вещества – это отношение массы растворенного вещества к массе раствора.
Ее расчетная формула выглядит так:
где ωр.в-ва – массовая доля растворенного вещества, mр.в-ва – масса растворенного вещества, mр-ра – масса раствора.
ωр.в-ва представляет собой долю или от единицы или от 100%. Так, например, имеется двухпроцентный раствор NaCl. Его концентрация будет записана в первом случае ω(NaCl) = 0,02, а во втором – ω(NaCl) = 2%. Форма записи основной сути не меняет. Можно записывать и так, и так.
Что же означает выражение ω(NaCl) = 0,02 или ω(NaCl) = 2%? Буквально следующее: в 100 г водного раствора поваренной соли содержится 2 г этой соли и 98 г воды.
Необходимо помнить, что раствор состоит из растворителя и растворенного вещества. Поэтому масса раствора будет состоять из массы растворителя и массы растворенного вещества:
Тогда основную расчетную формулу для массовой доли растворенного вещества можно преобразовать:
Очень часто в расчетах с процентной концентрацией используются плотность и объем раствора:
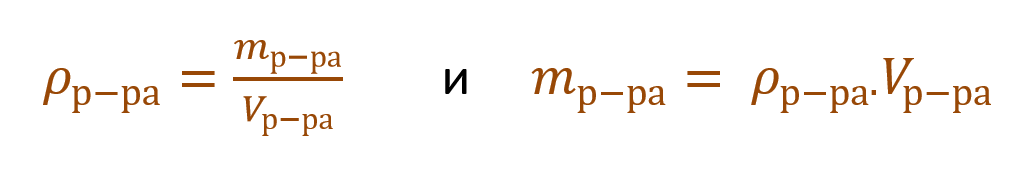
В других ситуациях могут использоваться объем и плотность не раствора, а растворителя. Тогда основная формула для расчета концентрации будет выглядеть так:
На практике бывает необходимо не только приготовить раствор с какой-либо определенной концентрацией, но и увеличить, либо уменьшить ее значение. Это достигается различными приемами:
— упариванием раствора;
— добавлением растворенного вещества;
— добавлением к раствору растворителя (например, воды).
Кроме того, приходится часто смешивать друг с другом растворы разных концентраций.
Разберем все возможные случаи.
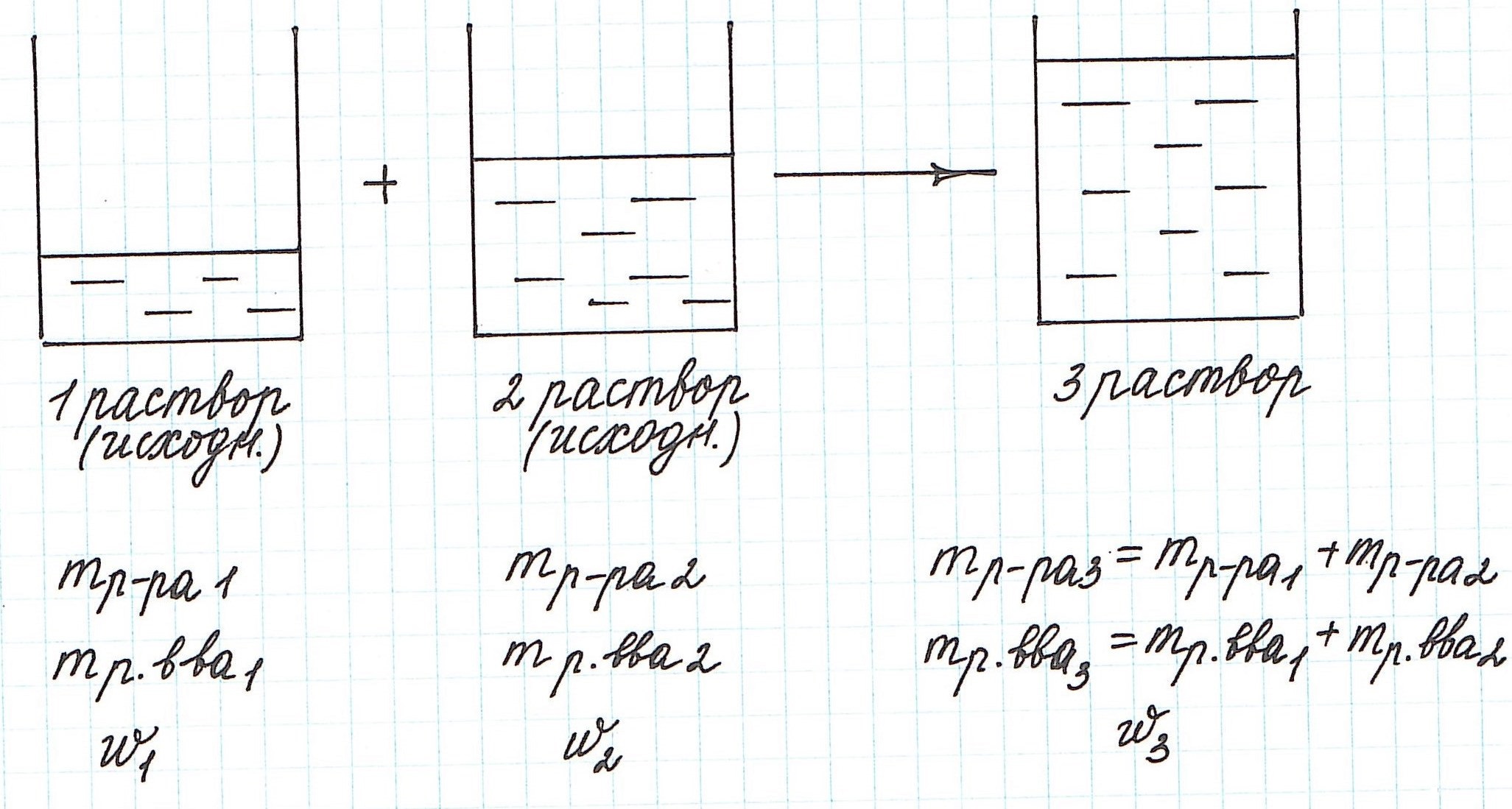
Мы рекомендуем задачи, в которых речь идет о растворах, решать с использованием схематических рисунков. Это очень наглядно, особенно, когда речь идет о смешивании растворов.
Начнем с самого простого: вычислим концентрацию раствора.
Пример 1. В 200 г воды растворили 40 г глюкозы. Вычислите массовую долю глюкозы в полученном растворе.
Обратите внимание, что речи о каком-либо химическом взаимодействии не идет! Поэтому записывать уравнения реакций не требуется!
Запишем общую формулу для расчета массовой доли растворенного вещества:
В данной задаче глюкоза (C6H12O6) – растворенное вещество, а вода (H2O) – растворитель. Масса раствора будет складываться из массы глюкозы и массы воды:
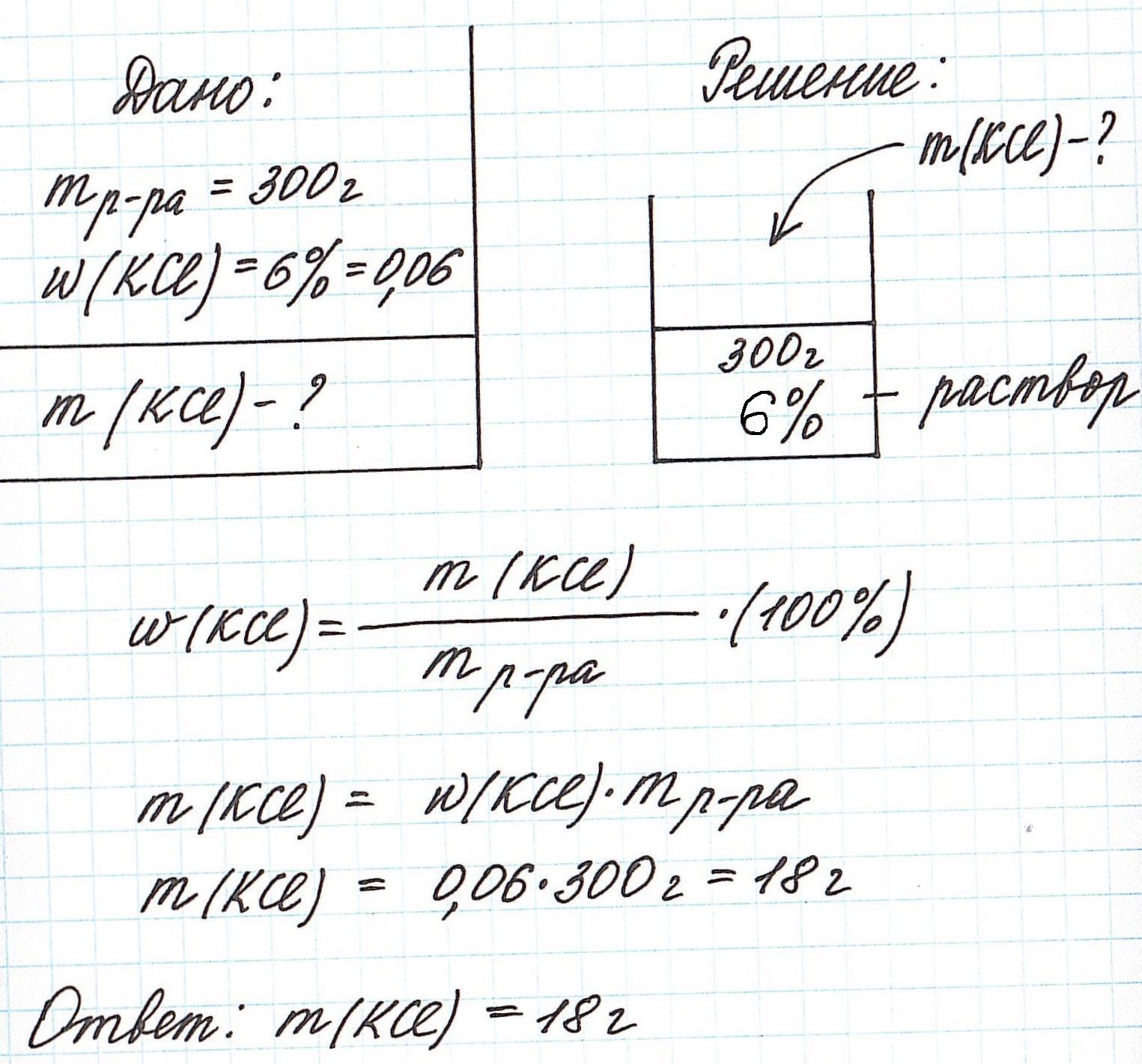
Пример 2. Рассчитайте, сколько потребуется хлорида калия, чтобы приготовить 300 г раствора с массовой долей соли 6%.
Обратите внимание, для того, чтобы расчеты были менее громоздкими, будем использовать выражение концентрации не в %, а в долях от единицы.
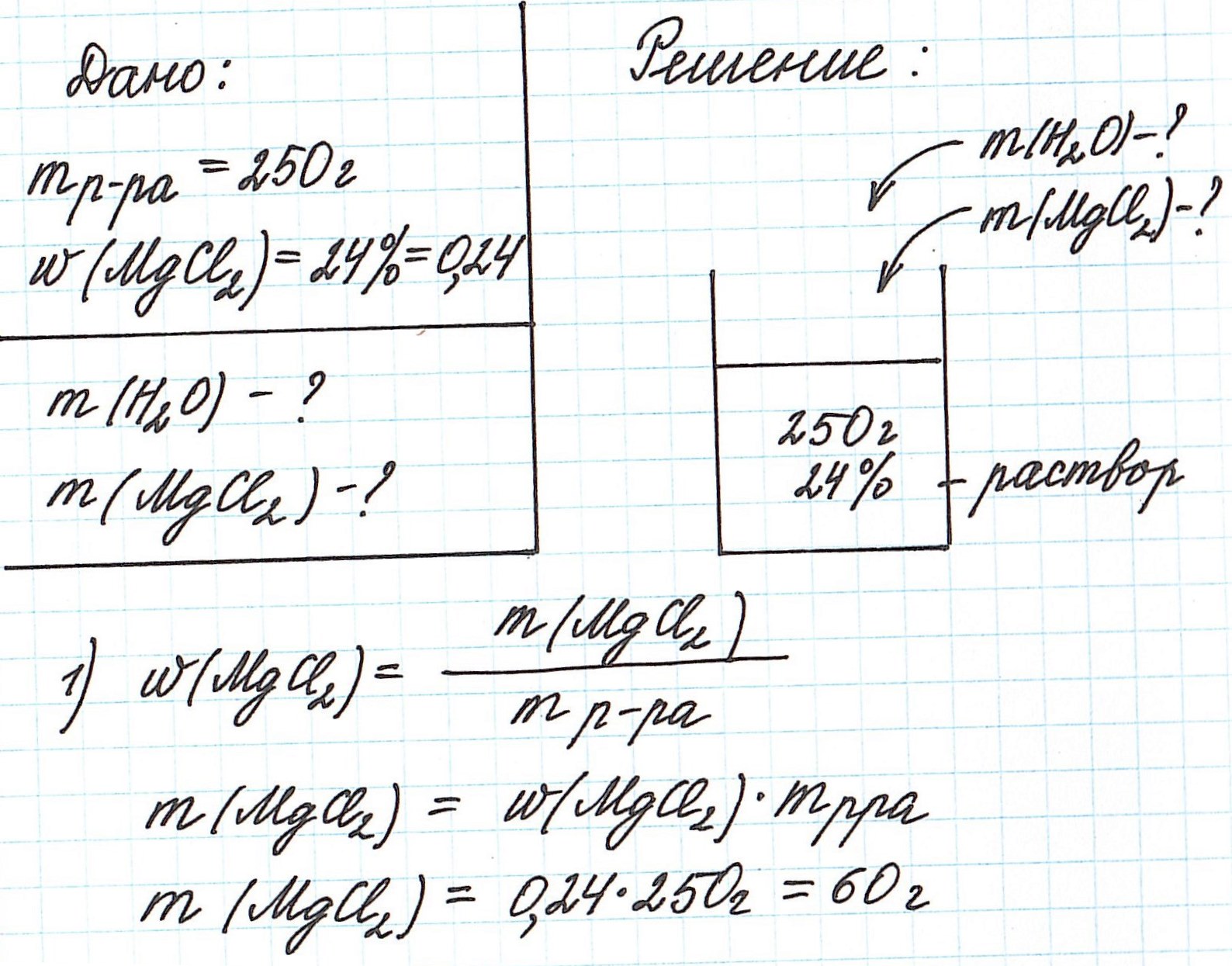
Пример 3. Необходимо приготовить 250 г раствора с массовой долей хлорида магния 24%. Рассчитайте массу требуемых воды и соли.
Так как раствор готовится из хлорида магния и воды, то и масса раствора равна сумме масс хлорида магния и воды:
Рассмотрим задачу, в которой в качестве растворителя выступает не вода, а другое вещество.
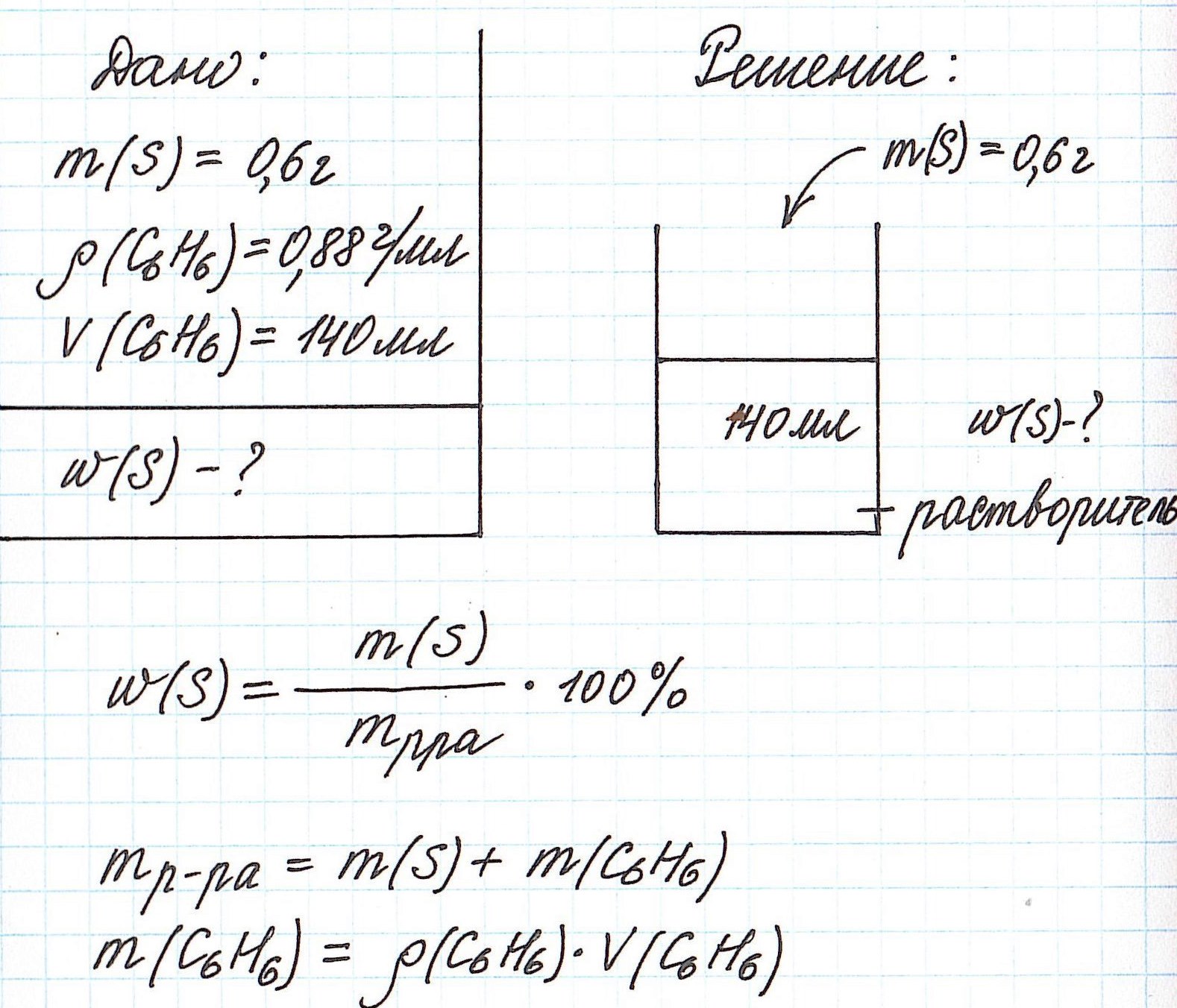
Пример 4. В органическом растворителе бензоле объемом 140 мл растворили серу массой 0,6 г. Вычислите массовую долю серы в полученном растворе, если плотность бензола составляет 0,88 г/мл.
Обратите внимание, что здесь:
— масса раствора не известна;
— масса растворителя (бензола) не известна;
— известны объем и плотность растворителя (бензола), что позволяет нам найти его массу;
— масса раствора состоит из массы растворителя (бензол) и массы растворенного вещества (сера).
Объединим все расчетные формулы в одну и подставим в нее имеющиеся численные значения:
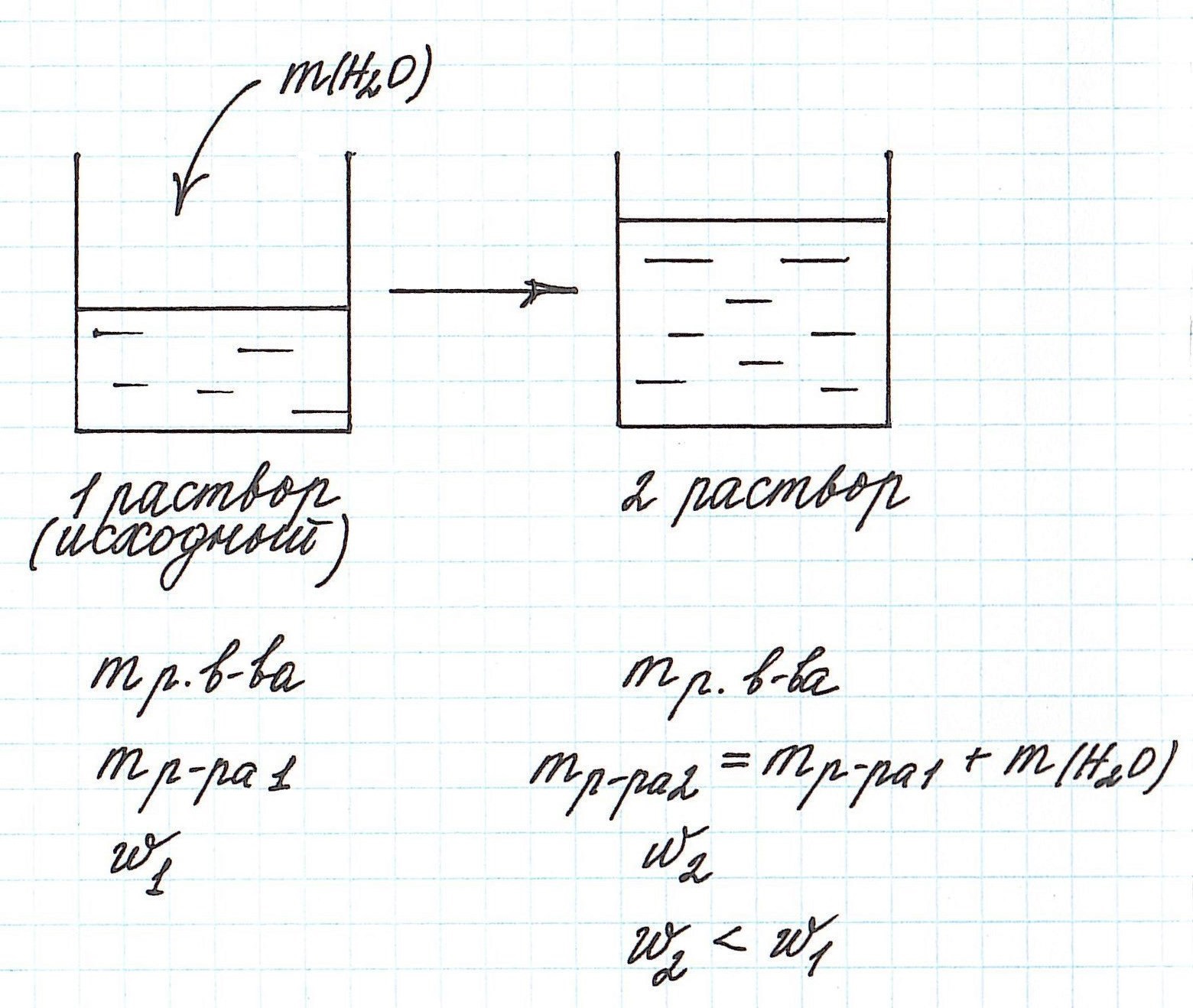
Вычисление массовой доли растворенного вещества при разбавлении раствора водой
Разбавление раствора водой приводит к уменьшению его концентрации.
Запомним, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворителя;
— масса растворенного вещества остается постоянной.
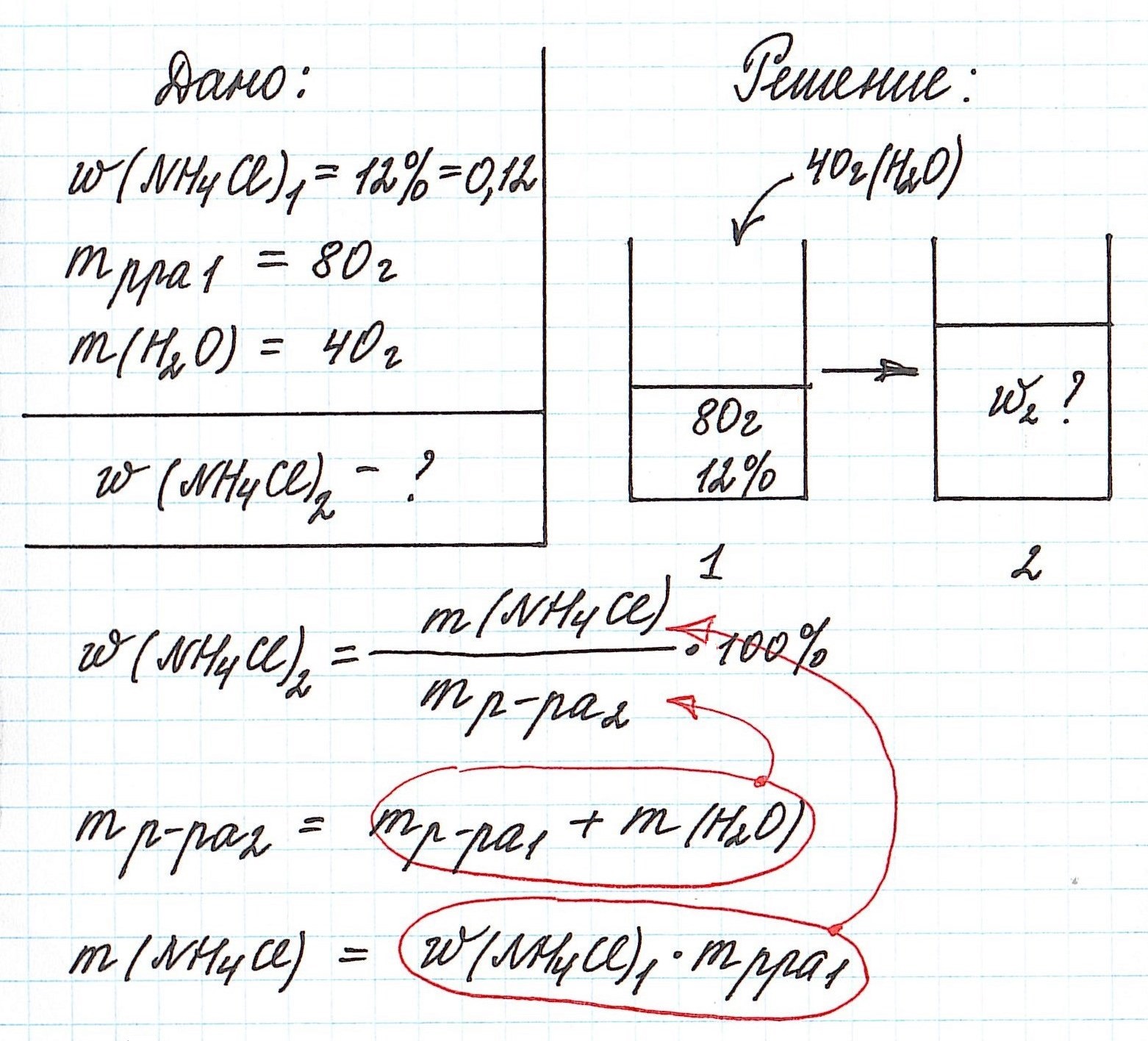
Пример 5. К 80 г раствора с массовой долей NH4Cl 12% добавили 40 г воды. Вычислите массовую долю хлорида аммония в полученном растворе.
Объединим все полученные формулы в одну и подставим имеющиеся данные:
Пример 6. Рассчитайте объем раствора фосфорной кислоты (массовая доля кислоты 12%, плотность 1,065 г/мл), который потребуется для приготовления раствора с массовой долей H3РO4 4% объемом 250 мл (плотность 1,02 г/мл).
В данной задаче речь напрямую о разбавлении раствора не идет. Но судя по тому, что исходный раствор имел концентрацию 12%, а конечный – 4%, становится ясно: последний раствор можно получить путем разбавления первого водой.
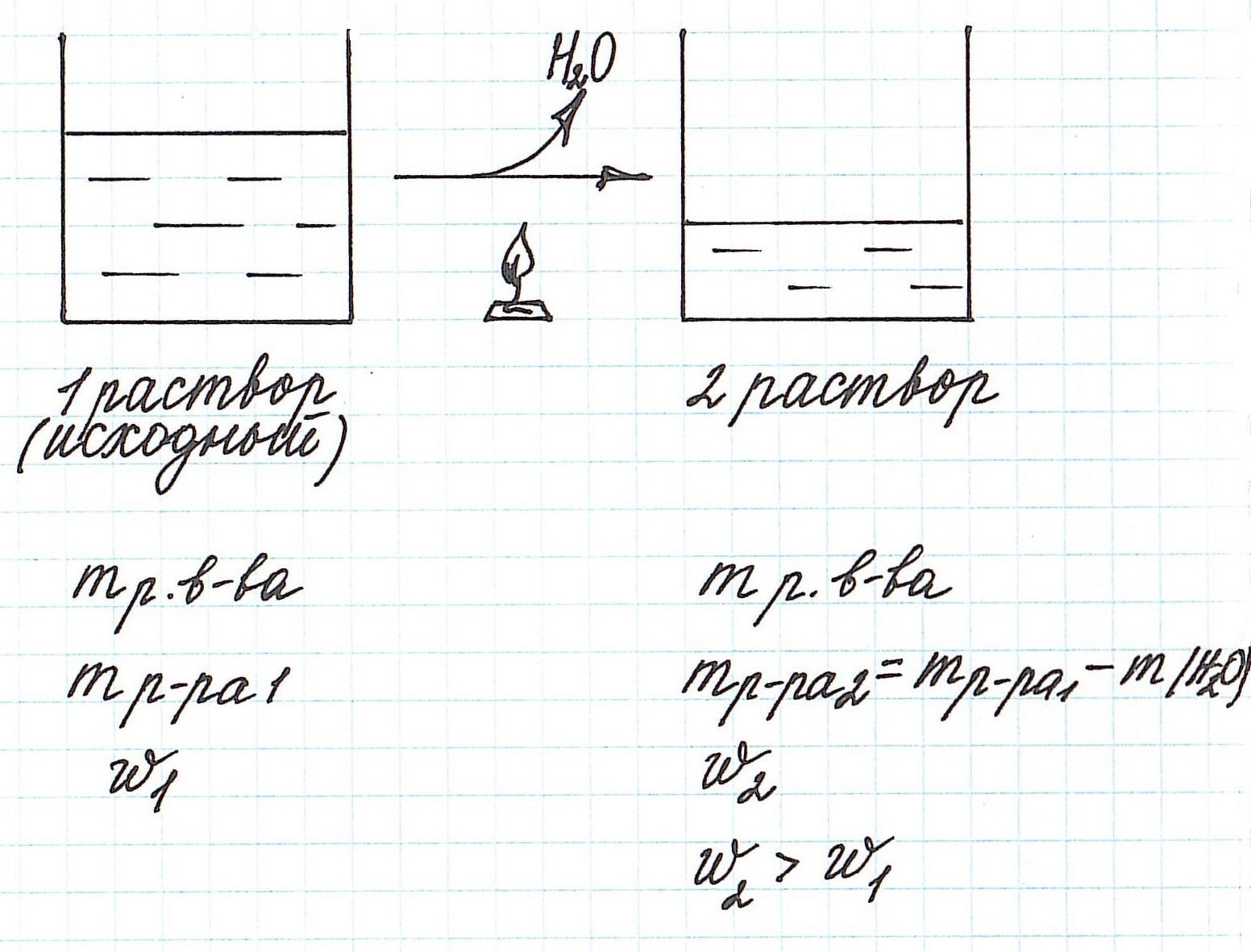
Вычисление массовой доли растворенного вещества при концентрировании раствора путем упаривания
Упаривание раствора, т.е. его нагревание, при котором происходит испарение воды, приводит к увеличению концентрации.
Учтите, что при этом:
— уменьшается масса раствора;
— уменьшается масса растворителя;
— масса растворенного вещества остается постоянной (при условии, что растворенное вещество не разлагается при данной температуре).
Пример 7. Из 200 г 27%-ного раствора глюкозы выпарили 20 г воды. Определите массовую долю глюкозы в полученном растворе.
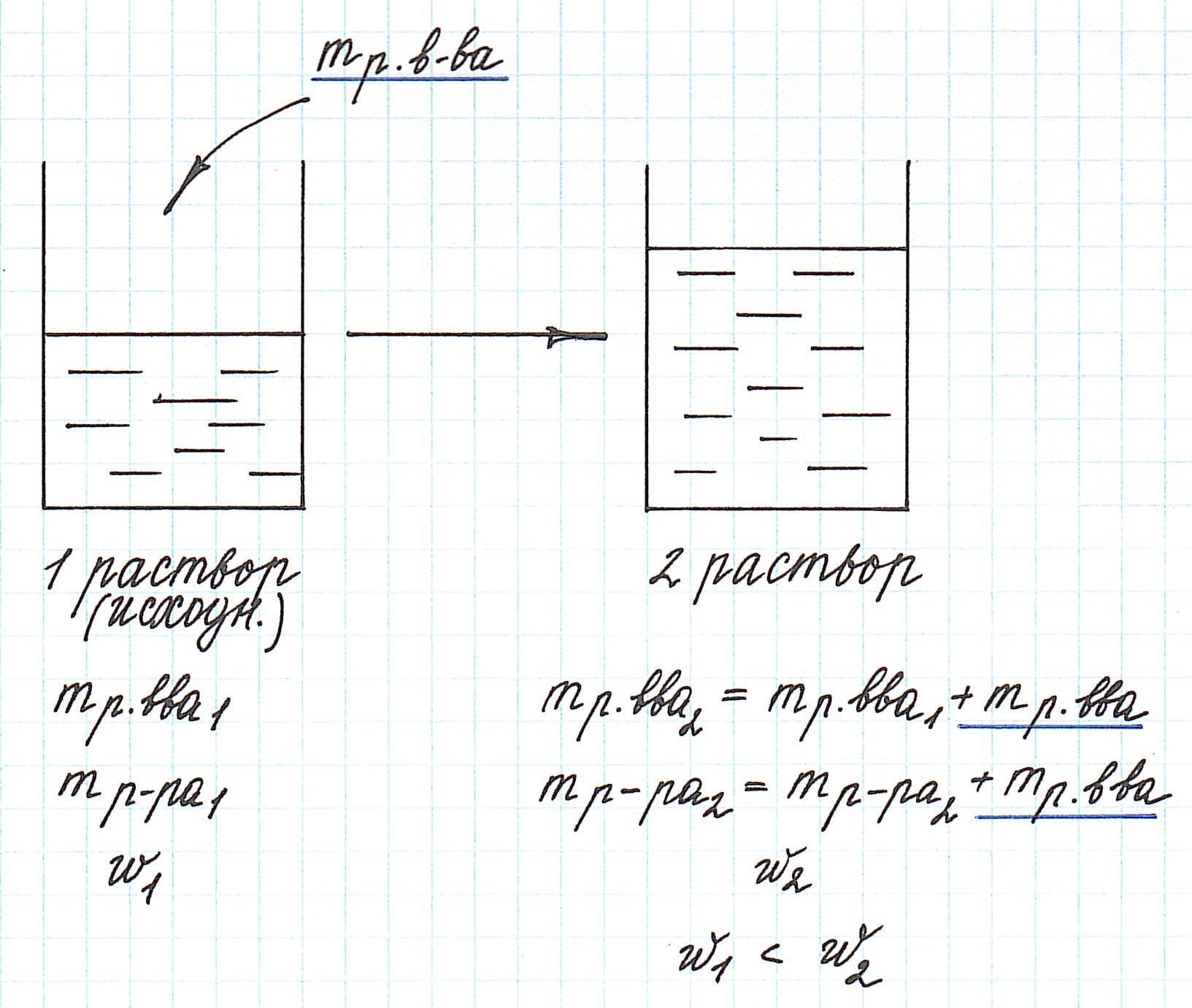
Вычисление массовой доли растворенного вещества при концентрировании раствора путем добавления растворенного вещества
Добавление к уже существующему раствору новой порции растворенного вещества приводит к увеличению концентрации раствора.
Помните, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества.
Пример 8. Определите массу хлорида калия, который надо добавить к 180 г 15%-ного раствора этой соли, чтобы получить 20%-ный раствор.
Вычисление массовой доли растворенного вещества при смешивании двух растворов
При смешивании двух растворов (речь о растворах одного и того же вещества конечно же) изменяются все количественные характеристики:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества;
— изменяется массовая доля растворенного вещества.
Пример 9. Смешали 80 г 32%-ного раствора и 30 г 10%-ного раствора нитрата меди (II). Какова концентрация соли в полученном растворе?
Вычисление массовой доли растворенного вещества с применением кристаллогидратов для приготовления раствора
Кристаллогидраты используются для приготовления растворов довольно часто. Кристаллогидраты представляют собой вещества, в состав которых помимо основного вещества входят молекулы воды. Например:
CuSO4·5H2O – кристаллогидрат сульфата меди (II) (или медный купорос);
Na2SO4·10H2O – кристаллогидрат сульфата натрия (или глауберова соль).
Больше примеров здесь.
Вода, входящая в состав кристаллогидрата, называется кристаллизационной.
Кристаллогидраты различаются прочностью связи между основным веществом и кристаллизационной водой. Одни из них теряют воду при комнатной температуре с течением времени и перестают быть кристаллогидратами (например, Na2СO3·10H2O). Другие – обезвоживаются только при сильном нагревании (например, CuSO4·5H2O).
При расчете концентрации с использованием кристаллогидратов для получения растворов часто приходится учитывать и кристаллизационную воду.
Но сначала поясним некоторые нюансы на конкретном примере:
1) Формула CuSO4·5H2O означает, что 1 моль CuSO4·5H2O содержит 1 моль CuSO4 и 5 моль H2O. Это можно было бы записать так:
n(CuSO4) = n(CuSO4·5H2O); n(H2O) = 5n(CuSO4·5H2O)
2) Относительная молекулярная (и численно молярная) масса будет складываться из относительной молекулярной массы вещества и относительной молекулярной массы воды. Например:
Mr(CuSO4·5H2O) = Mr(CuSO4) + 5·Mr(H2O) = 160 + 5·18 = 250 и, соответственно,
M(CuSO4·5H2O) = M(CuSO4) + 5·M(H2O) = 160 + 5·18 = 250 г/моль.
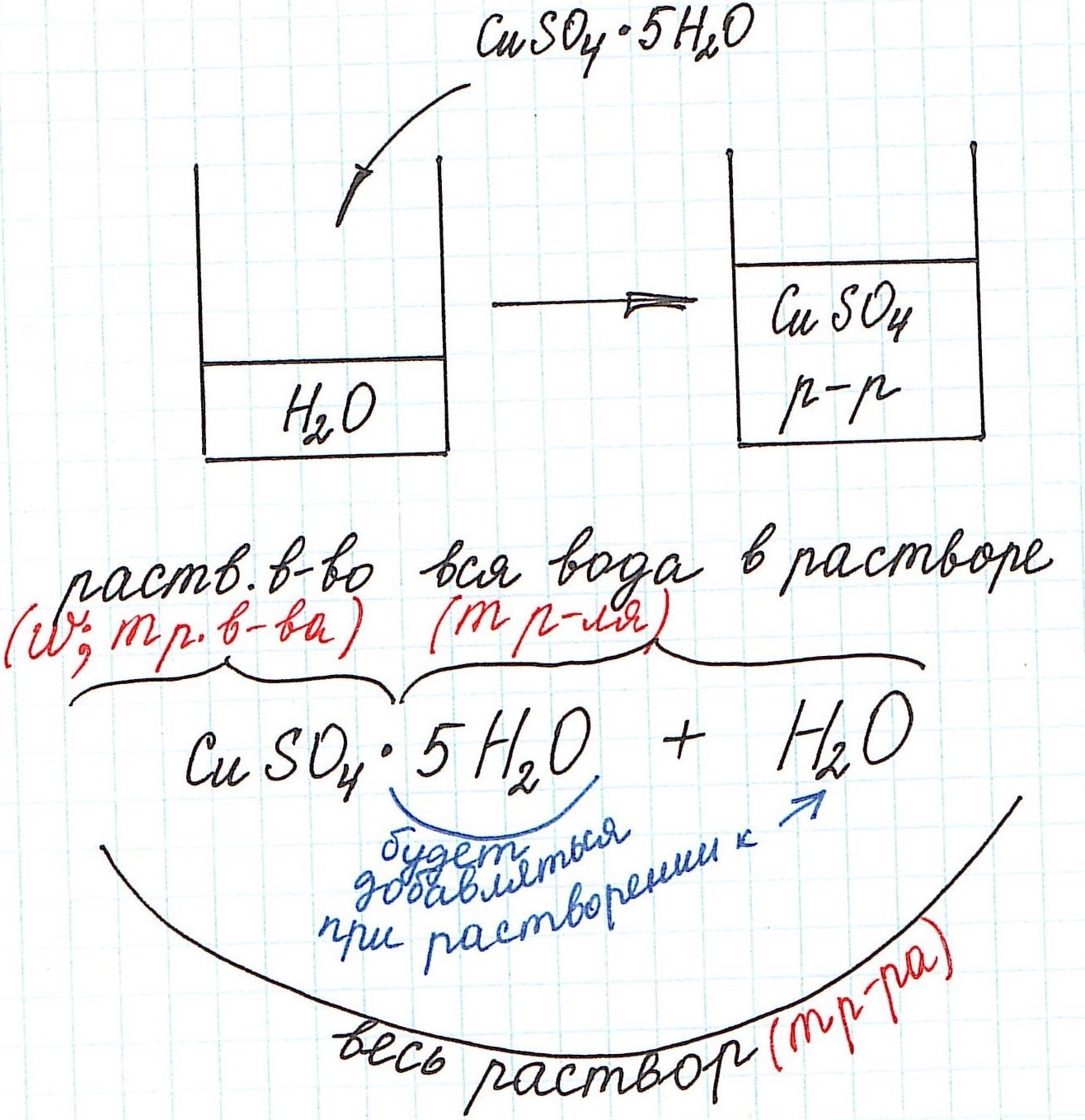
3) Еще одну особенность поясним с помощью рисунка:
Итак, разберем несколько типичных задач.
Пример 10. В 60 г воды растворили глауберову соль Na2SO4·10H2O массой 5,6 г. Какова массовая доля сульфата натрия в полученном растворе?
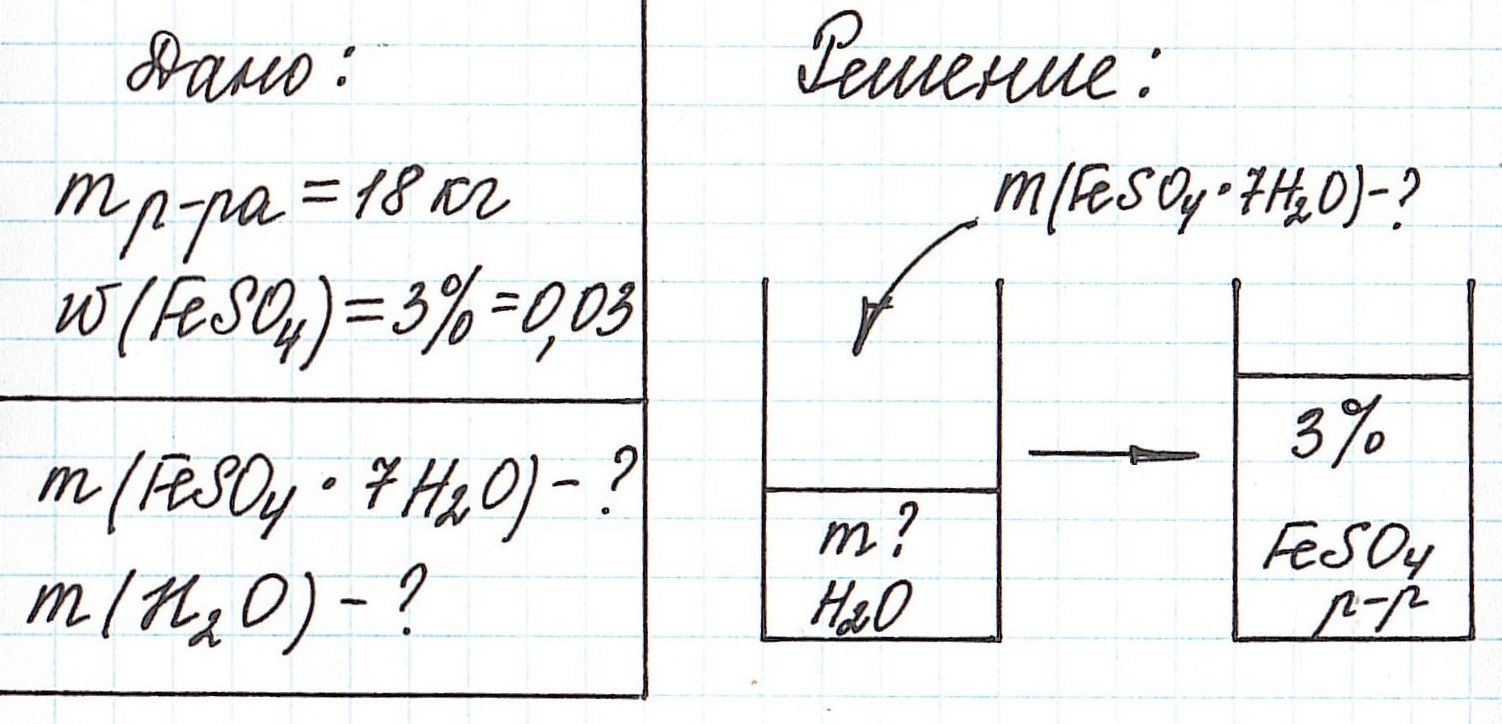
Пример 11. Какая масса железного купороса FeSO4·7H2O и воды потребуется для приготовления 18 кг раствора сульфата железа (II) с массовой долей FeSO4 3%?
Обратите внимание, что масса раствора дана не в граммах (г), а в килограммах (кг). Для того, чтобы привести в ходе расчетов все единицы измерения к единой системе, можно перевести килограммы в граммы и вычислять как обычно.
Но есть более простой способ. Можно считать количество вещества не в моль, а в киломоль (кмоль). Молярную массу вычислять не в г/моль, а в кг/кмоль. В этом случае ответ в задаче мы сразу получим в килограммах.
Пример 12. Вычислите массу кристаллогидрата сульфата никеля NiSO4·7H2O, который надо добавить к 180 г раствора с массовой долей сульфата никеля 1,5%, чтобы получить раствор с массовой долей соли 6%?
Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Правилом «креста» (или «квадратом Пирсона») очень удобно пользоваться в расчетах, связанных с разбавлением или смешиванием растворов.
Общая схема вычислений выглядит так:
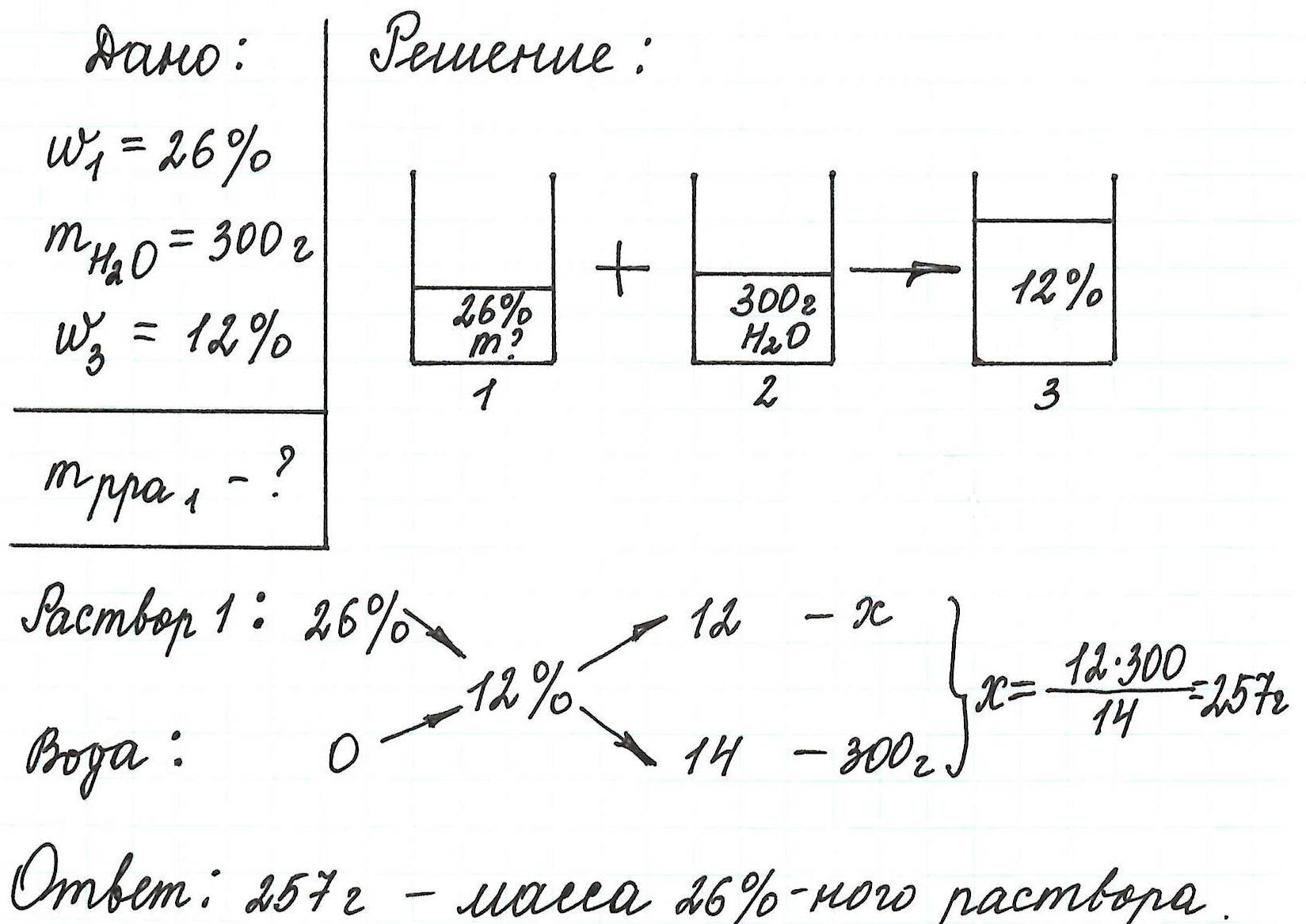
Пример 13. Какую массу 5%-ного раствора глюкозы надо добавить к 70 г 21%-ного раствора этого же вещества, чтобы получить 12%-ный раствор?
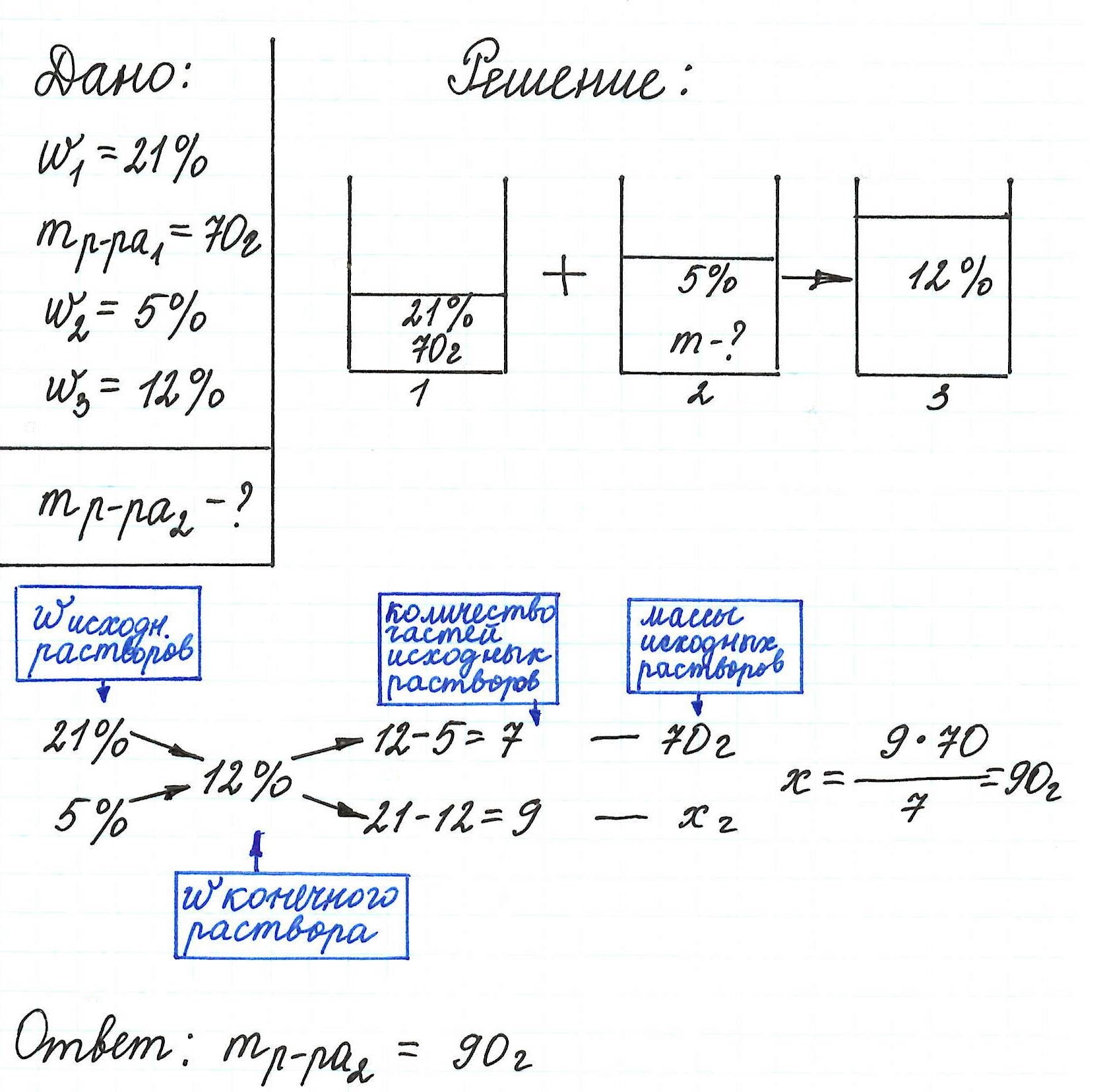
Еще примеры с применением правила «креста» можно посмотреть здесь.
Мы рассмотрели достаточно примеров расчетов, где используется формула такой концентрации раствора как массовая доля растворенного вещества. Как видим, ситуаций, в которых требуется ее применение, множество. Однако, есть достаточно случаев, когда более приемлемыми являются формулы других концентраций (молярной, нормальной, титра и т.д.). Об этом читайте в других статьях.
Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь к нашей группе ВКонтакте.
или на Одноклассниках
Пожалуйста, оцените публикацию. Большая просьба, если вы оцениваете публикацию от 1 до 3 звезд, обязательно оставьте свой комментарий с указанием того, что не так с этой публикацией. Мы постараемся устранить недостатки.
Ваше мнение для нас важно!
…
В данном разделе рассмотрены задачи на пересчет концентрации растворов, применение правила креста для нахождения концентрации при смешении и разбавлении растворов. Больше задач на расчет массовой доли растворенного вещества представлены в разделе подготовки к ОГЭ по химии.
Концентрация растворов и способы ее выражения
Задача 1. К 150 г 20% раствора сахарозы добавили 45 г глюкозы. Рассчитайте массовые доли углеводов в новом растворе.
Показать решение »
Решение.
Вначале сахарозы было 30 г:
20 г сахарозы содержится в 100 г раствора
х г — в 150 г
х =30 г
После прибавления глюкозы:
mобщ = m (сахарозы) + m (глюкозы) = 150 + 45 = 195 г
m раствора стала 195 г
Найдем полученные массовые доли сахарозы и глюкозы:
30 г сахарозы содержится в 195 г раствора
х г — в 100 г
х =15,4
ω2 (сахарозы) = 15,4%:
45 г глюкозы содержится в 195 г раствора
х г — в 100 г
х = = 23,1
ω2 (глюкозы) = 23,1%
Задача 2. Для нейтрализации 20 мл 0,1 н раствора кислоты потребовалось 6 мл раствора едкого натра. Определить нормальную концентрацию раствора едкого натра.
Показать решение »
Решение.
Согласно закону эквивалентов при нейтрализации в точке эквивалентности действует равенство, называемое Золотым правилом аналитики:
СН1×V1 = СН2×V2
0,1×20 = СН2×6
СН2 = 0,3 н.
Задача 3. Нормальная концентрация раствора KNO3 равна 0,2 моль/л. Найти процентную концентрацию раствора KNO3 и молярную концентрацию раствора KNO3. Плотность раствора принять раной 1 г/мл.
Показать решение »
Решение:
Найдем молярную массу и молярную массу эквивалента KNO3.
В данном случае, они совпадают.
М (KNO3) = 39+14+(16×3) = 101 г/моль
Найдем массу KNO3, содержащуюся в его 0,2 н. растворе:
1 н раствор KNO3 содержит – МЭ KNO3 в 1000 мл
Т.е. 1 н – 101 г
0,2 н. – х г
х = 20,2 г
Теперь вычислим молярную концентрацию
1М раствор KNO3 содержит – М KNO3 в 1000 мл
Т.е. 1 М – 101 г
х – 20,2 г
х = 0,2 моль/л
Таким образом, Сн = См = 0,2 моль/л
Далее находим процентную концентрацию.
Сначала необходимо рассчитать массу раствора объемом 1000 мл.
m = ρ×V = 1×1000 = 1000 г
тогда, решая пропорцию, находим:
20,2 г KNO3 содержится – в 1000 г раствора
х г – в 100 г раствора
х = 2,02 г
ω = 2,02%
Задача 4. Вычислите молярную и молярную концентрацию эквивалента (нормальность) 20 % раствора хлорида кальция плотностью 1,178 г/мл.
Показать решение »
Решение.
Найдем массу раствора
mр-ра = V·ρ = 1000 · 1,178 = 1178 г.
Найдем массу CaCl2, содержащуюся в 1178 г. 20 % раствора
20 г CaCl2 содержится в 100 г раствора
х г — в 1178 г раствора
х = 235,6 г.
Молярность определим с помощью соотношения:
См = n/V
n = m/M = 235,6/111 = 2,1 моль
M(CaCl2) = 40+35,5·2 = 111 г/моль
См = 2,1/1 = 2,1 М
Молярная концентрация эквивалента определяется с помощью соотношения:
Сн = nэ/V
Мэ = fэкв· М(CaCl2) = 1/2·111 = 55,5 г/моль
nэ = m/ Мэ = 235,6/55,5 = 4,2 моль
Сн = 4,2/1 = 4,2 н
Задача 5. Чему равна нормальность 30% раствора NaOH плотностью 1,328 г/мл? К 1 л этого раствора прибавили 5 л воды. Вычислите массовую долю полученного раствора.
Показать решение »
Решение.
Найдем массу NaOH, содержащуюся в 1328 г. 30 % раствора используя формулу:
ω(NaOH) = m (NaOH)/m
mр-ра = V·ρ = 1000 · 1,328 = 1328 г.
m(NaOH) = ω(NaOH) · m = 0,3 · 1328 = 398,4 г.
Найдем Молярную концентрацию эквивалента или нормальность:
M(NaOH) = 23+16+1 = 40 г/моль
Сн = nэ/V
Мэ = fэкв· М(NaOH) = 1·40 = 40 г/моль
nэ = m/ Мэ = 398,4/40 = 9,96 моль
Сн = 9,96/1 = 9,96 н
Найдем массу раствора после прибавления 5 л воды:
m2 = 1328 + 5000 = 6328 г
Далее находим процентную концентрацию или массовую долю вещества.
ω2(NaOH) = m (NaOH)/m2 = 398,4/6328 = 0,063 или 6,3 %
Задача 6. К 3 л 10 % раствора HNO3 плотностью 1,054 г/мл прибавили 5 л 2 % раствора той же кислоты плотностью 1,009 г/мл. Вычислите массовую долю в процентах и молярную концентрацию полученного раствора, объем которого равен 8 л.
Показать решение »
Решение.
Найдем массу растворов объемом 3 л и 5 л
m1= V1·ρ = 3000·1,054 = 3162 г
m2= V2·ρ = 5000·1,009 = 5045 г
Найдем массу HNO3, содержащуюся в 3162 г. 10 % раствора
10 г HNO3 содержится в 100 г ее раствора
х1 г — в 3162 г раствора
х1 = 316,2 г
Найдем массу HNO3, содержащуюся в 5045 г. 2 % раствора
2 г HNO3 содержится в 100 г ее раствора
х2 г — в 5045 г раствора
х2 = 100,9 г
При смешивании:
m (HNO3) = 316,2+100,9 = 417,1 г
mр-ра (HNO3) = 3162+5045 = 8207 г
Найдем Молярность
См = n/V
n = m/M = 417,1/63 = 6,62 моль
M(HNO3) = 1+14+16·3 = 63 г/моль
См= 6,62/1 = 6,62 М
ω(HNO3) = m (HNO3)/mр-ра = 417,1/8207 = 0,05 или 5 %
Задача 7. Определить молярность, нормальность, моляльность и титр 4 % раствора FeSO4 объем которого равен 1,5 л, плотность 1037 кг/м3
Показать решение »
Решение.
M (FeSO4) = 56+32+16·4 = 152 г/моль
Мэ = fэкв· М(FeSO4) = 1/2·152 = 76 г/моль
Найдем m раствора объемом 1,5 л
m = V·ρ = 1,5·10-3 ·1037 = 1,56 кг
Найдем m 4 % раствора
m(FeSO4) = ω(FeSO4) · mр-ра = 0,04·1,56 = 0,0624 кг = 62,4 г
Найдем молярность, которая определяется как количество молей растворенного вещества в одном литре раствора
n = m/М = 62,4/152 = 0,41 моль
См = n/V = 0,41/1,5 = 0,274 М
Найдем нормальность:
nэ = m/Мэ = 62,4/76 = 0,82 моль
Сн = nэ/V = 0,82/1,5 = 0,547 н
Моляльная концентрация равна:
b (x) = n(x)/m
Масса растворителя равна: mH2O = 1560-62,4 = 1497,6 г = 1,5 кг
b (FeSO4) = n(FeSO4)/m = 0,41/1,5 = 0,27 моль/кг
Титр определим следующим образом:
Т (х) = m (х)/V
Т (FeSO4) = m (FeSO4)/V = 62,4/1500 = 0,0416 г/мл
Задачи на смешение и разбавление растворов
Такие задачи можно решить с помощью правила креста или правила смешения. Суть его заключается в составлении «креста», в виде которого располагают две прямые линии. В центре пишут ту концентрацию, которую надо получить, у концов линий креста слева – концентрации исходных растворов (большую – сверху, меньшую — снизу), у концов линий креста справа – искомые концентрации (или массы) растворов, которые получают вычитанием по направлению линий из большей величины меньшей. В общем виде схема решения задач по правилу креста имеет вид:
Таким образом, следует взять mА грамм раствора с массовой долей а% и прибавить к нему mB грамм раствора с массовой долей b%. Если надо узнать, какие массы растворов данной концентрации следует взять, чтобы получить заданную массу раствора новой концентрации, то сначала определяют отношение mА и mB . Затем пропорционально этому отношению делят заданную массу.
Задача 8. Сколько граммов раствора с массовой долей серной кислоты 96% необходимо влить в 1 л воды, чтобы получить раствор с массовой долей 10%
Показать решение »
Решение.
Для решения данной задачи используем правило креста.
Чистый растворитель (воду) можно представить как раствор с массовой долей растворенного вещества 0%
Определим m раствора с ω (H2SO4) = 96%, который надо влить в 1 л воды:
10 г H2SO4 надо влить в 86 г воды
х г — 1000 г
х = 116,28 г
m (р-ра H2SO4) = 116,28 г
Задача 9. Сколько мл 0,5 М и 0,1 М растворов азотной кислоты следует взять для приготовления 1000 мл 0,2 М раствора.
Показать решение »
Решение.
По правилу креста, определяем в каких соотношениях следует взять 0,5 М и 0,1 М растворы азотной кислоты, чтобы получить раствор заданной концентрации:
V0.5/V0.1 = 0,1/0,3 = 1/3
Взяв 0,1 л и 0,3 л исходных растворов, получим 0,4 л 0,2 М раствора HNO3, но по условию задачи нужно получить 1 л. Для этого разделим 1 л на две части в соотношении 1:3, составив пропорции:
Для 0,5 М раствора HNO3
из 0,1 л 0,5 М раствора получим 0,4 л 0,2 М р-ра HNO3
х1 л — 1 л
х1 = 0,25 л
Для 0,1 М раствора HNO3
из 0,3 л 0,5 М раствора получим 0,4 л 0,2 М р-ра HNO3
х2 л — 1 л
х2 = 0,75 л
Правило Пирсона (оно же правило креста) предназначено для решения одной задачи: сделать раствор нужной концентрации из двух имеющихся растворов с различной концентрацией.
Следует отметить что оно актуально только для массовых концентраций. Это значит что менять граммы на миллилитры, или массовые доли на объемные доли нельзя. В таком случае нужно заменить объем на массу через плотность. В случае этилового спирта это можно сделать через калькулятор.
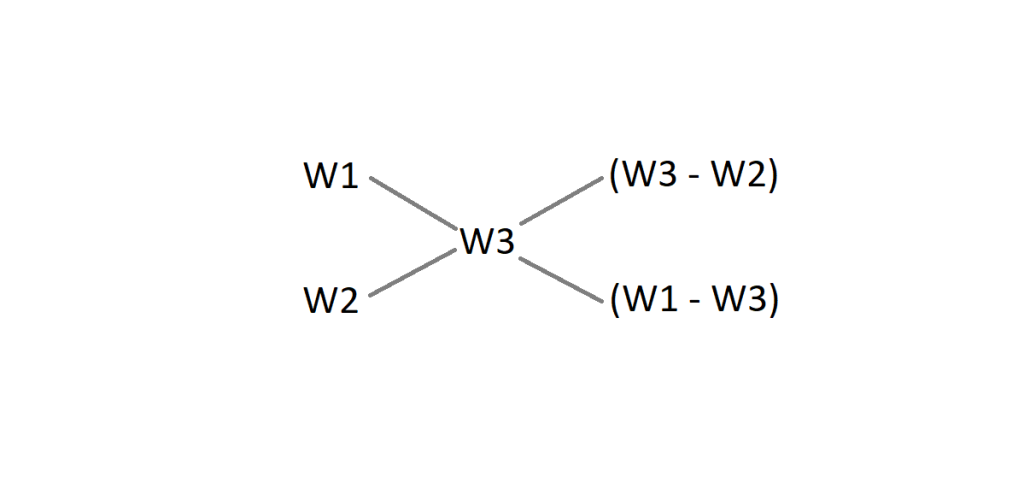
Выгладит правило следующим образом.
W1 — известная массовая доля первого вещества
W2 — известная массовая доля второго вещества
W3 — искомая массовая доля
Если одно из известных веществ это вода, которая является растворителем, то массовая доля будет равна нулю.
По диагонали находим разницу и получаем соотношение (сколько частей) в котором нужно взять первого раствора и второго раствора.
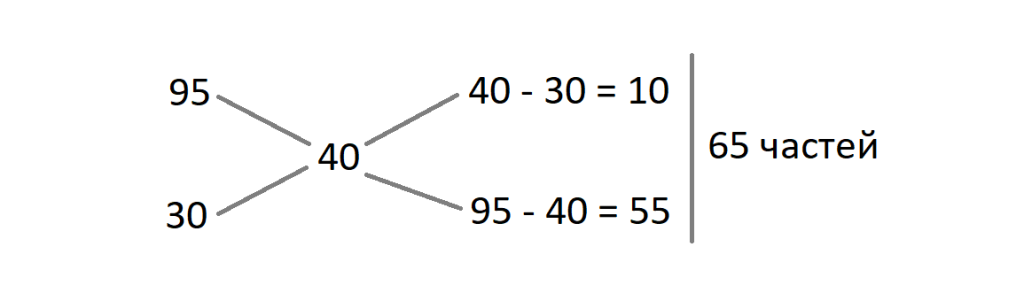
Пример 1.
Необходимо приготовить 500 грамм 40%(масс.) раствора спирта, имея в наличии 95%(масс.) и 30%(масс.) раствор.
1 массовая часть = 500 / 65 = 7.69 грамм
Масса 95%(масс.) раствора = 7.69 * 10 = 76.9 грамм
Масса 30%(масс.) раствора = 7.69 * 55 = 422.95 грамм
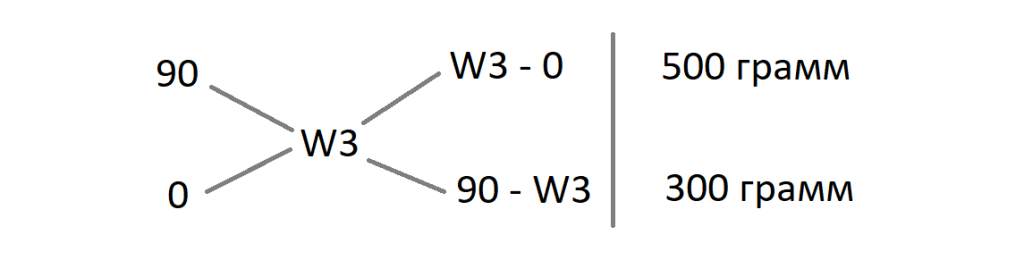
Пример 2.
Определить концентрацию раствора после смешивания 500 грамм 90%(масс.) спирта и 300 грамм воды.
Составим пропорцию: (W3 — 0) / (90 — W3) = 500 / 300 и решим уравнение. Получим W3 = 56.25%(масс.).
При разбавлении и концентрировании
растворов количество вещества (количества
вещества эквивалента) остается постоянным.
Пример 6. Какой объем раствора HCl,
С1(HCl) = 6 моль/л, необходимо
использовать для приготовления 250 мл
раствора этой кислоты с концентрацией
С2(HCl) = 2,5 моль/л.
Решение:
V(HCl) =
n(HCl) = const;
n(HCl) = C2(HCl)·V2 = 2,5·0,25 = 0,625 моль
V(HCl) =
= 0,104 л = 104 мл
Ответ: необходимо использовать 104
мл раствора.
Пример 7. До какого объема следует
упарить 3,5 л раствора серной кислоты,
С1(H2SO4) = 0,04 моль/л,
чтобы получить раствор с концентрацией
кислоты 0,2 моль/л.
Решение:
Величина n(H2SO4) определяется
из данных условия:
n(H2SO4) = n(H2SO4)·
= С1(H2SO4)·
·V
= 0,04··3,5
= 0,07 моль
Отсюда V =
=
= 0,35 л = 350 мл
Ответ: исходный раствор следует
упарить до объема 350 мл.
2. 3. Расчеты, связанные со смешиванием растворов различной концентрации
При смешивании растворов количество
вещества n(X) (количества вещества
эквивалента) в полученном растворе
равно сумме количества вещества
(количества вещества эквивалента) в
смешиваемых растворах n 1(X), n
2(X) … n n(X):
n(X) = n 1(X) + n 2(X) + n 3(X) +…+
n n(X),
При смешивании растворов объем
полученного раствора не равен сумме
объемов смешиваемых растворов. Это
явление называют контракцией растворов.
Поэтому объем полученного раствора
следует рассчитывать.
При решении задач на смешивание растворов
часто приходится производить перерасчет
одной концентрации в другую.
Пример 8. Рассчитать массовую долю
1,25 н. раствора фосфорной кислоты, если
плотность раствора составляет 1,05 г/мл.
Решение:
ω(H3PO4) =
Объем раствора принимаем за 1 л (1000 мл).
Тогда масса раствора равна:
m(р-ра) = V·ρ = 1000·1,05 = 1050 г
Фактор эквивалентности H3PO4
=
Количество вещества: n(H3PO4)
= C(H3PO4)·V
= 1,25·1 = 1,25 моль
Масса H3PO4 в растворе:
m(H3PO4) = n(H3PO4)·M(
H3PO4)
= n(H3PO4)·
·M(H3PO4)
m(H3PO4) = 1,25··98
= 40,83 г
Массовая доля H3PO4 в растворе:
ω(H3PO4) =
= 0,039 или 3,9%
Ответ: ω(H3PO4) = 0,039 или
3,9%.
Пример 9. Смешали 3 литра раствора
H3PO4 (C(H3PO4) = 0,1 моль/л)
и 2 литра раствора H3PO4
(ω(H3PO4) = 90%, ρ = 1,05 г/мл). Вычислить
молярную концентрацию и молярную
концентрацию эквивалента полученного
раствора (контракцией можно пренебречь).
Решение:
Фактор эквивалентности H3PO4
=
С(H3PO4) =
С(H3PO4)
=
= 3·С(H3PO4)
Поскольку по условию задачи контракцией
пренебрегаем, то:
V = V1 +V2 = 3,0 + 2,0 = 5,0 л
Количества вещества в полученном
растворе определяется по формуле:
n(H3PO4) = n1(H3PO4)
+ n2(H3PO4)
Количества вещества в первом исходном
растворе:
n1(H3PO4) = C(H3PO4)·V1
= 0,1·3 = 0,3 моль
Количества вещества во втором исходном
растворе:
n2(H3PO4) =
=
=
= 1,928 моль
Отсюда n(H3PO4) = 0,3 + 1,928 = 2,228
моль
С(H3PO4) =
= 0,446 моль/л
С(H3PO4)
= 3·0,446 = 1,337 моль/л
Ответ: молярная концентрация
полученного раствора H3PO4
равна 0,446 моль/л, молярная концентрация
эквивалента этого раствора равна 1,337
моль/л.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #