Как найти концентрацию смеси в математике

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

• повторить понятия проценты, отношения;
• закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
• показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

• показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
• воспитание у учащихся интереса к предмету.

Развивающие

• развивать наблюдательность, логическое мышление учащихся;
• развивать жизненную смекалку и интуицию.

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.

План урока:

1. Мотивационный момент (1 минута).
2. Подготовка учащихся к сознательному усвоению нового материала (5 минут).
3. Изучение нового материала (12 минут).
4. Решение задач на отработку формул (3 мин).
5. Физминутка (1 минута).
6. Первичное закрепление нового материала (15минут).
7. Рефлексия (1 минута).
8. Подведение итогов. Домашнее задание (2 минуты).

Ход урока

I. Мотивационный момент.

Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.

II. Подготовка к сознательному усвоению нового материала.

(Слайд 2)

1. Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
2. Указать в виде процентов: 0,7; 0,04; 1,3.
3. Найти 15% от числа 60.
4. Найти число, 15% которого равны 30.
5. Из 25 семян взошло 24 семени. Найдите процент всхожести.
6. Итак, известные нам отношения: (Слайд 3)

Всхожесть = ; .

Значения данных отношений мы представляли в виде процентов.

III. Изучение нового материала.

Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?

В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].

Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].

Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)

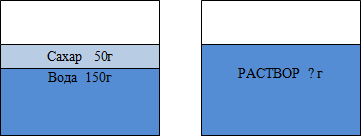
Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

50+150=200 (г) – масса общая. (Слайд 5)

Раствор тщательно перемешиваем.

Найдите процентное содержание сахара в растворе.

50 : 200=1: 4 = 0,25;

0,25=25%

25% – процентное содержание сахара в данном растворе.

Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)

Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).

Концентрация = , т.е. К=.

Как по этой формуле найти М_ч.в? М_общ?

М_ч.в. = М_общ · К

М_общ = Мч.в: К

(Слайд 7)

IV. Решение задач на отработку формул:

(Слайд

1. В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
2. 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
3. Какова масса раствора, в котором 150 г сахара составляют 25%.

Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)

Рис.1.

Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».

Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.

V. Физминутка.

(Слайд 11)

Следите глазами за движениями черепашек.

VI. Первичное закрепление нового материала.

Решим несколько задач на «концентрацию».

(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.

Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)

Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.

Решение:

1. Какова масса раствора в первой банке?
   480+120 = 600 (г)

2. Какова концентрация сахара в растворе первой банки?
   120:600 = 0,2; 0,2=20%

3. Какова масса раствора во второй банке?
   840+160 = 1000(г)

4. Какова концентрация сахара в растворе второй банки?
   160:1000 = 0,16; 0,16=16%

5. В какой банке вода слаще?
   20% > 16%

Ответ: в первой банке вода слаще.

Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)

Решение:

80% – это процентное содержание соли в 200г раствора (концентрация 0,8)

1. Сколько г соли в этом растворе?
   0,8 ·200=160(г)

20% – это содержание соли в 700 г раствора (концентрация соли 0,2)

1. Сколько г соли во втором растворе?
   0,2·700=140 (г)
2. Сколько г соли в полученном растворе?
   160+140=300 (г)

Ответ: 300 г.

Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)

Решение:

50% – процентное содержание соли в 200 г растворе (концентрация 0,5).

1. Сколько г соли в этом растворе?
   0,5·200=100 (г)
   Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25)

2. Какова масса второго раствора?
   150:0,25= 600 (г)
   Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора.

3. Какова масса соли в двух растворах?
   100+150=250 (г)

4. Какова масса нового раствора?
   200+600 =800 (г)

5. Какова концентрация соли в новом растворе?
   250:800=0,3125; 0,3125 = 31,25%

Ответ: 31,25%.

Задача для самостоятельного решения (дома).

Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]

Решение:

1. Сколько кг соли в морской воде?
   0,05·30=1,5 (кг)
   Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015.

2. Какова масса нового раствора (с добавлением пресной воды)?
   1,5: 0,015= 100 (кг)

3. Сколько пресной воды нужно добавить?
   100 – 30 = 70 (кг)

Ответ: 70 кг.

VII. Этап рефлексии.

(Слайд 18)

Ответ на листочке:

• Сегодня я узнал….
• У меня получилось…
• Было трудно….
• Было интересно….
• Теперь я умею…

VIII. Итог урока. Домашнее задание.

(Слайд 19)

№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.

Используемая литература:

1. Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. — 1456 с.: ил.
2. slovari. yandex.ru
3. urok.1sept.ru/articles/520040
4. Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
5. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. — 528 с.: ил.

Задачи ЕГЭ на сплавы, смеси, растворы.

Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.

. В сосуд, содержащий  литров -процентного водного раствора некоторого вещества, добавили  литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

.

---

. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:

Ответ: .

. Виноград содержит  влаги, а изюм — . Сколько килограммов винограда требуется для получения  килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось  воды, значит, «сухого вещества» было . В изюме  воды и  «сухого вещества». Пусть из кг винограда получилось  кг изюма. Тогда

 от  от 

Составим уравнение:

и найдем .

Ответ: .

---

. Имеется два сплава. Первый сплав содержит  никеля, второй —  никеля. Из этих двух сплавов получили третий сплав массой  кг, содержащий  никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:

Первое уравнение — масса получившегося сплава, второе — масса никеля.

Решая, получим, что .

Ответ: .

---

. Смешав -процентный и -процентный растворы кислоты и добавив  кг чистой воды, получили -процентный раствор кислоты. Если бы вместо  кг воды добавили  кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?

Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.

Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.

Ответ: .

Муниципальное общеобразовательное учреждение

 «Средняя общеобразовательная школа № 2»

Решение текстовых задач: задач на смеси,  сплавы и растворы  при подготовке к ГИА по математике.

( рекомендации учащимся)

                                             Колбасова Л.А., учитель математики высшей категории

1. Теоретические основы решения задач на сплавы и смеси

Решение задач на смеси, сплавы, растворы требует определенной теоретической базы.

Это различные определения, такие как концентрация, процентное содержание и др., а также и всевозможные допущения, например:

1) всё, что мы рассматриваем, считается однородным;

2) все процессы происходят мгновенно;

3) полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;

4) величины, получаемые в результате вычислений, не могут быть со знаком минус.

Существует несколько способов решения задач на слияние растворов. Например, можно воспользоваться расчетной формулой, как это делают на уроках химии. Из области математики можно пользоваться графическим или же алгебраическим методами.

Задачи на смеси и сплавы бывают двух видов:

1. Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
2. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.

В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.

Концентрация вещества — это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.

Масса раствора равна сумме масс всех составляющих.

Алгоритм решения задач на смеси и сплавы:

1. Определить, какое вещество влияет на концентрацию раствора (главное вещество).
2. Следить за весом главного вещества при добавлении других веществ в раствор.
3. Исходя из данных об изменениях состояния главного вещества — сделать выводы.

Как правило, концентрация выражается в процентах.

Процент – это сотая доля числа. Она может выражаться либо в виде десятичной дроби (0,11), либо в виде процента (11%).

Важно знать:

Если мы смешаем 3 литра апельсинового сока и 77 литров воды, то получим 10

10 литров апельсинового нектара (сделаем предположение, что смешивание происходит в автоматическом режиме, а не вручную).

Если мы смешаем 6 литров яблочного сока и 66 литров персикового сока – то получится 12 литров яблочно-персикового сока.

И еще одна очевидность (последняя).

Если мы смешаем 3 литра яблочного сока с 10% мякоти (0,3 л), и 55 литров яблочного сока с 5% мякоти (0,25 л), то получим 88 литров сока с 0,55 л мякоти

(0,3+0,25).

2. Простейшие задачи на смеси и сплавы

Задачи на смеси и сплавы бывают двух основных видов:

1. Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
2. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.

Строго говоря, подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.

Пример 1.

В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)?

Решение:

1. Для начала вычислим, сколько кислоты содержится в 5% растворе. Из 3,8 кг 5% — это кислота, а значит в растворе 0,05 * 3,8=0,19 кг кислоты

2.  Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.

3.  Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – 0,19 кг. Таким образом, концентрация кислоты стала равна 0,19:5=0,038

4. Теперь выразим концентрацию в процентах — 0,038⋅100%=3,8%

Ответ: 3,8

Теперь давай попробуем решить задачу посложнее.

Пример 2.

Смешали 3 кг 5%-го водного раствора щелочи и 7 кг 15%-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.

Решение:

Давай попробуем визуализировать ситуацию. 3 кг 5% водного раствора. Значит воды в этом растворе 95%.

Нарисуем:

А теперь второй раствор: 

После смешивания, вновь получившийся раствор будет весить 3кг + 7 кг = 10 кг. Обозначим количество щелочи в новом растворе за x, а количество воды – (10−x):

Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе –0,05⋅3=0,15 кг щелочи

и 3−0,15=2,85 кг воды,

во втором — 0,15⋅7=1,05 кг щелочи

и 7−1,05=5,95 кг воды:

Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: x=0,15+1,05=1,2 кг кислоты.

Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:

1,2:10=0,12

​Поскольку ответ просят дать в процентах – умножим на 100%

0,12⋅100%=12%.

Ответ: 12.

Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.

3. Алгебраический метод

Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или систем неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.

        Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений. Главное внимание при обучении учащихся способу решения текстовых задач методом составления уравнений должно быть обращено на сознательную отработку этапности решения.

        В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.

1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.

2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.

3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.

4. Изучение полученного решения, критический анализ результата.

При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.  

Этапы решения задачи:

   1. Знакомство с текстом задач и выделение основных компонентов в них. Заполнение таблицы.

Таблица для решения задач имеет следующий вид:

Наименование веществ, растворов, смесей, сплавов	Масса раствора (смеси, сплава)             М	% содержание вещества (доля содержания вещества) m / M * 100%	Масса вещества       m

Или в таком виде:

	1 – й р-р	2 – й  Р-р	Смесь 2 растворов
Масса растворов
Массовая доля раств-го вещества
Масса вещества в растворе

2. Составление уравнения и его решение.

3. Анализ полученных данных, ответ на вопрос задачи.

Рассмотрим примеры решения задач с помощью таблицы.

Пример 4. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?

Решение.

Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в руде) до и после удаления примесей.

	Масса руды, кг	Масса железа, кг	Концентрация (доля железа в руде)
Руда	500	х
Руда после удаления примесей	500-200=300	х-0,125⋅200= x-25

Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна .

Так как масса железа в 200 кг примесей равна 0,125⋅200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна .

По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:

Найдём, что 212,5 кг – масса железа в руде. Найдём остаток железа в руде после удаления примесей: 212,5-25=187,5 (кг).

Ответ: 187,5 кг.

Пример 5. Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Наим-е веществ, растворов, смесей, сплавов	% содержание меди (доля сод-я в-ва)	Масса раствора (смеси, сплава)	Масса вещества
Первый сплав	15%=0,15	хг	0,15х
Второй раствор	65%=0,65	(200 – х)г	0,65(200–х)=130–0,65х
Получившийся р-р	30%=0,3	200 г	2000,3=60

Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы):

                               

Решив это уравнение, получаем х=140. При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять140г, а второго 60г.

Ответ:140г. 60г.

Рассмотрим еще несколько примеров решения задач с помощью таблицы. Как правило обе части уравнения умножают на100, при этом избегают решения уравнения с десятичными дробями.

6.  В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Количество раствора	5 л	+7 л	= 12 л
% содержания растворенного вещества	12 %	0 %	х %
Количество растворенного вещества
	5  12 + 0 = 12х       5  12  = 12х   │ : 12               х = 5                                                                      Ответ: 5.

7.  Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Количество раствора	4 л	+ 6 л	= 10 л
% содержания растворенного вещества	15 %	25 %	х %
	4  15 + 6    = 10х  │ : 10       2  3  +  3  5    =  х                             х = 21                                                           Ответ: 21.

8. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

	виноград	изюм
Количество раствора	х  кг	20  кг
% содержания растворенного вещества	100 – 90 = 10 %	100 – 5 = 95 %
	10х   =   20  95 │ : 10             х = 190                                                                 Ответ: 190.

9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Количество раствора	х  кг	+ (200 – х)  кг	= 200 кг
% содержания растворенного вещества	10 %	30 %	25 %
	10х + 30(200 – х)  = 200  25 │ : 10                                            х + 3(200 – х) = 20  25                                               х + 600 – 3х = 500                                                             — 2х = — 100                                                                  х = 50 (200 – 50) – 50 = 100 Ответ: 100.

10. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Количество раствора	х кг	+ у кг	+ 10 кг	= х + у + 10
% содержания растворенного вещества	30 %	60 %	0 %	36 %
Количество раствора	х кг	+ у кг	+ 10 кг	= х + у + 10
% содержания растворенного вещества	30 %	60 %	50 %	41 %
	х=4 30 – 60 =60 Ответ: 60.

Задания для самостоятельного решения:

1. (Типовые тестовые  задания ЕГЭ 2012  п/р  А.Л.Семенова, И.В.Ященко). Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?

2.  Первый раствор содержит 40% кислоты, а второй —  60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 % раствора, то получился бы 70 % раствор. Сколько литров 60 % раствора кислоты было первоначально?

Список использованной литературы.

1. Кузнецова Л.В. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. — М.: Просвещение, 2010.

2. Прокопенко Н.И. Задачи на смеси и сплавы.- М. :Чистые пруды, 2010 (Библиотечка «Первого сентября». Выпуск 31 )

3. Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.

4.  Малахова Н. А., Орлов В. В. и др. Методика работы с сюжетными задачами: Учебно-методич. пособие. СПб.: Изд-во РГПУ, 1992. 46 с.

5.  Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989

6.  www.mathege.ru

7. www.fipi.ru

8. www. festival.1september.ru

9. http://www.shevkin.ru/

10. http://mat-ege.ru

Работа на тему: «Решение задач на концентрацию, смеси
и сплавы».

        Задачи на
концентрацию, смеси, сплавы.

Задачи на
концентрацию традиционно являются слабым звеном в подготовке школьников и
абитуриентов, кажутся многим из них довольно сложными. Обучение решению этих
задач начинается с 6 класса и продолжается на продолжении всей основной школы.
Однако, в 11 классе эти задачи у большинства вызывают затруднения. При
повторении можно начинать с решения самых простых задач, взятых из учебника
математики для 6 класса. В таких задачах речь обычно идет о растворах
некоторого вещества в другом веществе и об изменении концентрации этого
вещества после  каких-либо манипуляций. При этом водные растворы, смеси, сплавы
играют сходные роли и позволяют лишь несколько разнообразить сюжеты задач без
изменения математического содержания. Ключевой при решении таких задач является
идея отслеживания изменений, происходящих с «чистым» веществом.

В качестве модельной задачи рассмотрим следующую.

 Смешали х литров п- процентного  водного раствора некоторого вещества 
с у литрами  к- процентного водного раствора этого же вещества. Требуется найти
концентрацию получившейся смеси.

 Воспользуемся ключевой идеей: проследим за изменениями, происходящими
с чистым веществом. В первом растворе его было 0,01хп литров, во втором
растворе 0,01ук литров. Значит количество чистого вещества в полученной смеси
будет равно  0,01хп + 0,01ук литров, а всего смеси получится х + у  литров.
Теперь найти искомую концентрацию легко.

( 0,01хп + 0,01ук):
(х + у) ×100= (хп + ук):(х + у). Заметим, что растворы в этой задаче можно было
бы заменить двумя сплавами разной массы и с разным содержанием чистого
вещества. Решение при этом практически не изменится, поменяются лишь единицы
измерения и названия веществ.

Тема : Задачи на проценты и концентрацию.

Цель: формировать умение решать задачи на концентрацию, смеси и сплавы.

1.Устная работа.

Найдите:

а) 50% от
80;         б) 10% от 300           в) 1% от 30     г) 20% от 25          д)25%
от 400

е) 5% от 200;         
ж) 50% от 17             з) 40% от 10   и) 70% от 30          к) 9% от 500.

2.Формирование
умений и навыков.

Задача. Имеются 3 раствора морской соли в воде: первый раствор содержит 10%
соли, второй содержит 15 % соли и третий – 20% соли. Смешали 130 мл первого
раствора, 200 мл второго раствора и 170 мл третьего раствора.

Определите, сколько
процентов составляет морская соль в полученном растворе

Решение:

1)                 
В 130 мл первого раствора содержится 130 × 0,1 = 13
(г) морской соли. В 200 мл второго раствора содержится 200 × 0,15 = 30 (г)
морской соли. В 170 мл третьего раствора содержится 170 × 0,2 = 34 (г) морской
соли.

2)                 
После того, как эти растворы смешали, получили 130
+ 200 + 170 = 500 (мл) нового раствора, который содержит 13 + 30 + 34 = 77 (г)
морской соли.

3)                 
Найдем, сколько процентов составляют 77 (г) морской
соли от 500 мл раствор

.

Задача. Сколько граммов воды надо добавить к 50
г раствора, содержащего 8 % соли, чтобы получить 5 % — ный раствор?

Заметим, что задачи на концентрацию вызывают наибольшие
затруднения у учащихся. Поэтому следует подробнее остановиться на решении
данной задачи, начав не с составления уравнения, а с вопросов, которые помогут
учащимся уяснить условие и осознанно подойти к её решению.

Вопросы учащимся:

1) Сколько граммов соли содержится в имеющемся растворе?

    (50×0,08 = 4 г).

2) Если к имеющемуся раствору добавить воды, изменится ли
массовая составляющая соли? (Нет.)

3) При добавлении воды изменится ли процентное содержание
соли в растворе? (Да.)

4) Если к имеющемуся раствору добавить х г воды,
какова станет масса всего раствора? (50 + х). Сколько граммов соли в нем
будет? (4г).

5) Каково процентное содержание соли в новом растворе?
(5%.)

6) Какую пропорцию, согласно полученным результатам, можно
составить?

4 г соли – 5%

(50 + х) г раствора – 100%.

Имеем уравнение:

5(50 + х) = 400, откуда х = 30.

Ответ: 30г.

Алгоритм.

Поскольку при добавлении к раствору какого-либо вещества
масса другого вещества не изменяется, а меняется его процентное содержание, то
сначала необходимо найти массу изменяющегося вещества.

Затем за х обозначить массу добавляемого вещества и
составить пропорцию, в которой масса неизмененного вещества будет составлять
новое количество процентов, а масса всего раствора 100%.

Задание учащимся.

Решите следующие две задачи по составленному выше
алгоритму.

Задача №1.

Сколько граммов воды надо добавить к 180
г  сиропа, содержащего 25% сахара, чтобы получить 20%-ый сироп?

Решение.

Веществом, которое не меняет своей массы в новом растворе,
является сахар. Поэтому найдем его массу.

180×0,25 = 45 г.

После добавления воды 45
г сахара в новом растворе будут составлять 20 % от всей массы. Пусть х
г воды надо добавить, тогда масса нового раствора составляет (180 + х)
г.

Имеем пропорцию:

45 г сахара – 20%;

(180 + х) г сиропа – 100%.

Из пропорции составим уравнение:

20(180 + х)= 4500, откуда х = 45.

Ответ: 45г.

Задача №2.

Сколько граммов воды надо выпарить из 80
г 6%-ого раствора соли, чтобы получить 10%-й раствор?

Решение.

Масса соли в имеющемся растворе равна 80 × 0,06 = 4,8
г. В новом растворе соль будет составлять 10%.

Пусть х граммов воды нужно выпарить, тогда масса
нового раствора будет равна (80 — х) г.

 Составим пропорцию:

4,8 г соли – 10%;

(80 — х) г раствора – 100%.

Получаем уравнение:

10(80 – х) = 4,8×100, откуда х = 32.

Ответ: 32 г.

Задача №3.

Имеются два сплава. Первый сплав содержит 10% никеля,
второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200
кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы
второго?

Решение.

Пусть масса первого сплава х кг, а масса второго у
кг. Масса третьего сплава х + у и по условию задачи х + у = 200. Первый сплав
содержит 0,1х кг чистого вещества, а второй 0,3у кг. Третий сплав содержит 0,25×200=50
кг. Значит, 0,1х + 0,3у =50. Получили систему из двух линейных уравнений.
Решением системы является пара чисел х=50 и у=150. Итак, масса первого сплава
на 150 – 50 =100 кг меньше.

Ответ: 100.

Задача №4.

Первый сплав содержит 10% меди, второй – 40 % меди. Масса
второго сплава больше массы первого на 3
кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите
массу третьего сплава. Ответ дайте в килограммах.

Решение.

Пусть масса первого сплава х кг, тогда масса второго сплава
( х + 3 )кг. Масса третьего сплава х + х + 3 = 2х +3
кг. Масса чистого вещества в первом сплаве 0,1х кг, во втором – 0,4×( х+3),
значит всего чистого вещества 0,1х + 0,4(х+3). Так как третий сплав содержит
30% меди, т.е. 0,3( 2х +3), то имеем уравнение 0,3( 2х +3)= 0,1 + 0,4( х+3),
откуда х = 3. Масса третьего сплава  равна 2×3 +3 = 9
кг.

Ответ: 9.

Задача №5.

Виноград содержит 91% влаги, а изюм – 7%. Сколько
килограммов винограда требуется для получения 21 килограмма изюма?

Решение.

Используем ключевую идею: будем следить за массой
«чистого», т.е. в данном случае «сухого» вещества в винограде и изюме. Виноград
содержит чистого вещества 100% — 91% = 9%, а изюм содержит чистого вещества
100% — 7% =  93%. Пусть для получения 21 килограмма изюма требуется х кг
винограда. Из условия следует, что масса «сухого» вещества в х кг
винограда равна 0,09х кг. Поскольку эта масса равна массе «сухого»вещества в 21
килограмме изюма, то по условию задачи можно составить уравнение

0,09х=0,93×21,

откуда

9х = 93×21,

т.е. х = 217
кг.

Ответ: 217 кг.

Задача для самостоятельного решения.

Виноград содержит 90% влаги, а изюм – 5%. Сколько
килограммов винограда требуется для получения 20 килограмма изюма?

Ответ:190кг.

Задача №6.

В сосуд, содержащий 5
литров 12-процентного водного раствора некоторого вещества, добавили 7
литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение.

 В 5 литрах раствора содержится 0,12×5 = 0,6
л чистого вещества. Масса нового раствора 12
литров, а чистого вещества в нем по прежнему 0,6
л. Значит концентрация нового раствора равна 0,6 : 12×100% =5%.

Ответ: 5.

Задача №7.

Смешали некоторое количество 15-процентного раствора
некоторого вещества с таким же количеством 19- процентного раствора этого же
вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

  Пусть масса первого раствора х г, он содержит 0,15х г
чистого вещества. Масса второго раствора тоже х г, он содержит 0,19х г чистого
вещества. Масса нового раствора равна х + х = 2х г и он содержит 0,15х + 0,19х
= 0,34х г чистого вещества. Тогда концентрация нового раствора равна ( 0,34х) :
(2х)×100% = 17%.

Ответ: 17.

Задача  для самостоятельного решения.

Смешали 4 литра 15-процентного раствора некоторого вещества
с 6 литрами 25-процентного водного раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?

Ответ: 21.

Итоги урока.

Вопросы учащимся:

— Как найти процент от величины?

— Как найти величину по ее проценту?

— Как найти, сколько процентов одна величина составляет от
другой величины?

— Каков алгоритм решения задач на концентрацию, в которых к
имеющемуся раствору      добавляют одно из составляющих его веществ?

— По какому плану решаются задачи на смешивание нескольких
растворов?

ЛИТЕРАТУРА

1.Математика. 6 класс: поурочные планы по учебнику
Г.В.Дорофеева, С.Б.Суворовой, И.Ф.Шарыгина. Часть 1/авт.-сост. Т.Ю.Дюмина. –
Волгоград: Учитель,2007.

2.Алгебра. 7 класс: поурочные планы по учебнику под
редакцией Г.В.Дорофеева / авт.-сост. М.Ф. Калинина. – Волгоград: Учитель,2008.

3.Алгебра. 8 класс: поурочные планы по учебнику под
редакцией Г. .В. Дорофеева / авт. – сост. Т. Ю. Дюмина. – Волгоград:
Учитель,2008.

4.Шестаков С.А., Гущин Д.Д. ЕГЭ 2011. Математика. Задача
В12. Задачи на составление уравнений. Рабочая тетрадь / Под ред. А.Л.Семенова и
И.В.Ященко. – М.: МЦНМО, 2011.

Задачи на смеси и сплавы — подробнее

Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.

То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.

Обычно концентрация измеряется в процентах.

Что такое процент?

Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.

Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).

Почему?

Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).

Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?

Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.

Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.

Более подробно о процентах – в темах  «Дроби, и действия с дробями»и «Проценты».

Поехали дальше.

Масса раствора, смеси или сплава равна сумма масс всех составляющих.

Логично, правда?

Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.

И еще одна очевидность:

При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.

А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.

Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.

Когда мы их смешаем, чему будет равна масса нового раствора?

( displaystyle 10+14=24) кг.

А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.

Перейдем к задачам.

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)

В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.

Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).

Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.

Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.

Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).

ЕГЭ №17 Экономическая задача. Вклады

Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!

Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.

По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.

Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!

На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.