И
ПЛОТНОСТИ СПЛАВОВ
Концентрация
— величина, определяющая содержание
компонента в смеси, растворе, сплаве.
Способы выражения концентрации различные.
В
физике концентрация – n
— это количество частиц в единице объема
; [c]
= M-3
в СИ.
По
этой формуле определяют число атомов
или молекул в единице объема, а также
концентрацию электронов, дырок и др.
Долевая
(относительная) концентрация Сm
по
массе
есть отношение массы компонента mi
к
общей массе смеси
m
.
По
этой формуле чаще всего определяют
концентрацию компонента (по массе) в
сплавах. Например, в бинарном сплаве
А10В90
содержится 10масс.% компонента А и 90масс.%
компонента В.
Атомная
(молекулярная) долевая концентрация
Сат
–
это отношение содержащегося в смеси
числа атомов (молекул) Nx
компонента
к числу атомов (молекул) всех компонентов
N
.
Мольная
долевая концентрация С
— это отношение содержащегося в смеси
числа молей х
одного
из компонентов к общему числу
молей вещества
С
х/.
Концентрации Сm
,Сат
,С
выражаются в виде дроби, либо в процентах.
Относительная концентрация Сат
чаще
всего используется для нахождения
концентрации вакансий, либо атомов
примесей. В этом случае под Nx
подразумевают
число вакансий, либо инородных атомов,
а под N–
число узлов кристаллической решетки,
либо общее число позиций, которые могут
быть заняты атомами примесей (обычно
их также приравнивают к числу узлов в
кристаллической решетке).
Молярная
концентрация С
удобна для определения концентрации
компонента в смеси газов, либо в растворе
жидкости.
Моль
раствора
М
–
количество раствора, при котором число
молей каждого компонента равно его
молярной доле
,
где
—
молярная массаi-гокомпонента.
Молярность
– число молей вещества в 1 литре раствора
(моль/л или моль/м3)
.
Мольность
– число молей вещества в 1 кг растворителя
(моль/кг)
.
Титр
– масса вещества 1 мл раствора
.
Объемная
концентрация
—отношение
объема Vx,
занимаемого компонентом к общему объему
V
системы
.
Концентрация
компонента по плотности
—
отношение массы компонентаm
к объему системы V
,
.
Согласно
системе СИ к концентрации относят
только массовую Сm
и
молярную С
концентрации. Все остальные характеристики
содержания компонента не являются
концентрациями.
При
изготовлении сплавов часто возникают
практические задачи по определению
плотности
сплавов,
атомной
Са
,
массовой Сm
и
молярной С
концентраций сплавов, а также молярной
массы сплава М.
Приведем наиболее распространенные
методы вычисления этих параметров для
бинарных и тройных сплавов.
Бинарные сплавы
Задача
№1.
Определить
относительное содержание компонентов
и
по массе, если известны плотности
компонентови смеси
,
,
,
,
,
,
,
из
этой системы находим
или
, откуда
,
следовательно,
.
Тогда
.
(23.1)
Аналогично ,
(23.2)
или , (или
100%).
Например,
для сплава олово-свинец с плотностью
=102/см3
имеем
.
Задача
№ 2.
Найти
плотность
сплава, если известны массыm1,
m2
и
плотности
и
компонентов
,
,
,
,
,

. (23.3)
Например,
для сплава олова и свинца при
и
имеем
.
Задача
№ 3.
Найти
плотность
для сплава при заданных концентрациях
и
компонентов и их плотностях
и
.

.
(23.4)
Например,
для сплава олова с свинцом при
получим
.
Задача
№ 4.
Найти
массу m2
второго
компонента в сплаве при известной массе
m1
первого компонента и его массовой
концентрации
.

(23.5)
Задача
№ 5.
Найти
атомный процент
,
компонентов
сплава, если известны их массы и
молекулярные массы.
;


(23.7)
Задача
№ 6.
Найти
молярный процент
компонентов сплава, если известны их
молярные массыМ1,
М2
и
массы компонентов m1
и m2..
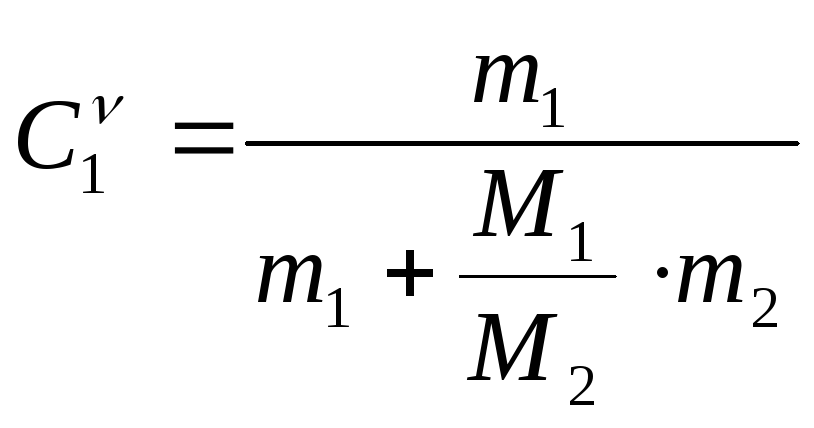

(23.9)
Задача
№ 7.
При
известных атомных концентрациях
компонентов
и
найти массовые концентрации
и
.


(23.11)
Задача
№ 8.
При
известных массовых концентрациях
и
компонентов найти атомные концентрации
компонентов.

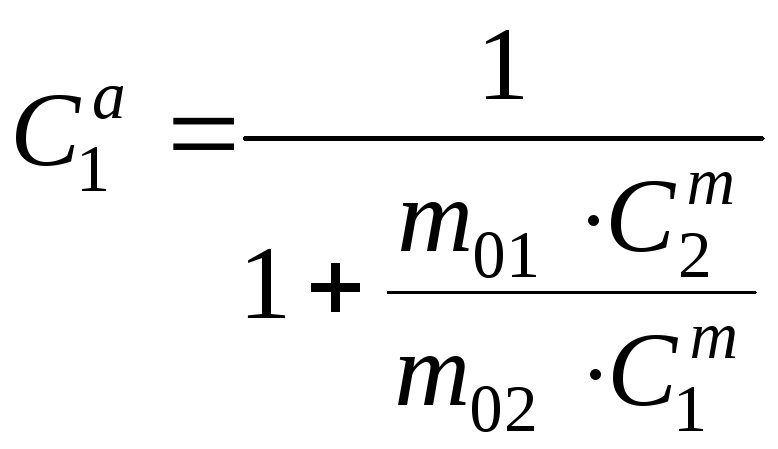

(23.13)
Задача
№ 9.
По
массовым концентрациям
и
найти молярные концентрации
и
.

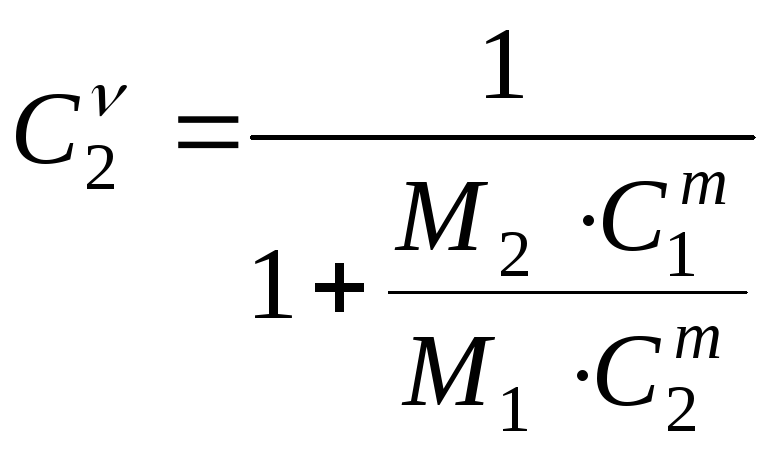
(23.15)
Задача
№ 10.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
— масса раствора = масса воды + масса соли;
— масса сплава равна сумме масс металлов, входящих в этот сплав;
— масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе — это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс — масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси — это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв — масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве — это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв — масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М — масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% — 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Задачи ЕГЭ на сплавы, смеси, растворы.
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий
литров
-процентного водного раствора некоторого вещества, добавили
литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .
Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
.
. Смешали некоторое количество
-процентного раствора некоторого вещества с таким же количеством
-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна . Масса второго — тоже
. В результате получили раствор массой
. Рисуем картинку.
Получаем:
Ответ: .
. Виноград содержит
влаги, а изюм —
. Сколько килограммов винограда требуется для получения
килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было
. В изюме
воды и
«сухого вещества». Пусть из
кг винограда получилось
кг изюма. Тогда
от
от
Составим уравнение:
и найдем .
Ответ: .
. Имеется два сплава. Первый сплав содержит
никеля, второй —
никеля. Из этих двух сплавов получили третий сплав массой
кг, содержащий
никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .
Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что .
Ответ: .
. Смешав
-процентный и
-процентный растворы кислоты и добавив
кг чистой воды, получили
-процентный раствор кислоты. Если бы вместо
кг воды добавили
кг
-процентного раствора той же кислоты, то получили бы
-процентный раствор кислоты. Сколько килограммов
-процентного раствора использовали для получения смеси?
Пусть масса первого раствора , масса второго равна
. Масса получившегося раствора равна
. Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
Ответ: .
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на сплавы, смеси, растворы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Решение задач на концентрацию, растворы, сплавы.
§1. Элементы текстовых задач на смеси, сплавы, растворы. Формула
Все текстовые задачи на смеси, сплавы и растворы содержат в себе три основных элемента.
Это ЦЕЛОЕ – масса смеси, сплава или раствора, выраженная в граммах, литрах или других мерах веса и объёма;
ЧАСТЬ – масса определённого вещества в составе смеси, сплава или раствора, выраженная в граммах, литрах или других мерах веса и объёма;
ДОЛЯ – доля вещества в смеси, сплаве или растворе, выраженная в процентах или, чаще, дробным числом без наименования.
Все три элемента взаимосвязаны между собой формулой
Для более быстрого запоминания этой формулы её удобно записать в треугольник, разбитый на три части. В верхней части запишем ЧАСТЬ, а в двух нижних частях – ЦЕЛОЕ и ДОЛЯ. При этом горизонтальная черта означает деление, а вертикальная – умножение.
Согласно формуле, для того,
— чтобы найти ЧАСТЬ, надо ЦЕЛОЕ умножить на ДОЛЮ;
— чтобы найти ЦЕЛОЕ, надо ЧАСТЬ разделить на ДОЛЮ;
— чтобы найти ДОЛЮ, надо ЧАСТЬ разделить на ЦЕЛОЕ.
§2. Решение простейших текстовых задач на смеси, сплавы, растворы
Рассмотрим простейшие задачи на применение этой формулы.
ЗАДАЧА 1. Сколько граммов поваренной соли содержится в 200граммах 9%-ного солёного раствора?
РЕШЕНИЕ.
В этой задаче ЦЕЛОЕ – это масса солёного раствора, 9% = 0,09 – это ДОЛЯ соли в растворе, ЧАСТЬ – это масса соли в растворе. Таким образом, в задаче надо найти часть. Для этого надо ЦЕЛОЕ 200г умножить на ДОЛЮ 0,09. Получили, что 18граммов поваренной соли содержится в 200граммах 9%-ного солёного раствора.
ЗАДАЧА 2. Определить концентрацию раствора 50граммов сахара в 450граммах воды.
РЕШЕНИЕ.
В этой задаче ЦЕЛОЕ – это масса сладкого раствора, равная 450г + 50г =500г, ЧАСТЬ – это масса сахара в растворе 50г. Таким образом, в задаче надо найти ДОЛЮ, которая и является концентрацией сахара в растворе. Для этого надо ЧАСТЬ 50г разделить на ЦЕЛОЕ 500г. Получили, что концентрация раствора равна 0,1 или 10%.
§3. Решение более сложных текстовых задач на смеси, сплавы, растворы
В жизни чаще встречаются более сложные задачи, в которых взаимодействуют несколько смесей, сплавов и растворов. Все такие задачи условно можно разбить на группы:
-задачи на понижение концентрации;
— задачи на высушивание;
— задачи на смешивание растворов разных концентраций;
— задачи на переливание;
-задачи на повышение концентрации.
Рассмотрим примеры решения таких задач.
ЗАДАЧА. Сколько килограммов воды надо добавить к 60г 16%-ной соляной кислоты, чтобы получить 10%-ный раствор этой кислоты?
РЕШЕНИЕ.
1 арифметический способ.
Так как к соляной кислоте добавляют воду, не содержащую кислоту, то увеличившаяся масса раствора будет обратно пропорциональна концентрации, то есть с увеличением массы раствора концентрация будет уменьшаться во столько же раз. Значит, масса нового раствора относится к массе соляной кислоты 60г так же, как концентрация 16% относится к концентрации 10%. Из пропорции несложно вычислить массу нового раствора из числового выражения произведение 60-ти и 16-ти, делённое на 10. Масса чистой воды равна разности 96-ти и 60-ти, то есть 36г или 0,036кг.
Мы решили задачу арифметическим способом и ответили на главный вопрос задачи: 0,036кг воды надо добавить в 16%-ную соляную кислоту.
2 алгебраический способ.
Запишем условия задачи в виде таблицы – схемы. Смоделируем данные жидкостей в прямоугольники. В первом прямоугольнике запишем массу соляной кислоты 60г, над ним – концентрацию 16% = 0,16, под ним – массу кислоты в растворе, равную 0,16 умноженной на 60г. Далее поставим знак «плюс», так как по условию к раствору добавляют воду, с отмеченной массой воды mг. В результате должен получиться 10% — ный раствор массой (60 + m)г. Значит, изобразим его в виде прямоугольника с записью 60 + m внутри его, над ним запишем 10% = 0,1, под ним – 0,1(m + 60). Из выражений под прямоугольниками получаем уравнение 0,1 (60 + m) = 0,16∙ 60. Решая его, находим значение переменной m равной 36г.
ЗАДАЧА. Имеется сплав меди с оловом массой 12кг, содержащий 45% меди. Сколько чистого олова надо добавить, чтобы получить сплав, в котором содержится 40% меди?
РЕШЕНИЕ:
1 схематический способ.
Запишем в прямоугольнике концентрацию меди в первом сплаве 45%, ниже в другом прямоугольнике запишем концентрацию меди 0% второго куска, содержащего только олово. В центре второго столбца в прямоугольнике запишем концентрацию нового сплава с концентрацией меди 40%. В третий столбик, применяя правило «крестика», сверху вниз запишем результаты разности 40 – 0% и разности 45 – 40%. Получили числа 40% и 5%. Разделим их на 5 и результаты запишем в 4-й столбик в соответствующих строках. Таким образом, для получения 40% сплава меди с оловом, надо взять 8 частей 45%-ного сплава и 1 часть чистого олова. По условию задачи 45% -й сплав меди с оловом имеет массу 12кг, что составляет 8 частей. Значит, на одну часть приходится 12кг делённое на 8, то есть 1,5кг. Следовательно, чистого олова надо взять 1,5кг. Мы решили задачу схематическим способом.
2 геометрический способ. Смоделируем 45%-ный сплав меди с оловом в виде прямоугольника условной длиной в 12кг и условной шириной 45%. На него наложим прямоугольник условной длиной (12 + m)кг и условной шириной 40%. Оба прямоугольника должны быть равновелики, так как содержат одинаковые массы меди. Следовательно, площади их частей S1 = 5∙12 и S2= 40m равны между собой. Значит, решая уравнение 40m = 5∙12, имеем, что m = 1,5. Таким образом, с помощью геометрического способа мы ответили на главный вопрос задачи 1,5 кг чистого олова надо добавить для получения 40% -ного содержания меди в сплаве.
ЗАДАЧА. Индийский чай дороже грузинского на 25%. В каких пропорциях нужно смешать индийский чай с грузинским, чтобы получить чай, который дороже грузинского на 20%.
РЕШЕНИЕ:
Цена индийского чая дороже на 25%, значит, составляет 125% от цены грузинского чая, следовательно, доля цены индийского чая равна 1,25, а доля цены грузинского чая равна 1-ой единице. Решим задачу схематическим способом по правилу «крестика». В первом столбике друг под другом запишем доли цен грузинского и индийского чая соответственно, то есть 1 и 1,25. Во втором столбике в центре поместим долю смеси, которая дороже грузинского чая на 20%, то есть 120% равно 1,2. В третьем столбике «крестиком» друг под другом запишем разности 1,25 – 1,2 = 0,05 и 1,2 – 1 = 0,2. Чтобы избавиться от дробных чисел, домножим оба результата третьего столбика на 20. Получили числа 1 и 4, которые показывают доли грузинского и индийского чая соответственно для получения нужной смеси. Таким образом, мы ответили на главный вопрос задачи индийский и грузинский чай надо взять в отношении 4 к 1 соответственно.
§4. Решение текстовых задач на смеси, сплавы, растворы с помощью уравнений
Рассмотрим текстовые задачи на смеси, сплавы и растворы, которые решаются с помощью линейных уравнений и с помощью систем линейных уравнений.
ЗАДАЧА: Пчёлы перерабатывают цветочный нектар в мёд, освобождая его от воды. Нектар обычно содержит 84% воды, а полученный из него мёд – 20%. Сколько килограммов нектара приходится перерабатывать пчёлам, чтобы получить 2кг мёда?
РЕШЕНИЕ:
В процессе переработки нектара в мёд неизменном остаётся масса сухого вещества этих продуктов. Поэтому найдём долю сухого вещества в нектаре и в мёде. Она будет равна
100% — 84% , то есть 16-ти% или 0,16 в нектаре и 100% — 20%, то есть 80-ти % или 0,8 в мёде. Пусть х кг нектара надо переработать пчёлам, тогда сухого вещества в нектаре будет 0,16х кг, а в мёде 0,8 умноженное на 2кг, то есть 1,6кг. Решая простейшее уравнение 0,16х =1,6, получаем х = 10. Таким образом, мы ответили на главный вопрос задачи 10кг нектара надо переработать пчёлам для получения 2кг мёда.
ЗАДАЧА: Смешали два сорта творога. Жирный творог массой 400г содержит 20% жира, а нежирный творог массой 500г содержит 2% жира. Определить процент получившегося творога.
РЕШЕНИЕ:
Решим задачу комбинированным схематическим и алгебраическим способом.
В первый столбик выпишем данные жирности творога в порядке возрастания. Обозначим процент получившегося творога буквой р% и запишем в центре второго столбика. Тогда в третьем столбике друг под другом по правилу «крестика» запишем разности 20-р и р-2. Эти выражения показывают части жирного и нежирного творога, взятые для получения р%-ной жирности. Таким образом, имеем 20-р частей приходится на 500г нежирного творога и р-2 частей приходится на 400г жирного творога.
Из пропорции (20 – р) относится к (р – 2) так же как 500 относится к 400, получаем простое уравнение 400(20 – р) = 500(р – 2). Решив его, имеем р = 10.
Мы ответили на главный вопрос задачи, получится 10% -ный творог из 400г жирного и 500г нежирного творога.
§5. Решение текстовых задач на смеси, сплавы, растворы с помощью систем уравнений
ЗАДАЧА: Имеются два сосуда, содержащие 30кг и 35кг раствора кислоты различной концентрации. Если смешать оба раствора, то получится раствор, содержащий 46% кислоты. Если смешать равные массы этих растворов, то получится раствор, содержащий 47% кислоты. Какова концентрация данных растворов?
РЕШЕНИЕ:
Решим задачу алгебраическим способом, приняв неизвестные концентрации за х — долю кислоты в 30кг и у – долю кислоты в 35кг раствора. Запишем условия задачи в виде таблицы – схемы. Из первой части задачи в двух прямоугольниках, разделённых знаком «плюс» выпишем массы растворов 30кг и 35кг, над ними запишем их концентрации х и у соответственно, а под прямоугольниками запишем выраженные массы чистой кислоты в каждом растворе 30х и 35у соответственно. Затем поставим знак равно и в третьем прямоугольнике запишем массу нового раствора 30 + 35 = 65кг. Над прямоугольником поставим концентрацию нового раствора, выраженную в доле, то есть 46% равную 0,46, а под прямоугольником — массу чистой кислоты 0,46 ∙ 65кг равную 29,9кг.
Получили уравнение с двумя переменными 30х + 35у = 29,9.
Из второй части задачи в двух прямоугольниках, разделённых знаком «плюс» выпишем массы растворов m кг и m кг, так как по условию они равны. Над прямоугольниками запишем их концентрации х и у соответственно, а под прямоугольниками запишем выраженные массы чистой кислоты в каждом растворе mх кг и mу кг соответственно. Затем поставим знак равно и в третьем прямоугольнике запишем массу нового раствора m + m = 2m кг. Над прямоугольником поставим концентрацию нового раствора, выраженную в доле, то есть 47% равную 0,47, а под прямоугольником — массу чистой кислоты 0,47 умноженное на 2m кг равную 0,94m кг.
Получили уравнение mх + mу = 0,94m. Разделив обе части уравнения на m, получаем уравнение с двумя переменными х + у = 0,94.
Решая систему двух линейных уравнений с двумя переменными, имеем х = 0,6 = 60% и у = 0,34 = 34%. Таким образом, 30-ти кг раствор имеет концентрацию 60%, 35-ти кг раствор – 34% кислоты.






