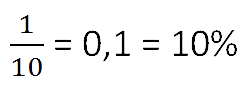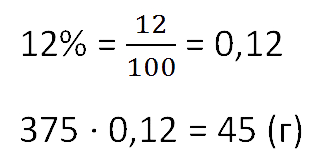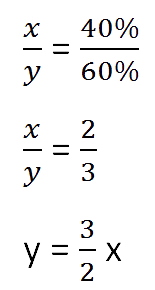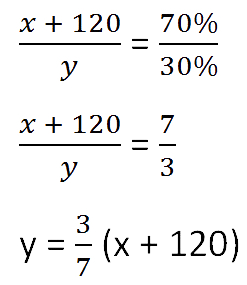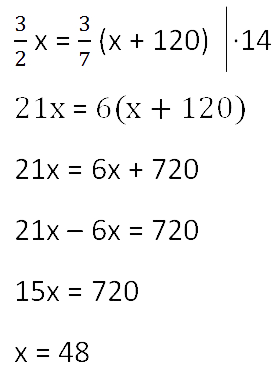Как найти концентрацию вещества по математике

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

• повторить понятия проценты, отношения;
• закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
• показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

• показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
• воспитание у учащихся интереса к предмету.

Развивающие

• развивать наблюдательность, логическое мышление учащихся;
• развивать жизненную смекалку и интуицию.

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.

План урока:

1. Мотивационный момент (1 минута).
2. Подготовка учащихся к сознательному усвоению нового материала (5 минут).
3. Изучение нового материала (12 минут).
4. Решение задач на отработку формул (3 мин).
5. Физминутка (1 минута).
6. Первичное закрепление нового материала (15минут).
7. Рефлексия (1 минута).
8. Подведение итогов. Домашнее задание (2 минуты).

Ход урока

I. Мотивационный момент.

Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.

II. Подготовка к сознательному усвоению нового материала.

(Слайд 2)

1. Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
2. Указать в виде процентов: 0,7; 0,04; 1,3.
3. Найти 15% от числа 60.
4. Найти число, 15% которого равны 30.
5. Из 25 семян взошло 24 семени. Найдите процент всхожести.
6. Итак, известные нам отношения: (Слайд 3)

Всхожесть = ; .

Значения данных отношений мы представляли в виде процентов.

III. Изучение нового материала.

Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?

В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].

Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].

Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)

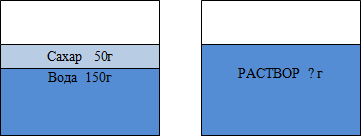
Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

50+150=200 (г) – масса общая. (Слайд 5)

Раствор тщательно перемешиваем.

Найдите процентное содержание сахара в растворе.

50 : 200=1: 4 = 0,25;

0,25=25%

25% – процентное содержание сахара в данном растворе.

Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)

Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).

Концентрация = , т.е. К=.

Как по этой формуле найти М_ч.в? М_общ?

М_ч.в. = М_общ · К

М_общ = Мч.в: К

(Слайд 7)

IV. Решение задач на отработку формул:

(Слайд

1. В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
2. 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
3. Какова масса раствора, в котором 150 г сахара составляют 25%.

Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)

Рис.1.

Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».

Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.

V. Физминутка.

(Слайд 11)

Следите глазами за движениями черепашек.

VI. Первичное закрепление нового материала.

Решим несколько задач на «концентрацию».

(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.

Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)

Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.

Решение:

1. Какова масса раствора в первой банке?
   480+120 = 600 (г)

2. Какова концентрация сахара в растворе первой банки?
   120:600 = 0,2; 0,2=20%

3. Какова масса раствора во второй банке?
   840+160 = 1000(г)

4. Какова концентрация сахара в растворе второй банки?
   160:1000 = 0,16; 0,16=16%

5. В какой банке вода слаще?
   20% > 16%

Ответ: в первой банке вода слаще.

Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)

Решение:

80% – это процентное содержание соли в 200г раствора (концентрация 0,8)

1. Сколько г соли в этом растворе?
   0,8 ·200=160(г)

20% – это содержание соли в 700 г раствора (концентрация соли 0,2)

1. Сколько г соли во втором растворе?
   0,2·700=140 (г)
2. Сколько г соли в полученном растворе?
   160+140=300 (г)

Ответ: 300 г.

Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)

Решение:

50% – процентное содержание соли в 200 г растворе (концентрация 0,5).

1. Сколько г соли в этом растворе?
   0,5·200=100 (г)
   Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25)

2. Какова масса второго раствора?
   150:0,25= 600 (г)
   Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора.

3. Какова масса соли в двух растворах?
   100+150=250 (г)

4. Какова масса нового раствора?
   200+600 =800 (г)

5. Какова концентрация соли в новом растворе?
   250:800=0,3125; 0,3125 = 31,25%

Ответ: 31,25%.

Задача для самостоятельного решения (дома).

Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]

Решение:

1. Сколько кг соли в морской воде?
   0,05·30=1,5 (кг)
   Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015.

2. Какова масса нового раствора (с добавлением пресной воды)?
   1,5: 0,015= 100 (кг)

3. Сколько пресной воды нужно добавить?
   100 – 30 = 70 (кг)

Ответ: 70 кг.

VII. Этап рефлексии.

(Слайд 18)

Ответ на листочке:

• Сегодня я узнал….
• У меня получилось…
• Было трудно….
• Было интересно….
• Теперь я умею…

VIII. Итог урока. Домашнее задание.

(Слайд 19)

№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.

Используемая литература:

1. Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. — 1456 с.: ил.
2. slovari. yandex.ru
3. urok.1sept.ru/articles/520040
4. Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
5. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. — 528 с.: ил.

Задачи ЕГЭ на сплавы, смеси, растворы.

Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.

. В сосуд, содержащий  литров -процентного водного раствора некоторого вещества, добавили  литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

.

---

. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:

Ответ: .

. Виноград содержит  влаги, а изюм — . Сколько килограммов винограда требуется для получения  килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось  воды, значит, «сухого вещества» было . В изюме  воды и  «сухого вещества». Пусть из кг винограда получилось  кг изюма. Тогда

 от  от 

Составим уравнение:

и найдем .

Ответ: .

---

. Имеется два сплава. Первый сплав содержит  никеля, второй —  никеля. Из этих двух сплавов получили третий сплав массой  кг, содержащий  никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:

Первое уравнение — масса получившегося сплава, второе — масса никеля.

Решая, получим, что .

Ответ: .

---

. Смешав -процентный и -процентный растворы кислоты и добавив  кг чистой воды, получили -процентный раствор кислоты. Если бы вместо  кг воды добавили  кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?

Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.

Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.

Ответ: .

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.

• 9%-я концентрация раствора соли — это 9 грамм соли в
  100 граммах раствора.

Разбор примера

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.

Ответ: 10% — концентрация раствора.

Разбор примера

Теперь решим обратную задачу.

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.

Сложная задача на растворы

В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?

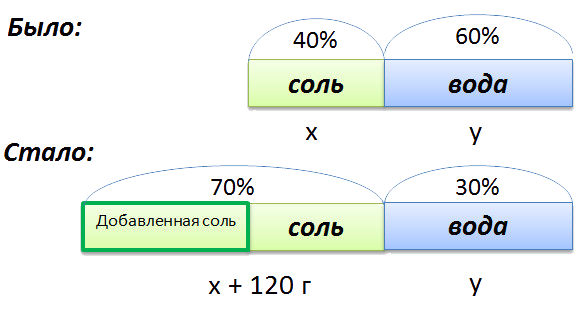
Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет

100% − 40%= 60%

Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.

Этой величиной является масса воды в растворе «y».

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г — масса соли в новом растворе
• (100% − 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.

Ответ: 48 г — масса соли в первоначальном растворе.

---

Ваши комментарии

Оставить комментарий:

---

Задачи на концентрацию

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Задачи на концентрацию являются основными задачами в школьном курсе химии, но различные способы решения таких задач можно рассматривать на уроках математики ещё с шестого класса, используя арифметический способ и понятие процента и десятичной дроби. Затем продолжить в седьмом классе изучив понятие пропорции, а так же умение решать задачи алгебраическим способом, то есть уравнением. И, наконец, в восьмом классе рассмотреть возможность решения таких задач с помощью систем уравнений.

При подготовке ГИА необходимо вспомнить и систематизировать типы и способы решения таких задач.

Арифметический способ

При изучении темы «Проценты» в 6 классе решение задач на концентрацию считаются задачами повышенной сложности и могут быть предложены особо подготовленным учащимся.

Задача 1. Имеется 735 г шестнадцатипроцентного раствора йода в спирте. Нужно получить десятипроцентный раствор йода. Сколько граммов спирта нужно долить для этого к уже имеющемуся раствору?

Решение:

1) Найдем, сколько чистого йода содержится в растворе.

735 · 0,16 = 117,6 (г).

2) В новом растворе йода останется такое же количество, но он будет составлять уже 10 % раствора.

Если 117,6 г – это 10 %, то весь раствор имеет массу 117,6 · 10 = 1176 (г).

3) Найдем, сколько спирта нужно долить для получения нового раствора.

1176 – 735 = 441 (г).

О т в е т: 441 г.

Алгоритм:

Найти массу чистого вещества в растворе. Эта масса будет сохраняться в новом растворе.

Найти массу нового раствора в соответствии с процентным содержанием в нем вещества.

Найти разность масс нового и старого растворов. [3]

Решение с помощью пропорции

Познакомившись с понятием пропорции в 7 классе, подобные задачи можно решать используя это понятие.

Задача 2. К 200 г 30 %-ного раствора соли долили 50 г воды. Какова концентрация полученного раствора?

Р е ш е н и е.

Составим соответствующую пропорцию, приняв за х массу соли в растворе:

200 г – 100 %

х г – 30 % , тогда х = = 60 г соли.

Масса нового раствора 200 + 50 = 250 г, но масса соли в нём не изменилась, т. е. получим

250 г – 100 %

60 г – х % , тогда х = = 24 % концентрация полученного раствора.

О т в е т: получили 24 %-ный раствор.

Задача 3. Смешали 12 л 15 %-ного раствора соляной кислоты и 10 л 10 %-ного раствора. Каково процентное содержание кислоты в полученном растворе? Ответ округлить до 0,1 %.

Р е ш е н и е

С помощью пропорций найдём массу кислоты в каждом растворе:

12 л – 100 %

х л – 15 %, х = = 1,8 л кислоты в первом растворе и

10 л – 100 %

х л – 10 %, х = = 1 л кислоты во втором растворе, всего 2,8 литра.

Так как масса кислоты не меняется, а общая масса растворов 12 + 10 = 22 л, то получим

22 л – 100 %

2,8л – х %, х = ≈ 12,7 %.

О т в е т: 12,7 % кислоты.[4]

Алгебраический способ

Задача 4. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 %-ный раствор?

Начнём решение этой задачи не с составления уравнения, а с вопросов, которые помогут уяснить условие и осознанно подойти к ее решению, используем так же при этом понятие пропорции.

Вопросы:

1) Сколько граммов соли содержится в имеющемся растворе?

(50 · 0,08 = 4 г.)

2) Если к имеющемуся раствору добавить воды, изменится ли массовая составляющая соли? (Нет.)

3) При добавлении воды изменится ли процентное содержание соли в растворе? (Да.)

4) Если к имеющемуся раствору добавить х г воды, какова станет масса всего раствора? (50 + х). Сколько граммов соли в нем будет? (4 г.)

5) Каково процентное содержание соли в новом растворе? (5 %.)

6) Какую пропорцию, согласно полученным результатам, можно составить?

4 г соли – 5 %

(50 + х) г раствора – 100 %.

Имеем уравнение:

5 (50 + х) = 400, откуда х = 30.

О т в е т: 30 г.

Алгоритм.

Поскольку при добавлении к раствору какого-либо вещества масса другого вещества не изменяется, а меняется его процентное содержание, то сначала необходимо найти массу неизменяющегося вещества.

Затем за х обозначить массу добавляемого вещества и составить пропорцию, в которой масса неизменного вещества будет составлять новое количество процентов, а масса всего раствора 100 %. [2]

Решим данные задачи по составленному выше алгоритму.

Задача 5. Сколько граммов воды нужно выпарить из 80 г 6 %-ного раствора соли, чтобы получить раствор, содержащий 10 % соли?

Решение:

Масса соли в имеющемся растворе равна 80 · 0,06 = 4,8 г. В новом растворе соль будет составлять 10 %.

Пусть х г воды нужно выпарить, тогда масса нового раствора будет равна (80 – х) г.

Составим пропорцию:

4,8 г соли – 10 %;

(80 – х) г раствора – 100 %.

Получаем уравнение:

10 (80 – х) = 4,8 · 100, откуда х = 32.

Ответ: 32 г.

Задача 6. Сколько граммов 75%-ного раствора кислоты надо добавить к 30 г 15%-ного раствора этой же кислоты, чтобы получить 50%-ный раствор?

х г — количество 75%-ного раствора кислоты, которое надо добавить;

(30 + х) г — масса получившегося 50%-ного раствора кис­лоты;

0,75х г — количество кислоты в х г 75%-ного раствора;

0,15 ∙ 30 г — количество кислоты в 30 г 15%-ного раствора;

0,5(30 + х) г — количество кислоты в 50%-ном растворе. Имеем уравнение:

кол-во кислоты кол-во кислоты кол-во кислоты

в 75%-ном + в 15%-ном = в 50%-ном

растворе растворе растворе

0,75х + 0,15 ∙ 30 = 0,5(30 + х)

0,75х + 0,15 ∙ 30 = 0,5(30 + х), откуда х = 46 г.

Ответ: 46 грамм.[1]

Решение задач с помощью систем уравнений

Задачи такого типа последние годы встречаются на Основном Государственном Экзамене и Едином Государственном Экзамене.

Задача 7. В колбу налили некоторое количество 60% -ного раствора со­ли и некоторое количество 80%-ного раствора этой же соли. Получили 35 мл раствора, содержащего 72% соли. Сколько миллилитров каждого раствора налили в колбу? Решим зада­чу, используя следующий план:

Обозначим буквами количество 60%-ного и 80%-ного раст­воров соли, налитых в колбу.

Запишем уравнение, связывающее эти две величины и об­щее количество раствора.

Определим количество соли в получившемся растворе.

Запишем уравнение, связывающее количество соли в 60%-ном, 80%-ном и получившемся растворах.

Составим систему и решим ее.

1) Пусть взяли х мл 60 %-ного раствора соли и у мл 80 %-ного раствора.

2) x + у = 35.

3) 0,6x + 0,8у (количество соли в получившемся растворе).

4) 0,6x + 0,8у = 35 ∙ 0,72.

0,6x + 0,8у = 25,2.

5)

Решив эту систему, получим, что х = 14 и у = 21.

Ответ: 14 мл 60 %-ного раствора и 21 мл 80 %-ного раствора.

Рассмотрим арифметический способ, который использовался в старину.

1) Найдем разность между процентным содержанием соли в каждом из имеющихся растворов и полученном растворе:

72 % – 60 % = 12 %;

80 % – 72 % = 8 %.

2) Эти результаты показывают, что 60 %-ного раствора нужно взять 8 частей, а 80 %-ного – 12 частей, то есть растворы должны быть взяты в отношении 2 : 3.

Поскольку в результате получим 35 мл раствора, то 60 %-ного взяли 14 мл, а 80 %-ного – 21 мл. [5]

Задача 8. Сразу после сбора урожая процентное содержание воды в бананах составляет 75%. После их перевозки процентное содержание воды в них становится равным 70%. Сколько килограммов бананов надо приобрести, чтобы после перевозки осталось 2500 кг бананов? [6]

Решение. Определим содержание так называемого «сухого вещества»: после сбора урожая его содержится 25%, после перевозки – 30%. Его масса после перевозки составит 2500 : 100 · 30 = 750 кг, но т. к. она остаётся неизменной и после сбора урожая это 25%, то нужно собрать 3000 кг бананов.

О т в е т: 3000 кг.

Задача 9. Смешав 25-процентныйи и 95-процентный растворы кислоты добавив 20 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси? [7]

Заключение

Задачи, которые мы решили,— это так называемая задача на концентрацию. Концентрацией раствора называют отношение массы содержащегося в нем сухого вещества к массе раствора, выражен­ное в процентах. С процентами приходится иметь дело и при реше­нии многих других задач, например задач на вычисление прибыли с банковских вкладов, дохода от инвестиций, на расчет объемов вы­полненных работ. Все такие задачи нетрудно решить, если вы уме­ете выражать проценты обыкновенной или десятичной дробью и ре­шать главную задачу на проценты — находить процент от заданной величины. Иногда удобно решать их или с помощью пропорции или системой уравнений. И тот и другой способы широко применяются при решении химических задач.

Литература

1. Дорофеев Г. В., Суворова С. Б. и др. Алгебра: учебник для 8 класса общеобразовательных учреждений. — М.: Просвещение, 2010. — 288 с.

2. Дюмина Т. Ю. Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. I полугодие.— Волгоград: Учитель, 2008. —205 с.

3. Дюмина Т. Ю. Математика. 6 класс: поурочные планы по учебнику Г. В. Дорофеева, С. Б. Суворовой, И. Ф. Шарыгина и др. Часть 1. — Волгоград: Учитель, 2006. — 235 с.

4. Калинина М. Ф. Алгебра. 7 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. — Волгоград: Учитель, 2008. — 223 с.

5. Дюмина Т. Ю. Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г. В. Дорофеева. II полугодие.— Волгоград: Учитель, 2009. —263 с.

6. Под редакцией Лысенко Ф.Ф. и Калабухова С.Ю. Математика 9 класс. Подготовка к ОГЭ-2016. 40 тренировочных вариантов. – Ростов-на-Дону: Легион, 2015. – 400 с.

7. Под ред. Ященко И.В. ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов. – М.: Издательство «Национальное образование», 2016. – 256 с.

Просмотров работы: 17501

МКУ
«Районное управление образования»

Администрации
МО «Кабанский район»

МАОУ
«Селенгинская гимназия»

Способы
решения задач на концентрацию веществ

в
растворах, смесях и сплавах

  Автор работы: Пахомова
Аурика Алексеевна

                                               
Ученица 9 класса Б

    Научный руководитель: Фаркова
Мария Николаевна

                                              
Учитель математики

2016
г

Оглавление

Введение	2
Основная часть	3
1.  Способы решения задач на концентрацию веществ в растворах, смесях и сплавах	3
2.  Решение одной задачи разными способами	5
3. Апробация	7
Заключение	8
Список литературы Приложение	10 11

Введение

В повседневной жизни мы
часто сталкиваемся с ситуациями, когда требуется смешать различные жидкости,
растворы, порошки, разбавлять что – либо водой. В математике уделяется большее
внимание таким процессам. Выделяют такой тип задач как задачи на смеси, связанные
со смешением, сплавлением веществ с различным содержанием в них некоторого
металла или соединением кислот разной концентрации и так далее.

Задачи данного типа все
чаще встречаются  в КИМах для подготовки и проведения экзамена по математике.
Решая один из тестов ОГЭ, я столкнулась с такой задачей, которая вызвала у меня
затруднение. Решив ее табличным способом, который мы использовали на уроках математики,
я не была уверена в полученном ответе, поэтому было необходимо выполнить
проверку, решив данную задачу другим способом. И здесь я поняла, что других
способов решения данной задачи я не знаю.

Тогда я решила
познакомиться с другими способами решения задач на концентрацию веществ, в
растворах, смесях и сплавах.  Более того, при решении задач данного типа четко
прослеживается взаимосвязь математики с другими различными школьными
дисциплинами, например, такими, как физика, химия и экономика. А значит, умение
решать задачи на концентрацию позволит легче ориентироваться и в других сферах.
Это и доказывает актуальность выбранной и рассматриваемой мной темы.

Объект исследования:
задачи на концентрацию веществ в растворах, смесях и сплавах.

Предмет исследования:
способы решения задач на концентрацию веществ в растворах, смесях и сплавах.

Цель исследования: рассмотреть способы решения задач на концентрацию веществ в
растворах, смесях и сплавах и научиться их применять.

Гипотеза: знание различных способов решения задач данного типа поможет
учащимся избавиться от трудностей при их решении, используя наиболее понятный и
удобный для них способ, что позволит более качественно подготовиться к сдаче
экзамена.

Для достижения
поставленной цели исследования и проверки достоверности сформулированной
гипотезы необходимо решить следующие задачи:

1. Рассмотреть различные способы
решения задач на концентрацию веществ в растворах, смесях и сплавах

2. Составить рекомендации
для решения задач в зависимости от используемого способа;

3. Рассмотреть применение
изученных способов при решении одной задачи;

Методы исследования:

1.Сравнительно-сопоставительный
анализ математической и учебной литературы;

2. Систематизация
способов решения;

3. Качественный и
количественный анализ результатов.

Основная
часть

1.  Способы решения задач на концентрацию
веществ в растворах, смесях и сплавах

1. «Метод чаш»

Рекомендации по применению данного
способа:

1) Изобразить каждый сплав (раствор,
смесь) в виде прямоугольника, разбитого на фрагменты;

2) Заполнить получившиеся прямоугольники в
соответствии с условием задачи:

·        
Над каждым «маленьким» прямоугольником
указать соответствующие компоненты сплава (смеси, раствора);

·        
Внутри прямоугольников вписать процентное
содержание соответствующего компонента. (Если сплав (смесь, раствор) состоит из
двух компонентов, то достаточно указать процентное содержание одного из них);

·        
Под прямоугольником записываем массу (или
объем) соответствующего сплава (или компонента);

3) Учитывая, что масса сплава (раствора,
смеси) нескольких веществ равна сумме масс компонентов, составить уравнение;

4) Решить уравнение.

Данный способ является
весьма удобным, так как зрительное восприятие данных, расположенных в
определенном задуманном порядке, позволяет компактно представить процессы
соединения растворов, упростить составление уравнения, а также облегчить процесс
ее решения. А так же я заметила, что составленное уравнение получается точно
таким же, что и при использовании табличного способа, из чего можно сделать
вывод, что эти способы очень похожи, отличие только в представлении данных из
условия задачи [1].

2. «Метод креста» или «Конверт Пирсона»

Рекомендации по применению данного
способа:

1) Записать одну над другой массовые доли
растворенного вещества в исходных растворах, слева между ними – его массовую
долю в растворе, который нужно приготовить;

2)  Вычесть по диагонали из большего
меньшее значение. (Разности их вычитаний показывают массовые доли для первого и
второго растворов, необходимые для приготовления нужного раствора);

3) Составить пропорцию и найти массу одной
части;

4) Найти массы исходных растворов.

Данный
способ является очень удобным при решении задач, в которых для приготовления
раствора, с определенной массовой долей растворенного в нем вещества требуется
смешением двух других растворов иной концентрации. Решить подобные задачи
возможно путем проведения достаточно сложного и трудоемкого арифметического
расчета. Однако это потребует большого количества времени и сил и в итоге будет
нерационально и малопродуктивно. Поэтому в таких ситуациях лучше применять
диагональную модель, называемую правилом «креста», что позволит прийти к
правильному ответу намного быстрее [2].

3. «С помощью применения формул»

Рекомендации по применению данного
способа:

1) Введем обозначения:

 –
процентное содержание вещества в исходной первой смеси (растворе или сплаве),

 –
процентное содержание вещества в исходной второй смеси (растворе или сплаве),

 –
процентное содержание вещества в получившейся или требуемой смеси (растворе или
сплаве),

 –
масса первой смеси,

 –
масса второй смеси,

 –
масса получившейся или требуемой смеси.

2) Составим равенство:

 или
.

3) Выразив из данного
равенства интересующую нас величину, получим ответ.

              [1].

4. «Метод площадей равновеликих
прямоугольников»

Рекомендации по применению данного
способа:

1. Построить диаграмму по заданному
условию: в горизонтальном направлении отложить массу сплава (раствора, смеси),
а в вертикальном — концентрацию сплава (раствора, смеси) или число долей
вещества в сплаве.

2. Построить равновеликие прямоугольники.

3. Составить уравнение, приравняв их
площади.

Данный способ удобно
применять при решении задач, где одна из рассматриваемых величин является
произведением двух других, которое можно наглядно представлять в виде площади
прямоугольника [2].

Вывод:
Таким образом, в данном разделе были рассмотрены различные способы решения
задач на концентрацию. Конечно, существуют и другие, но эти мне показались
более интересными, понятными и рациональными.

2. 
Решение одной задачи разными способами

Рассмотрим
задачу: Имеется два сплава. Первый из них
содержит 10% никеля, а второй – 30% никеля. Из двух данных сплавов получили
третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса
исходного второго сплава больше массы первого? [5]

Решим данную задачу
разными способами, придерживаясь рекомендаций, которые представлены выше

1. «Метод чаш»

Изобразим каждый из
сплавов в виде прямоугольника, разбитого на части согласно количеству входящих
в состав сплава элементов и заполним получившиеся прямоугольники в соответствии
с условием задачи.

Сплав состоит из никеля и
еще одного неизвестного компонента.

Введем обозначения:  х
кг – масса первого сплава;

                                     
(200 – х) кг – масса второго сплава.

Переведем проценты в
десятичную дробь: 10% = 0,1; 30% = 0,3; 25% = 0,25. Далее составим и решим уравнение:

,

,

,

.

Масса первого сплава
равна 50 кг, масса второго сплава равна 200 – 50 = 150 кг.

.

Ответ: масса второго
сплава на 100 кг превышает массу первого сплава.

2. «Метод креста» или «Конверт Пирсона»

Запишем
друг под другом содержание никеля в исходных сплавах, посередине слева от них –
процентное содержание никеля в новом сплаве, образовавшемся в результате
смешения двух, данных изначально.

Имеем
две пары чисел: 25 и 10, 25 и 30. Далее согласно схеме вычитаем из одного числа
пары другое и записываем полученные значения рядом, но поменяв строчки местами
(накрест).

Из 10-% сплава требуется
взять 5 частей, а из 30-% сплава – 15 частей. Составляем пропорцию: (кг) – масса одной части.

Соответственно первый
сплав – 5 частей – кг, второй сплав – 15 частей – кг. Второй сплав на 100 кг больше первого.

Ответ: масса второго
сплава на 100 кг превышает массу первого сплава.

3. «С помощью применения формул»

1) Введем обозначения:                

2) Подставляем данные
значения в формулу:

3) Решим полученное уравнение:

,    
,    ,

,

,

,

,

.

Ответ: масса второго
сплава на 100 кг превышает массу первого сплава.

4. «Метод площадей равновеликих
прямоугольников»

Построим диаграмму по заданному условию: в
горизонтальном направлении отложить массу сплава, а в вертикальном —
концентрацию сплава.

Зная, что равновеликие прямоугольники
имеют равные площади, составим уравнение.

Масса первого сплава
равна 50 кг,

Масса второго сплава
равна 200 – 50 = 150 кг.

.

Ответ: масса второго
сплава на 100 кг превышает массу первого сплава.

Вывод:
Таким образом, данную задачу можно решить, применяя несколько различных
способов, каждый из которых имеет свои определенные преимущества. При этом в
ходе решения удалось доказать, что правильность конечного ответа не зависит от
выбранного способа.

3. Апробация

Изучив способы  решения
задач на концентрацию, я решила поделиться полученными знаниями со своими
одноклассниками. Но перед этим я провела опрос, чтобы узнать вызывают ли задачи
данного типа у них затруднения и какие способы решения задач они знают.
Результаты получились следующие:

	да	нет
Вызывают ли у вас затруднения задачи на концентрацию?	60%	40%
Какие способы решения данных задач вы знаете?
Табличный	100%
Метод чаш	26%
Метод креста	0%
Метод площадей равновеликих прямоугольников	0%
С помощью формул	0%

После чего я провела для
своих одноклассников «мастер-класс» по решению задач данного типа разными
способами. После чего мне стало интересно остались ли у них затруднения при
решении задач, и какой же способ для них является более понятным и удобным. Для
этого я предложила им решить задачу любым понравившимся им способом. Результаты
получились следующие:

	да	нет
Вызывают ли у вас затруднения задачи на концентрацию?	6%	94%

Таким образом, можно
сделать вывод, что после проведенного мастер класса задачи на смеси не вызывают
особых затруднений у моих одноклассников, а так же большинство учащихся  отдали
свое предпочтение, «методу чаш», считая его более понятным, удобным и
рациональным.

Заключение

В ходе исследования:

Ø  мной
были рассмотрены несколько различных методов решения задач на концентрацию
веществ в растворах, смесях и сплавах;

Ø  составлены
рекомендации для решения задач в зависимости от используемого способа, которые я представила в виде таблицы;

Ø  рассмотрено
применение изученных способов при решении задач;

Ø  доказано,
что прийти к верному ответу задачи можно, используя любой из рассмотренных выше
способов решения.

Ø  проведен
«мастер класс» по решению задач  данного типа для одноклассников;

Ø  выявлен
способ наиболее удобный и понятный для учащихся.

    
В заключении хотелось бы отметить, что моя гипотеза нашла свое подтверждение,
так как знание нескольких различных способов позволит мне и моим одноклассникам
справиться с такими заданиями на экзамене намного быстрее и качественнее,
используя удобный для понятный для себе способ, а так же будет возможность
перепроверить себя, решая задачу другим путем.

    
В дальнейшем я планирую продолжить работу по данной теме и разработать сборник
задач на концентрацию веществ в растворах смесях и сплавах, который поможет мне
и выпускникам гимназии лучше подготовиться к сдаче экзамена.

Список
литературы

1. Городнова О. А. Учимся решать задачи на смеси и
сплавы, г-та «Математика» №36, 2004 г

2. Захарова, А.Е. Учимся решать задачи на
смеси и сплавы. Математика для школьников. 2006.-С.18-21

3. Ковалева Т.И., Бузулина О.Л., Безрукова
Ю.А. Математика: тренировочные тематические задания повышенной сложности с
ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного
экзаменов.– Волгоград: Учитель, 2009. – 494 с.

4. Мальцев Д.А., Мальцева Л.И., Каибханова
С.З. и др. Математика 9 класс. Предпрофильная подготовка: учебно- методическое
пособие. –Ростов н/Д: Издатель Мальцев Д.А, 2012. –

208 с.

5. Прокопенко Н. И.
Задачи на смеси и сплавы / Н.И. Прокопенко. — М.: Чистые пруды, 2010. – 215 с.

6. Райхмист Р.Б. Задачник по математике
для учащихся средней школы и поступающих в вузы (с решениями и ответами):
Учеб.пособие. – М.: Московский лицей, 2009. – 304 с.

7. Шевкин А.В. Текстовые задачи: 7 – 11
классы: Учебное пособие по математике. – М.: «ТИД «Русское слово – РС», 2003. –
184 с.