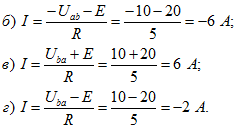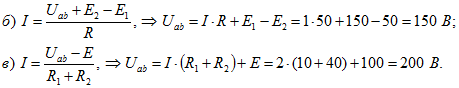Для нахождения напряжения в конечных точках проволоки, необходимо воспользоваться законом Ома: U = I × R, где U — напряжение, I — сила тока, а R — сопротивление проводника.
Нам дана плотность тока в проволоке — 3 мкА/мм² и её длина — 9 м. Сначала переведём плотность тока в амперы на метр, умножив на 1000 (1 мм² = 10⁻⁶ м²):
3 мкА/мм² × 1000 = 3 мА/м².
Сопротивление проводника можно вычислить по формуле:
R = ρ × L/S,
где ρ — удельное сопротивление материала проводника, L — длина проводника, а S — его площадь сечения.
Удельное сопротивление материала равно 2,8×10⁻⁸ Ом·м, следовательно,
R = 2,8 × 10⁻⁸ Ом·м × 9 м / S
Нам не дана площадь сечения провода, поэтому она может быть любой. Поэтому нам нужно использовать дополнительную информацию о напряжении в проводе, чтобы определить площадь сечения провода.
Согласно уравнению мощности, мощность, расходуемая на проводнике, равна произведению напряжения на силу тока:
P = U × I.
Мы знаем, что сила тока равна 3 мА на каждый квадратный метр площади провода. Тогда по формуле мощности,
P = U × 3 × 10⁻³ Вт/м².
Поскольку мощность не указана в задаче, предположим, что она составляет 1 Вт.
1 Вт = U × 3 × 10⁻³ Вт/м² × S.
Сокращая и выражая S, получим:
S = 1 Вт / (U × 3 × 10⁻³ Вт/м²).
Теперь мы можем выразить сопротивление R через площадь сечения провода:
R = 2,8 × 10⁻⁸ Ом·м × 9 м / S = 2,8 × 10⁻⁸ Ом·м × 9 м / (1 Вт / (U × 3 × 10⁻³ Вт/м²)) = 84 ×10⁻⁹ м² × U / Вт.
Теперь мы можем объединить уравнения для напряжения и сопротивления:
U = I × R = 3 мА/м² × 84 ×10⁻⁹ м² × U / Вт = 252 ×10⁻¹² В/м² × U.
Разделим обе части на 252 ×10⁻¹² В/м²:
U = U × 3 мА/м² ÷ 252 ×10⁻¹² В/м².
Упрощая это уравнение, находим:
U = 35,7 В.
Значит, при плотности тока в проволоке 3 мкА/мм² и ее длине 9 м, необходимое напряжение в конечных точках проволоки равно 35,7 В. Ответ округляем до сотых — получается 35,70 В.
Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Сопротивление
Формула механической мощности — средняя и мгновенная мощность
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Для переменного тока
Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.
Переменный ток
Im=Vm/Z
В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).
Vm = ImZ и Vm = ImR
Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.
Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.
Интегральная форма
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Закон Ома для неоднородного участка цепи
Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:
$ E_{эдс} = {A_{cт}over q} $ (1).
Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.
Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:
$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).
Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
$ U_п = φ_1 – φ_2 $ (3).
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
$ I = {U over R} $ (4).
Рис. 2. Портрет Георга Ома.
Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:
$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).
Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.
В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Единицы измерения в формуле
Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы
В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Физика > ЭДС и конечное напряжение
Рассмотрите связь электродвижущей силы и конечного напряжения в электрической цепи: роль внутреннего сопротивления, разность потенциалов, формула и схемы.
Конечное напряжение (напряжение на выходе источника) основывается на электродвижущей силе и внутреннем сопротивлении.
Задача обучения
- Переведите соотношение между ЭДС и конечным напряжением в формулу.
Основные пункты
- Электродвижущая сила отображает разность потенциалов источника в момент, когда ток лишен движения.
- Конечное напряжение – выход напряжения в устройстве, измеренное через клеммы.
- Формула расчета: V = ЭДС — Ir.
Термины
- Конечное напряжение – выход напряжения в устройстве, измеряемое на клеммах.
- Электродвижущая сила (ЭДС) – напряжение, сформированное батареей или магнитной силой в соответствии с законом Фарадея.
- Разность потенциалов – отличие в показателях потенциальной энергии между двумя точками в электрическом поле.
Если вы забудете выключить фары на машине, то со временем они потускнеют. Причина – разряд батареи. Почему же они просто не мигают при потере энергии? Постепенное затухание говорит о том, что конечное напряжение снижается по мере расхода заряда. Все дело в том, что у всех источников напряжения есть две главные части: источник электрической энергии и внутреннее сопротивление.
Электродвижущая сила
Все источники напряжения формируют разность потенциалов и могут отправлять ток при подключении к сопротивлению. Если брать небольшой масштаб, то из-за этого отличия создается электрическое поле, влияющее на заряды и вызывающее ток. Мы называем это отличие электродвижущей силой (ЭДС). Но не думайте, что перед нами «сила» в привычном понятии. Это особая разновидность разности потенциалов источника, когда ток лишен движения. Измеряется в вольтах.
ЭДС связана с источником разности потенциалов, но отличается от конечного напряжения при проходе тока. К примеру, напряжение на аккумуляторе будет меньшим, чем ЭДС. Если конечное напряжение можно вычислить без подачи тока, то оно приравнивается к ЭДС.
Конечное напряжение
Выход напряжения из устройства измеряется на клеммах и именуется конечным напряжением (V). Его вычисляют по формуле:
Любой источник напряжения обладает ЭДС, связанной с источником разности потенциалов. Также оно настраивается на сопротивление (r), связанное с конструкцией. Здесь видны выходные клеммы, по которым измеряют конечное напряжение (V). Так как V = ЭДС — Ir, конечное напряжение приравнивается к ЭДС, если ток отсутствует
V = ЭДС – Ir (r – внутреннее сопротивление, I – протекающий во время измерения ток).
I положителен, если ток течет от положительной клеммы. Чем больше ток, тем меньше конечное напряжение. Также конечное напряжение уменьшается при росте внутреннего сопротивления.
Применение закона Ома к расчету линейных электрических цепей постоянного тока
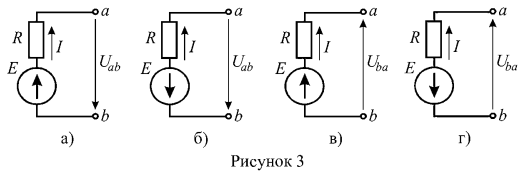
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
Аналогично определяются токи в схемах б, в, г рисунка 3:
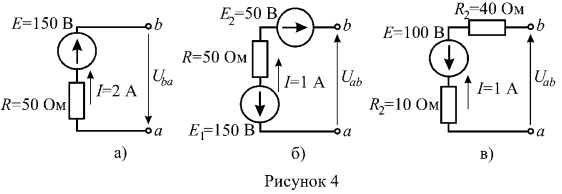
2. Найти напряжение между зажимами нетвей (рисунок 4).
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
откуда выразим напряжение на зажимах:
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
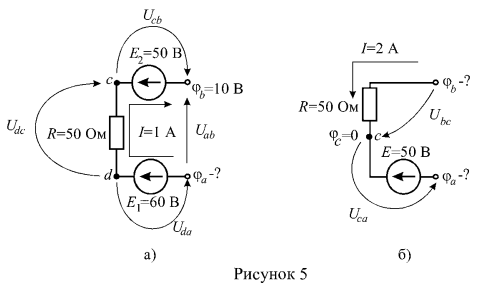
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
откуда выразим напряжение на зажимах ветви:
Если представить напряжение как разность потенциалов:
тогда при известных параметрах цепи, токе и потенциале определим потенциал
:
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и тогда, зная потенциал , определим потенциал точки С:
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
тогда
Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС
. Напряжение
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
откуда следует, что
или
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
откуда следует
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
. Определить величину сопротивления резистора
.
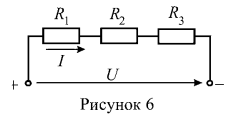
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
или, согласно закону Ома:
По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:
По закону Ома напряжение на зажимах определится:
тогда величина сопротивления резистивного элемента:
5. Определить показания вольтметров цепи (рисунок 7), если .
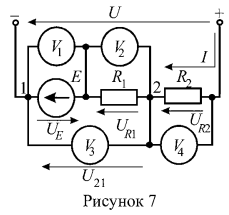
Ток в цепи определим по закону Ома:
Вольтметр показывает напряжение на источнике ЭДС Е:
Вольтметры показывают величину падения напряжения на резистивных элементах
:
Вольтметр , показывает напряжение на участке 2 — 1
, которое определим как алгебраическую сумма напряжений
:
6. Ток симметричной цепи (рисунок 
, внутреннее сопротивлении источника ЭДС
. Определить ЭДС Е и мощность источника энергии.
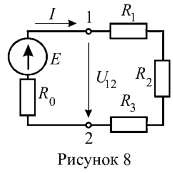
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
Мощность, развиваемая источником энергии, определится:
Конечное напряжение
Cтраница 1
Конечное напряжение в шпильке определяют из выражения ш Р / 1Ш; если полученное значение превышает допускаемое, увеличивают диаметр шпильки.
[1]
Конечное напряжение это есть то напряжение на зажимах батареи в замкнутой цепи, при котором следует прекратить разряд.
[2]
Конечное напряжение — 1 В на аккумулятор.
[4]
Конечное напряжение определяется на основе особенностей электрохимической системы и условий эксплуатации источника тока. Обычно под конечным напряжением подразумевается такое напряжение, ниже которого эксплуатация источника тока не целесообразна.
[5]
Конечное напряжение по-режнему составляет 2 05 или 1 60 В. Превышение этих прсдс-оп приводит через короткое время к энергичному образопанию ислорода на оксидносеребряном электроде и, как следствие, к реждевременному разрушению сепараторной пленки. При за-яде СК-аккумулятора напряжение 1 60 В иногда достигается скоре после начала заряда.
[6]
Конечное напряжение для 286 — 7 — 316 составляет 1 В, для 332 — f — 465 — 0 85 В.
[8]
Конечное напряжение определяется на основе особенностей электрохимической системы и условий эксплуатации источника тока. Обычно под конечным подразумевается такое напряжение, ниже которого эксплуатация источника тока нецелесообразна и разряд следует прекратить. Конечное напряжение первичных элементов находится в пределах 0 5 — 3 0 В.
[9]
Конечное напряжение батареи из последовательно соединенных аккумуляторов равно произведению напряжения отдельного аккумулятора на число аккумуляторов.
[10]
Предельные конечные напряжения, до которых разрешается безболезненно разряжать данный тип аккумулятора, обычно указываются в заводских инструкциях. В табл. 32 приведены конечные напряжения для некоторых типов аккумуляторов.
[11]
Конечное напряжение U измеряется в современных приборах с помощью электрометрического усилителя. Его входной ток, а также токи утечки конденсатора и соединительных проводов должны быть настолько малыми, чтобы вызванное ими снижение напряжения не влияло на точность отсчета. Наибольшие трудности вызывает создание выключателей. Их сопротивление в разомкнутом состоянии должно быть по порядку величины не меньше остальных сопротивлений изоляции, а сопротивление выключателя 2 при пропускании тока должно быть по возможности малым или по крайней мере постоянным. Вместе с тем разброс времени размыкания должен быть меньше требуемого разрешения по времени. Возможны как электронные переключатели [33, 35], так и механические контакты.
[12]
Конечное напряжение железо-никелевых аккумуляторов часто принимается равным 1 00 0 на элемент независимо от режима разряда.
[13]
Конечное напряжение полностью заряженной аккумуляторной батареи, определяющее ток перезарядки аккумулятора при данном напряжении, поддерживаемом регулятором, в большой степени зависит от температуры электролита. При обычной подкапотной установке температура электролита изменяется в очень широких пределах — от отрицательных температур до 60 С и более. Для наружной установки аккумуляторной батареи характерны систематическая недозарядка батареи в зимнее время и уменьшение надежности запуска двигателя. Происходит эт вследствие постепенного снижения температуры электролита до температуры окружающего воздуха и повышения конечного зарядного напряжения. Так, например, при температуре воздуха от — 10 до — 20 С аккумулятор может зарядиться только до 60 — 70 % емкости, если напряжение генератора будет 15 в. Следовательно, величина регулируемого напряжения, определяющая режим зарядки аккумуляторной батареи, должна быть различна в зависимости от температурных условий эксплуатации.
[14]
Страницы:
1
2
3
4
5