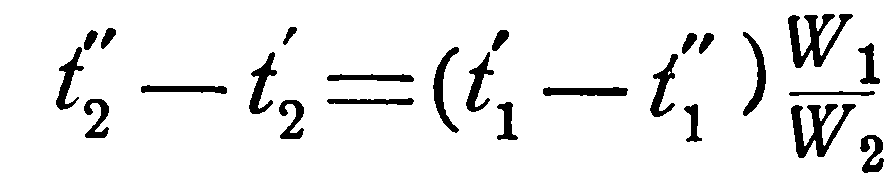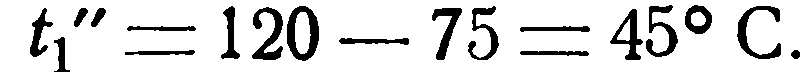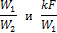Как найти конечную температуру воздуха

Все неприличные комментарии будут удаляться.

все для проектирования

Формула расчета конечной температуры воды после смещения холодной и горячей:

где: Тс — температура смещенной воды, град.

М1 — масса холодной воды, кг

М2 — масса горячей воды, кг

Т1 — температура холодной воды, град.

Т2 — температура горячей воды, град.

Пример 1:

холодная вода 10 литров температурой 5 град смешивается с горячей водой 8 литров 60 градусов.

Необходимо определить конечную температуру воды. Подставляем все значения в формулу 1:

Формула расчета количество холодной и горячей воды в зависимости от температуры:

Бывает задача стоит в обратном направлении. Когда наоборот известно какую температуру необходимо иметь на выходе и общий вес воды, но не известна масса холодной и горячей воды. Тогда из формула 1 выводим новую формулу:

Пример 2:

из циркуляционного душа воды выходит температурой 36 градусов и объемом 40 литров. Необходимо определить количество холодной и горячей воды.

Как правило холодная вода имеет расчетную температуру 5 градусов. Горячая вода — 60 градусов.

Подставляем значения в формулу 2 и 3:

М1=(36*40-60*40)/(5-60)=17,45 литров холодной воды

М2=40-17,45=22,55 литров горячей воды

Удачного Вам дня! И успешных проектов!

Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это — так называемый поверочный расчет.

При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W₁ и W₂ и начальные температуры t₁’ и t₂’, а искомыми: конечные температуры t₁” и t₂” и количество переданного тепла Q.

В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:

(2.13)

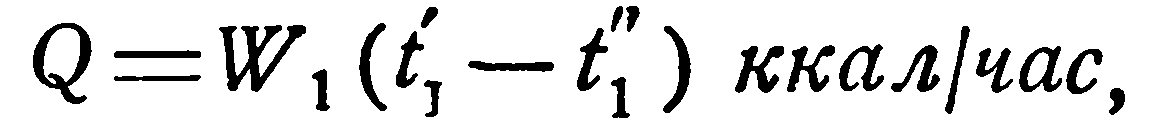
откуда конечная температура ее t₁” определяется соотношением:

(a)

Соответственно для холодной жидкости имеем:

(2.14)

(b)

Если принять, что температуры рабочих жидкостей меняются по линейному закону, то

(с)

Вместо неизвестных t₁” и t₂” подставим их значения из уравнений (а) и (b), тогда получим:

(d)

Произведя дальнейшее преобразование, имеем:

(e)

откуда окончательно получаем:

(2.15)

Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t₁” и t₂”.

Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.

1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:

(2.16)

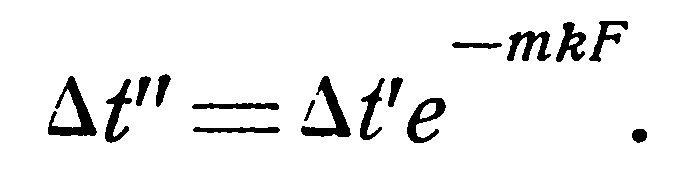
Имея в виду, что

и, что в конце поверхности нагрева Δt” = t₁’ – t₂’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:

(2.17)

Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:

(2.18)

(2.19)

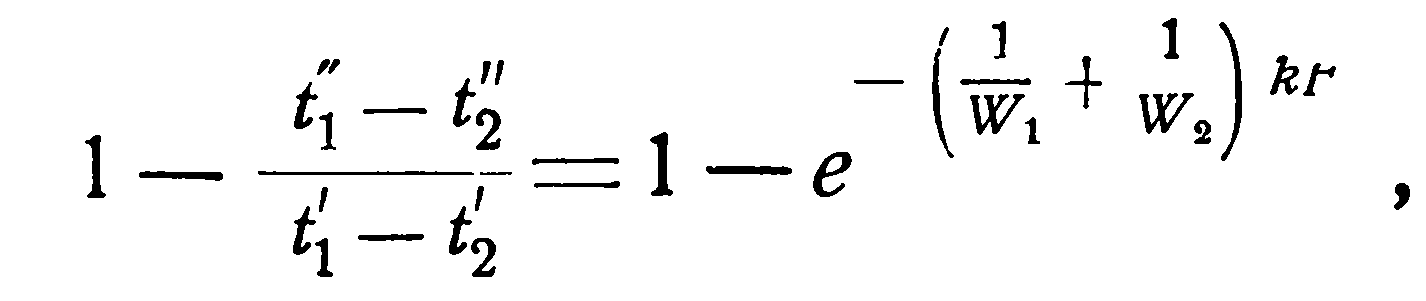
[см. разд.2.1 уравнение (2.5)].

то, подставляя это значение в левую часть уравнения (2.19), получаем:

(2.20)

Последнее уравнение, показывает, что изменение температуры горячей жидкости δt₁ равно некоторой доле П располагаемого начального температурного напора, t₁’ – t₂’; эта доля зависит только от двух безразмерных параметров 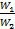и .

Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:

(2.21)

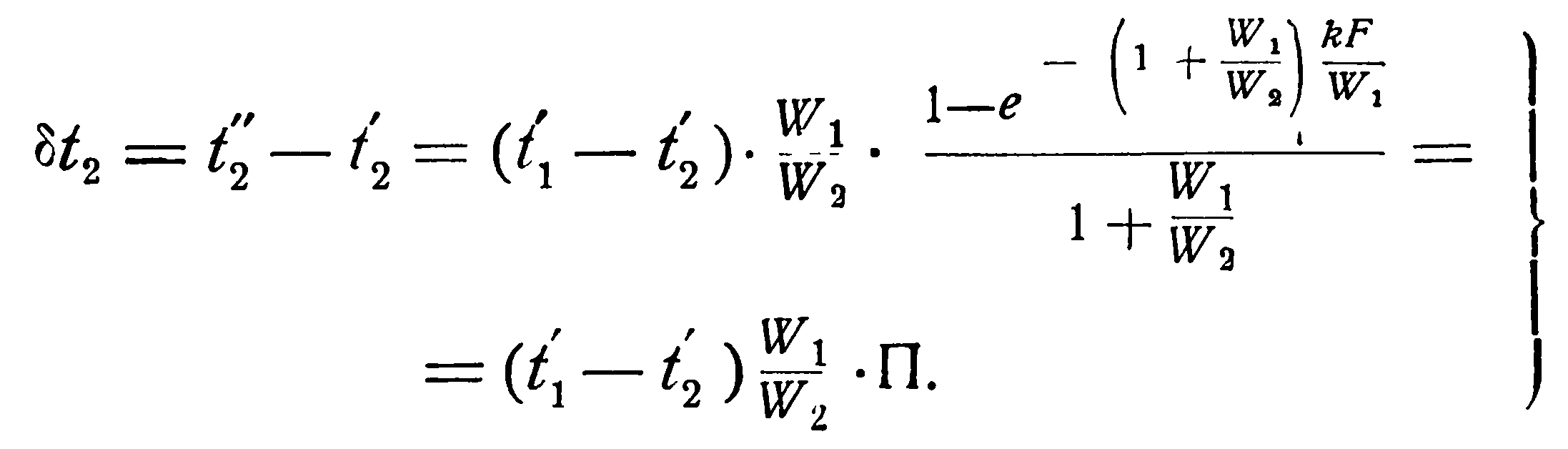
Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:

(2.22)

Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:

(2.23)

Значение функции приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение F_x.

Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м 2 . Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V₁= 0,25 м 3 /час, γ₁ = 1100 кг/м 3 , c_p1 = 0,727 ккал/кг °С и t₁’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t₂’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м 2 час °С.

Соответствующее значение функции П находим из рис.2.5:

Рис. 2.5. — вспомогательная функция для расчета конечной температуры при прямотоке

Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:

Следовательно, конечная температура ее равна:

Количество переданного тепла в час определится по уравнению (2.23)

Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W₂ (t₂” — t₂’), откуда

2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:

(2.24)

(2.25)

(2.26)

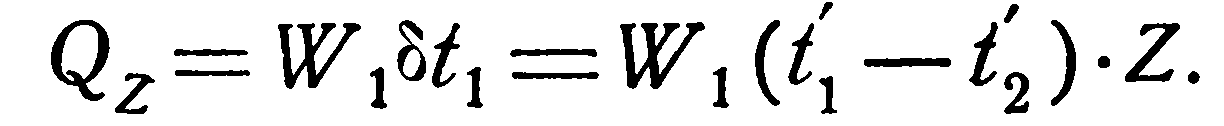
В частном случае, когда формулы

(2.24) – (2.26) принимают вид:

(2.27)

(2.28)

(2.29)

Значение функции 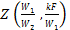приведено на рис. 2.6.

Рис. 2.6. — вспомогательная функция для расчета конечной температуры при противотоке

Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на F_x, а в знаменателе остается значение полной поверхности F.

Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м 2 час °С), то получим следующие соотношения:

Из рис. 2.6 находим значение функции Z:

Изменение температуры горячей жидкости равно [уравнение (2.24)]:

Конечная температура ее:

Изменение температуры холодной жидкости [уравнение (2.25)];

Конечная температура ее:

Количество переданного тепла в час [уравнение (2.26)]:

Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.

3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов

характер изменения которой графически показан на рис. 2.7.

Рис. 2.7. -сравнение прямотока с противотоком

Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при и при ) или если значение параметра — мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку , то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.

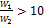
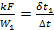
При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.

При конденсации паров;

(2.30)

(2.31)

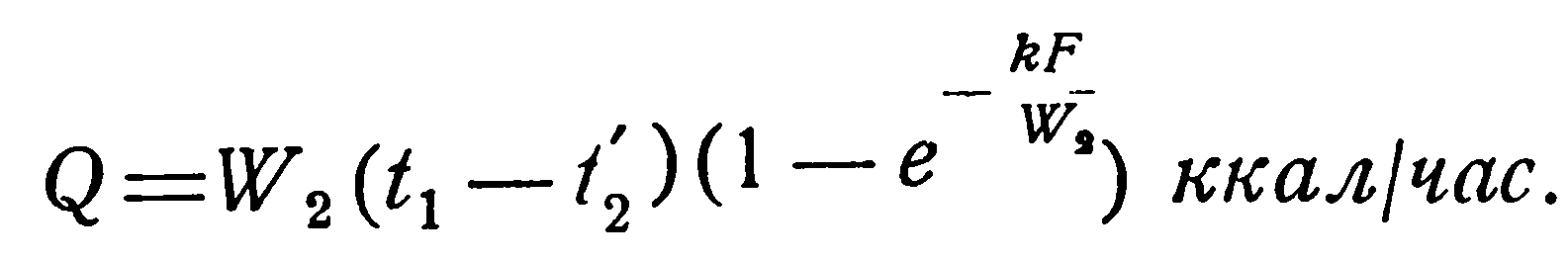
При кипении жидкостей:

(2.32)

(2.33)

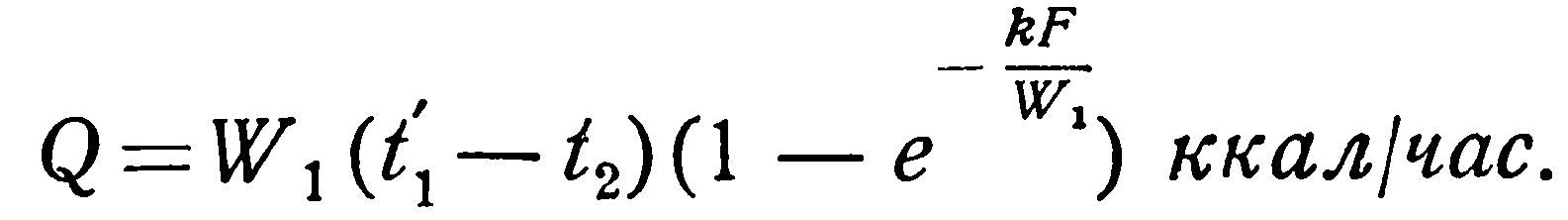
Вместо t₁ и t₂ в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции находятся из таблиц показательных функций.

В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.

4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.

Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.

Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.

Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:

(2.34)

Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.

При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Thermodynamics is the field of physics concerned with temperature, heat and, ultimately, energy transfers. Although the laws of thermodynamics can be a little tricky to follow, the first law of thermodynamics is a simple relationship between the work done, heat added, and the change in internal energy of a substance. If you have to calculate a change in temperature, it’s either a simple process of subtracting the old temperature from the new one, or it may involve the first law, the amount of energy added as heat, and the specific heat capacity of the substance in question.

What’s the Difference Between Heat and Temperature?

The key bit of background you need for a temperature calculation is the difference between heat and temperature. The temperature of a substance is something you are familiar with from everyday life. It’s the quantity you measure with a thermometer. You also know that the boiling points and melting points of substances depend on their temperature. In reality, temperature is a measure of the internal energy a substance has, but that information isn’t important for working out the change in temperature.

Heat is a bit different. This is a term for the transfer of energy through thermal radiation. The first law of thermodynamics says that the change in energy equals the sum of the heat added and the work done. In other words, you can give more energy to something by warming it up (transferring heat to it) or by physically moving or stirring it (doing work on it).

Simple Change in Temperature Calculations

The simplest temperature calculation you may have to do involves working out the difference between a starting and finishing temperature. This is easy. You subtract the final temperature from the starting temperature to find the difference. So if something starts at 50 degrees Celsius and finishes at 75 degrees C, then the change in temperature is 75 degrees C – 50 degrees C = 25 degrees C. For decreases in temperature, the result is negative.

The biggest challenge for this type of calculation occurs when you need to do a temperature conversion. Both temperatures must be either Fahrenheit or Celsius. If you have one of each, convert one of them. To switch from Fahrenheit to Celsius, subtract 32 from the amount in Fahrenheit, multiply the result by 5, and then divide it by 9. To convert from Celsius to Fahrenheit, first multiply the amount by 9, then divide it by 5, and finally add 32 to the result. Alternatively, just use an online calculator.

Calculating Temperature Change From Heat Transfer

If you’re doing a more complicated problem involving heat transfer, calculating the change in temperature is more difficult. The formula you need is:

Change in temperature = Q / cm

Where Q is the heat added, c is the specific heat capacity of the substance, and m is the mass of the substance you’re heating up. The heat is given in joules (J), the specific heat capacity is an amount in joules per kilogram (or gram) °C, and the mass is in kilograms (kg) or grams (g). Water has a specific heat capacity of just under 4.2 J/g °C, so if you’re raising the temperature of 100 g of water using 4,200 J of heat, you get:

Change in temperature = 4200 J ÷ (4.2 J/g °C × 100 g) = 10 °C

The water increases in temperature by 10 degrees C. The only thing you need to remember is that you have to use consistent units for mass. If you have a specific heat capacity in J/g °C, then you need the mass of the substance in grams. If you have it in J/kg °C, then you need the mass of the substance in kilograms.

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

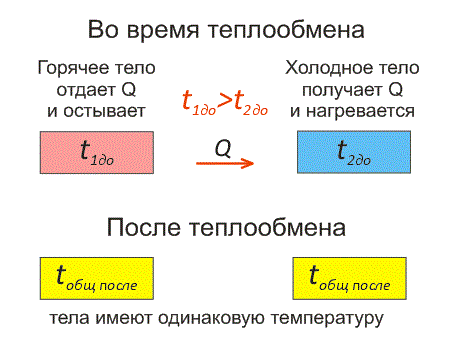
Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту).  Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]

(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.

(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_{1} + Q_{2} = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

• равными по модулю и
• имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]

При этом:

• Q для каждого нагреваемого тела будет обладать знаком «+»,
• Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

 Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]

2). Теперь запишем формулу для каждого количества теплоты:

[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]

[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]

Примечания:

1. (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
2. Массу воды переводим в килограммы;
3. Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
4. Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]

Проведем упрощение:

[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

[large t_{text{общ}} = 58,33 ]

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

• (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
• (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
• (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Выводы

1. Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
2. Когда тела будут иметь равную температуру, теплообмен прекратится;
3. Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
4. А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
5. Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
6. Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
7. В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
8. В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.