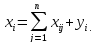Балансовые модели предназначены для анализа и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом. Если вспомнить историю народного хозяйства как Советского Союза и России, так и других развитых стран, то можно наблюдать, что в экономики многих государств, в разное время случались экономические кризисы разных крайностей от кризисов перепроизводства (США, середина ХХ века), до дефицита (Россия, конец ХХ века). Все эти экономические кризисы связаны с нарушением баланса между производством и потреблением. Из этих фактов видно, что баланс между произведенной продукцией и потреблением является важными критериями как для макроэкономики, так и для микроэкономики.
Экономико-математические модели баланса пытались выстроить многие экономисты и математики с самого начала возникновения проблемы, однако, наиболее полную балансовую модель удалось построить в 1936 г. американским экономи стом В. Леонтьевым (который после революции эмигрировал в США и за свою модель получил Нобелевскую премию в области экономики). Эта модель позволяла рассчитать баланс между несколькими взаимодействующими отраслями, хотя ее можно легко обобщить и для организаций микроэкономики, например, для вычисления баланса между несколькими взаимодействующими предприятиями или между подразделениями одного предприятия (например, цехами одного завода).
Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производ ства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции; а с другой — как потребитель продукции и своей, и произведенной другими отраслями.
Предположим, что рассматривается п отраслей промышленно сти, каждая из которых производит свою продукцию. Пусть общий объем произведенной продукции i -й отрасли равен 


Рассмотрим процесс производства за некоторый период времени (например, год). Так, как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то уравнение баланса между производством и потреблением будет иметь вид:

Уравнения (1) называются соотношениями баланса.
Можно также рассчитать такой показатель, как чистую продукцию 

Все, ранее рассмотренные показатели, можно записать в основную балансовую таблицу:

В результате, основная балансовая таблица, содержит четыре матрицы: матрица межотраслевых производственных связей 



Одной из задач балансового анализа является определение валового продукта 


Они получаются в результате деления всех элементов каждого столбца матрицы 


Если обозначить матрицу коэффициентов прямых затрат как 

Из последнего выражения можно найти значение конечного продукта при известном значении валового:

где 
Пример 1. Баланс четырех отраслей за предыдущий период имеет матрицу межотраслевых производственных связей вида 

Конечный продукт Y получается в результате вычитания из каждого элемента матрицы валовой продукции суммы элементов соответствующих строк матрицы 




Поставим теперь другую задачу: рассчитаем конечный продукт каждой отрасли на будущий период, если валовый продукт окажется равным 

По формуле (6) получим

Важнейшей задачей межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А (или при возможности рассчитать этот показатель) обеспечивает заданный вектор конечного продукта Y.
Из уравнения (6) можно выразить валовый продукт:

Матрица 

Пример 2. В некотором регионе имеются две основные отрасли народного хозяйства: машиностроение (м/с) и сельское хозяйство (с/х). Баланс этих отраслей за отчетный период определяется матрицами 


Предположим, что на будущий период планируется конечная продукция в объемах 



Найдем матрицу 
Определитель равен 

Транспонируем ее: 

Валовый продукт

Таким образом, нужно планировать валовый выпуск машиностроения в размере 221 ед., а сельского хозяйства в размере 254 ед.
Постановка
задачи. Пусть
имеется n
отраслей промышленности, каждая из
которых производит продукцию, которая
идет как для внутреннего потребления
данной отраслью и другими отраслями,
так и для конечного личного или
общественного потребления. Обозначим
хi
– общий
(валовый) объем продукции i-отрасли,
хij
– объем
продукции i-отрасли,
потребляемой j-отраслью,
yi
– объем
конечного продукта i-отрасли.
Имеем соотношение
баланса:
Введем
коэффициенты прямых затрат

Если считать, что эти коэффициенты
постоянны в течение некоторого периода
времени, тоxij
= aij
xj
, и соотношение баланса примет вид:

в матричном виде Х = А٠Х
+ У.
Задача
состоит в
нахождении такого вектора Х, который
при известной матрице прямых затрат А
обеспечивает конечный
продукт
У.
Решая
полученное матричное уравнение, находим
Х = (Е–А)–1
У.
Матрица
(Е – А)–1
называется матрицей
полных затрат.
Чтобы
матричное уравнение было разрешимо,
необходимо, чтобы матрица А была
продуктивной.
Есть несколько критериев продуктивности
матрицы. Например, если
максимум сумм элементов столбцов не
более 1 и хоть одна сумма строго меньше
1, то матрица продуктивна.
Пример
1.9. Решение
задачи поиска межотраслевого баланса
[3,
c.
99 – 104].
Имеется
две отрасли производства, в
таблице 1.9
указаны объёмы производства и потребления.
Таблица
1.9
|
Производство |
Потребление |
Конечный продукт |
Валовый |
|
|
Энергетика |
Машиностроение |
|||
|
Энергетика |
100 |
160 |
240 |
500 |
|
Машиностроение |
275 |
40 |
85 |
400 |
Необходимо
вычислить объем валового выпуска
продукции каждой отрасли, если конечный
продукт 1-й отрасли должен увеличиться
в 2 раза, 2-й
на
20 %.
Из
таблицы 1.9
имеем:
х1
= 500, х2
= 400, у1
= 240, у2
= 85, х11
= 100, х21
= 275, х12
=160, х22
= 40.
Построим
матрицу прямых затрат:
а11
=
=
= 0,2; а12 =
=
= 0,4;
а21
=
=
= 0,55; а22
=
=
= 0,1.
А
=
,
Е–
А =
–


Проверим
матрицу А на продуктивность:
0,2
+ 0,55 = 0,75 < 1, 0,4 + 0,1 = 0,5 < 1, т. е. матрица
А продуктивна.
Найдем
обратную к ней. Вычислим определитель:
0,8٠0,9
– 0,55٠
0,4
= 0,5.
Тогда,
Вычислим
по данным условия задачи новый вектор
конечного продукта
У = (У1,
У2):
У1
= 240٠2
= 480, У2
= 85 ٠(1+
0,2) = 102. Имеем Унов
=
Тогда
Х =
=

1.15.
В таблице
1.10 приведены
данные об исполнении баланса за отчетный
период в усл. ден. ед.
Таблица
1.10
|
Отрасль |
Потребление |
Конечный |
Валовый |
||
|
Сфера |
Лёгкая |
||||
|
Произ-водство |
Сфера |
7 |
21 |
72 |
100 |
|
Лёгкая |
12 |
15 |
63 |
100 |
Вычислить
необходимый объем валового выпуска
каждой отрасли, если конечное потребление
сферы обслуживания увеличится вдвое,
а лёгкой промышленности сохранится на
прежнем уровне.
1.16.
Продуктивна ли матрица А:
1)


1.17.
Экономика разделена на три отрасли. В
таблице 1.11
заданы коэффициенты прямых затрат и
конечная продукция отраслей.
Таблица
1.11
|
Отрасль |
Потребление |
Конечный |
|||
|
Сфера |
Лёгкая |
Сельское |
|||
|
Произ-водство |
Сфера |
0,3 |
0,25 |
0,2 |
56 |
|
Лёгкая |
0,15 |
0,12 |
0,03 |
20 |
|
|
Сельское |
0,1 |
0,05 |
0,08 |
12 |
Найти
объем валовой продукции каждой отрасли,
межотраслевые поставки, чистую продукцию
отраслей.
1.18.
Дана матрица полных затрат
Найти
приращение валового выпуска ∆Х,
обеспечивающее приращение конечной
продукции ∆У = (10, 30, 20).
1.19.
Отрасль состоит из 4-х предприятий;
вектор выпуска продукции и матрица
внутреннего потребления имеют вид:
Х
=

Пользуясь
моделью Леонтьева, найти вектор объемов
конечного продукта, предназначенного
для реализации вне отрасли.
1.20.
Данные баланса трех отраслей промышленности
за некоторый промежуток времени даны
в таблице
1.12.
Требуется найти объем валового выпуска
каждого вида продукции, если конечное
потребление увеличить соответственно:
1)
до 60, 70 и 30 единиц;
2)
на 30, 10 и 50 %.
Решить
задачу методом обратной матрицы.
Таблица
1.12
|
№ п/п |
Отрасль |
Потребление отрасли |
Конечный |
Валовый |
||
|
1 |
2 |
3 |
||||
|
1 |
Добыча |
5 |
35 |
20 |
40 |
100 |
|
2 |
Энергетика |
10 |
10 |
20 |
60 |
100 |
|
3 |
Машиностроение |
20 |
10 |
10 |
10 |
50 |
Соседние файлы в папке ПОСОБИЯ
- #
- #
20.03.201612.93 Mб33Уч. пособие по математике (Кремер).pdf
���� ����������� ������� — �������� �� ������,
����������� � �������������� � ��������� � �������������� �������
���������������� ���������: ����� ������ ���� ����� ������������ ������
�� n ��������, ����� ������������� ��� ����������� �
��������� ���� �������? ��� ���� ������ ������� ���������, � ����� �������,
��� ������������� ��������� ���������, � � ������ — ��� �����������
��������� � �����, � ������������� ������� ���������.
����� ����� ���������, ��� �������, ���������� � ��������
�������������� �������, � �������������� ������, ����������� ��
�������������, ����������� � 1936 �. ������������ �����������
�. ����������.
�����������, ��� ��������������� n
�������� ��������������, ������ �� ������� ���������� ���� ���������.
����� ��������� ���� �� ������ ���������������� ����������� ������ ��������
� ������� ���������, � ������ ����� ������������� ��� ����� ��������� (���
����� ������������� ������������) ������� � ������������� �����������.
���������� ������� ������������ �� ��������� ������
������� (��������, ���).
������ ��������� �����������:
- xi — ����� (�������) ����� ���������
i-� ������� (i = 1,2,…,n); - xij — ����� ��������� i-�
�������, ������������ j-� �������� � ��������
������������ (i,j = 1,2,…,n); - yi — ����� ��������� �������� i-�
������� ��� ������������������� �����������.
��� ��� ������� ����� ��������� ����� i-� �������
����� ���������� ������ ���������, ������������ n ��������� �
��������� ��������, ��
xi = (xi1 + xi2+ … +
xin) + yi , (i = 1,2,…,n).
��� ��������� (�� n ����) ����������
������������� �������. ����� ������������� �����������
������������� ������, ����� ��� ��������, �������� � ��� ���������,
����� ����������� ���������.
������ ������������ ������ ������:
aij = xij / xj ,
(i,j = 1,2,…,n),
������������ ������� ��������� i-� ������� ��
������������ ������� ��������� j-� �������.
����� ��������, ��� � ��������� ���������� �������
������������ aij ����� ����������� �
���������� �� ����������� ���������� ������������. ��� ��������
�������� ����������� ������������ ������ �� �������� �������,
�.�.
xij = aijxj , (i,j
= 1,2,…,n),
���������� ���� ����������� �� ���� ��������� ������
�������������� ������� �������� �������� ��������.
������ ����������� ������� ������ ���:
xi = (ai1x1 +
ai2x2 + … + ainxn) +
yi , (i = 1,2,…,n),
���������
| || | x1 | || | || | a11 | a12 | … | a1n | || | || | y1 | || | |||||||||
| || | x2 | || | || | a21 | a22 | … | a2n | || | || | y2 | || | |||||||||
| X | = | || | … | || | , | A | = | || | … | … | … | … | || | , | Y | = | || | … | || | , |
| || | xn | || | || | a1n | a2n | … | ann | || | || | yn | || |
���
- X — ������ �������� �������;
- A — ������� ������ ������ (��������������� ��� �����������
�������); - Y — ������ ��������� ��������.
����� ����������� ������� ����� �������� � ����:
X = AX + Y.
�������� ������ �������������� ������� �������
� ��������� ������ ������� �������� ������� X, �������
��� ��������� ������� ������ ������ A ������������
�������� ������ ��������� �������� Y.
��������� ��������� ��������� � ����:
(E — A) X = Y.
���� ������� (E — A) �������������,
�.�. �� ������������ �� ����� ����, �����:
X = (E — A)-1 Y.
������� S = (E — A)-1
���������� �������� ������ ������.
����� �������� ������������� ����� ���������
������� S = (sij), ����� ����������
���������� ��������� ��������� ��������:
| || | 1 | || | || | 0 | || | || | 0 | || | |||||||||||
| || | 0 | || | || | 1 | || | || | 0 | || | |||||||||||
| Y1 | = | || | … | || | , | Y2 | = | || | … | || | , | … | , | Yn | = | || | … | || | . |
| || | 0 | || | || | 0 | || | || | 1 | || |
����� ��������������� ������� �������� ������� �����:
| || | s11 | || | || | s12 | || | || | s1n | || | |||||||||||
| || | s21 | || | || | s22 | || | || | sn2 | || | |||||||||||
| Y1 | = | || | … | || | , | Y2 | = | || | … | || | , | … | , | Yn | = | || | … | || | . |
| || | sn1 | || | || | sn2 | || | || | snn | || |
�������������, ������ �������
sij ������� S ����
�������� �������� ������� ��������� i-� �������,
������������ ��� ����������� ������� ������� ��������� ��������
j-� �������.
� ������������ � ������������� ������� ������
�������� xi ������ ���� ��������������
��� ��������������� ��������� yi �
aij.
������� � ����������
������������, ���� ��� ������ ������� Y
���������� ������� X ��������� (E — A) X =
Y. � ���� ������ � ������ ��������� ����������
������������.
���������� ��������� ��������� ��������������
������� �. ���� �� ��� ������� � ���, ��� �������
� �����������, ���� �������� ���� ��������� �� �������� ��
����������� �������, ������ ���� �� ��� ������ �� �������� ����� ���������
������ ������ �������.
������ 3.1.
� ������� ��������� ������ �� ���������� ������� ��
�������� ������ � ���. ���. ��.:
| ������� | ����������� | �������� ������� | ������� ������ | ||
| ���������� | �������������� | ||||
| ������������ | ���������� | 7 | 21 | 72 | 100 |
| �������������� | 12 | 15 | 123 | 150 |
��������� ����������� ����� �������� ������� ������
�������, ���� �������� ����������� �������������� ������� ���������� �����,
� �������������� ���������� �� ������� ������.
������� 3.1.
����� x1 = 100,
x2 = 150, x11 = 7,
x12 = 21, x21 = 12,
x22 = 15, y1 = 72,
y2 = 123.
�� ������� aij = xij /
xj ������� ������������ ������ ������:
a11 = 0,07; a12 =
0,14; a21 = 0,12; a22 =
0,10.
�.�. ������� ������ ������
| || | 0,07 | 0,14 | || | ||
| A | = | || | 0,12 | 0,10 | || |
����� ��������������� �������� � ������������� ��������
��������������:
max {0,17 + 0,12; 0,14 + 0,10} = max {0,19;
0,24} = 0,24 < 1.
������� ��� ������ ������� ��������� ��������
Y ����� ����� ����������� ����� �������� �������
X �� ������� X = (E — A)-1
Y.
������� ������� ������ ������ S = (E —
A)-1:
| || | 0,93 | — 0,14 | || | |||
| E — A | = | || | — 0,12 | 0,90 | || | . |
��� ��� |E — A| = 0,8202,
��
| || | 0,90 | 0,14 | || | ||||||
| S | = | | E — A |-1 | = | 1 / 0,8202 | || | 0,12 | 0,93 | || | . |
�� ������� ������ ��������� ��������:
| || | 144 | || | |||
| Y | = | || | 123 | || | . |
����� �� ������� X = (E — A)-1
Y �������� ������ �������� �������:
| || | 0,90 | 0,14 | || | || | 144 | || | = | || | 179,0 | || | ||||
| X | = | 1 / 0,8202 | || | 0,12 | 0,93 | || | || | 123 | || | = | || | 160,5 | || | , |
�.�. ������� ������ � �������������� ������� ����
��������� �� 179,0 ���. ��., � �
������������������ — �� 160,5 ���. ��.
������ 3.2 (��� ����������������
�������).
� ������� ��������� ������ �� ���������� ������� ��
�������� ������, ���. ���. ��.:
| ������� | ����������� | �������� ������� | ������� ������ | ||
| 1 | 2 | ||||
| ������������ | 1 | 100 | 160 | 240 | 500 |
| 2 | 275 | 40 | 85 | 400 |
��������� ����������� ����� �������� ������� ������
�������, ���� �������� ������� ������ ������� ������ ����������� �
2 ����, � ������ ������� — �� 20%.
�����: (945,6; 691,2)’.
����� �� ������ 3.2 ���������� �� ������ mathematics@home.tula.net. ����
��������� ������� �� ������� ��� �� ������ — ���������.
���� ���������� ������ �� ���� — ����������, ����������
������!
� ��������� ��������:
- �������� ������ ������ (������ ������������� ��������);
- ���������������� �������;
- ������ � ����������� ���������� ���������;
- ������ � ������������������ �����.
Предположим, что рассматривается N отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции, произведенной отраслью, идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, за год). Введем следующие обозначения:
Xi – общий (валовой) объем продукции I-ой отрасли (I = 1, 2,… N);
Xij – объем продукции I-ой отрасли, потребляемой J-ой отраслью в процессе производства (I,J = 1, 2,… N);
Yi –объем продукции I-ой отрасли для непроизводственного (личного и общественного) потребления (I = 1, 2,… N).
Указанные величины можно свести в таблицу:
|
Производственное |
Конечный продукт |
Валовой выпуск |
|
X11 X12 …… X1N X21 X22 …… X2N ——————— Xn1 Xn2 …… Xnn |
Y1 Y2 —— YN |
X1 X2 —— XN |
Так как валовой объем продукции любой I-ой отрасли равен суммарному объему продукции, потребляемой всеми N отраслями, и конечного продукта, то должно выполняться соотношение
(I = 1, 2,… N),
Или, в сокращенной форме

Уравнения (3.1) (их N штук) называются Соотношениями межотраслевого баланса. Единицы измерения содержащихся в уравнениях (3.1) величин могут быть натуральными и для каждого уравнения свои (кубометры, тонны, штуки и т. п.). Но они могут быть и универсальными (стоимостными). В зависимости от этого различают Натуральный И Стоимостной межотраслевые балансы. Для определенности рассмотрим далее стоимостной баланс (все величины, входящие в уравнения (3.1), выражены в рублях).
Введем Коэффициенты прямых затрат

Показывающие затраты I-ой отрасли на производство единицы продукции J-ой отрасли. То есть Aij – стоимость продукции отрасли I, вложенной в 1 рубль продукции отрасли J. Так как эти коэффициенты зависят в основном от существующей технологии производства в производящих отраслях, а эта технология меняется достаточно медленно и за рассматриваемый относительно короткий период времени может считаться неизменной, то их можно считать постоянными. Это означает линейную зависимость объема Xij продукции I-ой отрасли, потребляемой J-ой отраслью, от валового объема Xj J-ой отрасли:
(I = 1, 2,… N). (3.3)
Построенная на этом основании модель межотраслевого баланса получила название Линейной, или модели Леонтьева (американский экономист русского происхождения, лауреат Нобелевской премии по экономике).
С учетом линейных соотношений (3.3) равнения межотраслевого баланса (3.1) примут вид:

Введем обозначения:



Где А – так называемая матрица прямых затрат, X – матрица-столбец валового выпуска, Y – матрица-столбец конечного продукта. Тогда систему (3.4) N линейных уравнений с N неизвестными (X1; X2; …Xn) можно записать в матричном виде:
(3.6)
Система (3.6) представляет собой математическую формулировку модели Леонтьева межотраслевого баланса в матричной форме. А задача межотраслевого баланса состоит в отыскании такой матрицы-столбца валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор-столбец конечного продукта Y.
В соответствии с экономическим смыслом задачи искомые элементы столбца X должны быть неотрицательны при любых неотрицательных значениях YI и AIj (I = 1, 2,… N). В таком случае модель Леонтьева называется Продуктивной.
Существует несколько различных по форме Критериев продуктивности модели Леонтьева. Один из них формулируется так (доказательство опускаем): если максимум сумм элементов столбцов матрицы A прямых затрат не превосходит единицы, то есть если

И существует номер J такой, что эта сумма строго меньше единицы

То модель Леонтьева (3.6) (или, что одно и то же, (3.4)) является продуктивной. Отметим, что условия (3.7) и (3.8) естественны, так как они имеют наглядный экономический смысл. Действительно,

– это доля, которую составляет суммарная стоимость продукции всех отраслей, вложенная в продукцию J-ой отрасли, по отношению к общей стоимости продукции J-ой отрасли. И эта доля для любой отрасли, естественно, не должна превосходить единицу. А точнее, для рентабельной отрасли должна быть меньше единицы, ибо общая стоимость Xj продукции J-ой отрасли включает в себя и другие затраты – стоимость рабочей силы, амортизацию основных фондов и т. д., а также прибыль, получаемую отраслью от продажи продукции.
Пример 1. В таблице ниже содержатся данные баланса промышленности и сельского хозяйства в некотором регионе за некоторый период (в миллиардах рублей):
|
Отрасль |
Производственное |
Конечный |
Валовой |
|
|
Промышленность |
Сельское |
|||
|
Промышленность |
0,7 |
2,1 |
7,2 |
10 |
|
Сельское Хозяйство |
1,2 |
1,5 |
12,3 |
15 |
Требуется вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт промышленности увеличится вдвое, а сельского хозяйства останется на прежнем уровне.
Решение. Согласно таблицы имеем:
|
X11 = 0,7; |
X12 = 2,1; |
X21 = 1,2; |
X22 = 1,5; |
|
X1 = 10; |
X2 = 15; |
Y1 = 7,2; |
Y2 = 12,3. |
По формуле (3.2) находим коэффициенты прямых затрат:



Таким образом, матрица А Прямых затрат
Имеет неотрицательные элементы и, очевидно, удовлетворяет критерию продуктивности, выражаемому неравенствами (3.7) и (3.8), ибо
;
.
По условию задачи, в измененных условиях производства конечный продукт промышленности Y1 должен составить млрд. рублей, а конечный продукт Y2 сельского хозяйства должен остаться неизменным и составить 12,3 млрд. рублей. Поэтому для определения соответствующих валовых объемов X1 и X2 этих отраслей получаем, согласно (3.4), следующую систему линейных уравнений 2-го порядка:
Ее главный определитель
Значит, система имеет единственное решение. Вычисляя еще два определителя неизвестных
И используя формулы Крамера (2.5), получим:


| < Предыдущая | Следующая > |
|---|
Задача
Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках
и векторе объемов конечного использования
.
Требуется:
Указание:
При вычислениях производить округление с точностью до тысячных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Матрица прямых затрат
Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора
:
Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя
числовые значения, получаем:
Матрица «Затраты — выпуск»
Найдем матрицу
«Затраты — выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем
матрицу коэффициентов полных материальных затрат
-она будет равна обратной матрице
:
Определитель матрицы
:
Алгебраические
дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска
для конечного продукта
определим формуле:
Приросты валовых объемов выпуска
Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на
по сравнению с
:
Матрица полных затрат ресурсов S
Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем
матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность
матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида. Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.