Содержание:
- Преобразования
- Преобразования плоскости
- Пример с решением
По этой ссылке вы найдёте полный курс лекций по математике:
Преобразования
Преобразования, наделенные таким свойством, позволяют успешно решать задачи аэро- и гидродинамики, теории упругости, теории полей различной природы и многие другие. Мы ограничимся преобразованиями плоских областей. Непрерывное отображение го = /(г) плоской области в область на плоскости называется конформным в точке , если в этой точке оно обладает свойствами постоянства растяжения и сохранения углов.
Открытые области и называются конформно эквивапентными,если существует взаимнооднозначное отображение одной из этих областей на другую, конформное в каждой точке. Теорема Римана. Любые две плоские открытые односвязные области, границы которых состоят более чем из одной точки, конформно эквивалентны. Основной проблемой при решении конкретных задач является построение по заданным плоским областям явного взаимно однозначного конформного отображения одной из них на другую.
Один изспособоврешенияэтой проблемы в плоском случае — привлечение аппарата теории функций комплексного переменного. Какужеотмечалось выше, однолистная аналитическаяфункция с отличной от нуля производной осуществляет конформное отображение своей области задания на ее образ. При построении конформных отображений весьма полезно следующее правило. Принцип соответствия границ.
Пусть в односвязной области Я) комплексной плоскости z, ограниченной контуром 7, задана однозначная аналитическая функция w = f(z), непрерывная в замыкании 9) и отражающая контур 7 на некоторый контур 7′ комплексной п/юскости w. Если при этом сохраняется направления обхода контура, то функция w — f(z) осуществляет конформное отображение области комплексной плоскости z на область З1 комплексной плоскости w, ограниченную контуром 7′ (рис. 1).
Возможно вам будут полезны данные страницы:
Цель настоящего параграфа состоит в том, чтобы, используя найденные ранее области однолистности основных элементарных фуннций комплексного переменного, научиться строить конформные отображения открытых одно-связных плосжх областей, часто встречающихся в приложениях, надвестан- КОНФОРМНЫЕ ОТОБРАЖЕНИЯ дартныс области — верхнюю полуплоскость и единичный круг (рис. 2). Для более эффективного использо- Рис.2 вания приводимой ниже таблицы полезны некоторые простейшие преобразования комплексной плоскости.
Преобразования плоскости
Преобразования плоскости, осуществляющие: 1. параллельный перенос (сдвиг на заданное комплексное число а) (рис. 3), Рис.3 2. поворот (на заданный угол 3. растяжение (fc > 1) ил и сжатие (рис. 5). Тем самым, преобразование вида 0 любой круг можно сделать единичным кругом с центром в нуле (рис. 6), любую полуплоскость можосделать верхней полуплоскостью, любой отрезок прямой можно преобразовать в отрезок [0, 1) вещественной оси (рис. 7), любой луч — в положительный луч вещественной оси (рис. 8). б) Рис. 6 растяжение (им) О перенос в) поворот перенос рас гяжение Рис. 7 перенос поворот Рис.8 в) б) В) 4.
Преобразование плоскости z,
переводящее три различные точки z, zi, z3 в три различныеточт плоскости (рис.9). Рассмотрим пример, показывающий, как пользоваться приведенной ниже табли- цей.
Пример с решением:
Отобразить круг с разрезом по радиусу (рис. 10) взаимно однозначно и конформно на единичный круг с центром в нуле. 4 А. Применяя простейшие преобразования плоскости, приведем заданную область к области, имеющейся в таблице. 1. Переместим центр заданного круга в нулевую точку (см. рис. 11): .
Имеем: круг с разрезом 2. Повернем полученный круг по часовой стрелке на угол (см. рис. 12) . Имеем: круг с разрезом arg 3. Сожмем круг в три раза (см. рис. 13) Имеем: круг с разрезом Таким образом, исходная область приводится к имеющейся в таблице при помощи следующего преобразования Б. 1. Указанная область — круг с разрезом — приведена в таблице под № 30. Функция Жуковского КОНФОРМНЫЕ ОТОБРАЖЕНИЯ преобразует эту область в плоскость с разрезом по отрезку [-1, 5] вещественной оси (рис. 14). 2. Указанная область приведена в таблице под № 22.
Применяя дробно-линейное преобразование преобразуем эту область в плоасость с разрезом по лучу [0, +оо) вещественной оси (рис. 15).
3. Указанная область приведена в таблице под № 6. Извлекая квадратный корень преобразуем эту область в верхнюю полуплоскость Im z6 > 0 (рис. 16). 4. Указанная область приведона в таблице под Ng 11. Применяя дробно- линейное преобразование преобразуем эту область в единичный круге центром в нуле Последовательно выражая z* через z^-i, получим взаимно однозначное и конформное преобразование заданного на комплексной плоскости г круга с разрезом по радиусу на единичный круг комплексной плоек ости tr. р- Конформное отображение заданными областями определяется неоднозначно.
Пример с решением:
Отобразить полукруг (рис.18) взаимно однозначно и конформно на верхнюю полуплоскость Im w > 0. . Дробно-линейное отображение преобразует заданный полукруг в прямой угол 2. Указанная область приведена в таблице под Ne 4 (п = 2). Возводя в квадрат Б. Заданная область приведена в таблице за No 9. Искомое преобразование имеет вид чю- Оба отображения w -заданный полукруг в верхнюю полуплоскость переводит взаимно однозначно и конформно Организация таблицы и правила пользования ею.
Таблица строится последующей схеме: номер по порядку, область <2> на комплексной плоскости zy конформное отображение (прямое w = f(z) и обратное z = g{tu)), область Of на комплексной плоскости w, конформно эквивалентная области Под кажды м номером в приводимой в таблице одной из областей, как правило, является либо верхняя полуплоскость, либо единичный круг с центром в нуле.
Как будет показано в конце параграфа, такая стандартизация удобна для практического использования. Часто приводится только преобразование, сводящее заданную область к ранее рассмотренной. В этом случае дается ссылка на преобразование, переводящее полученную область в стандартную (единичный круг с центром в нуле или верхнюю полуплоскость). Основные элементарные функции.
Таблица Плоскость с разрезом по действительному лучу [О, Плоскость с разрезами Плоскость с разрезом по действительному лучу [0, +ю[ Плоскость с разрезом по отрезку 10, 1] Плоскость с разрезом по действительному лучу (0, +«>( Плоскость с разрезами по действительным лучам J -оо, 0] и (I, +оо[ Плоскость с разрезом по действительному лучу [0, +«>( Плоскость с разрезом по отрезку lu. zi] Плоскость с разрезом по отрезку (О, 1J № 21 1лоскость с разрезами ю лучам, лежащим ia прямой, проходящей через ачало координат по действительным лучам ]-«ю, 0] и (1.
Плоскость с разрезом по действительному лучу (0, +во( Плоскость с разрезом по дуге окружности Ixl — 1, lm z > О Плоскость с разрезом по дуге окруж ности III — I, Re z > О Плоскость с разрезом по действительн ому лучу (0, Плоскость с разрезом no дуге окруж ности Плоскость с разрезом по действительному лучу [С, + со [ № 25 Полуплоскость с разрезами Полуплоскость l с разрезом по отрезку [0, /}
Плоскость с разрезом по действительному лучу [ — I, Полуплоскость с разрезом по отрезку Полуплоскость Im г > О с разрезами по отрезку [0, oi) и мнимому лучу №28 Полуплоскость с разрезом по ду| е окружности по действительным лучам |- по действительным лучам 1 — оо, -Л2] с разрезом по мнимому лучу Круг с разрезами Круг 1 с разрезом по отрезку (1/2, 1J №30 Плоскость с разрезом по отрезку {-1, 5/4] Круг Izl с разрезами по отрезкам (-1. -1/2] и (1/2, 1] № 31
Плоскость с разрезами по отрезиам I -5/4, 5/4] Круг Ijl симметричными разрезами по мнимой оси Круг lie с симметричными разрезами по действительной оси Внешность круга с разрезами Внешность единичного круга I с разрезом по отрезку [1, 2J №33 Внешность единичного круга с разрезом по отрезкам 1-2, -1] и 11, 2) №34 Плоскость с разрезом по отрезку [ -1, 5/4] Плоскость с разрезом по отрезку I — 5/4, 3/4] w = e’^z Внешность единичного круга Izl > 1 с разрезами по отрезкам, являющимися продолжениями его диаметра Внешность единичного круга Iwl > 1 с разрезами по отрезкам, лежащим на действительной оси Полуируг с разрезами -г2
Nfc 36 Круг Iwl с разрезом по отрезку [ -1/4, 1] Полукруг , с разрезом по отрезку (0, i/2) Полукруг , с разрезом по отрезку [//2, /) Круг с разрезами по отрезкам № 37 Полукруг с разрезами по отрезкам [0. al) и [Ы. /). где N? 38 Круг с разрезами по отрезкам 1-1. — угол с разрезами Угол с разрезом по действительному лучу Ах» г — т/4 с началом в точке 1 + / Полуплоскость Im W > 0 с разрезом по мнимому лучу с началом в точке 12/, +/•©( Nf39 Плоскость с разрезами по действительным лучам Угол с разрезом по действительному лучу Arg z — т/л с началом в точке Полоса с разрезами w — с*
Полуплоскость Im с разрезом по дуге окружности иг » с Полоса 0 т с разрезом по мнимому отрезку ( Полуплоскость Im с разрезом по дуге окружности w — е Полоса 0 разрезом по мнимому отрезку fW/2, TiJ N? Полоса Полуплоскость Im w > О с разрезами по мнимым с разрезами по дуге отрезкам [0, al и [Ы, «1, окружности w « t*, КОНФОРМНЫЕ ОТОБРАЖЕНИЯ М43 Полоса Плоскость с разрезом по действительному лучу (0. +«( №44 Полоса с разрезом Полуплоскость Im по действительному с разрезом по мнимому лучу I отрезку [О, /I
Полоса 0 Полоса с разрезом по действительному лучу I №46 Полоса Полоса 0 с разрезом по действительному лучу R №47 Область 1 Полоса 01 Область с удаленным кругом Re Полоса Полуплоскость Im z > О с удаленным круговым сегментом Угол №50 -Ш Полуплоскость Im с удаленным круговым сегментом Полуплоскость Im w > 0 № 51 Полуполоса Полуплоскость Im w > Полуплоскость Im Полуполоса с удаленными полукругами № 53
Полуполоса Полуполоса N? 54 Угол Полуплоскость Im w > 0 с удаленным сектором единичного круга Ne 55 Угол Im z с удаленным полукругом Полуполоса 0 Внешность параболы Полуплоскость Im w Внутренность параболы Полуплоскость Im № 58 Внешность гиперболы Полуплоскость Im w Внутренность правой ветви гиперболы Полуплоскость Iro W > О Внешность эллипса Внешность круга М > I
Лекции:
- Определение и свойства функций
- Переход к полярным координатам
- Компланарные векторы
- Решение задач с применением производной
- Среднее квадратическое отклонение
- Треугольники
- Производная примеры решения
- Гиперболические функции
- Однородные дифференциальные уравнения первого порядка
- Натуральные числа
Онлайн-сервисы
Алгоритмы JavaScript
Введение в анализ
Теория множеств
Математическая логика
Алгебра высказываний
Булевы функции
Теория формального
Логика предикатов
Неформальные и формаль-
ные аксиоматические теории
Теория алгоритмов
Математическая логика и компьютеры
Дискретная математика
Множества и отношения
Группы и кольца
Полукольца и булевы алгебры
Алгебраические системы
Теория графов
Булева алгебра и функции
Конечные автоматы и регулярные языки
Контекстно-свободные языки
Интегральное исчисление
Неопределённый и определённый
Приложения интегралов
Интегралы в физике
Основные интегралы
Вариационное исчисление
Финансовый анализ
Анализ эффективности
Анализ устойчивости
Рыночная активность
Инвестиционная деятельность
Анализ инвестиций
Стоимость компании
Форвардные контракты
Теория вероятностей
Математическая статистика
Теория очередей (СМО)
Аналитическая геометрия
Векторная алгебра
Системы координат
Геометрия на плоскости
Линии 2-го порядка
Инварианты линий
Геометрия в пространстве
Поверхности 2-го порядка
Инварианты поверхностей
Линейная алгебра
Матрицы и операции
Определители
Ранг матрицы
Обратная матрица
Системы уравнений
Функциональные матрицы
Многочленные матрицы
Функции от матриц
Линейные пространства
Подпространства
Линейные отображения
Линейные операторы
Евклидовы пространства
Комплексный анализ
Комплексные числа
Комплексные функции
Функциональные ряды в комплексной области
Особые точки, Вычеты
Операционное исчисление
Дифференциальные уравнения
ДУ первого порядка
ДУ высших порядков
Системы ДУ
Теория устойчивости
Численные методы
Методы алгебры
Методы теории приближений
Методы решения обыкновенных ДУ
Методы решения ДУ в частных производных
Конформные отображения и их свойства
Геометрические свойства конформных отображений
Рассмотрим подробнее геометрические свойства конформных отображений с помощью аналитических функций.
Исследование геометрического смысла модуля и аргумента производной аналитической функции показало, что отображение с помощью аналитической функции является конформным в любой точке аналитичности функции, где выполняется условие
. По определению конформного отображения оно обладает в такой точке свойствами сохранения углов и постоянства растяжения.
Взаимно однозначное в конечной области отображение, т.е. отображение, осуществляемое однолистной функцией, конформное в каждой точке области, называется конформным в области
.
Можно показать, что условие является следствием (необходимым условием) однолистности функции
в
. Действительно, отображение
можно записать в виде, где
(2.32)
Из свойств отображения (2.32), изучаемого в действительном анализе, известно, что условием его взаимной однозначности в является условие
, где
— якобиан отображения, определяемый равенством
Отображение (2.32), удовлетворяющее условию , обладает в
следующими свойствами: переводит внутреннюю точку во внутреннюю, граничную — в граничную.
Для функции , аналитической в
, условие
в силу условий Коши-Римана принимает вид
или, раскрывая определитель, . Это последнее условие означает, что
, так как производная аналитической функции
может быть записана в виде
.
Утверждение 2.15. Отображение с помощью аналитической, однолистной в конечной области функции является конформным в
.
Если функция , аналитическая в
, осуществляет взаимно однозначное отображение, то точки
называются образами точек
, а точки
— прообразами. В силу свойств взаимно однозначного отображения образом области
как открытого множества, состоящего из внутренних точек, является область
, а образом кривой
— границы области
— является кривая
— граница области
.
В теории и практике конформных отображений ставятся и решаются две задачи. Первая задача заключается в нахождении образа данной линии или области при заданном отображении — прямая задача. Вторая — заключается в нахождении функции, осуществляющей отображение данной линии или области на другую заданную линию или область — обратная задача.
При решении прямой задачи учитывается, что образом точки при отображении
является точка
, такая, что
, т.е. результат подстановки значения
в
. Поэтому для нахождения образа множества нужно решить систему, состоящую из двух соотношений. Одно из них задает отображающую функцию
, другое — уравнение линии, если решается задача нахождения образа линии, или неравенство, определяющее множество точек прообраза, если решается задача отображения областей. В обоих случаях процедура решения сводится к исключению переменной
из двух заданных соотношений.
Рассмотрим подробнее задачу отображения линии. Чтобы исключить из заданных соотношений, следует выразить
из первого уравнения и подставить во второе, либо наоборот.
Если уравнение линии задано в параметрической форме: , то, записав уравнение
и подставив его в отображающую функцию
, получим соотношение, содержащее параметр
и связывающее координаты точек, принадлежащих соответствующему образу, т.е. уравнение образа данной линии.
Если линия задана уравнением , что в комплексной форме соответствует равенству
, то в последнее соотношение подставляются
и
, полученные из
, то есть
и
. В результате получаем соотношение
, или после подстановки
. Это соотношение будет искомым уравнением образа.
Таким же методом можно решить задачу отображения области. Для этого в неравенство, определяющее заданную область, следует подставить , полученное из отображающей функции
.
Можно решать эту задачу иначе. Известно, что любая замкнутая кривая разбивает плоскость на две области. По свойству конформного отображения граница области переходит в границу, а любая внутренняя точка во внутреннюю. Поэтому для нахождения образа области достаточно найти образ ее границы, а затем по соответствию пары внутренних точек определить, какая из двух областей, имеющих полученную линию своей границей, является искомой.
Результаты приведенных рассуждений сформулируем в виде правил решения прямой задачи для линии и области соответственно.
Правило 2.4. Для нахождения образа данной линии при отображении необходимо:
1. Записать уравнение линии в параметрической форме или в комплексной форме
.
2. В зависимости от вида уравнения линии, заданного или выбранного в п.1, рассмотреть соответствующий случай:
– если линия задана в параметрической форме, подставить выражение в
. Полученное соотношение
— уравнение образа линии
при отображении
;
– если линия задана в комплексной форме, то выразить из
, то есть
, и найти
. Затем следует подставить
и
в уравнение линии. Полученное соотношение — уравнение образа данной линии.
Правило 2.5. Для нахождения образа данной области следует воспользоваться одним из двух способов.
Первый способ.
1. Записать уравнение границы заданной области.
2. Найти образ границы заданной области по правилу 2.4.
3. Выбрать произвольную внутреннюю точку заданной области и найти ее образ при заданном отображении. Область, которой принадлежит полученная точка, является искомым образом заданной области.
Второй способ.
1. Выразить z из соотношения .
2. Подставить полученное в п.1 выражение в неравенство, определяющее заданную область. Полученное соотношение — искомый образ.
Замечания 2.9
1. На практике при нахождении образов с помощью отображений
и других используются свойства этих отображений, например круговое свойство дробно-линейного отображения или свойство функции
увеличивать углы в
раз.
2. При решении обратной задачи используются свойства простейших отображений и некоторый набор известных отображений — «таблица» отображений.
Далее в лекции рассмотрим отображения с помощью простейших функций.
Линейное отображение на комплексной плоскости
Линейная функция , где
и
— любые комплексные числа,
, определена в
, а если положить
, то в
. Отображение является однолистным в
, что вытекает из равенства
, так как при
из условия
следует
(см. также пример 2.4).
Функция является аналитической в . Исходя из сказанного заключаем, что линейное отображение является конформным всюду в
.
Выясним геометрический смысл линейного отображения на комплексной плоскости. Для этого запишем параметр в показательной форме:
и рассмотрим следующие частные случаи отображения как составляющие:
Первому из этих отображений соответствует изменение длины радиуса-вектора любой точки в раз, а именно растяжение, если
, и сжатие при
. Это следует из соотношений
.
Для второго отображения из соотношений получаем, что оно определяет преобразование поворота — радиус-вектор любой точки
поворачивается относительно начала координат на угол а по часовой стрелке, если
, и против — если
.
Геометрический смысл отображения получается из геометрического смысла сложения комплексных чисел, как векторов, или, что то же, из соотношений
. Отображение
есть параллельный перенос радиуса-вектора любой точки
в направлении вектора
на его величину.
На рис. 2.18 проиллюстрированы операции, соответствующие всем рассмотренным отображениям; для наглядности все плоскости совмещены (совмещены их действительные и мнимые оси).
Представляя линейное отображение как суперпозицию рассмотренных отображений, можно сформулировать утверждение.
Утверждение 2.16
1. Отображение геометрически сводится к последовательному выполнению над радиусом-вектором любой точки плоскости z следующих операций: растяжению (сжатию) в
раз, повороту на угол
и смещению (параллельному переносу) в направлении вектора
на величину
.
2. Отображение изменяет линейные размеры любой фигуры плоскости в
раз (гомотетия — подобие с центром в начале координат и коэффициентом подобия
), поворачивает эту фигуру на угол
вокруг начала координат и смещает ее в направлении вектора
на его величину (рис. 2.19).
3. Линейное отображение обладает круговым свойством, т.е. переводит окружности плоскости в окружности плоскости
(и обратно); прямые переводит в прямые.
Справедливость последнего утверждения следует из геометрических свойств составляющих, так как они, очевидно, обладают круговым свойством. Оно также может быть доказано аналитически.
А именно запишем в комплексной форме уравнение прообраза — окружности в плоскости (см. пример 1.27):
и подставим в него выражение для , полученное из
, то есть
. Будем иметь
или после преобразований: , где
. А это и есть уравнение окружности в плоскости
.
При и прообраз, и образ определяют прямые.
Заметим, что доказательство можно рассматривать как пример решения прямой задачи — найти образ окружности (прямой) при линейном отображении и убедиться, что это — окружность (прямая) (см. правило 2.4).
Если использовать уравнение прообраза в виде (см. правило 2.4), после подстановки
получим
, т.е. образом центра данной окружности при линейном отображении является центр
её образа — центр отображается в центр.
▼ Примеры 2.54-2.62 задач на линейные отображения
Пример 2.54. Найти образ отрезка , где
, при отображении
(рис. 2.20).
Решение
Пример 2.55. Найти образ окружности при отображении
.
Решение
Пример 2.56. Найти образ окружности: a) ; б)
при отображении
.
Решение
Пример 2.57. Найти образ оси при отображении
.
Решение
Первый способ. Решаем по правилу 2.4. Уравнение оси выберем в параметрической форме.
1. Так как в действительной форме уравнение имеет вид , то в комплексной форме запишется как
. Это — параметрическое уравнение, в качестве параметра выбран
.
2. Выражаем из
и подставляем в уравнение оси
или, что о же, подставляем
в выражение
. Получаем уравнение образа в параметрической форме:
; параметром является
. Отделив действительную и мнимую части, получим уравнение в действительной норме:
или
. Это есть уравнение прямой в плоскости
, параллельной действительной оси.
Второй способ. Решаем по правилу 2.4, но уравнение оси выберем в комплексной форме.
1. Записываем комплексное уравнение оси .
2. Выражаем из
и подставляем
и
в уравнение
. Получаем в комплексной форме уравнение образа оси
, или
. В действительной форме результат записывается в виде
или
.
Третий способ. Используем для решения круговое свойство линейного отображения — образом прямой является прямая. Так как прямая определяется двумя точками, то достаточно на оси выбрать любые две точки и найти их образы. Прямая, проходящая через найденные точки, и будет искомой. Выберем точки
, их образы
при отображении лежат на прямой
. Следовательно, образом прямой
является прямая
.
Четвертый способ. Можно привести геометрическое решение, как и в примере 2.54. Так как из условия следует, что
, то нужно заданную линию (ось
) повернуть на
(относительно начала координат), а затем сместить вниз на 3 единицы. Растяжение в 2 раза не меняет геометрического вида исходной линии (оси
), так как она проходит через начало координат.
Пример 2.58. Найти какую-либо линейную функцию, отображающую линию на линию
.
Решение
Поставленная задача есть обратная задача теории отображений — по заданным образу и прообразу найти соответствующее отображение. Без дополнительных условий задача не имеет единственного решения. Действительно, существует множество функций, осуществляющих искомое отображение. Для нахождения любой из них достаточно выбрать две точки и
в плоскости
, принадлежащие прообразу (т.е. линии
), и две любые точки
и
в плоскости
, принадлежащие линии
(т.е. два действительных числа), и из двух соотношений
и
определить величины
и
.
Одно из отображений можно просто получить из рассмотрения рис. 2.22.
Для геометрического решения достаточно повернуть луч , принадлежащий прообразу, на угол
против часовой стрелки, т.е. выбрать отображение
. При этом образом точки
будет точка
, а образом точки
— точка
. Можно выбрать отображение
— поворот на угол
по часовой стрелке. Тогда точке
будет соответствовать точка
, а точка
будет образом точки
.
Заметим, что ответом может быть также , где
— любое положительное число, и
, где
и
— любые действительные числа.
Пример 2.59. Найти какую-либо линейную функцию, отображающую окружность на окружность
.
Решение
Как и предыдущая, это — обратная задача отображений. Решать её будем, используя свойства линейного отображения — геометрический смысл его составляющих. В связи с этим при решении удобно выделить следующие этапы (см. рис. 2.23).
Первый этап. Переместим центр окружности в начало координат. Для .того применим отображение .
Второй этап. В плоскости применим отображение, дающее растяжение в 2 раза,
. Окружность изображена в плоскости
(считаем плоскости
и
совмещенными) пунктиром.
Третий этап. Окончательный результат получаем, применяя преобразование смещения, , то есть
или
.
Здесь, как и в примере 2.58, ответ не единственный и можно рассмотреть другой порядок выполнения операций. Из геометрических соображений ясно, что можно сначала применить не смещение, а поворот или растяжение и получить в результате соответствующее отображение.
Можно получить общий вид линейной функции, осуществляющей заданное отображение, используя тот факт, что окружность определяется положением центра и величиной радиуса, и свойство линейного отображения, переводящего центр окружности в центр.
Поэтому, подбирая искомое отображение в виде , из соотношения
, то есть
, получаем
или
. Далее из
, учитывая условие задачи, находим
и
, где
— любое действительное число.
Окончательный результат , что также объяснимо из рис. 2.23, так как геометрический вид окружности с центром в начале координат (см.
или пунктир в плоскости
) не изменяется в результате поворота (умножения на
).
Пример 2.60. Найти образ полосы при отображена
.
Решение
Заданная область — неограниченная односвязная область, границей её на является линия, состоящая из двух параллельных прямых (образами эти: прямых на сфере Римана являются две окружности, пересекающиеся в точке
. Эта линия делит
на две области — внутреннюю (полоса) и внешнюю (внешность полосы).
Образом полосы является полоса, так как при линейном отображение прямые переходят в прямые, а в силу конформности отображения параллельность прямых сохраняется.
Решаем по правилу 2.5 первым способом.
1. Границу области образуют две прямые с уравнениями и
.
2. Находим образы прямых и
. Образ прямой
получен в примере 2.57. Его уравнение
. Образ прямой
можно получить так же или, учитывая параллельность линий, достаточно найти образ одной точки. Например, точке
соответствует
. Поэтому o6pазом прямой
будет прямая
, проходяшая через точку
.
3. Выбираем внутреннюю точку полосы , например
, её oбраз
. Эта точка должна принадлежать искомому образу. Ответом является множество
— полоса, границами которой являются
и
(рис. 2.24).
Очень простое решение задачи — геометрическое, которое сводится к повороту на против часовой стрелки, растяжению в два раза и смешению вниз мнимой оси на 3 единицы (рис. 2.24).
Пример 2.61. Найти линейную функцию, отображающую область на область
.
Решение
По свойствам искомого отображения как взаимно однозначного отображения граница области , прямая
, переходит в границу области
. Функция, устанавливающая соответствие границ, получена в примере 2.58. Это — либо
, либо
,
. Одна из них отображает область
на
(а
соответственно на
), другая — область
на
. Чтобы выбрать необходимую функцию, достаточно установить соответствие двух пар граничных точек или пары внутренних.
Выберем две граничные точки области — точки
и
(см. рис. 2.22, решение примера 2.58). Направление обхода границы области
от точки
к точке
(область при обходе расположена слева), области
— от точки
к точке
. Поэтому искомая функция — та, которая переводит точку
в точку
, то есть
,
или, в частности,
(см. пример 2.58). Можно выбрать внутреннюю точку, .например
. Ее образом при отображении
,
является
, то есть
.
При отображении же ,
образом точки
является
,
.
Пример 2.62. Найти какую-либо линейную функцию, отображающую область на область
.
Решение
Как и в предыдущем примере, нужно найти функцию, устанавливающую соответствие границ: прямой в плоскости
и прямой
в плоскости
(рис. 2.25,а и г).
Применим геометрический способ решения (см. пример 2.59), используя геометрические свойства составляющих.
Первый этап. Сдвинем границу области на единицу влево, т.е. рассмотрим отображение
. Образом области
будет область
(рис. 2.25,б).
Второй этап. Повернем границу области на угол
по часовой стрелке, т.е. рассмотрим отображение
. Образом области
будет область
(рис. 2.25,в).
Третий этап. Сдвинем границу области на единицу вниз, т.е. рассмотрим отображение
. Образом области
будет область
. Искомое отображение получим как суперпозицию составляющих, т.е.
Напомним, что задачи такого типа без дополнительных условий имеют неединственное решение, что в данном случае очевидно из рассмотрения рис. 2.25.
Например, решением будет также функция и др.
Дробно-линейное отображение на комплексной плоскости
Дробно-линейным называется отображение с помощью функции , где
— произвольные комплексные числа (параметры).
Полагаем , так как при
получается рассмотренная выше линейная функция, и
, иначе, в силу пропорциональности числителя и знаменателя,
.
Функция определена в . Если положить
и
, то получаем функцию, которая определена на всей расширенной комплексной плоскости
.
Функция является однолистной в и аналитической в
за исключением точки
. Аналитичность
следует из определения, так как аналитической в
является функция
.
Так как однолистное отображение с помощью аналитической функции является конформным, то заключаем, что дробно-линейное отображение конформно в , конформно в любой области
. Заметим, что
для любой точки
.
Геометрические свойства дробно-линейного отображения
Исследуем геометрические свойства дробно-линейного отображения. Как и в случае линейной функции, выделим составляющие. Выделяя целую часть дроби, получаем или, вводя обозначения
, имеем
, из чего следует, что дробно-линейное отображение есть суперпозиция линейного отображения и отображения
. Действительно, можно записать цепочку составляющих
Рассмотрим отдельно отображение как частный случай дробно-линейного отображения
. Его также можно записать в виде более простых для исследования составляющих
. Особенность первого отображения заключается в соотношениях
, которые, учитывая, что
и
, можно переписать в виде
(2.33)
Геометрически эти соотношения означают, что точки и
расположены на одном луче, а произведение длин их радиусов-векторов равно единице. Точки, обладающие таким свойством, называются точками, симметричными (или сопряженными) относительно окружности единичного радиуса с центром в начале координат.
Функция отображает любую точку, лежащую внутри единичного круга, в точку, лежащую вне единичного круга, так как из
следует
и обратно.
Следовательно, функция переводит внутренность единичного круга во внешность и наоборот. Преобразование такого вида называется инверсией относительно единичной окружности.
Заметим, что для построения точки по заданной точке
нужно сначала провести луч из центра окружности
, а затем к этому лучу в точке
восставить перпендикуляр и провести касательную к окружности в точке её пересечения с перпендикуляром. Точкой пересечения касательной и луча будет
. Обоснование построения следует из рассмотрения подобных треугольников (рис. 2.26). Очевидно, проводя построение в обратном порядке, можно построить по точке, лежащей вне круга (на рис. 2.26 точка
), симметричную относительно окружности точку
, которая будет расположена внутри круга.
Вторая составляющая отображения функция
геометрически есть симметрия относительно действительной оси (рис. 2.26).
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 2.17
1. Отображение геометрически сводится к построению инверсии относительно окружности
и симметрии относительно действительной оси.
2. Дробно-линейное отображение геометрически сводится к преобразованиям растяжения, поворота, сдвига (см. линейное отображение), симметрии относительно окружности и симметрии относительно действительной оси.
Круговое свойство дробно-линейного отображения
Дробно-линейное отображение на комплексной плоскости обладает круговым свойством. Достаточно доказать это свойство для функции , так как для линейных составляющих дробно-линейного отображения оно установлено.
Доказательство проведем в соответствии с правилом 2.4 решения прямой задачи.
1. Записываем уравнение произвольной окружности в комплексной форме: . Заметим, что при
уравнение определяет прямую. При
линия не проходит через начало координат (точку
), при
— проходит.
2. Выражая из
, получаем
и подставляем в уравнение прообраза. Преобразуем полученное равенство:
, или
.
Полученное уравнение есть уравнение окружности, в частности, при — прямая.
Для отображения роль точки
, очевидно, играет
.
Утверждение 2.18 (круговое свойство дробно-линейного отображения).
1. Окружности и прямые, не проходящие через особую точку , отображаются в окружности, а окружности и прямые, проходящие через эту точку, — в прямые.
2. Дробно-линейное отображение переводит окружности расширенной комплексной плоскости в окружности , так как прямые на расширенной комплексной плоскости рассматриваются как окружности.
▼ Примеры 2.63-2.68 задач на дробно-линейные отображения
Пример 2.63. При отображении найти образы:
а) окружностей и
;
б) прямых и
.
Решение
а) Первая окружность проходит через точку — особую точку функции, поэтому её образом будет прямая. Образом второй окружности, уравнение которой можно переписать как
, является окружность. Решаем согласно правилу 2.4.
1. Записываем уравнения окружностей в комплексной форме: и
.
2. Подставляем в эти уравнения выражения и
Для первой окружности получаем
, или
, что можно записать
, или
. Это — уравнение прямой, параллельной мнимой оси (рис. 2.21,а). Для второй окружности имеем
. Наличие слагаемого
говорит о том, что образом является окружность. Чтобы определить её центр и радиус, перейдем к действительной форме уравнения, используя равенства
. Получим уравнение
, или, выделив полный квадрат переменной
. Это — уравнение окружности радиуса
с центром в точке
(рис. 2.21,а).
б) Образом первой прямой является окружность, второй — прямая. Чтобы получить уравнения соответствующих образов, подставим и
в уравнения данных линий, записанных в комплексной форме:
и
. Получим
— образ первой прямой и
— второй. Первая линия — окружность
или
; её радиус
, центр в точке
(рис. 2.27,6). Уравнение
или
определяет мнимую ось (рис. 2.21,б).
Пример 2.64. Найти образ полосы при отображении
.
Решение
Пример 2.65. Найти образ области при отображении
.
Решение
Область есть пересечение полуплоскости и внешности круга — полуплоскость
с выброшенным кругом (рис. 2.28).
В соответствии с правилом 2.5 решения задач для областей, как и в предыдущем примере, найдем прежде образ границы области , которая состоит из двух линий, описываемых уравнениями
и
. Так как обе линии проходят через особую точку
, то их образами будут прямые. Для каждой линии решаем задачу по правилу 2.4.
Найдем образ прямой .
1. Запишем уравнение в комплексной форме:
.
2. Выражаем из
, то есть
. Подставляем эти значения в уравнение
. Получаем
, или
. Это уравнение определяет прямую
, параллельную действительной оси (рис. 2.28).
Найдем образ окружности .
1. Запишем уравнение окружности в виде .
2. Выразим из
и подставим
в уравнение
. Получаем
. Это равенство определяет уравнение прямой, проходящей перпендикулярно отрезку, соединяющему точки
и
, через его середину. Этой прямой является действительная ось
(рис. 2.28). В результате получили, что образ границы области
состоит из двух параллельных прямых:
и
.
Далее в соответствии с п.3 правила 2.5 выберем произвольную точку, например . Так как ее образом при заданном отображении является
, то образом области
будет полоса
.
Пример 2.66. Найти какую-либо дробно-линейную функцию, отображающую круг единичного радиуса с центром в начале координат:
а) на левую полуплоскость;
б) на нижнюю полуплоскость.
Решение
Решается обратная задача отображения областей. Требуется найти отображение области на область
a)
; б)
. Границей области
является окружность
. Так как в обоих случаях ее образ — прямая, то, согласно утверждению 2.18, искомая функция должна иметь особой точкой одну из точек окружности — окружность проходит через особую точку.
Используя это свойство, «распрямим» окружность, т.е. на первом этапе решения подберем функцию, переводящую одну из точек окружности в бесконечно удаленную точку.
Первый этап. Рассмотрим , где
при
.
Найдем уравнение прямой, в которую переходит при отображении
, т.е. решим прямую задачу:
. Получено уравнение прямой, проходящей перпендикулярно отрезку, соединяющему точки
и
, через его середину, т.е.
. Образом области
будет
, так как, например, точка
переходит в точку
.
Второй этап. Сравнивая полученный результат и вид области , заключаем, что нужно применить преобразование смещения (сдвиг) влево на
, т.е. линейное отображение
. Образом
будет
. Соответствие границ установлено функцией
или
. Но при этом отображении образом области
является правая полуплоскость
, так как точка
, принадлежащая
, переходит в точку
.
Третий этап. Чтобы получить искомое отображение и для случая «а» , и для случая «б», достаточно сделать поворот.
Решим задачу для случая «а». Применим преобразование поворота на угол против часовой стрелки, т.е. линейное отображение
(2.34)
Таким образом, найдено отображение, переводящее круг на полуплоскость
(рис. 2.29).
Заметим, что в силу взаимной однозначности обратная функция отображает левую полуплоскость
на крут
. Отсюда следует вид отображения, переводящего левую полуплоскость
на круг
(рис. 2.30):
(2.35)
Решим задачу для случая «б». Чтобы получить отображение круга на нижнюю полуплоскость
(рис. 2.31), достаточно в плоскости
рассмотреть поворот на
, по часовой стрелке, т.е.
(2.36)
Пример 2.67. Отобразить область на область
.
Решение
Так как образами окружностей — границы области являются прямые, то нужно применить отображение, «распрямляющее» прямые. Для этого следует использовать отображение, переводящее общую точку окружностей
в
.
Первый этап. Применяем преобразование .
Найдем образ области при этом отображении. Для этого, как и при решении предыдущих примеров, в уравнения границы — окружностей
и
подставляем
, то есть
или
.
Эти уравнения определяют прямые, уравнения которых в действительной форме имеют вид и
, или
. Эти прямые, параллельные мнимой оси, определяют границу области
; область
— внутренность полосы, так как, например, образом точки
является точка
, принадлежащая полосе (рис. 2.32).
Второй этап. Сравнивая вид областей и
, убеждаемся, что следует увеличить ширину области
в 4 раза и повернуть ее на угол
против часовой стрелки, т.е. применить преобразование
. Образом
будет полоса
.
Третий этап. Окончательный результат получаем смещением на единиц влево, , то есть
.
Пример 2.68. При отображении, полученном в примере 2.67, найти образы прямых .
Решение
Примеры 2.67 и 2.68 иллюстрируют круговое свойство отображения у свойство конформности. Так, прямая касается окружностей в плоскости
и параллельна прямой
, т.е. образует с каждой из них угол
. Её образ в плоскости
с соответствующими линиями также образует угол
.
Прямая перпендикулярна любой из рассматриваемых здесь линий — и прямым
, и окружностям, так как проходит через их центры. Образ этой прямой (действительная ось
) также перпендикулярен соответствующим линиям — трем прямым и окружности.
Прямая образует угол
с окружностью
1 и прямой
, а с другой окружностью
и прямой
— угол
. Такие же углы образует окружность — образ этой прямой в плоскости
с соответствующими линиями.
Условия, определяющие дробно-линейное отображение
Дробно-линейное отображение рассматривается, как отмечено выше, при , поэтому можно записать
или
,
т.е. оно определяется тремя параметрами. Следовательно, для задания дробно-линейного отображения достаточно задать три условия, например соответствие трех пар точек. При этом, так как отображение рассматривается на , одна из точек может быть бесконечно удаленной. Имеет место утверждение.
Утверждение 2.19 (условия, определяющие дробно-линейное отображение). Каковы бы ни были три различные точки , плоскости
и три различные точки
плоскости
, существует единственное дробно-линейное отображение
такое, что
. При этом справедливо соотношение
(2.37)
Равенство (2.37) называется ангармоническим отношением. Если его переписать в виде произведения:
(2.38)
то, рассматривая предельный переход в (2.38) при или
, замечаем, что предел частного, содержащего соответствующие величины, равен единице. Например,
. Можно сделать заключение.
Если одна из точек или
есть бесконечно удаленная точка, то в (2.37) (или (2.38)) соответствующая разность заменяется единицей.
Справедливость утверждения о единственности отображения, определяемого указанными условиями, и справедливость отношения (2.37) могут быть установлены из рассмотрения линейной системы или
.
Отметим некоторые особенности отображения (2.37), запишем их в виде утверждения.
Утверждение 2.20
1. Дробно — линейное отображение переводит круг, граница которого проходит через три данные точки , в круг (или во внешность круга), граница которого проходит через три точки
. Это следует из того, что положение любой окружности (на плоскости) однозначно определяется тремя точками.
2. Любое дробно-линейное отображение, переводящее точку в ноль и
в бесконечно удаленную точку, имеет вид (что следует из формулы (2.38))
(2.39)
С учетом этого утверждения можно сократить процедуру решения примера 2.66. А именно, так как граница области — прямая
проходит через
, то, полагая
, отображение ищем в виде
(на первом этапе). Можно взять
, так как наличие множителя
в таких случаях будет определять только поворот на
, a растяжение в
для геометрического положения прямых, проходящих через начало координат, не имеет значения. Далее, для решения задачи в случае «а» убеждаемся, что искомое отображение уже получено:
, а для решения в случае «б» нужно ещё сделать поворот.
Пример 2.69. Найти дробно-линейную функцию , такую, что
.
Решение
В утверждении 2.20 сказано, что дробно-линейное отображение переводит любой круг (внутренность, внешность) на любой круг (внутренность, внешность) заданием соответствия трех пар граничных точек. Так как прямые на рассматриваются как окружности
, то речь здесь идет и о прямых, т.е. любой круг (внутренность, внешность) переводится на любую полуплоскость и обратно заданием соответствия трех граничных пар (для прямой одна из точек
).
По формуле (2.38) при условии будет получено определенное отображение области
(ее граница — окружность, прямая) на область
(граница — окружность, прямая). При этом любой внутренней точке
будет соответствовать определенная
.
Сохранение симметричных точек дробно-линейным отображением
Представляют практический интерес задачи, где образом данной точки должна быть заранее заданная
.
Задание соответствия внутренних точек накладывает ограничение на выбор других соответствующих пар. Это связано со следующим свойством дробно-линейного отображения.
Утверждение 2.21
1. Дробно-линейное отображение переводит любые две точки, симметричные относительно окружности расширенной комплексной плоскости, в точки, симметричные относительно образа этой окружности при данном отображении. Свойство называется свойством сохранения симметричных точек.
2. Точки, симметричные границе области (окружности или прямой) при дробно-линейном отображении, переходят в точки, симметричные относительно ее образа при этом отображении.
Свойство означает, что если точки и
симметричны относительно линии у (окружности или прямой) в плоскости
, а точки
и
и линия
— их образы при дробно-линейном отображении, то точки
и
симметричны относительно
. Линия
, согласно круговому свойству отображения, также является окружностью или прямой. Симметрия точек относительно прямой понимается в обычном смысле. Симметрия относительно окружности единичного радиуса с центром в начале координат рассматривалась при исследовании отображения
(формула (2.33)). В общем случае имеет место следующее определение.
Точки и
называются симметричными (или сопряженными) относительно окружности
, если они лежат на одном луче, выходящем из центра окружности, и произведение их расстояний от центра окружности равно квадрату ее радиуса, т.е. справедливо равенство
(2.40)
Точкой, симметричной точке — центру окружности, очевидно, является бесконечно удаленная точка.
Полученные при решении примера 2.71 (см. ниже в спойлере) результаты запишем в виде утверждения.
Утверждение 2.22
1. Любое дробно-линейное отображение полуплоскости на круг
имеет вид
(2.41)
2. Любое дробно-линейное отображение круга на круг
имеет вид
(2.42)
3. Значение а определяется из дополнительного условия. Это, как правило, задание аргумента производной искомой функции в некоторой точке, например .
Формулы (2.41) и (2.42) дают решение двух канонических задач. Для удобства использования изобразим их на рис. 2.34 и рис. 2.35 соответственно.
▼ Примеры 2.70-2.73 решения задач с отображениями
Пример 2.70. Отобразить область на область
так, чтобы точки 0 и 2i остались неподвижными.
Решение
Задание неподвижной точки для отображения
означает условие
, то есть
В данном случае имеет место соответствие двух пар точек:
, причем первая пара — пара граничных точек, вторая -внутренних. Третью пару, необходимую для применения формулы (2.37), находим, используя свойство сохранения симметричных точек.
Найдем точки, симметричные точкам и
относительно соответствующих окружностей.
Для точки точкой, симметричной относительно окружности
, будет
, так как
— центр круга. Для точки
точку, симметричную относительно окружности
, находим, используя формулу (2.40),
, или
. Из полученного равенства следует, что
расположена на расстоянии
от центра круга
и, по определению симметричных точек , на одном луче с центром и точкой
. Из этих рассуждений очевидно, что
. Таким образом, имеем соответствие трех пар точек:
.
Применяя формулу (2.37), получаем , или после преобразований
.
Пример 2.71. Отобразить область на круг
так, чтобы
, если: a)
; б)
.
Решение
Так как точка отображается в
, т.е. в центр круга
, то точка
, сопряженная точке
относительно границы области
, отображается в
. Имеем соответствие двух пар точек, причем
и
. Можем искать отображение в виде
(см. (2.39)). Нужно найти величины
и
.
1. Найдем — точку, симметричную точке го относительно границы области
в каждом случае:
а) так как граница области — действительная ось, то
;
б) здесь симметрична точке
относительно окружности
, поэтому
(см. (2.33)).
2. Значение определяем из соответствия граничных точек:
, где
. Так как
, то получаем условие для нахождения
.
Получим решение для каждого из рассматриваемых случаев.
а) Имеем . Так как
, то
— действительное число и поэтому
. Получаем
и
. Искомое отображение
, где
— любое число.
Заметим, что неоднозначность ответа, вызванная произволом выбора а, связана с неопределенностью соответствия . Указана принадлежность этих точек границам соответствующих областей, но не заданы определенные значения. Каждому фиксированному значению
можно поставить в соответствие произвольное значение
, удовлетворяющее условию
. Отображение найдено с точностью до поворота окружности
, что геометрически очевидно. При задании дополнительного условия для нахождения
решение поставленной задачи единственное.
б) Отображение ищем в виде , то есть
, или, если обозначить
, то
.
Из условия для
получаем
.
Так как для
, то, подставляя
, перепишем равенство
, или
.
В последнем равенстве как модули комплексных сопряженных чисел и
. Поэтому
и
.
Искомое отображение . Как и в предыдущем случае, оно не является единственным.
Пример 2.72. Отобразить область на
так, чтобы выполнялись условия
.
Решение
По условию точка отображается в
, следовательно, точка
, симметричная точке
относительно прямой
, отображается в центр окружности
, т.е. в точку
(рис. 2.36,а).
Задача, очевидно, эквивалентна задаче нахождения отображения полуплоскости на круг
, при условии, что данная точка
полуплоскости переходит в центр круга (незаштрихованная область на рис. 2.36,а).
Эта задача отображения полуплоскости на круг может быть приведена к канонической. Но чтобы воспользоваться формулой (2.41), нужно применить предварительно два линейных отображения, переводящих область в верхнюю полуплоскость, а круг
в единичный круг с центром в начале координат (рис. 2.36,б).
Первый этап. Первое из этих преобразований — поворот на угол по часовой стрелке осуществляется функцией
при этом точка
переходит в
.
Для второго преобразования используем функцию — смещение и сжатие; при этом центр круга перейдет в
.
Второй этап. Для переменных и
используем формулу (2.41), т.е. запишем
, или после сокращения на
.
Полученная функция при любом осуществляет отображение
на
, при этом
.
Третий этап. Для определения параметра используем условие
. Находим производную
и ее значение в точке
, то есть
.
По правилу нахождения аргумента произведения комплексных чисел из последнего равенства получаем , то есть
. Из этого равенства и условия
находим
. Подставляя
в полученное выше выражение, находим окончательный результат:
, или
. Искомое отображение
.
Пример 2.73. Найти образ прямой при отображении, полученном в примере 2.72.
Решение
Заметим, что данная прямая перпендикулярна границе области из примера 2.72, поэтому, по свойству отображения ее образ — линия, перпендикулярная окружности
. Кроме того, так как данная прямая не проходит через особую точку функции, то, по круговому свойству, ее образом будет окружность. Эта окружность ортогональна окружности
в точке их пересечения. Найдем ее уравнение. Решается прямая задача по правилу 2.4.
1. Запишем уравнение линии в форме
, или после преобразований:
.
2. Из выражаем
, получаем
. Подставляем
и
в уравнение и преобразуем равенство
Полученное уравнение — уравнение окружности, так как в нем присутствует слагаемое . Запишем это уравнение в действительной форме:
, или
, где
.
Центр окружности в точке (2,1), радиус равен 2 (рис. 2.37).
Заметим, что эта окружность пересекает окружность из примера 2.72 под прямым углом, так как касательная к одной совпадает с радиусом другой и наоборот. Под прямым углом пересекаются и их прообразы (рис. 2.37), что иллюстрирует конформность отображения в точке .
Отображение степенной функции на комплексной плоскости
Рассмотрим пример не всюду конформного отображения с помощью функции, которая не является однолистной в . Ранее исследовалась такая функция :
(степенная функция), в частности
. Напомним полученные результаты.
Утверждение 2.23
1. Отображение неоднолистно в
; областью однолистности является любая область, принадлежащая углу раствора
(сектору), т.е.
, где
— любое.
2. Функция , аналитическая в
и
, то есть
для любого
. Отображение является конформным в
, за исключением, быть может, точки
.
3. Функция конформно и взаимно однозначно отображает любой сектор
на плоскость с разрезом по лучу
, а плоскость
с выброшенной точкой
— на риманову поверхность этой функции.
4. Функция — обратная к неоднолистной (n-листной) функции
является неоднозначной (n-значной). В областях, не содержащих точек
и
(точек ветвления функции), возможно выделение однозначных ветвей. Каждая ветвь отображает плоскость с разрезом
на один из секторов
. Риманову поверхность функции
функция
отображает на
с выброшенной точкой.
Выясним геометрические свойства отображения в точке . Запишем переменные в показательной форме:
и из равенства
получим:
, или
и
. При отображении
увеличивается в
раз аргумент — угол наклона радиуса-вектора точки к действительной оси, а при отображении
— уменьшается в
раз. Можно сделать заключение.
Утверждение 2.24
1. При отображении увеличиваются в
раз углы между любыми прямыми, проходящими через начало координат. Поэтому отображением
пользуются, если нужно увеличить углы при переходе от прообраза к образу.
2. При отображении уменьшаются в
раз углы между любыми прямыми, проходящими через начало координат. Поэтому отображением
пользуются, если нужно уменьшить углы при переходе от прообраза к образу.
3. Используя комбинацию дробно-линейного отображения и отображений и
, можно конформно отобразить любую «луночку» — область, ограниченную двумя дугами пересекающихся окружностей, на верхнюю полуплоскость.
▼ Примеры 2.74-2.78 задач со степенными отображениями
Пример 2.74. При отображении найти образ области, ограниченной двумя лучами, выходящими из начала координат и образующими угол
.
Решение
Область есть угол раствора
, и при отображении
переходит в угол раствора
. Границами области
являются лучи
и
, их параметрические уравнения имеют вид
и
, где
— любое,
— параметр.
Образами этих прямых будут прямые-лучи и
или
и
, где
. Геометрически линии совпадают. Для однозначности отображения на границе проводим разрез по лучу
(рис. 2.38). Образом области
является плоскость с разрезом получу
; угол
отображается в угол
.
Заметим, что этот же результат получается и для каждого из трех других углов, образованных продолжением выбранных лучей за начало координат (рис. 2.38). Так, для области , имеем
и поэтому
или
, где
совпадает геометрически с
.
Для области из
получаем
, или
и
совпадает геометрически с
.
Наконец, для из
получаем
и
и
совпадает геометрически с
.
В частности, при область
определяется условием
— первый квадрант;
— другие квадранты. Все эти области функцией
отображаются на плоскость с разрезом по лучу
(рис. 2.39).
При соответствующие области отображаются на плоскость с разрезом по лучу
(рис. 2.40).
Пример 2.75. Отобразить «луночку» на верхнюю полуплоскости.
Решение
Границу «луночки» образуют дуги двух окружностей, пересекающихся t точках и
под углом
, а границу ее образа — два луча, образующие действительную ось, угол между ними равен
(рис. 2.41).
Так как нужно увеличить угол вдвое, применим отображение . Но прежде надо «распрямить» дугу, т.е. применить преобразование, переводящее все окружности в прямые. Для этого достаточно, чтобы одна из их общих точек отображалась в бесконечно удаленную точку (см. пример 2.67).
Первый этап. Применяем дробно-линейное преобразование , где, например,
, то есть переводим 0 в 0
в
.
Образами дуг при отображении будут два луча, пересекающиеся в начале координат под прямым углом. Положение лучей (наклон) определяется параметром
.
Для определенности отображения на этом этапе зададим значение или найдем его, задав третью пару — соответствие внутренних точек. Из соображений симметрии удобно взять, например,
. Образом точки
, принадлежащей луночке , будет точка
, принадлежащая первая квадранту.
Из равенства находим
и получаем отображение
.
Образом «луночки» будет первый квадрант, а образами дуг — действительная и мнимая полуоси, так как из соответствия и
следует, что образом прямой, соединяющей точки
и
, будет биссектриса первого координатного угла в плоскости
.
Второй этап. Применяем преобразование , удваивающее углы, и получаем окончательный ответ:
или
.
Пример 2.76. Отобразить полукруг на верхнюю полуплоскость.
Решение
Рассуждая, как и в предыдущем примере, замечаем, что нужно прежде «распрямить» окружность; при этом образом прямой должна быть также прямая. Поэтому нужно взять преобразование, переводящее одну из точек пересечения дуги и прямой в бесконечность.
Первый этап. Пусть (на рис. 2.42,а точки
и
) , т.е. выбираем отображение
. При
это
и
при
.
Второй этап. Определим образ полукруга при выбранном отображении. Для этого достаточно взять еще по одной точке на каждой из частей границы полукруга, например, (точка
на рис. 2.42,а) и
(точка
на рис. 2.42,а), найти их образы и по направлению обхода границы определить вид области.
Так, в случае точке
соответствует
, точке
соответствует
. Образом полукруга будет третий квадрант (рис. 2.42,б).
Если взять , т.е. отображение
, то из соответствия
находим, что образом полукруга будет первый квадрант (рис. 2.42,в)
Третий этап. В случае выбранного выше отображения при
ответом, очевидно, будет
, то есть
. В случае
отображение
приводит к тому же результату. Можно предварительно применить преобразование поворота
, в результате чего получим первый квадрант и окончательный ответ:
, то есть
.
Пример 2.77. Найти образ плоскости с разрезом по лучу при отображении
с условием
.
Решение
Пример 2.78. Отобразить плоскость с разрезом на верхнюю полуплоскость.
Решение
Из свойств отображения и анализа решений примеров 2.74 и 2.77 замечаем, что для отображения плоскости с разрезом по лучу
на верхнюю полуплоскость нужно применить функцию
. В данном случае границa области состоит из двух лучей, пробегаемых дважды и соединяющихся в бесконечности (рис. 2.43). Чтобы получить плоскость с одним разрезом, можно сначала применить преобразование, соединяющее разрезы — сдвиг. При этом одна из точек границы должна отображаться в бесконечно удаленную точку. Следовательно, требуется применить дробно-линейное отображение.
Первый этап. Применим преобразование , где, например,
, то есть
.
Запишем отображение . При этом получим
и
, так как
. Образом данной области будет плоскость c разрезом
(рис. 2.43).
Второй этап. Применяем при условии
. Получим отображение, переводящее заданную область в верхнюю полуплоскость.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание
Глава 3. Конформные отображения
Геометрический смысл аргумента и модуля производной функции комплексного переменного
Пусть дана аналитическая в области $D$ функция $f(z)$. Возьмем точку $z_0in D$, пусть производная функции в этой точке не равна нулю
$$f'(z_0)ne0.$$
Функция $w=f(z)$ отображает область $D$ на плоскости z на множество $E$ в плоскости $w$.
Точке $z_0in D$ соответствует точка $w_0=f(z_0)in E$.
Аргумент $arg f'(z_0)$ есть угол поворота касательной к любой
кривой, проведенной через точку $z_0$ при ее отображении с помощью функции $w=f(z)$ на плоскость $w$.
Модуль $|f'(z_0)|$ можно рассматривать как
величину масштаба в точке $z_0$ при отображении $w$. Если $|f'(z_0 )|>1$, то происходит растяжение бесконечно малого элемента, выходящего из
точки $z_0$. Если $|f'(z_0 )|<1$, то происходит сжатие, при $|f'(z_0 )|=1$ масштаб в окрестности точки $z_0$ не меняется.
Надо заметить, что все сказанное относится к точке и ее малой окрестности. В других точках кривой параметры отображения (коэффициент растяжения и угол поворота) изменяются.
Конформные отображения
Отображение одной плоскости на другую называется
конформным в точке $z$, если все бесконечно малые дуги, выходящие из этой точки, при отображении поворачиваются на один и тот же угол и получают одно и то же растяжение (сжатие).
Иными словами, при конформном отображении сохраняется подобие в бесконечно малых частях. Отображение с помощью аналитической функции является
конформным везде, кроме, быть может, точек, в которых производная данной аналитической функции равна нулю.
Отображение окрестности точки $z_0 $ на окрестность точки
$w_0$, осуществляемое аналитической функцией $w=f(z)$ и обладающее в точке $z_0$ свойством сохранения углов и постоянством растяжений,
называется конформным отображением первого рода, если поворот касательных происходит против часовой стрелки, тогда как в
конформном отображении второго рода касательные поворачиваются по часовой стрелке).
В дальнейшем будем рассматривать только конформные отображения первого рода.
В теории Конформных Отображений различают две основные задачи:
1. При известной функции $f(z)$ найти образ заданной области $D$;
2. Найти функцию $f(z)$, отображающую одну данную область $D$ на
другую данную область $G$.
Конформное отображение $f(z)$ при этом чаще всего рассматривается как взаимно однозначное (однолистное), когда для размещения
образа хватает плоскости $w$. Когда одного листа плоскости $w$ недостаточно, вводим римановы поверхности, которые позволяют строить конформные отображения с помощью многозначных функций.
При осуществлении Конформных Отображений следует использовать следующие общие принципы.
Принцип соответствия границ:
При конформном отображении друг на друга двух областей,
ограниченных замкнутыми жордановыми (без самопересечений) кривыми, между их границами всегда устанавливается взаимно однозначное и взаимно
непрерывное соответствие с сохранением направления обхода границы.
Принцип симметрии:
Пусть область $D$, содержащая в составе своей границы некоторый прямолинейный отрезок $gamma$ (конечной или бесконечной длины), отображается функций $w=f(z)$ на область $E$ так, что $gamma$ переходит в прямолинейный отрезок $Gamma$, входящий в границу области. Тогда область $D^{*}$, симметричная области $D$, относительно $gamma$, с помощью аналитической функции $w=f(z)$ отображается в область $E^{*}$, симметричную $E$, относительно $Gamma$.
Линейная функция
Отображение, осуществляемое линейной функцией $$ w = az + b,$$ где $a$ и $b$ — постоянные комплексные числа ($aneq0$), является конформным в расширенной комплексной плоскости.
Геометрический смысл.
Отображение, осуществляемое линейной функцией, складывается из
-
преобразования подобия (растяжение или сжатие с коэффициентом $r=|a|$) относительно начала координат,
-
поворота на угол $alpha=mbox{arg } a$ вокруг начала координат,
-
сдвига на вектор $b$.
Линейное отображение преобразует прямые в прямые (углы между прямыми сохраняются) и окружности в окружности. Покажем это свойство для окружностей.
$$
|z-z_0|=R, quad w=az+b ,,Rightarrow
$$
$$
z=displaystylefrac{w-b}{a}, quad |z-z_0|=displaystylefrac{|w-b-az_0|}{|a|}=R ,,Rightarrow
$$
$$
|w-b-az_0|=R|a| mbox{ — окружность с центром в точке } w_0=b+az_0.
$$
Замечание.
1. Линейное отображение будет однозначно определено, если известны $z_1neq z_2$, переходящие в $w_1neq w_2$:
$$
displaystylefrac{z-z_1}{z_2-z_1}=displaystylefrac{w-w_1}{w_2-w_1}.
$$
2. Линейное отображение будет однозначно определено, если известны $z_1rightarrow w_1$, $k=w’$:
$$
w-w_1=k(z-z_1).
$$
Инверсия
Инверсия $$ w=frac{1}{z}$$ является конформным отображением в расширенной комплексной плоскости.
Точка $z=0$ конформно отображается в $w=infty$, точка $z=infty$ конформно отображается в $w=0$. Доказательство конформности дано далее для более общего случая с дробно-линейной функцией.
Геометрический смысл.
Отображение, осуществляемое инверсией, складывается из двух симметричных отображений
-
относительно единичной окружности,
-
относительно действительной оси.
Круговое свойство.
Инверсия преобразует в окружность всякую окружность (прямые линии условно считаются окружностями с бесконечно большим радиусом).
Докажем это свойство.
Для окружности с центром в точке $z=0$ доказательство очевидно (например, через показательную форму комплексного числа):
$$
|z|=R ,, rightarrow ,, |w|=displaystylefrac{1}{R}.
$$
Рассмотрим произвольную окружность (включая, прямую):
$$
A(x^2+y^2)+Bx+Cy+D=0.
$$
$$
w=displaystylefrac{1}{z} ,, z=displaystylefrac{1}{w},
$$
$$
z=displaystylefrac{1}{u+mathbf iv}=displaystylefrac{u-mathbf i v}{u^2+v^2}.
$$
Подставим
$$
x=displaystylefrac{u}{u^2+v^2}, ,, y=-displaystylefrac{v}{u^2+v^2}
$$
в уравнение окружности и получим уравнение окружности (включая прямую) на плоскости $w$.
$$
D(u^2+v^2)+Bu-Cv+A=0
$$
Нетрудно заметить, что если линия (окружность или прямая) на плоскости $z$ проходит через точку $z=0$, то на плоскости $w$ ее образом является прямая. В противном случае — окружность.
Дробно-линейное отображение
Дробно-линейная функция
$$
w=frac{az+b}{cz+d},
$$
где $a$, $b$, $c$, $d$ – постоянные комплексные числа ($cneq0$, $ad-bcneq0$), является конформным в расширенной комплексной плоскости.
Считаем, что $cneq0$ (иначе получим линейную функцию) и $ad-bcneq0$ (иначе получим функцию тождественно равную константе).
Покажем, что отображение конформно во всех точках расширенной комплексной плоскости, включая $z=-frac{d}{c}$ и $z=infty$.
Круговое свойство:
i
Дробно-линейная функция отображает всякую окружность (включая прямую) в окружность.
Докажем это, записав $w$ как суперпозицию трех отображений (линейного, инверсии, линейного) для каждого из которых круговое свойство доказано:
$$
w=frac{az+b}{cz+d}= frac{caz+cb+ad-ad}{c(cz+d)}=
$$
$$
=frac{a(cz+d)}{c(cz+d)}+ frac{bc-ad}{c(cz+d)}=
$$
$$
=frac{a}{c}+frac{bc-ad}{c}frac{1}{cz+d}.
$$
Замечание 1.
При решении прямой задачи (нахождение образа области при известном отображении) удобно пользоваться принципом сохранения границ, определяя сначала образ границы области на плоскости $w$.
Замечание 2.
Если граница $Gamma$ области $D$ проходит через точку $z=-displaystylefrac{d}{c}$, то ее образом при дробно-линейном отображении $w=displaystylefrac{az+b}{cz+d}$ является прямая. Если не проходит — образом будет окружность.
Замечание 3.
Если образ границы $Gamma$ области $D$ — прямая, то ее уравнение можно найти по двум точкам.
Замечание.
Дробно-линейное отображение будет однозначно определено, если известны $z_1neq z_2neq z_3$, переходящие в $w_1neq w_2neq w_3$:
$$
displaystylefrac{z-z_1}{z-z_2}cdotdisplaystylefrac{z_3-z_2}{z_3-z_1}=displaystylefrac{w-w_1}{w-w_2}cdotdisplaystylefrac{w_3-w_2}{w_3-w_1}.
$$
Принцип симметрии
При решении обратной задачи (нахождение отображения по известной области $D$ на плоскости $z$ и ее образу $E$ на плоскости $w$) удобно пользоваться принципом симметрии:
i
Произвольное дробно-линейное отображение преобразует любые точки $z$ и $z^{*}$, симметричные относительно окружности $Gamma$ (в том числе и прямой) на плоскости $z$, в точки $w$ и $w^{*}$, симметричные относительно образа $w(Gamma)$ этой окружности на плоскости $w$.
Точки $z$ и $z^{*}$ называются симметричными относительно прямой, если они лежат по разные стороны от этой прямой на одинаковом от нее расстоянии, а соединяющий их отрезок перпендикулярен этой прямой.
Точки $z$ и $z^{*}$ называются симметричными относительно окружности $Gamma$ в $mathbb C_{}$, если они лежат на одном луче, выходящим из центра $z_0$ окружности $Gamma$, и произведение их расстояний до центра окружности равно квадрату радиуса $R$ этой окружности, то есть $$mbox{arg}, (z^{*}-z_0)=mbox{arg}, (z-z_0),$$
$$|z^{*}-z_0|cdot|z-z_0|=R^2.$$
При приближении точки $z$ к центру окружности $Gamma$ симметричная ей точка $z^{*}$ стремится к бесконечно удаленной точке. Тогда центр $z_0$ окружности $Gamma$ и бесконечно удаленную точку $z=infty$ будем считать симметричным относительно окружности $Gamma$.
Введенное определение симметрии относительно окружности можно рассматривать как развитие понятия симметрии относительно прямой.
Основные задачи нахождения ДЛО
-
Найти общий вид функции $w$: $$ z_1rightarrow0, ,, z_2rightarrowinfty.$$
-
Найти общий вид функции $w$: $$ mathfrak{I}mathbf{m}(z)>0rightarrow |w|<1, ,, z_0 (mathfrak{I}mathbf{m}(z_0)>0) rightarrow w_0=0. $$
-
Найти общий вид функции $w$: $$ |z|<1 rightarrow |w|<1, ,, z_1 (|z_1|<1) rightarrow w_1=0. $$
Целая степенная функция
$$ w=z^n, quad nin mathbb Z_{}, quad n>1. $$
Функция $w=z^n$ отображает расширенную комплексную плоскость $z$ на расширенную комплексную плоскость $w$.
Не является конформным при $z=0$, так как $$w’=n,z^{n-1} =0 ,, mbox{при } z=0.$$
Не является однолистной, так как всякая точка $w$, отличная от $w=0$ и $w=infty$, имеет $n$ различных прообразов. Для однолистности отображения следует брать на плоскости $z$ лишь сектор вида
$$kcdotdisplaystylefrac{2pi}{n}leqslant mbox{arg},zleqslant(k+1)cdotdisplaystylefrac{2pi}{n},,, kin mathbb Z_{}.$$
Исследуем поведение функции около точки $z=0$.
При помощи степенной функции $$ w=z^n $$ угол с вершиной в начале координат плоскости $z$ отображается в угол с вершиной в начале координат плоскости $w$ c раствором в $n$ раз большим:
$$
z=rho e^{mathbf i varphi},, rightarrow ,, w = z^n=rho^n e^{mathbf i nvarphi}.
$$
Отображение будет взаимно однозначным, если раствор угла на плоскости $w$ будет не более $2pi$.
П
Найти в какую область преобразуется квадрат
$$ 0le xle 1,quad 0le yle 1 $$ функцией $w=z^2+z-1$.
Решение. Выделим вещественную и мнимую части: $$
begin{array}{l}
u=x^2-y^2+x-1, v=2xy+y.
end{array}
$$
Определим образы участков границ данного квадрата:
begin{equation}
OA:quadleft{begin{array}{l} y=0, 0le xle1
end{array}right.quadhbox{дает}quad
left{begin{array}{l}
u=x^2+x-1, v=0.
end{array}right.
end{equation}
это отрезок вещественной оси $-1le ule 1$.
begin{equation}
AB:quadleft{begin{array}{l} x=1, 0le yle1
end{array}right.quadhbox{дает}quad
left{begin{array}{l}
u=1-dfrac{v^2}9, 0le vle3
end{array}right.hskip17.5pt
end{equation}
это часть параболы в первом квадранте.
Образы отрезков $BC$ и $CO$ также являются дугами парабол:
begin{equation}label{eq g3 p5 3}
BC:quad u=frac14big(v^2-9big),quad 1le vle 3,
end{equation}
begin{equation}label{eq g3 p5 4}
CO:quad u=-1-v^2,quad 0le vle1.
end{equation}
Так как точка $z=displaystylefrac12(1+i)$ переходит в точку $w=i-displaystylefrac12$, то внутренность квадрата переходит во внутренность криволинейного
четырехугольника.
Ответ: Внутренность квадрата переходит во внутренность криволинейного четырехугольника.

Радикал
Рассмотрим функцию
begin{equation}
w=sqrt[n]{z},
end{equation}
обратную степенной функции $z=w^n$.
Примем, что $$w=infty mbox{ при } z=infty.$$
Во всех точках расширенной плоскости $z$, кроме точек
$z=0$ и $z=infty$ (где эта функция соответственно равна $w=0$ и $w=infty)$, эта функция $n$-значна и все ее $n$ различных значений для каждого
фиксированного $z=re^{ivarphi}$ (не равные 0 и $infty$) дает формула:
$$ w=sqrt[n]{r}cdot e^{itfrac{scriptstylearg z+2pi k}
{scriptstyle n}} =sqrt[n]{r}cdot e^{itfrac{scriptstylearg z} {scriptstyle n}}cdot e^{itfrac{scriptstyle2pi k}{scriptstyle
n}}quadhbox{при}
quad k=0,1,dots,n-1.
$$
Через $w_k$ обозначим множество всех точек $w$, соответствующих данному фиксированному значению $k$. В результате получим $n$ функций
$w_k$, $k=0,2,dots,n-1$, называемых ветвями многозначной функции $w=sqrt[n]{z}$.
$$ w_k= sqrt[n]{r}cdot e^{itfrac{scriptstylearg z} {scriptstyle n}}cdot e^{itfrac{scriptstyle2pi k}{scriptstyle
n}}quadhbox{при}
quad k=0,1,dots,n-1.
$$
Очевидно, $$ w_{k+1}=w_k cdot
e^{itfrac{scriptstyle 2pi k}{scriptstyle n}}.
$$
Рассмотрим какую-нибудь ветвь $w_k$ функции
и заставим точку $z$ описать в плоскости какую-нибудь замкнутую
кривую.

Если эта кривая не содержит внутри себя точку $z=0$ (сплошная кривая на рисунке), то непрерывно
изменяющийся аргумент точки $z$ вернется к прежнему значению с возвращением точки $z$ в исходное положение. В силу этого и ветвь $w_k$ радикала
останется прежней (т.е. мы вернемся к прежнему значению корня в исходной точке).
Картина изменится, если кривая $l$ будет содержать внутри себя
точку $z=0$ (пунктирная кривая на рисунке). В этом случае после полного обхода кривой $l$ аргумент точки $z$ в исходном положении
увеличится на $pm 2pi k$ (в зависимости от того, совершается ли обход кривой против или по часовой стрелки), в силу чего мы от значения $w_k$
корня в исходной точке перейдем либо к значению
$$ w_kcdot e^{itfrac{scriptstyle2pi}{scriptstyle n}}=w_{k+1},$$
либо к значению
$$ w_kcdot e^{-itfrac{scriptstyle2pi}{scriptstyle n}}=w_{k-1}. $$
Повторяя обход вокруг начала координат в
том или ином направлении достаточное количество раз, мы можем перейти от исходной ветви $w_k$ радикала к любой другой ветви. Очевидно, что после
$n$ обходов начала координат в одном направлении мы возвращаемся к исходной ветви радикала.
Точка, обладающая тем свойством, что обход вокруг нее переводит от одной ветви многозначной функции к другой ветви, называется точкой
разветвления этой функции. Таким образом, точка $z=0$ будет точкой разветвления функции $w=sqrt[n]{z}$.
Из сказанного следует, что мы можем выделить $n$ однозначных ветвей $w_k$ функции $w=sqrt[n]{z}$ только в такой области $D$, которая не
содержит ни одной замкнутой кривой, заключающей внутри себя точку $z=0$.

Расширенная плоскость $z$ с любым разрезом от точки $z=0$ до точки $z=infty$ и, в частности, с разрезом вдоль положительной части вещественной
оси (левая часть рисунка) не содержит ни одной замкнутой кривой, обходящей точку $z=0$. На ней можно выделить $n$ однозначных ветвей
$w_k$, $k=0,1,dots,n-1$, радикала, принимающих каждая одно из значений $sqrt[n]{z}$.
Эти ветви будут однолистно отображать расширенную плоскость $z$ с разрезом вдоль положительной части вещественной оси на секторы $$
kfrac{2pi}n<arg wle(k+1)frac{2pi}n,quad k=0,1,dots,n-1, $$ расширенной плоскости $w$ (правая часть рисунка, где $n=6$). Отображения обратны рассмотренному ранее отображению $w=z^n$ и непрерывны. Для того чтобы фиксировать какую-либо из ветвей $w_k$ радикала,
достаточно лишь указать, в каком из секторов должно изменяться $w$.
Показательная функция
Рассмотрим показательную функцию $$ w=e^z,quad z=x+iy. $$
Перепишем $$ w=e^x(cos y+isin y)=r(cosvarphi+isinvarphi), $$
поэтому
$$
r=|w|=e^x,quadvarphi=mbox{arg},w=y. $$
Линии $x=hbox{const}$ переходят в окружности $r=hbox{const}$ ($y$ и $varphi$ — любые),
Линии $y=mbox{const}$ переходят в лучи $varphi=mbox{const}$ ($x$ и $r$ — любые).
Для взаимной однозначности при отображении с помощью функции $w=e^z$ необходимо и
достаточно, чтобы отображаемая область не содержала никакой пары различных точек $z_1$ и $z_2$, для которых $z_1-z_2=2pi ki$, $kin N$. Этому
условию удовлетворяет любая горизонтальная полоса шириной меньше $2pi$, например, полосы $2pi k<mathfrak{Im}, z<2pi(k+1)$.
-
Полоса $0<mathfrak{Im}, z<pi$ плоскости $z$ отображается функцией $w=e^z$ на верхнюю полуплоскость плоскости $w$
-
Полоса $0<mathfrak{Im}, z<2pi$ — на плоскость $w$ с разрезом по положительной части вещественной оси, при этом прямые $y=0$ и $y=2pi$ отображаются в лучи $varphi=0$ и $varphi=2pi$, т.е. обе в положительную вещественную ось (поэтому нужен разрез).
-
Полуполоса $-infty<mathfrak{Re}, z<0$, $0<mathfrak{Im} z<pi$ отображается в единичный полукруг $|w|<1$, $mathfrak{Im} w>0$.
-
Полуполоса $0<mathfrak{Re}, z<infty$, $0<mathfrak{Im},z<pi$ — на полуплоскость $mathfrak{Im}, w>0$, из которой удален единичный полукруг.
Логарифмическая функция
Логарифмическая функция обратна показательной, бесконечнозначна, все ее значения вычисляются по формуле
$$ w=mbox{Ln }z=mbox{ln }|z|+imbox{Arg }z=mbox{ln }|z|+i(mbox{arg }z+2pi k),quad k=0,pm1,pm2,dots . $$
Дополнительно примем, что $w=infty$ при $z=0$ и $z=infty$.
Обозначив через $w_k$ множество всех
точек $w$, соответствующих данному фиксированному значению $k$, получим бесконечное множество функций, которые называются ветвями многозначной функции $w=mbox{Ln }z$
$$ w_k= mbox{ln }|z|+imbox{Arg }z=mbox{ln }|z|+i(mbox{arg }z+2pi k),quad k=0,pm1,pm2,dots . $$
Бесконечнозначность логарифма связана с бесконечнозначностью его мнимой части $mbox{Arg }z$. Поэтому область не должна допускать обхода начала координат по непрерывной кривой, так как при таком обходе значение $mbox{Arg }z$ изменяется на $2pi$. Область
указанного типа будет сектором концентрического кольца: $$ 0<r_1le rle r_2,quad -pileftarrowvarphi_1levarphilevarphi_2<pi. $$
Каждая ветвь $w_k$ является однозначной функцией. Например, его главное значение $$
mbox{ln }z=mbox{ln }|z|+imbox{arg }z.
$$
Функция $mbox{Ln }z$ отображает всю плоскость с разрезом на горизонтальную полосу однозначно. Если аргумент $z$ увеличить на $2pi$, будет другая ветвь, которая отображает всю плоскость с разрезом (другой лист римановой поверхности) на другую полосу.
$z=0$ — точка разветвления.
Вещественная и мнимая части этой функции
$$
u=displaystylefrac12mbox{ln }(x^2+y^2), ,, v=mbox{arctg }frac{y}{x}+2pi k.
$$
имеют непрерывные частные производные, удовлетворяющие условиям Коши-Римана.
А это значит, что выделенная ветвь логарифма представляет собой дифференцируемую функцию комплексного переменного $z$ в области $D$. Производная ее не обращается в нуль и, следовательно, функция $w=mbox{ln }z$ осуществляет конформное отображение области $D$ на некоторую область плоскости $w$.
П
Найти образ плоскости с разрезом вдоль
положительной части вещественной оси при отображении однозначной ветвью логарифма, когда $z_0=i$ переходит в $w_0=displaystylefrac52pi i$.
Решение. В области $D$, представляющей собой плоскость $z$ с разрезом вдоль положительной части вещественной оси, $$
z=|z|(cosvarphi+isinvarphi),quad |z|>0, 0<varphi<2pi, $$ выделим ветвь логарифма $$ w=ln|z|+ivarphi. $$ Эта ветвь отображает $D$ на
полосу $0<v<2pi$ (здесь принимаем $w=u+iv$). Далее имеем $$ w(i)=displaystylefrac12pi i. $$ Чтобы получить $w_0 =displaystylefrac52pi i$, надо взять $w(i)+2pi
i=displaystylefrac52pi i$. А ветвь $$ w=ln|z|+i(varphi+2pi) $$ отображает $D$ на полосу $2pi!<!v!<!4pi$, содержащую точку $w_0=displaystylefrac52pi i$.
Ответ: $2pi<v<4pi$.
Функция Жуковского
Так называют функцию
begin{equation}label{eq g3 p9 1}
w=frac12left(z+frac1{z}right).
end{equation}
Ее производная $$ w’=frac12left(1-frac1{z^2}right) $$ конечна и отлична от нуля во всех точках плоскости $z$, кроме точек $z=0,+1,-1$, в
силу чего отображение конформно в плоскости $z$, исключая три упомянутые точки.
Установим условие однолистности отображения. Пусть $z_1!ne!z_2$, но $w_1=w_2$, т.е. $$
frac12left(z_1+frac1{z_1}right)=
frac12left(z_2+frac1{z_2}right).
$$ Переписав последнее равенство в виде $$
big(z_1-z_2big)left(1-frac1{z_1z_2}right)=0
$$ найдем из него, что
$$z_1z_2 =1.$$
Следовательно, отображение будет однолистным в любой области, не содержащей никаких двух точек, связанных
равенством $z_1z_2 =1$.
Этому условию удовлетворяют, в частности, круг $|z|<1$ и внешность круга $|z|>1$.
Для того чтобы лучше представить себе рассматриваемое отображение, положим $$ z=re^{ivarphi},quad w=u+iv $$ и произведя соответствующие замены
в функции Жуковског и отделив вещественные и мнимые части, получим два вещественных равенства, зависящие от двух параметров
$$ u=frac12left(r+frac1rright)cosvarphi,quad v=frac12left(r-frac1rright)sinvarphi. $$
Рассмотрим две упомянутые выше области $|z|<1$ и $|z|>1$.
В области $|z|<1$ возьмем окружность
$$|z|=r<1.$$
Из параметрической записи исключим
угол $varphi$. Получим, что эта окружность при отображении перейдет в эллипс $$
frac{u^2}{a^2}+frac{v^2}{b^2}=1
$$ с полуосями $$ a=frac12left(r+frac1rright),quad b=frac12left|r-frac1rright| $$ и полуфокусным расстоянием $$ c=sqrt{a^2-b^2}=1, $$
не зависящим от радиуса $r$ окружности $|z|=r$. Таким образом, окружности $|z|=r$, $0<r<1$, при данном отображении перейдут в софокусные эллипсы
с полуосями $a$ и $b$, фокусы которых находятся в точках $(pm1,0)$.
Так как $r-dfrac1r<0$ при $r<1$, то из представления вещественной и мнимой частей следует, что при положительном направлении обхода окружностей
$|z|=r$ соответствующие эллипсы обходятся в отрицательном направлении. При $rto0$ будет $atoinfty$ и $btoinfty$. Следовательно, при $rto0$
эллипсы, постепенно округляясь, увеличиваются и заполняют всю плоскость $w$. При $rto1-0$ будет $ato1$ и $bto0$, и эллипсы постепенно
вырождаются в разрез вдоль интервала $[-1,1]$ вещественной оси плоскости $w$.
Рассмотрим, во что преобразуются лучи, выходящие из начала координат.
Для этого исключим $r$ из уравнений для вещественной и мнимой частей. Получим $$
frac{u^2}{cos^2varphi}-frac{v^2}{sin^2varphi}=1
$$ уравнение гиперболы с полуфокусным расстоянием $$ c=sqrt{a^2+b^2}=1. $$ Следовательно, отображение переводит лучи $arg z=varphi$ в
семейство гипербол с теми же фокусами $(pm1,0)$, что и у семейства эллипсов (вершины гипербол выколоты).
Итак, функция Жуковского однолистно и конформно отображает круг $|z|<1$ на всю плоскость $w$ с разрезом вдоль вещественной оси от точки
$w=-1$ до точки $w=1$. При этом верхняя полуокружность переходит в нижний берег разреза, а нижняя полуокружность — в верхний берег разреза.

Верхний единичный полукруг $|z|<1$, $mathfrak{Im} z>0$ функция Жуковского отобразит на нижнюю полуплоскость $mathfrak{Im} w<0$, а нижний
полукруг $|z|<1$, $mathfrak{Im} z<0$ — на верхнюю полуплоскость $mathfrak{Im} w>0$.
Рассмотрим теперь в области $|z|>1$ окружности $|z|=r$, где $1<r<+infty$.
Проведя точно такой же анализ, как и в предыдущем случае, легко
доказать, что функция Жуковского отображает эти окружности на те же самые эллипсы, что и в предыдущем случае, но проходимые в
положительном направлении.
При $rto1+0$ эти эллипсы вырождаются в разрез $[-1,1]$ вещественной оси $u$, а при $rto+infty$ эллипсы,
округляясь, увеличиваются и заполняют всю плоскость $w$.
Таким образом, функция $w=frac12left(z+frac1{z}right)$ однолистно и конформно отображает
область $|z|>1$ на всю плоскость $w$ с разрезом вдоль вещественной оси от точки $w=-1$ до точки $w=1$. При этом верхний полукруг отображается на
верхнюю полуплоскость, а нижний полукруг — на нижнюю полуплоскость.
Обратная к функции Жуковского функция $$ w=z+sqrt{z^2+1} $$ двузначна, что обусловлено двузначностью квадратного корня. Каждую точку $z$ она
отображает в две точки $w_1$ и $w_2$, связанные условием $w_1w_2=1$. Легко показать, что точки $z=-1$ и $z=1$ будут точками разветвления этой
функции. Таким образом, в любой области, не содержащей замкнутых кривых, обходящих лишь одну из этих точек, можно выделить две однозначные ветви
обратной функции. Этому условию, в частности, удовлетворяет вся плоскость $z$ с разрезом вдоль отрезка $[-1,1]$ вещественной оси. Ветви обратной
функции однолистно отображают плоскость $z$ с указанным разрезом либо на круг $|w|<1$, либо на круг $|w|>1$ и аналитичны.
Тригонометрические функции
Теорема Римана. Основные принципы конформных отображений
Теорема 1 (Римана).
Всякую односвязную область $D$
комплексной плоскости $z$, граница которой состоит более чем из одной точки, можно конформно отобразить на внутренность единичного круга $|w|<1$
плоскости $w$ и притом бесконечно многими способами.
Теорема 2 (Римана).
Функция $w=f(z)$, осуществляющая
конформное отображение заданной односвязной области $D$ $($граница которой состоит более чем из одной точки$)$ на единичный круг $|w|<1$
определена единственным образом, если выполняются условия: $$ w_0=f(z_0)quadhbox{и}quadarg f'(z_0)=alpha, $$ где $z_0in D$, $w_0$ —
центр круга, $alpha$ — заданное вещественное число.
Применения конформных отображений
Конформные отображения имеют многочисленные применения.
Например, они применяются в картографии при построении географических карт [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Каждая географическая карта изображает часть земной поверхности на плоскости (на листе бумаги). При таком изображении очертания материков и морей подвергаются искажению. Оказывается, однако, что можно строить карту, не изменяя величины углов между различными линиями на земной поверхности, с помощью стереографической проекции и конформных отображений.
Наиболее важные применения конформных отображений относятся к вопросам физики и механики [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Например, задачи, где требуется вычислить электрический потенциал в точках пространства, окружающего заряженный конденсатор, или вычислить температуру внутри нагретого тела, вычислить скорости частиц жидкости или газа в потоке, движущемся в некотором канале и обтекающем при этом какие-либо препятствия и т.п, решаются без больших трудностей случае, когда тела имеют простую форму. Конформные отображения простой фигуры посредством некоторой функции комплексного переменного позволяют перейти к фигуре с более сложной формой, когда задача в простейшем случае уже решена.
Известный пример — расчет профиля крыла самолета [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Задача о скоростях частиц потока воздуха, обтекающего крыло самолета, сводится к более простой задаче обтекания круглого цилиндра с помощью функции Жуковского (Николай Егорович Жуковский (1847-1921) широко использовал комплексные числа и конформные отображения для расчета самолетов). На рисунке показан профиль крыла самолета в поперечном сечении (рис. снизу) и более простая форма — круг, то есть само тело — круглый цилиндр (рис. сверху)

-
Существование
обратной функции для аналитической
функции в окрестности точки
Пусть
f(z)
= u(x,y)
+iv(x,y)
аналитична в точке z0
и f(z0)0
w=f(z):
.
Якобиан
в окрестности точки z0.
Следовательно,
имеет
смысл коэффициента искажения площади
в точке
при
отображении
и
существует
обратная функция в некоторой окрестности
точки
, причём
.
-
Геометрический
смысл аргумента производной.
Пусть
-гладкая кривая Жордана,
.Обозначим
образ кривой
при отображении f.
Предположим, что f(z)
аналитическая в точке z0
функция и
.
Имеем
.
Так как при умножении комплексных чисел
аргументы складываются, то
Если
— главные
значения аргументов,
— угол поворота кривой в точке z0
при отображении w
= f(z),
определяемый с точностью до
.
Как видим, этот угол не зависит от выбора
кривой, проходящей через данную точку.
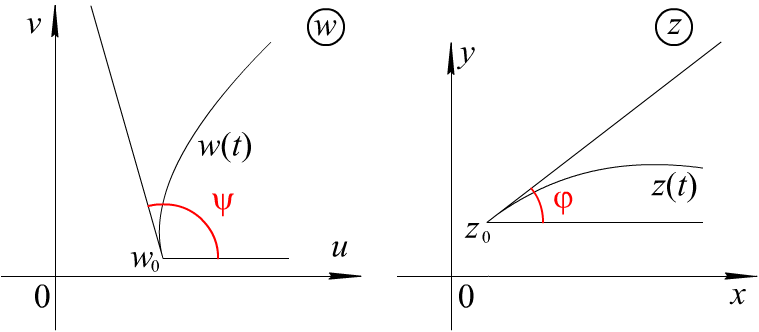
Рис.
2.2.
В
частности, если в плоскости z
пересекаются
две кривые
,
имеющие в точке пересечения главные
значения аргументов
,
а их образы при отображении w=f(z),
соответственно, углы
,
то мы получим
,
откуда,
вычитая одно равенство из другого,
получим
.
Полученное
равенство позволяет сформулировать
следующее
Следствие.
При сделанных предположениях (аналитичность
в точке и неравенство нулю производной
) углы при отображении сохраняются.
Кроме того, сохраняется «порядок обхода».
Например, если поворот от касательной
к первой кривой в точке пересечения к
касательной второй кривой в плоскости
z
происходит против часовой стрелки, то
тоже самое будет наблюдаться и в плоскости
w
между образами этих кривых.
Пример:
.
Обратить внимание на сохранение углов
и направлений поворота (9 точек пересечений)
pic2_3
-
Геометрический
смысл модуля производной.

Таким
образом,
—коэффициент
линейного растяжения кривой в точке
при заданном отображении.
Коэффициент
растяжения кривой в точке, не зависит
от кривой, проходящей через эту точку.
Это коэффициент равен |f(z0)|.
Это свойство называется свойством
сохранения масштаба в точке z0.
Как уже отмечалось,
является коэффициентом растяжения
площади в точке z0
при этом отображении.
Пример:
Обратить внимание на изменение площади
при отображении
в окрестности точки
.
Линейные размеры увеличиваются
приблизительно в 2 раза (
).
Площадь в 4 раза.
pic2_4
-
Конформные
отображения.
Определение
(Конформность в C).
Непрерывное, взаимнооднозначное
отображение w=f(z)
области D
на область D*
называется конформным, если в каждой
точке D
имеет место
-
свойство
сохранения углов -
сохранение
масштабов
в перечисленном
выше смысле.
Как мы
видели, если f(z)
аналитична в точке z0
и f(z0),
то отображение w=f(z)
конформно в некоторой окрестности точки
z0.
Определение.
Если две кривые
пересекаются
в бесконечности, например, при
,
то
углом между кривыми
в
бесконечности называется угол в
0
между
образами этих кривых при отображении
,
то
есть между кривыми
в
точке
.
Аналогично,
определяется понятие «изменение линейных
размеров кривой» в бесконечности.
Именно, если
,
то в
точке
изменение
линейных размеров
определяется
по образу кривой
.
И
в том и в другом случае
предварительно
переводится в
0 отображением
.
С учетом этих определений дается
определение конформности в
.
Определение
(Конформность в расширенной комплексной
плоскости
).
Непрерывное, взаимно однозначное
отображение w=f(z)
области D
на область D*
в
называется
конформным, если в каждой точке D
имеет место
1) свойство
сохранения углов
2) сохранение
масштабов
Если
требуется исследовать вопрос об угле
или коэффициенте растяжения кривой
при
,
то эту задачу можно решить, рассматривая
кривую
в точке
.
При решении задач об изменении углов и
масштабов в
при
отображении
можно
руководствоваться следующей таблицей
|
Решение |
|
|
Задача |
Решение |
|
1. |
См. |
|
2. |
См. в точке w0 |
|
3. |
См. в точке z0 |
|
4. |
См. в точке w0 |
Пример
1. Исследовать на конформность функцию
в
расширенной комплексной области.
Решение.
В точках отличных от i
и
конформность следует из существования
производной и не равенства её нулю
.
В точке
z=i
значение функции w=,
поэтому для исследования в этой точке
нужно рассмотреть функцию
в точке z=i,
(см. таблицу п. 3 ). Конформность следует
из существования производной и не
равенства её нулю при
,
.
В точке
z=
значение
функции w=1,
поэтому для исследования на конформность
в этой точке следует «бесконечность в
аргументе» перевести предварительно
в 0
( с помощью замены переменного
).
Таким образом, для исследования берётся
функция
в точке 0,
которая в этой точке имеет производную,
отличную от нуля,
.
Пример
2. Исследовать на конформность в точке
z=
функцию w=i
z
— 2.
Решение.
Во всех точках z
производная существует и не равна нулю.
При z=
, w=,
поэтому, согласно определению, необходимо
сделать две замены:
,
и
.
В итоге, для исследования на конформность
имеем функцию
в
окрестности точки
.
Эта функция в точке
имеет производную не равную нулю,
.
Пример
3: Докажем непосредственно свойство
сохранения углов в т. 2i
при отображении
.
Пусть
и
выходят из точки 2i.
Для первой кривой
,
для второй
.
Кроме того
Точка 2i
переходит в бесконечность, поэтому
будем искать углы между кривыми
и
в
точках
,
соответственно. Для этих кривых имеем
,
поэтому угол между образами wk
в бесконечности будет равен:

Некоторые свойства
конформных отображений ( без доказательства
)
Свойство
сохранения области.
Если f(z)
аналитична и однолистна (взаимнооднозначна)
в области D,
то f(z)0
в D
и f(z)
конформно отображает D
на D*
. Кроме того, f
-1(w)
аналитична в D*,
где D*
образ D
при отображении f(z).
Свойство
сохранения границ.
Пусть D
и D*
две области, ограниченные замкнутыми
кривыми Жордана
и
.
Если f(z)
отображает D
на D*
конформно, то она отображает
на
взаимнооднозначно и взаимно непрерывно
с сохранением направления обхода
границы.
Свойство
взаимнооднозначного соответствия.
Пусть D
и D*
две односвязные области, ограниченные
замкнутыми кусочно-гладкими кривыми
Жордана
и
.
Если аналитическая в D
функция взаимнооднозначно и непрерывно
отображает
на
с
сохранением обхода, то эта функция
конформно отображает D
на D*.
Теорема
( Риман ).
Если граница односвязной области
состоит более, чем из одной точки, то
существует аналитическая функция,
конформно отображающая D
на внутренность круга |z|<1,
причём эта функция единственна, если
задать условия нормировки ( например,
перевести заданную точку z0
с заданным направление в заданную точку
w0
с заданным направлением.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #