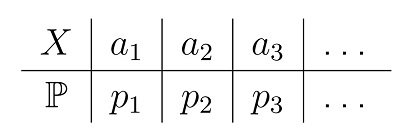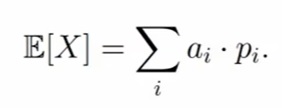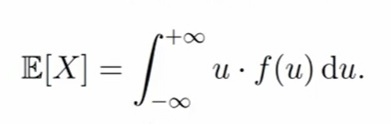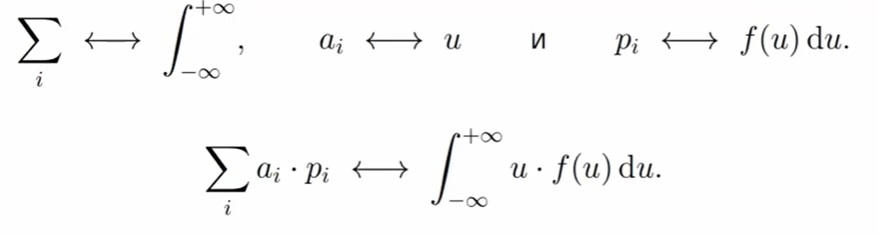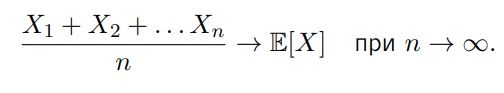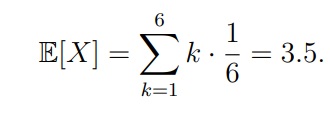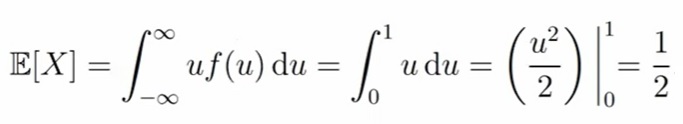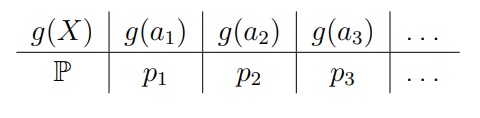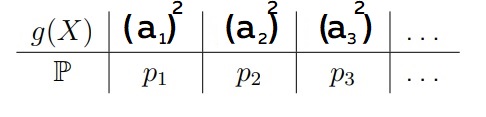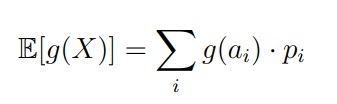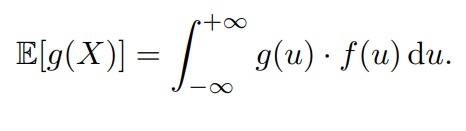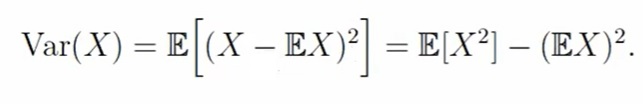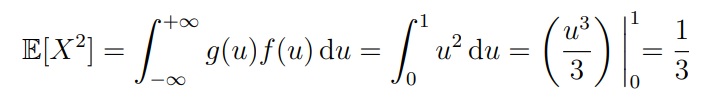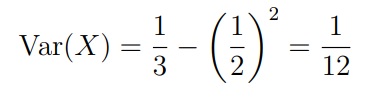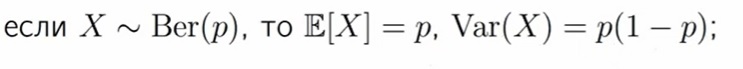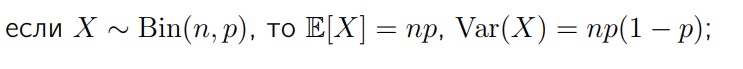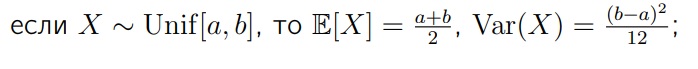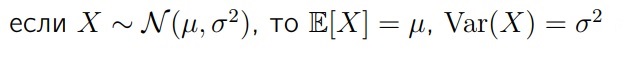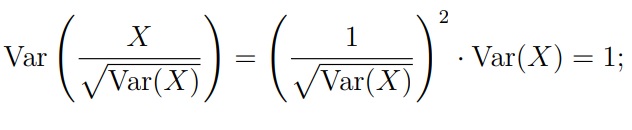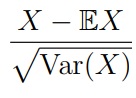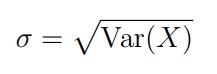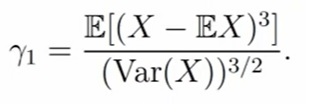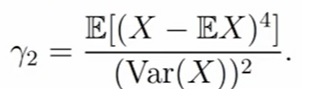Непрерывная случайная величина
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Случайная величина называется непрерывной, если ее функция
распределения
непрерывно дифференцируема. В этом случае
имеет производную, которую обозначим через
– плотность распределения вероятностей.
Плотностью распределения вероятностей непрерывной случайной
величины
называются функцию
– первую производную от функции распределения
:
Из этого определения следует, что функция распределения является
первообразной для плотности распределения.
Заметим, что для описания распределения вероятностей дискретной
случайной величины плотность распределения неприменима.
Вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу
равна определенному интегралу от плотности
распределения, взятому в пределах от
до
.
Зная плотность распределения
,
можно найти функцию распределения
по формуле:
Числовые характеристики непрерывной случайной величины
Математическое ожидание непрерывной случайной величины
,
возможные значения которой принадлежат всей оси
,
определяется равенством:
где
– плотность распределения случайной величины
.
Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения принадлежат интервалу
,
то:
Все свойства математического ожидания, указанные для
дискретных случайных величин, сохраняются и для непрерывных величин.
Дисперсия непрерывной случайной величины
,
возможные значения которой принадлежат всей оси
,
определяется равенством:
или равносильным равенством:
В частности, если все возможные значения
принадлежат интервалу
,
то
или
Все свойства дисперсии, указанные для дискретных случайных
величин, сохраняются и для непрерывных случайных величин.
Среднее квадратическое отклонение
непрерывной случайной величины определяется так же, как и для дискретной
величины:
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Основные законы распределения непрерывных случайных величин
- Нормальный закон распределения СВ
- Показательный закон распределения СВ
- Равномерный закон распределения СВ
Примеры решения задач
Пример 1
Дана
функция распределения F(х) непрерывной случайной величины
Х.
Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания X на отрезок [a,b]. Построить графики функций F(x) и f(x).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
распределения вероятностей:
Математическое
ожидание:
Дисперсию
можно найти по формуле:
Вероятность
попадания на отрезок:
Построим графики функций F(x) и f(x).
График плотности
распределения
График функции
распределения
Пример 2
Случайная величина Х задана плотностью вероятности
Определить константу c, математическое ожидание, дисперсию, функцию распределения величины X, а также вероятность ее попадания в интервал [0;0,25].
Решение
Константу
определим,
используя свойство плотности вероятности:
В нашем случае:
Найдем математическое
ожидание:
Найдем дисперсию:
Искомая дисперсия:
Найдем функцию
распределения:
для
:
для
:
для
:
Искомая функция
распределения:
Вероятность попадания
в интервал
:
Пример 3
Плотность
распределения непрерывной случайной величины
имеет вид:
Найти:
а)
параметр
;
б)
функцию распределения
;
в)
вероятность попадания случайной величины
в интервал
г)
математическое ожидание
и дисперсию
д)
построить графики функций
и
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а)
Постоянный параметр
найдем из
свойства плотности вероятности:
В нашем
случае эта формула имеет вид:
б)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
Остается
найти выражение для
, когда
принадлежит
интервалу
:
Получаем:
в)
Вероятность
попадания случайной величины
в интервал
:
г)
Математическое ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
Среднее
квадратическое отклонение равно квадратному корню из дисперсии:
д) Построим графики
и
:
График плотности вероятности f(x)
График функции распределения F(x)
Задачи контрольных и самостоятельных работ
Задача 1
НСВ на всей
числовой оси oX задана интегральной функцией:
Найти
вероятность, что в результате 2 испытаний случайная величина примет значение,
заключенное в интервале (0;4).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Дана
дифференциальная функция непрерывной СВ Х. Найти: постоянную С, интегральную
функцию F(x).
Задача 3
Случайная
величина Х задана функцией распределения F(x):
а) Найти
плотность вероятности СВ Х — f(x).
б) Построить графики
f(x), F(x).
в) Найти вероятность
попадания НСВ в интервал (0; 3).
Задача 4
Дифференциальная
функция НСВ Х задана на всей числовой оси ОХ:
Найти:
а) постоянный
параметр С=const;
б) функцию
распределения F(x);
в) вероятность
попадания в интервал -4<X<4;
г) построить
графики f(x), F(X).
Задача 5
Случайная величина
Х задана функцией распределения F(x):
а) Найти
плотность вероятности СВ Х — f(x).
б) Построить
графики f(x), F(x).
в) Найти
вероятность попадания НСВ в интервал (0;π⁄2).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 6
НСВ X имеет
плотность вероятности (закон Коши)
а) постоянный
параметр С=const;
б) функцию
распределения F(x);
в) вероятность
попадания в интервал -1<X<1;
г) построить
графики f(x), F(X).
Задача 7
Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:
а) найти
параметр C;
б) при
заданной интегральной функции F(x) найти дифференциальную
функцию f(x), а при заданной дифференциальной функции f(x) найти интегральную
функцию F(x);
в)
построить графики функций F(x) и f(x);
г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(X);
д)
вычислить вероятность попадания в интервал P(a≤x≤b);
е)
определить, квантилем какого порядка является точка xp;
ж)
вычислить квантиль порядка p
Задание 8
Дана
интегральная функция распределения случайной величины X. Найти дифференциальную
функцию распределения, математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение.
Задача 9
Случайная
величина X задана интегральной функцией распределения
Найти
дифференциальную функцию, математическое ожидание и дисперсию X.
Задача 10
СВ Х
задана функцией распределения F(x). Найдите вероятность
того, что в результате испытаний НСВ Х попадет в заданный интервал (0;0,5).
Постройте график функции распределения. Найдите плотность вероятности НСВ Х и
постройте ее график. Найдите числовые
характеристики НСВ Х, если
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Математическое ожидание случайной величины
Закон
распределения
полностью характеризует случайную
величину с вероятностной точки зрения.
Однако при решении многих практических
задач нет необходимости приводить весь
закон распределения случайной
величины,
достаточно указать некоторые величины,
называемые числовыми характеристиками,
назначение которых — это выражение
наиболее существенных особенностей
распределения. Для каждой случайной
величины необходимо знать некоторое
среднее значение, около которого
группируются ее возможные значения,
число, характеризующее степень
разбросанности этих значений относительно
среднего, а также некоторые другие
числовые характеристики.
Одной из
таких характеристик является математическое
ожидание случайной величины.
Определение
6. Математическое
ожидание —
это среднее значение случайной
величины.
Математическое ожидание
случайной величины обозначается
или
.
Если
случайная величина —
дискретная и принимает конечное число
значений, то
(8)
Если случайная
величина —
дискретная и принимает бесконечное, но
счетное число значений, то
(9)
Если случайная
величина —
непрерывная и принимает значения на
конечном промежутке ,
то
(10)
Если
случайная величина —
непрерывная и принимает значения на
всей числовой оси, то
(11)
Встречаются
случайные величины, для которых
математическое ожидание не существует,
так как ряд (9) или
интеграл (11)
расходятся, но такие случайные величины
встречаются редко.
Свойства
математического ожидания.
1. Математическое
ожидание константы равно этой
константе: ;
2. ;
3. ;
4. Определение
7. Две случайные
величины называются независимыми,
если закон распределения одной
из них
не меняется от того, какие возможные
значения приняла другая величина.
Если
случайные величины и
независимы,
то
;
5. =0.
Пример
9. Дан
ряд распределения дискретной случайной
величины :
|
|
2 |
|
4 |
|
|
0,2 |
0,4 |
0,4 |
Известно,
что математическое ожидание .
Найти .
Решение. Так
как дискретная случайная величина
принимает конечное число значений,
воспользуемся
формулой (8), получим
уравнение:
,
из
которого находим :
.
Пример
10. Закон
распределения непрерывной случайной
величины задан
с помощью плотности распределения:
Найти
математическое ожидание данной случайной
величины.
Решение. Так
как непрерывная случайная величина
принимает значения на конечном промежутке,
то для
вычисления математического
ожидания воспользуемся формулой (10),
получаем:
.
Вопрос. Случайная
величина принимает
только отрицательные значения.
Тогда равно:
а)
0;
б) 1;
в) отрицательному числу;
г)
числу из отрезка .



Мода и медиана случайной величины
Определение
8. Модой дискретной
случайной величины называется
ее значение ,
имеющее
наибольшую вероятность.
(13)
Графическим
представлением закона распределения
дискретной случайной величины является
многоугольник
распределения, тогда
мода — это точка, имеющая наибольшую
ординату.
Рис.7
Определение
9. Модой непрерывной
случайной величины называется точка
локального максимума плотности
распределения.
(14)
Рис.8
Мода может
не существовать, может иметь единственное
значение( тогда распределение случайной
величины
называется унимодальным),
может иметь множество значений( в этом
случае распределение называется
мультимодальным).
Определение
10. Медианой случайной
величины называется
такое ее значение ,
относительно
которого равновероятны
получение большего и получение меньшего
значения.
Если —
дискретная случайная величина, то —
это число на отрезке ,
для которого
(15)
Отрезок называется медианным.
Если —
непрерывная случайная величина, то
(16)
то есть медиана
— это корень уравнения:
(17)
Графически
медиана — это абсцисса точки, в которой
площадь под кривой распределения делится
пополам.
Рис.9
Если
распределение унимодальное и симметричное,
то математическое ожидание, мода и
медиана случайной
величины
совпадают.
Пример
11. Дан
ряд распределения дискретной случайной
величины :
|
|
2 |
4 |
6 |
8 |
|
|
0,4 |
0,2 |
0,1 |
0,3 |
Найти
моду и медиану случайной
величины.
Решение. Наибольшую
вероятность имеет значение ,
поэтому .
Так
как ,
а ,
то медианным отрезком является
отрезок ,
тогда
медианой является любое число из этого
отрезка.
Пример
12. Закон
распределения непрерывной случайной
величины задан
плотностью распределения:
Найти моду и
медиану случайной величины.
Решение. Кривой
распределения является парабола, ветви
которой направлены вниз, поэтому она
имеет точку
максимума, найдем
ее, для этого вычислим производную
функции :
.
Точка максимума является корнем
уравнения ,
получаем уравнение
,
из которого находим .
Так
как парабола симметрична относительно
прямой, проходящей через точку ,
параллельно оси ординат,
то распределение
— симметричное, поэтому .
Рис.10
Вопрос. Непрерывная
случайная величина принимает значения
на отрезке ,
распределение симметричное,
.
Тогда .


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Понравилось? Добавьте в закладки
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Понравилось? Добавьте в закладки
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Математикам прошлого не сиделось на месте, дай волю, как они опять что-нибудь придумают и накатают очередной, наскоро состряпанный, фундаментальный манифест. А нам потом разгребать. Сегодня это будет математическое ожидание. Как гласит вики, это одно из важнейших понятий в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины
Математическое ожидание
Для дискретной случайной величины X с таблицей распределения
Математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Для непрерывный случайной величины X с плотностью f(u) математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Математическое ожидание тоже подходит для правила перехода из дискретного случая в непрерывному. Сумму меняем на интеграл, ai меняем на аргумент функции плотности, Pi меняем на f(u)du. Формула следующая:
Как интерпретировать математическое ожидание?
Математическое ожидание это, в некотором смысле, среднее значение случайной величины. Окей, мы перемножили значения на вероятности из таблички. Мы получили какое-то число. Допустим, пять. Что оно значит?
Физический смысл: если на отрезке, распределить единичную массу согласно распределению (в дискретном случае поместив в точки ai массу pi , а в непрерывном — согласно плотности f), то точка E[X] будет координатой «центра масс» отрезка.
Вероятностный смысл: при многократном повторении эксперимента, ассоциированного с X, среднее арифметическое получившихся значений X1, X2, X3, . . . будет стремиться к E[X], т.е. эксперимент мы повторяем бесконечное количество раз и записываем результат (X1, X2, X3…Xn). Если мы посчитаем среднее арифметическое результата n-экспериментов, то это число и будет математическим ожиданием случайной величины, при n стремящемуся к бесконечности
Этот факт называется «Законом больших чисел»
Давайте решим задачку.
Пусть случайная величина X равна числу очков, выпадающих при одном подбрасывании игральной кости. Найти математическое ожидание E[X]
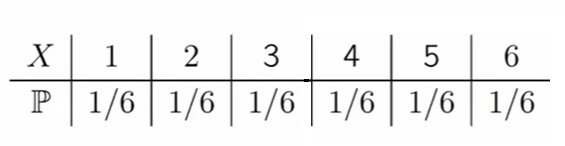
Как мы помним, вероятность выпадения каждой стороны кубика у нас 1/6
Как мы помним по формуле в начале статьи, нам нужна сумма всех возможных значений случайной величины перемноженных на вероятность их наступления (ai x pi):
E[X] = 1*1/6, 2*1/6, 3*1/6, 4*1/6, 5*1/6, 6*1/6 = 21/6 = 3,5
По науке формула будет выглядеть так:
Давайте найдем математическое ожидание (E[X]) равномерного распределения на отрезке от 0 до 1 (Unif[0, 1]). Тут даже без решения понятно, что «центр массы» у нас будет ровно посередине отрезка. С формулой это выглядит так:
Свойства математического ожидания:
- E[c] = c для любого c ∈ R (математическое ожидание для константы будет равно константе)
- E[cX] = cE[X] для любого c ∈ R (константу можно выносить из мат. ожидания)
- E[X + Y ] = E[X] + E[Y] для любых X и Y (мат. ожидание суммы это всегда сумма мат. ожиданий)
- E[X · Y ] = E[X] · E[Y], если X и Y независимы (мат. ожидание произведений — это произведение мат. ожиданий, если случайные величины независимы)
- Если X ≥ 0, то E[X] ≥ 0 (если случайная величина у нас не отрицательна, соотв. мат. ожидание тоже не отрицательно)
Преобразование случайной величины
Очень часто другие характеристики случайных величин тоже вычисляются как математическое ожидание (не обычное, а от некоторого преобразования случайной величины X). Для этого мы будем использовать произвольную функцию g, т.е. в итоге нам нужно будет найти E[g(X)].
В дискретном случае распределение g(X) будет следующим:
Как это будет выглядеть: если у нас математическое ожидание принимает вид E[x2], то случайная величина X примет значение (а1)2 . Заметим, что вероятность (p) остаётся точно такой же
Формула для дискретного распределения:
Формула для непрерывного распределения:
Дисперсия
Если математическое ожидание характеризует среднее значение случайной величины, дисперсия, наоборот, показывает разброс значения случайной величины относительно её математического ожидания. Дисперсия обозначается, как Var(X) и вычисляется по формуле ниже, т.е. дисперсия — это математическое ожидание от формулы случайная величина минус математическое ожидание X в квадрате:
Второй вариант формулы (после второго равно) получается, если применить свойство мат. ожидания. По первому варианту формулы удобней интерпретировать понятие дисперсии. По второму варианту — считать
Стоит заметить, что определение для дискретных и непрерывных распределений — оно одинаковое, однако, мат. ожидание будет считаться в этих случаях по-разному
Как интерпретировать математическое ожидание?
Дисперсия характеризует степень разброса значений случайной величины вокруг её мат. ожидания
Задача
Задача 1. Пусть случайная величина имеет равномерное распределение X ∼ Unif[0, 1]. Найти дисперсию Var(X).
Для решения будем использовать формулу Var(X) = E[X2] − (EX)2
Чтобы найти E[X2], заметим, что это E[g(X)] для g(u) = u2 . Из этого следует, что:
Если E[X] = 1/2, мы получим
Свойства дисперсии
- Var(c) = 0 для любого c ∈ R (дисперсия константы равна нулю)
- Var(cX) = c2 Var(X) для любого c ∈ R (константа тоже выносится с квадратом
- Var(X + Y ) = Var(X) + Var(Y ), если X и Y независимы (дисперсия суммы —
- это сумма дисперсий для независимых случайных величин)
- Var(X + c) = Var(X) для любого c ∈ R (Если мы к случайной величине добавляем константу, то дисперсия никак не учитывает, т.к. это не влияет на сам разброс)
- Var(X) ≥ 0 (дисперсия не может быть отрицательной)
Итого:
Математическое ожидание и дисперсия являются «базовыми» числовыми характеристиками распределений.
Дисперсия для распределение Бернулли: вероятность успеха умноженная на вероятность неуспеха
Дисперсия для биномиального распределения: Все характеристики умножаются на n
Дисперсия для равномерного распределения:
Дисперсия для нормального распределения: Сигма в квадрате
Базовые операции для случайных величин
Центрирование: вычитание из X ее мат. ожидания EX. Это операция позволяет сделать так, чтобы у случайной величины было мат. ожидание, которое равно нулю
E[X − EX] = E[X] − E[X] = 0
Нормирование: деление X на p Var(X). Дисперсию приводим к единице.
Стандартизация: центрирование + нормирование
Среднеквадратическое отклонение (или стандартное отклонение) — это квадратный корень из дисперсии случайной величины:
Разделив случайную величину X на σ, мы получим случайную величину с дисперсией Var(X/σ) = 1. Эта операция называется нормировкой.
Характеристики среднего значения случайной величины
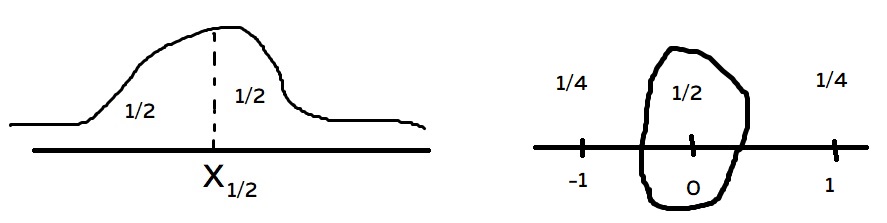
Теоретическая медиана случайной величины X — это число x1/2, удовлетворяющее неравенствам
Медиана — некоторая точка x1/2, которая делит функцию плотности пополам с точки зрения площади под графиком
Теоретическая мода:
• В дискретном случае — значение, которое принимаются с наибольшей вероятностью.
• В непрерывном случае — точка максимума функции плотности
Моменты старших порядков
• E[Xk] — k-ый момент (или момент порядка k)
• E[|X|k] — абсолютный k-ый момент X
• E[(X − EX)k] — центральный k-ый момент X
• E[|X − EX|k] — абсолютный центральный k-ый момент X
Все вышеприведенные моменты характеризуют распределение случайной величины. Они часто появляются в задачах концентрации
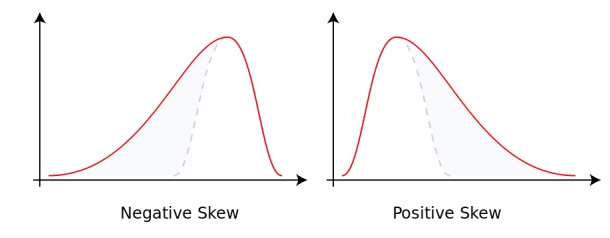
Коэффициент асимметрии (Skewness). Коэффициент асимметрии — величина, характеризующая асимметрию распределения данной случайной величины. Он показывает, если ли у нас скошенность в какую-либо сторону.
Например, вы работаете с выборкой и хотите проверить является ли она «нормальной» — там могут быть ошибки, но если они распределены нормально, то теоретические свойства модели будут хорошими. Чтобы проверить выборку можно использовать коэффициент асимметрии.
Если значение γ1 по модулю большое, то в выборке есть скошенность. Если значение близко к нулю, то ваша выборка нормальная.
γ1 — нормированный центральный момент порядка 3
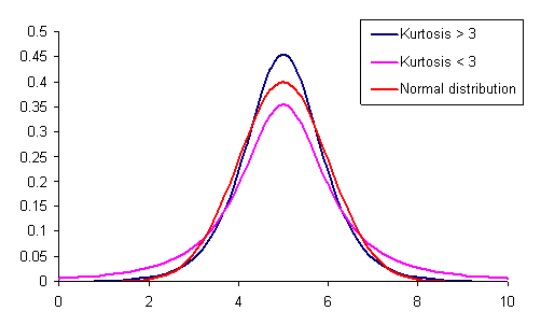
Коэффициент эксцесса (Kurtosis) — величина, которая характеризуют кривизну функции плотности около точки максимума. По научному — это мера остроты пика плотности
распределения случайной величины.
γ2 — нормированный центральный момент порядка 4. Если мы получим коэффициент эксцесса больше трёх, то это означает, что около точки максимума функция плотность имеет более острый пик, если меньше — функция плотности имеет меньшую кривизну
Существуют три правила расчета математического ожидания и они одинаково применимы для дискретных и непрерывных случайных переменных.
Правило 1. Математическое ожидание суммы нескольких переменных равно сумме их математических ожиданий. Например, если имеются три случайные переменные X, Y и Z, то
. (4)
Правило 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если X – случайная переменная и A – константа, то
. (5)
Правило 3. Математическое ожидание константы есть она сама. Например, если A – константа, то
. (6)
Следствие из трех правил:
.
Независимость случайных переменных
Две случайные переменные X и Y называются независимыми, если
(7)
Для любых функций и
. Из независимости следует как важный частный случай, что
.
| < Предыдущая | Следующая > |
|---|