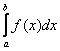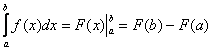Содержание
- Обратное свойство
- Неопределенный интеграл
- Другие значения постоянной интеграции
- Как рассчитывается постоянная интегрирования?
- Примеры
- Пример 1
- Пример 2
- Пример 3
- Предлагаемые упражнения
- Упражнение 1
- Упражнение 2.
- Упражнение 3.
- Упражнение 4.
- Ссылки
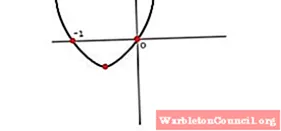
В постоянная интеграции Это дополнительная ценность для вычисления первообразных или интегралов, она служит для представления решений, составляющих примитив функции. Он выражает внутреннюю неоднозначность, когда любая функция имеет бесконечное количество примитивов.
Например, если мы возьмем функцию: f (x) = 2x + 1 и получим ее первообразную:
∫ (2x + 1) dx = х2 + х + C ; куда C это постоянная интеграции и графически представляет вертикальный переход между бесконечными возможностями примитива. Правильно сказать, что (x2 + x) есть а примитивов f (x).
Таким же образом вы можете определить (x2 + х + C ) как примитив f (x).
Обратное свойство
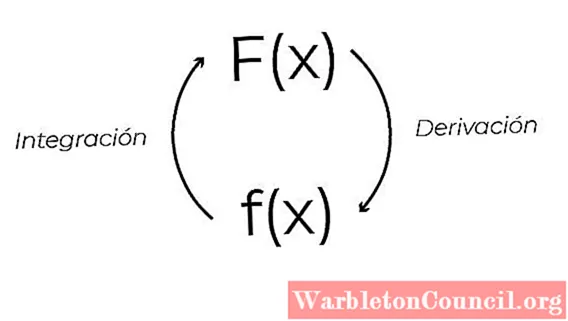
Можно отметить, что при выводе выражения (x2 + x), мы получаем функцию f (x) = 2x + 1. Это связано с обратным свойством, существующим между выводом и интегрированием функций. Это свойство позволяет получать формулы интегрирования, начиная с дифференцирования. Это позволяет проверять интегралы через те же производные.
Однако (x2 + x) — не единственная функция, производная которой равна (2x + 1).
- d (Икс2 + х) / dx = 2x + 1
- d (Икс2 + х + 1) / dx = 2x + 1
- d (Икс2 + х + 2) / dx = 2x + 1
- d (Икс2 + х + 3) / dx = 2x + 1
- d (Икс2 + х + C) / dx = 2x + 1
Где 1, 2, 3 и 4 представляют конкретные примитивы f (x) = 2x + 1. В то время как 5 представляет неопределенный или примитивный интеграл f (x) = 2x + 1.
Примитивы функции получаются посредством первичного или интегрального процесса. Где F будет примитивом f, если верно следующее
- у = ∫ f (x) dx= F (х) + С; C = постоянная интеграции
- F ’(x) = f (x)
Можно видеть, что функция имеет единственную производную, в отличие от ее бесконечных примитивов, полученных в результате интегрирования.
Неопределенный интеграл
∫ f (x) dx = F (x) + C
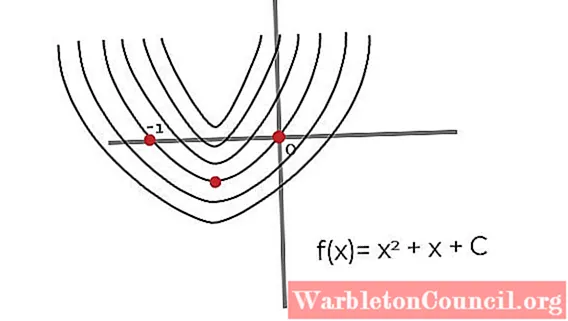
Он соответствует семейству кривых с одинаковым рисунком, которые испытывают несоответствие в значениях изображений каждой точки (x, y). Каждая функция, отвечающая этому шаблону, будет отдельным примитивом, а набор всех функций известен как неопределенный интеграл.
Ценность постоянная интеграции именно он отличает каждую функцию на практике.
В постоянная интеграции предлагает вертикальный сдвиг на всех графиках, которые представляют примитивы функции. Где наблюдается параллелизм между ними, и то, что C это значение смещения.
Согласно общепринятой практике постоянная интеграции он обозначается буквой «C» после добавления, хотя на практике не имеет значения, добавляется или вычитается константа. Его реальную ценность можно найти разными способами в зависимости от первоначальные условия.
Другие значения постоянной интеграции
Уже говорилось о том, как постоянная интеграции применяется в отрасли интегральное исчисление; Представление семейства кривых, определяющих неопределенный интеграл. Но многие другие науки и отрасли приписывают очень интересные и практические ценности постоянная интегрирования, которые способствовали развитию множества исследований.
в физический константа интегрирования может принимать несколько значений в зависимости от характера данных. Очень распространенный пример — знание функции V (т) который представляет собой скорость частицы в зависимости от времени t. Известно, что при вычислении примитива V (t) функция получается R (t) который представляет собой позиция частицы против времени.
В постоянная интеграции он будет представлять значение начальной позиции, то есть в момент t = 0.
Аналогично, если функция известна В) который представляет собой ускорение частицы против времени. Примитив A (t) приведет к функции V (t), где постоянная интеграции будет значением начальной скорости V0.
в экономия, получая посредством интегрирования примитив функции стоимости. В постоянная интеграции будут представлять собой постоянные затраты. И так много других приложений, заслуживающих дифференциального и интегрального исчисления.
Как рассчитывается постоянная интегрирования?
Для расчета постоянная интегрирования, всегда будет необходимо знать первоначальные условия. Которые отвечают за определение того, какой из возможных примитивов является соответствующим.
Во многих приложениях он рассматривается как независимая переменная в момент времени (t), где постоянная C принимает значения, которые определяют первоначальные условия конкретного случая.
Если взять исходный пример: ∫ (2x + 1) dx = x2 + х + C
Допустимое начальное условие может заключаться в том, что график проходит через определенную координату. Например, известно, что примитив (x2 + х + C) проходит через точку (1, 2)
F (х) = х2 + х + C; это общее решение
F (1) = 2
Подставим в это равенство общее решение
F (1) = (1)2 + (1) + С = 2
Отсюда легко следует, что C = 0
Таким образом, соответствующий примитив для этого случая есть F (х) = х2 + х
Есть несколько типов числовых упражнений, которые работают с константы интегрирования. Фактически, дифференциальное и интегральное исчисление не перестают применяться в современных исследованиях. Их можно найти на разных академических уровнях; от первоначального расчета, через физику, химию, биологию, экономику и другие.
Это также видно при изучении дифференциальные уравнения, где постоянная интеграции Он может принимать разные значения и решения, это связано с многочисленными производными и интеграциями, которые выполняются в этом вопросе.
Примеры
Пример 1
- Пушка высотой 30 метров стреляет вертикально вверх. Известно, что начальная скорость снаряда составляет 25 м / с. Принимать решение:
- Функция, определяющая положение снаряда по времени.
- Время полета или момент, когда частица падает на землю.
Известно, что при прямолинейном движении, равномерно изменяющемся, ускорение является постоянной величиной. Это случай запуска снаряда, где ускорение будет равным гравитации.
g = — 10 м / с2
Также известно, что ускорение — это вторая производная от положения, что указывает на двойное интегрирование в разрешении упражнения, таким образом, получая два константы интегрирования.
А (т) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
Начальные условия упражнения указывают на то, что начальная скорость равна V0 = 25 м / с. Это скорость в момент времени t = 0. Таким образом выполняется следующее:
V (0) = 25 = -10 (0) + C1 Y C1= 25
С определенной функцией скорости
V (t) = -10t + 25; Сходство с формулой MRUV (VF = V0 + а х т)
Аналогичным образом мы продолжаем интегрировать функцию скорости, чтобы получить выражение, определяющее положение:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5t2 + 25т + C2
R (t) = -5t2 + 25т + C2 (примитив позиции)
Начальное положение R (0) = 30 м известно. Затем вычисляется конкретный примитив снаряда.
R (0) = 30 м = -5 (0)2 + 25(0) + C2 . куда C2 = 30
Первый раздел разрешен, так как R (t) = -5t2 + 25т + 30 ; Это выражение гомологично формуле смещения в MRUV R (t) = R0 + V0т — гт2/2
Для второго раздела необходимо решить квадратное уравнение: -5t2 + 25т + 30 = 0
Поскольку это заставляет частицу достигнуть земли (позиция = 0)
Фактически, уравнение 2-й степени дает нам 2 решения T: {6, -1}. Значение t = -1 игнорируется, потому что это единицы времени, домен которых не включает отрицательные числа.
Таким образом решается второй участок, где время полета равно 6 секундам.
Пример 2
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (x) = 4; f ‘(2) = 2; f (0) = 7
Когда информация о второй производной f ’’ (x) = 4, начинается процесс антидеривации.
f ’(x) = ∫f’ ’(x) dx
∫4 dx = 4x + C1
Затем, зная условие f ‘(2) = 2, переходим:
4 (2) + С1 = 2
C1 = -6 и f ’(x) = 4x — 8
Проделайте то же самое для второго постоянная интеграции
f (x) = ∫f ’(x) dx
∫ (4x — 
Начальное условие f (0) = 7 известно и приступаем:
2(0)2 — 8 (0) + С2 = 7
C2 = 7 и f (x) = 2x2 — 8x + 7
- f ’’ (x) = x2 ; f ‘(0) = 6; f (0) = 3
Аналогично предыдущей задаче мы определяем первые производные и исходную функцию из начальных условий.
f ’(x) = ∫f’ ’(x) dx
∫ (х2) dx = (x3/ 3) + С1
При условии f ‘(0) = 6 переходим:
( 03/ 3) + С1 = 6; куда1 = 6 и f ’(x) = (x3/3 ) + 6
Затем второй постоянная интеграции
f (x) = ∫f ’(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + С2
Начальное условие f (0) = 3 известно и приступаем:
[(0)4/ 12] + 6 (0) + C2 = 3; куда2 = 3
Таким образом, мы получаем примитивное частное
f (x) = (Икс4/ 12) + 6x + 3
Пример 3
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = 2x — 2, который проходит через точку (3, 2)
Важно помнить, что производные относятся к наклону линии, касательной к кривой в данной точке. Где некорректно предполагать, что график производной касается указанной точки, поскольку она принадлежит графику примитивной функции.
Таким образом, мы выражаем дифференциальное уравнение следующим образом:
dy = (2х — 2) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (2x — 2) dx
у = х2 — 2x + C
Применение начального условия:
2 = (3)2 — 2 (3) + С
С = -1
Получается: f (х) = х2 — 2х — 1
- dy / dx = 3x2 — 1, который проходит через точку (0, 2)
Выразим дифференциальное уравнение следующим образом:
dy = (3x2 — 1) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (3x2 — 1) дх
у = х3 — х + С
Применение начального условия:
2 = (0)2 — 2 (0) + С
С = 2
Получается: f (х) = х3 — х + 2
Предлагаемые упражнения
Упражнение 1
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (х) = х; f ‘(3) = 1; f (2) = 5
- е » (х) = х + 1; f ‘(2) = 2; f (0) = 1
- f » (x) = 1; f ‘(2) = 3; f (1) = 10
- е » (х) = -х; f ‘(5) = 1; f (1) = -8
Упражнение 2.
- Воздушный шар, поднимающийся со скоростью 16 футов / с, сбрасывает мешок с песком с высоты 64 футов над уровнем земли.
- Определите время полета
- Что будет вектор VF когда я упаду на пол?
Упражнение 3.
- На рисунке показан график ускорения-времени автомобиля, движущегося в положительном направлении оси x. Автомобиль двигался с постоянной скоростью 54 км / ч, когда водитель нажал на тормоза и остановился за 10 секунд. Определите:
- Начальный разгон автомобиля
- Скорость автомобиля при t = 5с
- Смещение автомобиля при торможении
Упражнение 4.
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = x, проходящий через точку (-1, 4)
- dy / dx = -x2 +1, который проходит через точку (0, 0)
- dy / dx = -x + 1, который проходит через точку (-2, 2)
Ссылки
- Интегральное исчисление. Неопределенный интеграл и методы интегрирования. Уилсон, Веласкес Бастидас. Университет Магдалены 2014
- Стюарт, Дж. (2001). Расчет переменной. Ранние трансцендентальные. Мексика: Thomson Learning.
- Хименес, Р. (2011). Математика VI. Интегральное исчисление. Мексика: Pearson Education.
- Физика И. Мак Гроу Хилл
План урока:
Криволинейная трапеция и понятие определенного интеграла
Формула Ньютона-Лейбница
Задачи, связанные с определенным интегралом
Криволинейная трапеция и понятие определенного интеграла
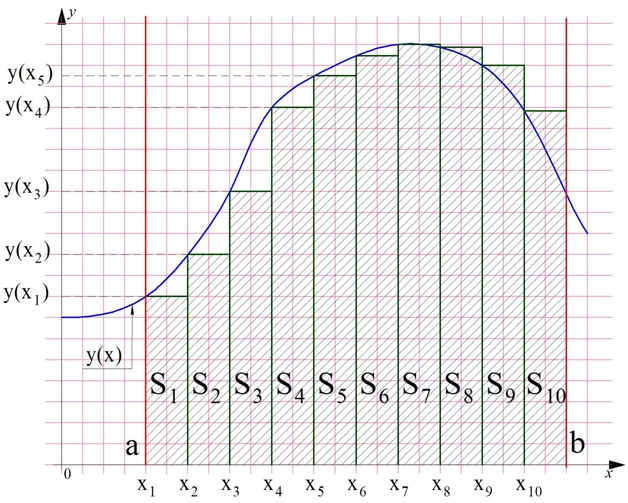
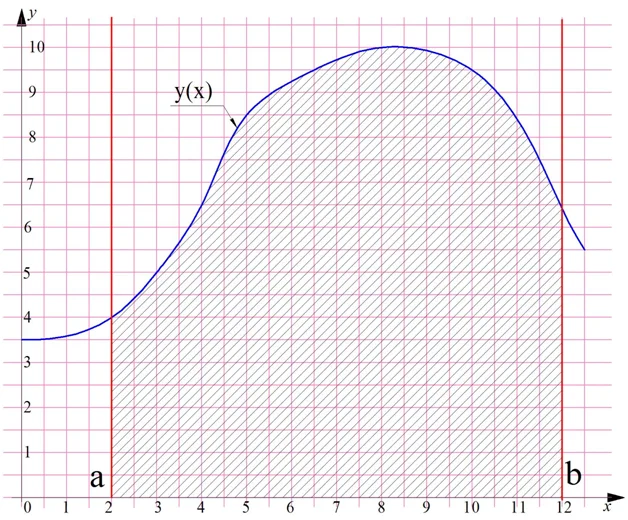
Построим на плоскости график произвольной функции у(х), который полностью располагается выше горизонтальной оси Ох. Далее проведем две вертикальные линии, пересекающие ось Ох в некоторых точках a и b. В результате мы получим интересную фигуру, которая на рисунке показана штриховкой:
Особенностью этой фигуры является то, что одна из ее сторон (верхняя) – это не прямая линия, а какая-то произвольная кривая. Условно будем считать эту фигуру четырехугольником, ведь у нее действительно четыре угла и четыре стороны. Две из них (вертикальные красные линии), очевидно, параллельны друг другу. Две другие стороны (кривую линию и участок оси Ох) параллельными назвать никак нельзя.
Напомним, что в геометрии четырехугольник, у которого две стороны параллельны друг другу, а две другие не параллельны, называют трапецией. Поэтому полученную нами фигуру мы также назовем трапецией. Но так как одна из ее сторон кривая, то мы будем использовать термин «криволинейная трапеция», чтобы отличать ее от трапеции «настоящей».
У каждой плоской фигуры есть площадь, и криволинейная трапеция – не исключение. Но как ее подсчитать? Есть приближенный способ подсчета. Разобьем отрезок [a; b] на несколько более мелких отрезков, и построим на каждом из них прямоугольник:
Обозначим площадь первого прямоугольника как S1, площадь второго прямоугольника – как S2 и т. д. Мы строим прямоугольники таким образом, что их левая сторона в точности равна значению функции в соответствующей точке. Обозначим те точки, на которых стоят стороны прямоугольника, как х1, х2, х3 и т. д. Тогда значения функции в этих точках будут соответственно равны у(х1), у(х2) и т. д.:
Площадь каждого полученного прямоугольника подсчитать несложно – она равна произведению его высоты на ширину. Мы организовали разбиение на прямоугольники таким образом, что ширина у них одинакова. Обозначим ее как ∆х. Тогда площадь каждого отдельного прямоугольника равна
Тогда общая площадь криволинейной трапеции приближенно будет равна сумме площадей всех треугольников:
где n – это количество прямоугольников (на рисунках мы выбрали n = 10).
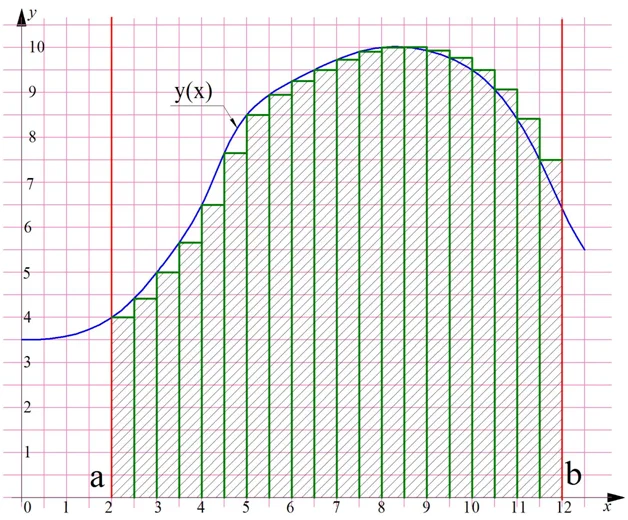
Ясно, что чем больше число n, тем более точное приближение мы получим. Например, если разбить трапецию уже не на 10, а на 20 прямоугольников, то получим такую картинку:
Обратите внимание, что ширина каждого прямоугольника, то есть величина ∆х, уменьшилась.
При росте числа n ошибка при оценке площади трапеции будет уменьшаться и стремится к нулю. Поэтому в предельном случае, когда n стремится к бесконечности, в формуле (1) вместо знака приближенного равенства «≈» можно поставить знак «=». При этом величина ∆х также будет стремится к нулю, то есть становится бесконечно малой. В математике для таких величин вместо символа ∆ принято использовать букву d, то есть вместо ∆х мы напишем dx. С учетом всего этого формула (1) примет вид:
В правой части стоит сумма бесконечного числа слагаемых. У нее есть специальное название – определенный интеграл. Ясно, что величина этой суммы, то есть площадь трапеции, зависят от чисел а и b (боковых границ трапеции). Поэтому обозначение интеграла выглядит так:
Обозначение очень похоже на неопределенный интеграл. Единственное отличие – это появление чисел а и b, которые определяют боковые границы трапеции. Число b называют верхним пределом интегрирования, а число a– нижним пределом интегрирования. Дадим более строгое определение понятию определенного интеграла.
Геометрический смысл определенного интеграла заключается в том, что он равен площади криволинейной трапеции, ограниченной графиком функции у(х) и вертикальными прямыми, проходящими через точки а и b.
Формула Ньютона-Лейбница
Изначально мы хотели научиться вычислять площадь криволинейной трапеции, однако пока что мы лишь придумали, как ее обозначать – через определенный интеграл. Но как вычислить значение его значение? Оказывается, определенный интеграл очень тесно связан с неопределенным интегралом, и эта связь описывается формулой Ньютона-Лейбница.
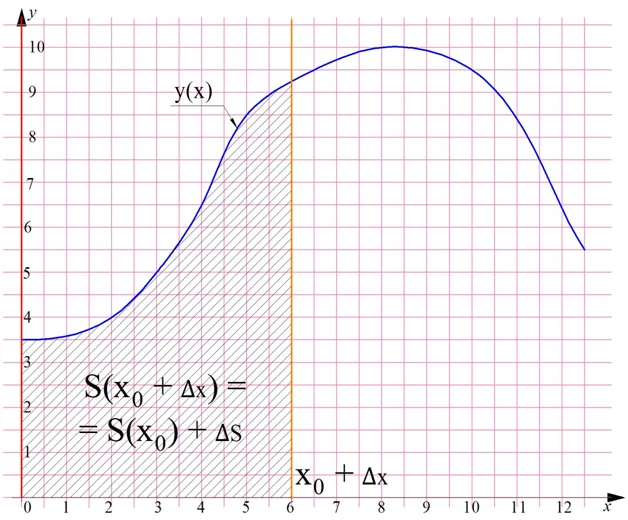
Ещё раз построим криволинейную трапецию, а ее площадь обозначим как S. Пусть ее левая граница совпадает с осью Оу, а правая будет равна некоторому значению х0. Дело в том, что нас будет интересовать зависимость площади трапеции от значения ее правой границы, то есть некоторая функция S(x). Обозначим площадь получившейся трапеции как S(x0):
Теперь сдвинем правую границу вправо на величину ∆х. В итоге получим новую трапецию, площадь которой можно записать как S(x0 + ∆x). При этом ее площадь увеличилась на некоторую величину ∆S:
Получается, что мы дали некоторое приращение аргумента ∆х, и получили приращение функции ∆S. Мы уже выполняли похожие действия в рамках предыдущих уроков, изучая понятие производной.
Итак, мы можем записать, что
Оценим величину ∆S. Если заменить соответствующую площадь прямоугольником, то его площадь окажется равной произведению ширины прямоугольника (она равна ∆x) на высоту, которая равна у(х0):
Поделим обе части равенства (2) на величину ∆х и получим:
А теперь устремим величину ∆х к нулю. В результате в равенство (2), а значит, и (3) будет становиться все более точным. В итоге мы можем написать, что
Хорошо подумайте, что мы получили. Вспомните определение производной. Оказывается, в левой части равенства (4) стоит не что иное, как производная функции S! То есть мы можем написать, что
Получается, что производная функции S на равна значению функции у(х). А это значит, что она является ее первообразной:
Здесь F(x) – первообразная функции у(х), а F(x0) – конкретное значение этой первообразной в точке х0.
Теперь рассмотрим более привычную криволинейную трапецию, у которой правой и левой границей являются числа а и b:
Как найти ее площадь? С помощью формулы (5) мы можем найти две площади:
Из рисунков очевидно, что площадь интересующей нас трапеции равна разности величин S(b) и S(a):
Эту площадь мы и обозначаем определенным интегралом. То есть можно записать, что
Таким образом, чтобы найти площадь криволинейной трапеции, необходимо проинтегрировать функцию у(х), а потом в полученную первообразную подставить числа а и b вычесть один результат из другого.
Для примера вычислим площадь криволинейной трапеции, ограниченной линией у = х2 и вертикальными прямыми х = 1 и х = 3.
Сначала находим первообразную функции у = х2, взяв от нее интеграл (неопределенный):
Отметим, что в обоих случаях речь идет об одной и той же первообразной, поэтому значения констант С у них одинаковы. Теперь вычитаем из F(3) величину F(1):
Константы интегрирования сократились. Для простоты решение записывают в несколько более короткой форме. Сначала сразу после определенного интеграла пишут первообразную (то есть находят неопределенный интеграл), причем без константы интегрирования
Далее ставят вертикальную черту и пишут пределы интегрирования, которые надо подставить в первообразную:
Потом ставят знак равно и подставляют в первообразную верхнее и нижнее число, после чего выполняют оставшиеся арифметические действия:
Задание. Вычислите
Задание. Найдите площадь фигуры, ограниченной полуволной синусоиды и осью Ох.
Решение. Сначала построим схематичный график у = sinx, чтобы понять, что именно нам надо вычислить:
Теперь ясно, что надо произвести вычисление определенного интеграла синуса на отрезке [0; π]:
Итак, мы теперь знаем и про определенный, и про неопределенный интеграл. Хотя они и очень похожи, между ними есть большая разница, и ее важно понимать. Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции. Формула Ньютона-Лейбница как раз и показывает ту связь, которая есть между двумя этими различными понятиями.
Может ли определенный интеграл быть отрицательным числом? Кажется, что нет, ведь площадь фигур не бывает отрицательной. Но не всё так просто. Рассмотрим случай, когда график функции является не верхней, а нижней границей трапеции. Например, пусть трапеция образована функцией
Просто надо найти определенный интеграл:
Получили отрицательное значение. Дело в том, что фигура располагается под осью Ох. Из-за этого ее площадь получается со знаком минус.
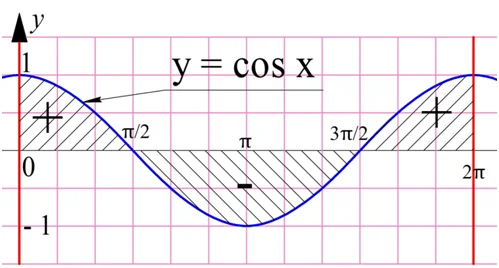
Рассмотрим ещё один пример. Найдем интеграл косинуса на промежутке от 0 до 2π:
Получился ноль. Посмотрим на графике, какую же площадь мы посчитали:
Оказывается, график на отрезке дважды пересекает ось Ох. В результате получается сразу три криволинейных трапеции. Две из них расположены выше оси Ох, а потому из площади считаются со знаком «+». Третья трапеция лежит ниже оси Ох, а потому ее площадь считается со знаком «–». То, что интеграл оказался равным нулю, означает, что площадь нижней трапеции в точности равна сумме площадей двух верхних фигур, поэтому в сумме они и дали ноль.
Отметим важное свойство определенного интеграла:
Проиллюстрируем это правило графически. Каждый из этих интегралов равен площади соответствующих криволинейных трапеций:
Задачи, связанные с определенным интегралом
Определенный интеграл помогает находить и площади более сложных фигур, которые получаются при пересечении нескольких различных графиков.
Рассмотрим задачу на интеграл. Пусть требуется найти площадь фигуры, полученной при пересечении параболы
Сначала найдем точки пересечения графиков. Для этого приравняем функции:
Корнями этого квадратного уравнения являются числа 1 и 4. Именно в этих точках и пересекаются графики (это и так видно из графика). Площадь интересующей нас фигуры можно получить вычитанием из одной криволинейной трапеции другой:
Величины S1и S2 можно вычислить через определенный интеграл. Обратите внимание, что найденные нами корни являются пределами интегрирования:
Тогда искомая нами площадь составит
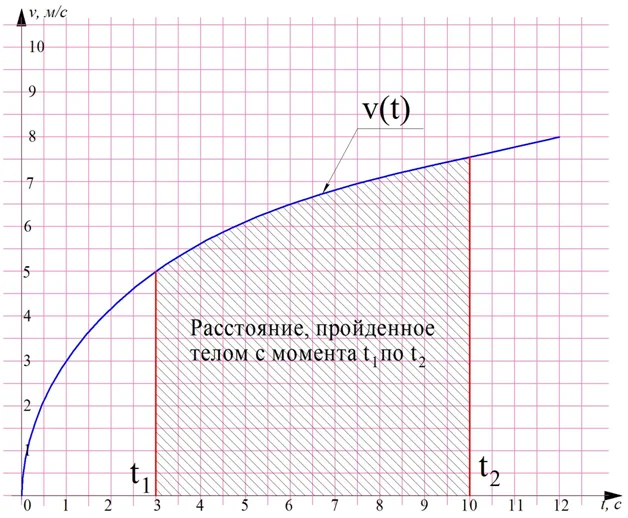
Ошибочно думать, что определенные интегралы нужны только для расчета площадей. С их помощью можно и решать ряд физических задач. Пусть известен закон изменения скорости тела v(t). Можно доказать, что путь, пройденный этим телом за период времени с t1по t2, будет равен интегралу
Задание. Самолет разгоняется, однако из-за сопротивления воздуха он набирает скорость не равномерно. Скорость самолета в момент времени t может быть вычислена по формуле
Определите, какое расстояние пролетит самолет в период времени между 16-ой и 25-ой секундой разгона.
Решение. Задача сводится к простому вычислению интеграла:
Ответ: 610 метров.
Этот пример показывает важную зависимость между скоростью тела и путем, который она преодолевает. Если есть график изменения скорости тела, то площадь под этим графиком равна тому пути, которое проходит тело:
Действительно, если тело двигается равномерно (то есть с постоянной скоростью), то путь, пройденный им, может быть вычислен по известной формуле
Но если построить для такого случая график v(t), то он будет выглядеть как горизонтальная прямая линия. Тогдафигура под графиком окажется прямоугольником, чья площадь равна произведению длины и ширины:
Заметим, что зависимость между путем, скоростью временем носит линейный характер, и именно поэтому здесь может быть использован неопределенный интеграл. Но ведь в физике очень много линейных зависимостей! И во всех этих случаях интегралы играют огромную роль!
Рассмотрим задачу. Есть пружина, которая изначально находится в нерастянутом состоянии. Потом человек начинает медленно и с постоянной скоростью, растягивать пружину, увеличивая ее длину на 0,5 метра. Жесткость пружины (ее коэффициент упругости) равна 100 Н/м. Какую работу совершил человек при растягивании пружины?
Из средней школы известна следующая формула для вычисления работы:
где F– сама сила, а S– путь, пройденный телом под действием этой силы. Легко заметить, что эта формула похожа на ранее рассмотренную зависимость пути от скорости и времени (они обе являются линейными). Сначала рассмотрим простой случай, когда сила остается неизменной. Тогда можно построить график F(S). Окажется, что площадь под графиком как раз равна работе, совершенной силой:
Случай с пружиной сложнее, ведь сила при растяжении пружины не остается неизменной. Чем сильнее растянута пружина, с тем большей силой ее приходится тянуть. Известен закон Гука, связывающий удлинение пружины с силой ее натяжения:
где k – коэффициент жесткости пружины, а x– ее удлинение. По смыслу задачи максимальное удлинение известно и равно 0,5 м. Можно нарисовать такой график зависимости силы натяжения пружины от ее удлинения (он будет выглядеть как прямая линия, так как эта зависимость является прямой пропорциональностью):
И в данном случае работа также будет равна площади под графиком функции, то есть ее можно посчитать с помощью определенного интеграла! В качестве пределов интегрирования надо взять крайние значения удлинения пружины (это 0 и 0,5 м), а качестве интегрируемой функции – F(t), которая равна
Существует и много других примеров приложений определенного интеграла. С его помощью можно находить объемы сложных фигур (конуса, пирамиды, тел вращения), определять центр масс тел сложной формы. Следует отметить и использование интегралов в механике при решении задач, в которых сила действует не на конкретную точку, а на площадь (задачи на распределенную нагрузку). В качестве примера можно привести расчет прочности крыши, на которой лежит слой снега.Но для их рассмотрения необходим более высокий уровень математических и физических знаний, который можно получить уже в рамках не среднего, а высшего образования.
Одно из самых значимых понятий в математике — интеграл. Термин часто можно встретить при решении задач по математике и физике. С помощью интеграла существенно упрощается поиск площади под кривой, пройденного пути объекта, движущегося неравномерно, массы неоднородного тела, функции по производной.
Что такое интеграл — понятие и определение
Интеграл представляет собой аналог суммы для бесконечного числа бесконечно малых слагаемых.
Интеграл является эффективным инструментом для решения задач из математического анализа. Слово «интеграл» происходит от латинского «integer», то есть «целый». Впервые это понятие ввел Иоганн Бернулли.
Разобраться в определении интеграла можно, если рассмотреть понятный график функции:
Исходя из графика, можно сделать вывод, что интегралом является сумма малых частей, которые составляют в целом рассматриваемый объект. Компоненты складываются в какую-то геометрическую фигуру. При сложении этих частей можно определить, какова ее площадь. Таким образом, пояснение для интеграла заключается в следующем: интеграл является площадью какой-то фигуры, расположенной под линией функции.
Данное понятие относится к определенному интегралу. Он определен на отрезке между точками а и b. В верхней части в качестве ограничения выступает некоторый график функции, как представлено на рисунке:
Математическая запись интеграла:
(int_{a}^{b}{f(x)dx})
где f(x) является той самой функцией, график которой ограничивает фигуру в верхней части;
a и b представляют собой пределы;
x соответствует направлению, вдоль которого построены столбцы на графике.
Процесс интегрирования является обратным дифференцированию. В том случае, когда требуется определить минимальный промежуток заданной функции, целесообразно взять от нее производную. Это объясняется тем, что производная или дифференциал являются быстрым методом поиска части чего-либо. Можно наглядно определить с помощью рисунка, что минимальная фигура, которая является частью целого, при таком числе составляющих компонентов не повторяет форму кривой функции. Таким образом, требуется уменьшить габариты таких частей, чтобы они максимально точно совпадали с графиком. Площадь наименьшего компонента фигуры будет стремиться к нулевому значению. Точность повышается с уменьшением размеров рассматриваемой части. Площадь геометрической фигуры состоит из суммы таких частей, которые стремятся к нулю. Записать это можно с помощью уравнения:
(P=lim_{Delta x_{i}rightarrow 0}sum{y_{i}Delta x_{i}})
Подробно полученное выражение можно рассмотреть на графике:
Площадь малой части фигуры определяется так же, как площадь прямоугольника. Значение Y нужно помножить на значение ΔХ. Так как фигура представляет собой совокупность малых частей, то их требуется сложить. Следует учитывать, что каждый компонент фигуры ΔХ стремится к нулевому значению. Поэтому формула, которая представлена выше, включает это условие и позволяет определить результат максимально точно.
Если обозначить количество частей ΔХ, стремящихся к бесконечности, то можно определить, что существует предел интегральной суммы, которая состоит из таких компонентов, стремящихся к нулю и к бесконечности по числу таких частей. Таким образом, правая граница фигуры, изображенной на графике, является пределом. В этом выражается геометрический смысл определенного интеграла.
Физический смысл интеграла состоит в том, что это сумма бесконечно малых величин на бесконечно большом интервале. Исходя из этого, можно определить любую величину, которая изменяется, согласно функции. К примеру, рассчитать общий путь по закону изменения скорости. Необходимость в интеграле возникла, когда потребовалось рассчитать площади каких-либо фигур и объем любых тел, выбранных произвольно.
В том случае, когда расчеты подразумевают наличие постоянной характеристики, к примеру, скорости, найти путь можно с помощью произведения этой постоянной скорости и времени. Этот же момент можно проверить при вычислении интеграла от такой функции и записи уравнения прямой. Но скорость в процессе движения может меняться. Данное изменение можно представить в виде зависимости. Тогда следует вписать граничные условия, например, в случае пути — это время, в интеграл скорости по времени. Полученное выражение будет равно площади трапеции, которая расположена под функцией скорости, что является физическим смыслом определенного интеграла.
Свойства, которыми обладает определенный интеграл:
- Когда функции f и g интегрируются на интервале [a, b], то для любых чисел (alpha) и (beta (alpha in R, beta in R)) функция (varphi(x) = alpha f(x) + beta g(x)) также интегрируема на отрезке [a, b]. Справедливо равенство: (intlimits_a^b (alpha f(x) + beta g(x)) dx = alpha intlimits_a^b f(x) dx + beta intlimits_a^b g(x) dx.label{ref1})
- Если функции f и g интегрируемы на отрезке [a, b], то функция (varphi(x) = f(x)g(x)) также интегрируема на этом отрезке.
- В том случае, когда функция f(x) интегрируема на отрезке (Delta = [a, b]) она интегрируема на любом отрезке (Delta_{1} subset Delta.)
- При функции f(x), интегрируемой на отрезке [a, b] и a < c < b, будет работать формула: (intlimits_a^b f(x) dx = intlimits_a^c f(x) dx + intlimits_c^b f(x) dx)
- При функции f, интегрируемой на отрезке [a, b] и если (c_{1}, c_{2}, c_{3}) являются любыми точками данного интервала, то (intlimits_{c_{1}}^{c_{3}} f(x) dx = intlimits_{c_{1}}^{c_{2}} f(x) dx + intlimits_{c_{2}}^{c_{3}} f(x) dx)
Термин «неопределенный интеграл» применим в ситуациях, когда требует найти площадь криволинейной трапеции, путь в соответствии с известной скоростью тела, которое движется неравномерно, и для решения других подобных задач.
Свойства, которыми характеризуется неопределенный интеграл:
- Константу можно выносить за знак интеграла: (int kf(x) dx = kint f(x) dx)
- Интеграл разности или суммы функций соответствует разности или сумме интегралов от этих функций: (int ( f(x) pm g(x) ) dx = int f(x) dx pm int g(x) dx)
- Производная интеграла определяется как выражение, находящееся под знаком интеграла: (bigg (int f(x) dx bigg )’ = f(x))
- Интеграл от производной функции равен сумме этой функции и постоянной: (int F'(x) dx = F(x) + C)
- Интеграл дифференциала функции равен сумме этой функции и постоянной интегрирования: (int df(x) dx = f(x) + C)
Таблица интегралов для студентов
Такие формулы позволяют упростить решение многих задач. Основные интегралы:
(int 0dx=C)
(int dx=int 1dx=x+C)
(int x^n dx = frac{x^{n+1}}{n+1}+C)
(int frac{dx}{x}=ln |x|+C)
(int a^x dx = frac{a^x}{ln a} + C)
(int e^x dx = e^x + C)
(int sin x dx = -cos x + C)
(int cos x dx = sin x+C)
(int frac{dx}{sin^2 x}=-ctgx + C)
(int frac{dx}{cos^2 x}=tgx+C)
(int frac{dx}{sqrt{a^2-x^2}}=arcsin frac{x}{a}+C)
(int frac{dx}{a^2+x^2}=frac{1}{a}arctgfrac{x}{a}+C)
(int frac{dx}{a^2-x^2}=frac{1}{2a} ln|frac{a+x}{a-x}|+C)
(int frac{dx}{sqrt{x^2pm a^2}}=ln|x+sqrt{x^2pm a^2}|)
Методы решения интегралов
Данные методики позволяют преобразовать сложные уравнения в простые формы, решения которых можно найти в таблице. Также к преобразованным выражениям можно применять свойства интегралов.
Непосредственное интегрирование
Данный метод целесообразно применять, когда в интеграле имеются табличные простейшие функции, либо функции, которые можно представит в таком виде по результатам элементарных действий. К примеру, когда требуется вынести константу за знак интеграла, разбить интеграл на слагаемые в виде интегралов, чтобы в подынтегральном выражении присутствовала готовая функция для интегрирования. Можно привести простой пример:
Необходимо определить интеграл непосредственным интегрированием:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx)
Исходя из свойства суммы интегралов, получим:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = int x^3 dx + int frac{3 dx}{2sqrt{x}} + int frac{2 dx}{x})
Первый интеграл записан в табличном виде. В таком случае можно воспользоваться непосредственным интегрированием:
(int x^3 dx = frac{x^{3+1}}{3+1} = frac{x^4}{4} + C)
Второй интеграл обладает константой, которую допустимо вынести за знак. Затем интеграл будет преобразован в табличную форму:
(int frac{3dx}{2sqrt{x}} = 3 int frac{dx}{2sqrt{x}} = 3 sqrt{x} + C)
В третьем интеграле можно вынести константу. Далее необходимо воспользоваться методом непосредственного интегрирования:
(int frac{2dx}{x} = 2int frac{dx}{x} = 2 ln x + C)
Полученные выражения необходимо представить в виде одной записи:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x + C)
Ответ: (int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x+ C)
Метод подведения под знак дифференциала
Решить некоторые типы интегралов можно с помощью этого способа. Он заключается в вынесении под знак интеграла. Таким образом получается интеграл табличной формы. Формула имеет следующий вид:
(f'(x) dx = d( f(x) ))
В том случае, когда подынтегральная функция содержит произведение пары функций, одна из которых представляет собой дифференциал другой, нужно внести под знак дифференциала нужную функцию. Данное действие можно записать таким образом:
(int f(varphi(x)) varphi'(x) dx = int f(varphi(x)) d(varphi(x))=int f(u) du)
(u=varphi(x))
Воспользоваться способом подведения основных функций можно при знании таблицы производных и интегрирования. Из них следуют следующие уравнения:
(dx = d(x+c) )
(c=const)
(-sin x dx=d(cos x))
(dx=frac{1}{a} d(ax))
(cos x dx = d(sin x))
(xdx=frac{1}{2} d(x^2+a) )
(frac{dx}{x} = d(ln x))
(-frac{dx}{x^2}= d(frac{1}{x}))
(frac{dx}{cos^2 x} = d(tg x))
(int f(kx+b)dx = frac{1}{k} int f(kx+b)d(kx+b) = frac{1}{k} F(kx+b) + C)
В качестве примера можно решить задачу на нахождение интеграла, обладающего таким видом:
(int sin x cos x dx)
В этом случае допустимо заносить под знак дифференциала любую из указанных функций. Целесообразно занести (cos x) из-за удобства смены знаков. Применяя формулы, получим:
(int sin x cos xdx = int sin x d(sin x) = frac{1}{2} sin^2 x + C)
Ответ: (int sin x cos x dx = frac{1}{2} sin^2 x + C)
Метод интегрирования по частям
Данная методика применима, когда требуется решить интегралы от произведения двух простейших функций. Одна из них достаточно просто дифференцируется, а вторая — интегрируется. В данном случае справедлива методика для неопределенных и определенных интегралов. Неопределенный интеграл характеризуется уравнением:
(int udv = uv — int vdu)
Определенный интеграл соответствует формуле:
(int limits_{a}^{b} udv = uv bigg |_{a}^{b} — int limits_{a}^{b} vdu)
В качестве примера можно определить интеграл:
(int xe^xdx)
Заметим, что в состав подынтегральной функции входит пара функций. Одна из них путем дифференцирования преобразуется в единицу, а вторая достаточно просто интегрируется. Поэтому в данном случае справедлив метод интегрирования по частям. Можно предположить, что:
(u = x rightarrow du=dx)
(dv = e^x dx rightarrow v=e^x)
Далее необходимо подставить полученные значения в первую формулу интегрирования:
(int xe^x dx = xe^x — int e^x dx = xe^x — e^x + C)
Ответ: (int xe^x dx = xe^x — e^x + C)
Метод замены переменной или метод подстановки
Этот способ нахождения интегралов применим в задачах, где одна функция — это производная второй функции. Допустим, что интеграл записан так:
(int f(x) dx)
Можно заменить (x=phi(t)). При этом функция (phi(t)) является дифференцируемой, поэтому можно найти (dx = phi'(t) dt.)
Далее следует подставить (begin{vmatrix} x = phi(t) \ dx = phi'(t) dt end{vmatrix}) в интеграл. Таким образом:
(int f(x) dx = int f(phi(t)) cdot phi'(t) dt)
Полученное выражение является формулой замены переменной в неопределенном интеграле.
При условиях задачи, которая содержит интеграл (int f(phi(x)) cdot phi'(x) dx), целесообразно заменить переменную на новую:
(t = phi(x))
(dt = phi'(t) dt)
Таким образом, интеграл преобразуется в форму, которую легко рассчитать с помощью основных методов интегрирования:
(int f(phi(x)) cdot phi'(x) dx = int f(t)dt)
Следует помнить, что по итогам расчетов требуется вернуть замененную переменную назад к x.
Например, можно рассмотреть задачу, по условиям которой необходимо вычислить неопределенный интеграл с помощью замены переменной:
(int e^{3x} dx)
Замена переменной будет выполнена следующим образом:
(t = 3x)
(dt = 3dx)
Таким образом:
(int e^{3x} dx = int e^t frac{dt}{3} = frac{1}{3} int e^t dt =frac{1}{3} e^t + C = frac{1}{3} e^{3x} + C)
Ответ: (int e^{3x} dx = frac{1}{3} e^{3x} + C)
Примеры решения
Задача 1
Требуется рассчитать определенный интеграл:
(int_0^1 frac{x}{x^4+1} dx)
Решение
Требуется заменить (t = x^2)
Таким образом, (dt = 2xdx)
Далее необходимо пересчитать пределы интегрирования для переменной t. Для этого нужно подставить 0 и 1 в замену (t = x^2)
В данной задаче они остались прежними. После манипуляций с подстановками получим:
(int_0^1 frac{x}{x^4+1}dx = int_0^1 frac{1}{2} frac{dt}{t^2+1})
Можно найти интеграл по таблице:
(int_0^1 frac{1}{2} frac{dt}{t^2+1}=frac{1}{2} arctg t bigg |_0^1)
Используя формулу Ньютона-Лейбница, запишем решение:
(frac{1}{2} arctg t bigg |_0^1 =frac{1}{2} arctg 1 — frac{1}{2} arctg 0 = frac{1}{2} cdot frac{pi}{4} = frac{pi}{8})
Ответ: (int_0^1 frac{x}{x^4+1} dx = frac{pi}{8})
Задача 2
Необходимо решить определенный интеграл:
(int_0^pi (x+5)sin x dx)
Решение
Можно заметить произведение двух функций, которое находится под интегралом. В этом случае целесообразно воспользоваться методом интегрирования по частям:
(int udv = uv — int vdu)
(int_0^pi (x+5) sin x dx = begin{vmatrix} u = x+5 & du = dx \ dv = sin x dx & v = -cos x end{vmatrix})
Нужно подставить в уравнение интегрирования по частям рассчитанные данные из вертикальных скобок:
(-(x+5)cos x bigg |_0^pi + int_0^pi cos x dx)
С помощью формулы Ньютона-Лейбница для вычисления определенного интеграла запишем ответ:
(-(x+5)cos x bigg |_0^pi + int_0^pi cos x dx = -(pi+5) cdot (-1) + 5 + sin x bigg |_0^pi = pi + 10 + sin pi — sin 0 = pi + 10)
Ответ: (int_0^pi (x+5)sin x dx = pi + 10)
Задача 3
Требуется найти определенны интеграл, записанный в виде:
(int_0^2 (x^3 + 2x + 2) dx)
Решение
Используя способ разложения интеграла на простейшие, после получения промежуточного результата необходимо интегрировать каждый интеграл индивидуально:
(int_0^2 (x^3+2x+2) dx = int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx)
В случае первых двух интегралов целесообразно воспользоваться правилом:
(x^p = frac{x^{p+1}}{p+1})
Третий интеграл содержит константу. Таким образом:
(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )
Далее следует подставить пределы интегрирования в каждую функцию и записать ответ:
(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )
Ответ: (int_0^2 (x^3 + 2x + 2) dx = 12)
Задача 4
Необходимо найти решение интеграла:
(int 3cos x dx)
Решение
Требуется вынести константу по первому свойству за знак интеграла и записать ответ:
(int 3cos x dx = 3 int cos x dx = 3 sin x + C)
Ответ: (int 3cos x dx = 3 sin x + C)
Задача 5
Необходимо определить интеграл:
(int (e^x + sin x) dx)
Решение
Исходя из первого свойства неопределенного интеграла, интеграл суммы равен сумме интегралов:
(int (e^x + sin x) dx = int e^x dx + int sin x dx = e^x — cos x)
Ответ: (int (e^x + sin x) dx = e^x — cos x)
Задача 6
Требуется определить производную от интеграла:
( int ln x dx)
Решение
Согласно третьему свойству неопределенного интеграла, производная неопределенного интеграла определяется, как подынтегральная функция:
(bigg (int ln x dx bigg )’ = ln x)
Ответ: (bigg (int ln x dx bigg )’ = ln x)
Задача 7
Требуется доказать следующее выражение:
( int (x^2+x)’ = x^2+x+C)
Решение
В первую очередь необходимо определить производную подынтегральной функции:
( (x^2+x)’ = (x^2)’ + (x)’ = 2x + 1)
Исходя из первого и второго свойства неопределенного интеграла, получим ответ:
(int (2x+1) dx = int 2x dx + int 1 dx = 2 int x dx + int 1 dx =2 cdot frac{x^2}{2} + x + C = x^2 + x + C)
Ответ: выражение доказано.
Благодаря теоретическим знаниям и практическим навыкам решения задач с интегралами, можно с легкостью осваивать самые сложные темы по физике и математическому анализу. Главное — уметь пользоваться таблицей с основными формулами и свойствами определенного и неопределенного интегралов. Если в процессе изучения материала возникают трудности, то в любое время можно открыть сервис Феникс.Хелп.
В исчислении , то константа интегрирования , часто обозначается , является термин константы добавляется к первообразной функции , чтобы указать , что неопределенный интеграл от (то есть, в совокупности всех первообразных в ), на связную области , определяется только до к аддитивной константе. Эта константа выражает неоднозначность, присущую конструкции первообразных.
Более конкретно, если функция определена на интервале и является первообразной от , то набор всех первообразных задается функциями , где — произвольная константа (что означает, что любое значение будет составлять действительную первообразную). По этой причине неопределенный интеграл часто записывается как , хотя константа интегрирования может иногда опускаться в списках интегралов для простоты.
Источник
Производная любой функции постоянной равна нулю. После того, как кто-то нашел одну первообразную для функции , добавление или вычитание любой константы даст нам другую первообразную, потому что . Константа — это способ выразить, что каждая функция, по крайней мере, с одной первообразной, будет иметь их бесконечное количество.
Позвольте и быть двумя всюду дифференцируемыми функциями. Предположим, что для каждого действительного числа x . Тогда существует действительное число такое, что для любого действительного числа x .
Чтобы доказать это, обратите внимание на это . So может быть заменен на и на постоянную функцию , чтобы доказать, что всюду дифференцируемая функция, производная которой всегда равна нулю, должна быть постоянной:
Выбери реальное число , и пусть . Для любого х , в основной теоремы исчисления , вместе с предположением , что производная обращается в нуль, следует , что
тем самым показывая, что это постоянная функция.
Два факта имеют решающее значение в этом доказательстве. Сначала подключается настоящая линия . Если бы реальная линия не была подключена, мы не всегда могли бы интегрировать от фиксированного a до любого заданного x . Например, если бы мы попросили функции, определенные на объединении интервалов [0,1] и [2,3], и если бы a было равно 0, то было бы невозможно интегрировать от 0 до 3, потому что функция не определен между 1 и 2. здесь будет две константы, по одному для каждого подключенного компонента в домене . В общем, заменяя константы локально постоянными функциями , мы можем распространить эту теорему на несвязные области. Например, есть две постоянные интегрирования для и бесконечно много для , поэтому, например, общая форма интеграла от 1 / x такова:
Во-вторых, и предполагалось, что они всюду дифференцируемы. Если и не дифференцируемы хотя бы в одной точке, то теорема может потерпеть неудачу. В качестве примера, пусть будет ступенчатая функция Хевисайда , которая равна нулю для отрицательных значений x и единице для неотрицательных значений x , и let . Тогда производная от равна нулю там, где она определена, и производная от всегда равна нулю. Однако ясно, что и не отличаются на константу, даже если предположить, что и всюду непрерывны и почти всюду дифференцируемы, теорема все равно неверна. В качестве примера возьмем быть функция Кантора и снова пусть .
Например, предположим, что кто-то хочет найти первообразные . Одним из таких первообразных является . Еще один . Третий . У каждого из них есть производные , поэтому все они являются первообразными .
Оказывается, сложение и вычитание констант — единственная гибкость, которая у нас есть при нахождении различных первообразных одной и той же функции. То есть все первообразные с точностью до константы одинаковы. Чтобы выразить этот факт , мы пишем:
Замена на номер даст первообразную. Однако записывая вместо числа, можно получить компактное описание всех возможных первообразных . называется постоянной интегрирования . Легко определить, что все эти функции действительно являются первообразными :
Необходимость
На первый взгляд может показаться, что константа не нужна, так как ее можно обнулить. Более того, при вычислении определенных интегралов с использованием основной теоремы исчисления константа всегда сокращается сама с собой.
Однако попытка установить константу равной нулю не всегда имеет смысл. Например, может быть интегрирован как минимум тремя различными способами:
Таким образом, установка на ноль может оставить константу. Это означает, что для данной функции не существует «простейшей первообразной».
Другая проблема с установкой равного нулю состоит в том, что иногда мы хотим найти первообразную, которая имеет заданное значение в данной точке (как в задаче начального значения ). Например, чтобы получить первообразную , имеющую значение 100 при x = π, тогда будет работать только одно значение (в данном случае ).
Это ограничение можно перефразировать на языке дифференциальных уравнений . Нахождение неопределенного интеграла функции аналогично решению дифференциального уравнения . Любое дифференциальное уравнение будет иметь множество решений, и каждая константа представляет собой уникальное решение корректной задачи с начальным значением . Наложение условия, что наша первообразная принимает значение 100 при x = π, является начальным условием. Каждому начальному условию соответствует одно и только одно значение , поэтому без него решить задачу было бы невозможно.
Есть еще одно оправдание, исходящее из абстрактной алгебры . Пространство всех (подходящих) действительных функций на действительных числах является векторным пространством , а дифференциальный оператор — линейным оператором . Оператор переводит функцию в ноль тогда и только тогда, когда эта функция постоянна. Следовательно, ядро из пространства всех функций постоянных. Процесс неопределенного интегрирования сводится к поиску прообраза заданной функции. Для данной функции нет канонического прообраза, но набор всех таких прообразов формирует смежный класс . Выбор константы аналогичен выбору элемента смежного класса. В этом контексте решение задачи начального значения интерпретируется как лежащее в гиперплоскости, заданной начальными условиями .
использованная литература
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Нижний предел интегрирования стандартно обозначается буквой . Верхний предел интегрирования стандартно обозначается буквой
. …и мы выполним все пункты от «а» до «бэ» =) (c) Отрезок
называют отрезком интегрирования.
И перед тем, как перейдём к практике, небольшое faq по теме:
Что такое определенный интеграл? С формальной точки зрения, определённый интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число:
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти это число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу перепишите на листок и наклейте на самом видном месте!
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа
в определенном интеграле не добавляется. Обозначение
является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись
? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность . Готово.
Вопрос следующий, а на самом деле первый: всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования
не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример:
. Такого интеграла тоже не существует, так как в точках
,
отрезка
не существует тангенса. Желающие могут сразу ознакомиться с Приложением Графики основных функций и их построение и оценить ситуацию геометрически: там, где нет графика – те значения и не входят в область определения той или иной функции.
Таким образом, чтобы определенный интеграл вообще существовал, нужно чтобы подынтегральная функция была непрерывной на отрезке интегрирования. Понятие непрерывности тоже интуитивно понятно – если график можно начертить, не отрывая карандаша от бумаги, то данная функция непрерывна на этом участке.
И из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, желательно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.
В противном случае может получиться такой казус:
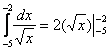
А сделать надо следующее: предварительно проверить функцию на непрерывность. И если для решения (в контрольной работе, на зачете, экзамене) вам предложен несуществующий интеграл вроде или
, то нужно дать ответ, что интеграла не существует, и обосновать, почему. Хотя, не нужно. Скорее всего, это опечатка, и преподаватель может предложить вам корректный вариант, поэтому будет хорошей идеей сразу получить консультацию на этот счёт.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим посвящена следующая глава.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике:
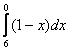
Без чего не обходится математика? Конечно же, без всевозможных свойств:

| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин


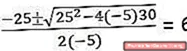











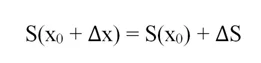












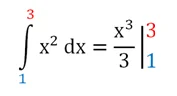













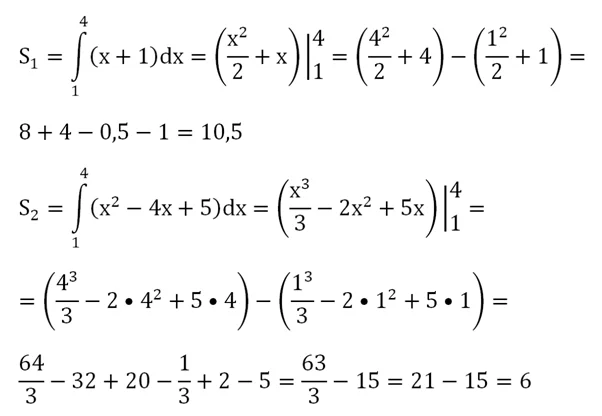






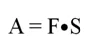














![[F (x) -G (x)] '= 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf7a4d471877352525d86a56c595661d3061ae30)

















![{ displaystyle { begin {align} { frac {d} {dx}} [ sin (x) + C] & = { frac {d} {dx}} sin (x) + { frac { d} {dx}} C \ & = cos (x) +0 \ & = cos (x) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a1f94e2f3c827cbd77d0648f1d7532f57f3a35)