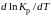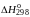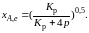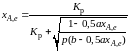Как найти константу равновесия зная температуру

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Понятие химического равновесия

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Признаки химического равновесия

1. Состояние системы остается неизменным во времени при сохранении внешних условий.
2. Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
3. Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
4. К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
5. В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Принцип Ле Шателье

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия): 

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO_(г) + O_2(г) → 2NO_2(г); ΔH^о₂₉₈ = — 113,4 кДж/моль.

Влияние температуры на химическое равновесие

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Влияние давления на химическое равновесие

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO₂. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Влияние концентрации на химическое равновесие

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O₂ вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO₂. Увеличение концентрации NO₂ смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Константа химического равновесия

Для химической реакции:

2NO_(г) + O_2(г) → 2NO_2(г)

константа химической реакции К_с есть отношение:

             К_с = [NO₂]²/([NO]² · [O₂])               (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔG_T^о = – RTlnK                      (2)

Примеры решения задач

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO _(г) + O_{2 (г)}→2CO_{2 (г)} составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение.

2CO_(г) + O_2(г) →2CO_2(г)

Вещество	CO	O2	CO2
Сисходн, моль/л	0,36	0,40	0
Спрореагир,моль/л	0,16	0,08	0,16
Сравн, моль/л	0,2	0,32	0,16

Во второй строке под С_{прореагир} понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO₂, причем, С_исходн= С_{прореагир} + С_равн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H_{2 (г)} + N_{2 (г)} →2 NH_{3 (г)} при 298 К.

Решение.

ΔG₂₉₈^о = 2·(- 16,71) кДж = -33,42·10³ Дж.

ΔG_T^о = — RTlnK.

lnK = 33,42·10³/(8,314× 298) = 13,489. K = 7,21× 10⁵.

Задача 3. Определите равновесную концентрацию HI в системе

H_2(г) + I_2(г)  →2HI_(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂ , I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H_2.

Вещество	H2	I2	HI
сисходн., моль/л	1	2	0
спрореагир., моль/л	x	x	2x
cравн., моль/л	1-x	2-x	2x

Тогда,  К = (2х)²/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H_2(г) + HCOH_(г) →CH₃OH_(г) становится равной 1. Принять, что ΔН^о_Т » ΔН^о₂₉₈, а ΔS^о_T » ΔS^о₂₉₈.

Решение.

Если К = 1, то ΔG^о_T = — RTlnK = 0;

ΔG^о_T = ΔН^о₂₉₈ — ТΔ S^о₂₉₈ .

ΔН^о₂₉₈ = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10³ Дж;

ΔS^о₂₉₈ = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52) 

Т = 786,15К

Задача 5. Для реакции SO_2(Г) + Cl_2(Г)  →SO₂Cl_2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO₂Cl₂, если исходные концентрации SO₂, Cl₂ и SO₂Cl₂ равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO_2.

SO_2(г) + Cl_2(г) →SO₂Cl_2(г)

Вещество	SO2	Cl2	SO2Cl2
cисходн., моль/л	2	2	1
cпрореагир., моль/л	x	x	х
cравн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)² = 4

Решая это уравнение, находим: x₁ = 3 и x₂ = 1,25. Но x₁ = 3 не удовлетворяет условию задачи.

Следовательно, [SO₂Cl₂] = 1,25 + 1 = 2,25 моль/л.

Задачи для самостоятельного решения

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH_{3 (г)} → 3H_{2 (г)} + N_{2 (г)}

2) ZnCO_{3 (к)} → ZnO_(к) + CO_{2 (г)}

3) 2HBr _(г) → H_{2 (г)} + Br_{2 (ж)}

4) CO_2 (г) + C _{(графит)}  →2CO _(г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr _(г)  →H_{2 (г)} + Br_{2 (г)}

составляли: [HBr] = 0,3 моль/л, [H₂] = 0,6 моль/л, [Br₂] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H_2(г) + S_(г)  →H₂S_(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H₂ и S, если исходные концентрации H₂, S и H₂S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO_2(г) + C_{(графит)}  →2CO_(г)

становится равной 1. Примите, что ΔН^о_Т≈ΔН^о₂₉₈, а ΔS^о_T≈ΔS^о₂₉₈

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С₂Н_4(г)  →С₂Н_2(г) + Н_2(г) при 298 К

6. Для реакции 2С₃Н_8(г) → н-С₅Н_12(г)+СН_4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО_2(г) + 3Н_2(г)  → СН₃ОН_(г) + Н₂О_(г)

равна 3,4·10^-5. Вычислите Δ G^о₅₀₀.

8. При температуре 800 К константа равновесия процесса н-С₆Н_14(г)+  2С₃Н_6(г)+Н_2(г) равна 8,71. Определите ΔG^о_f,800(С₃Н_6(г)), если ΔG^о_f,800(н-С₆Н_14(г)) = 305,77 кДж/моль.

9. Для реакции СО_(г) + Cl_2(г)  →СO₂Cl_2(г) при некоторой температуре равновесная концентрация СO₂Cl_2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО_(г) и Cl_2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО_2(г) + О_2(г)  →2SO_3(г) составляли: [SО₂ ]=0,10 моль/л, [О₂]=0,16 моль/л, [SО₃]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО₂ и О₂.

К=4,0; исходная концентрация SО2 составляет 0,18 моль/л; исходная концентрация О2 составляет 0,20 моль/л.

Функциональная
зависимость константы равновесия от
температуры при постоянном давлении
передается уравнением изобары
Вант-Гоффа

(2.9)

где ∆H°
– изменение энтальпии при стандартном
состоянии.

Из
уравнения (2.9) следует, что при положительных
значениях ∆H° (эндотермические
реакции)

>0
и К_р(Т)
– возрастающая функция. Если ∆H° < 0
(экзотермические реакции), то

 < 0
и константа равновесия уменьшается
с повышением температуры. В обоих
случаях равновесные концентрации
участников реакции меняются, т. е.
анализ уравнения показывает, что оно в
количественной форме отражает вывод,
вытекающий из принципа смещения
равновесия: повышение температуры
всегда смещает равновесие в направлении
эндотермической реакции.

Для
процессов, протекающих при постоянном
объеме, зависимость константы равновесия
от температуры передается уравнением
изохоры Вант-Гоффа

,

где ∆U° – изменение внутренней
энергии в стандартном состоянии.

Уравнения
изобары и изохоры реакции определяют
зависимость константы равновесия от
температуры в дифференциальной форме.
Для практических расчетов равновесия
при различных температурах требуется
провести интегрирование этих уравнений.
Если ∆H° не зависит от температуры
(это справедливо для узкого интервала
температур), то из выражения (2.9) получаем

по которому, располагая данными о ∆Н°
и К_р
для какой-либо одной температуры
Т₁
можно легко определить значение константы
равновесия при другой температуре Т₂.

Интегрируя
уравнение (2.9) при условии независимости
теплового эффекта от температуры, можно
вынести ∆Н° из-под знака интеграла
и получить следующее уравнение:

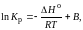
где В – постоянная интегрирования.

Так как
согласно уравнению изотермы Вант-Гоффа

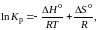
то В = ∆S°/R (при условии независимости
∆Н° и ∆S°
от температуры).

§ 2.4. Расчет равновесия по термодинамическим данным

Расчет
константы равновесия и изменения энергии
Гиббса позволяет определить равновесный
состав реакционной смеси, а также и
максимально возможное количество
продуктов.

Определение
констант равновесия химических реакций.
В основе расчета констант равновесия
для идеальных газов по термодинамическим
данным лежат уравнения (2.5) и (2.6). Эти
уравнения связывают константу равновесия
с изменением энергии Гиббса ∆G°,
зависящей от изменения энтальпии ∆Н°
и энтропии ∆S°. При этом, поскольку
важно не абсолютное значение
термодинамических функций отдельных
участников реакции, а лишь их изменение,
необходимо иметь какую-то точку отсчета.
В качестве таковой принято, что для
простых веществ (С, О₂,
Н₂ и т.
п.) в стандартных условиях и стандартном
состоянии (для газов – идеальный газ,
для жидкостей – чистая жидкость, для
твердого тела – наиболее стабильная
при данных условиях модификация)

 =
0 и

 =
0. Тогда каждое сложное соединение можно
охарактеризовать стандартной энергией
Гиббса

энтальпией

и энтропией

его образования из простых веществ.

Значения
термодинамических функций для большого
числа простых веществ и соединений
приводятся в справочной литературе.
Пользуясь справочными данными, можно
вычислить стандартные изменения энергии
Гиббса, используя правило Гесса. Так,
например, для реакции

СО₂
(г) + 4Н₂
(г)

СН₄
(г) + 2Н₂О
(г)

–394,4
0 –50,8 –228,4

значения

всех участников реакции известны и
приведены под уравнением (в кДж/моль).

Тогда
для реакции

= –50,8 – 2·228,4 + 394,4 = –113,2 кДж/моль.

Отсюда
легко рассчитать константу равновесия
при 298 К:

и,
следовательно, значение константы
равновесия при температуре процесса.

Определение
констант равновесия сложных реакций
осуществляют комбинированием простых
реакций. При этом важно выделить и учесть
каждую из составляющих простых реакций.
Комбинирование необходимо проводить
таким образом, чтобы через константы,
известные и приводимые в таблицах,
можно было выразить константы более
сложных реакций или получить по известным
константам неизвестные.

Так, для
последовательных превращений

1) А + B

R

2) R

S + Z

A + B

S + Z

константа
равновесия суммарной реакции равна
произведению констант равновесия
составляющих ее простых реакций:

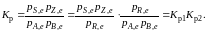
Соответственно,
суммарное изменение энергии Гиббса
равно сумме ее изменений для отдельных
реакций:

Определение
состава реакционной смеси при химическом
равновесии. Рассмотрим связь константы
равновесия K_р
и равновесной степени превращения х_a,е
для газовой реакции А

2R.

После
установления равновесия на 1 моль
введенного вещества реакционная смесь
будет содержать (1 – х_a,е)
моль реагента А и 2х_a,е
моль продукта R. Всего в равновесном
состоянии будет находиться

1 – х_a,е
+  2х_a,е
= = 1 + х_a,е
моль. Если общее давление системы в
момент равновесия равно р, можем
записать равновесные парциальные
давления компонентов согласно выражению
(2.8):

Тогда связь
между константой равновесия и равновесной
степенью превращения выразится уравнением

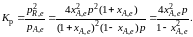
Получили
простое уравнение, из которого видно
также влияние давления: при постоянной
температуре снижение общего давления
ведет к увеличению х_a,е.
Перегруппировав это выражение, получаем

(2.10)

Расчетная
формула (2.10) позволяет найти значения
х_a,е для
разных давлений при постоянной температуре
и, следовательно, рассчитать равновесный
состав смеси. На рис. 2.1 приведена
зависимость равновесной степени
превращения реагента х_a,е
при протекании реакции А 

2R от относительного давления


= р/р₀,
где р₀
– стандартное давление, равное 0,098 МПа.

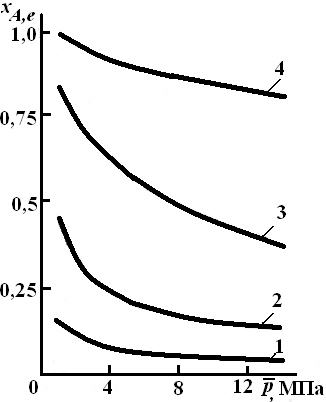
Рис.
2.1.
Зависимость равновесной степени
превращения

обратимой реакции А

2R
от давления для разных значений

константы
равновесия К_р:
1
– 0,1; 2 – 1,0; 3 – 10,0; 4 – 100,0

Пример 2.1. Рассмотрим расчет равновесия
по известным значениям K_р
для реакции окисления диоксида серы:

SO₂
+ 0,5О₂
+ zN₂

SO₃
+ zN₂,

a b n

где а, b, n – количество (моль)
компонентов исходной смеси SO₂,
O₂, N₂,
(а + b + n) = 1.

Количество
каждого компонента (моль) при достижении
равновесной степени превращения х_A,е
составит

SO₂
O₂
N₂
SO₃

а – ах_A,е
b –
0,5ах_A,е
n ах_A,е

Общее число
молей равновесной смеси

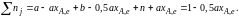
Обозначив
общее давление через р, выразим
равновесные давления компонентов:

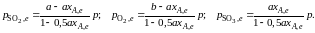
Тогда

Отсюда

.
(2.11)

Найдем
состав равновесной смеси, если в исходной
смеси содержится 7 % SO₂,
11 % О₂, 82
% N₂.

При T
= 650 К константа равновесия К_р
= 629. Подставляя исходные
данные в уравнение (2.11), получим

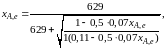
откуда находим х_A,е
= 0,994 и, следовательно, в равновесной
смеси содержится (моль): SO₃
– 0,069, SO₂
– 0,001, О₂
– 0,076, N₂
– 0,82.

В
приведенном примере рассмотрена реакция,
протекающая с
уменьшением числа молей (∆n
< 0). Полученная расчетная формула
(2.11) наглядно иллюстрирует зависимость
равновесной степени превращения от
давления в системе – повышение общего
давления ведет за собой увеличение
х_A,е.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Химическое равновесие

Количественно состояние химического равновесия характеризуется константой равновесия. Для обратимой реакции уравнения скорости прямой и обратной реакции будет выглядеть следующим образом:

$mathrm{mA + nB rightleftarrows pC + qD}$

$mathrm {v_1 = k_1[A]^m[B]^n}$ — скорость прямой реакции

$mathrm {v_2 = k_2[С]^p[D]^q}$ — скорость обратной реакции

Когда достигается равновесие, то скорости обратной и прямой реакции равны. $mathrm {k_1[A]^m[B]^n = k_2[С]^p[D]^q}$

$mathrm {K = frac {k_1}{k_2} = frac {[C]^p[D]^q}{[A]^m[B]^n}}$ — данное уравнение является математическим выражением закона действующих масс при химическом равновесии.

По численному значению константы равновесия оценивается положение равновесия. При $mathrm {K gg 1}$ равновесие смещено в сторону продуктов реакции, следовательно реакция практически необратима. При $mathrm {K ll 1}$ химическое равновесие смещается в сторону реагентов и реакция практически не идет, так как выход продуктов очень мал.

Принцип Ле Шателье

С помощью данного принципа определяются изменения, которые происходят в системе в результате внешних воздействий.

То есть внешнее воздействие меняет отношение скоростей прямого и обратного процессов, при этом благоприятствует тому процессу, который оказывает противодействие внешнему влиянию.

«Зависимость констант равновесия от температуры » 👇

Зависимость химического равновесия от температуры

Рассмотрим примеры изменения температуры в ходе определенных реакций:

• $mathrm {CO_2 + C_(т) rightleftarrows 2CO — Q}$

  Прямая реакция идет с поглощением тепла, следовательно, нагревание способствует прямой реакции, поэтому равновесие сместится в сторону продуктов реакции (в сторону экзотермической реакции).

• $mathrm {CO + H_2O_(г) rightleftarrows CO_2 + H_2 + Q}$

  Прямая реакция идет с отдачей тепла, поэтому при нагревании равновесие сместится в сторону исходных веществ (в сторону эндотермической реакции).

Правило Вант-Гоффа

Температурный коэффициент $mathrm {gamma}$ показывает, во сколько раз меняется скорость реакции при изменении температуры от $mathrm {T_1 до T_2}$.

Зная температурный коэффициент можно рассчитать изменение скорости реакции при изменении температуры:

$mathrm {frac {v(T_2)}{v(T_1} = gamma^{(T_2 — T_1)/10}}$