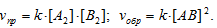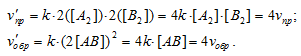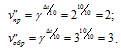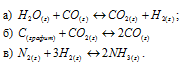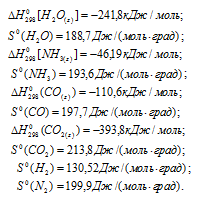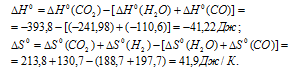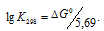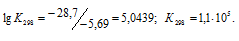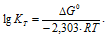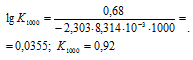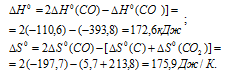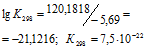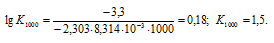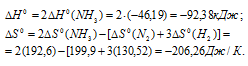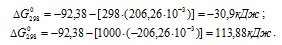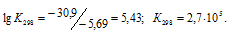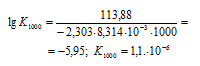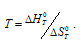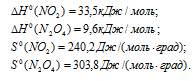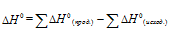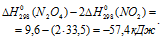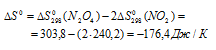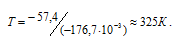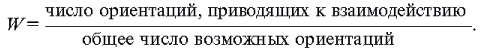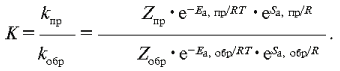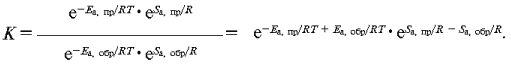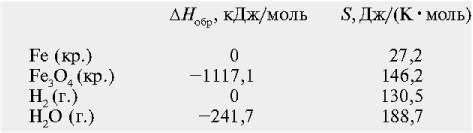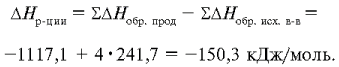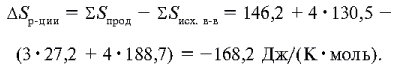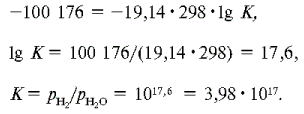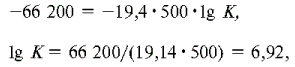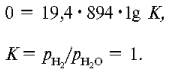Как найти константу реакции при температуре

Зависимость константы равновесия от температуры

Зависимость константы
равновесия реакции от температуры может
быть описана уравнением изобары
химической реакции (изобары Вант-Гоффа):

и изохоры химической
реакции (изохоры Вант-Гоффа):

Здесь ΔH и ΔU — тепловой
эффект реакции,
протекающей, соответственно, при
постоянном давлении или при постоянном
объёме. Если ΔH >
0 (тепловой
эффект положителен, реакция эндотермическая),
то температурный коэффициент константы

равновесия тоже
положителен, то есть с ростом температуры
константа равновесия эндотермической
реакции увеличивается, равновесие
сдвигается вправо (что вполне согласуется
с принципом
Ле Шателье).

Константа равновесия и константа скорости реакции

Для обратимой
химической реакции константа равновесия
может быть выражена через константы
скорости прямых
и обратных реакций, исходя из того факта,
что в состоянии равновесия скорости
прямой и обратной реакций равны. Например,
для элементарной обратимой химической
реакции первого порядка

легко показать, что:

где k₁ —
константа скорости прямой реакции,
а k₂ —
обратной. Это важное соотношение даёт
одну из «точек соприкосновения»
химической кинетики и химической
термодинамики.

Методы расчета константы равновесия

Расчётные методы
определения константы равновесия
реакции обычно сводятся к вычислению
тем или иным способом стандартного
изменения энергии Гиббса в ходе реакции
(ΔG⁰),
а затем использованию формулы:

При этом следует
помнить, что энергия Гиббса — функция
состояния системы,
то есть она не зависит от пути процесса,
от механизма реакции, а определяется
лишь начальным и конечным состояниями
системы. Следовательно, если непосредственное
определение или расчёт ΔG⁰ для
некоторой реакции по каким-либо причинам
затруднены, можно подобрать такие
промежуточные реакции, для
которых ΔG⁰ известно
или может быть легко определено, и
суммирование которых даст рассматриваемую
реакцию (см. Закон
Гесса).
В частности, в качестве таких промежуточных
реакций часто используют реакции
образования соединений из элементов.

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции

Энтропийный метод
расчёта ΔG реакции
является одним из самых распространённых
и удобных^[2].
Он основан на соотношении:

или, соответственно,
для стандартного изменения
энергии Гиббса:

Здесь ΔH⁰ при
постоянных давлении и температуре равно
тепловому эффекту реакции, методы
расчёта и экспериментального определения
которого известны — см., например, уравнение
Кирхгофа:

Необходимо получить
изменение энтропии в ходе реакции. Эта
задача может быть решена несколькими
способами, например:

По термическим
данным — с опорой на тепловую
теорему Нернста и
с использованием сведений о температурной
зависимости теплоёмкости участников
реакции. Например, для веществ, при
нормальных условиях находящихся в
твёрдом состоянии:

где S₀ =
0 (постулат Планка) и тогда, соответственно,

.

(здесь индекс sol —
от англ. solid). При некоторой заданной
температуре T:

Для жидких или
газообразных при нормальной температуре
веществ, или, в более общем случае, для
веществ, в интервале температур от 0
(или 298) и до T претерпевающих фазовый
переход,
следует учитывать изменение энтропии,
связанное с этим фазовым переходом.

Для идеальных газов —
методами квантовой
статистики.

Различными эмпирическими
и полуэмпирическими методами, для этого
часто достаточно небольшого объёма
исходных данных. Например, для твёрдых
неорганических веществ оценить энтропию
можно по формуле

где A и B — табличные
константы, зависящие от типа рассматриваемого
соединения, M — молекулярная масса.

Итак, если извеcтны , и
температурные зависимости
теплоёмкости, может
быть рассчитано по формуле:

Несколько упрощённый
вариант этой формулы получают, считая
сумму теплоёмкостей веществ не зависящей
от температуры и равной сумме теплоёмкостей
при 298 K:

И еще более упрощённый
расчёт проводят, приравнивая сумму
теплоёмкостей к нулю:

Переход от к
константе равновесия осуществляется
по приведённой выше формуле.

Принцип Ле Шателье —
Брауна (1884 г.) —
если на систему, находящуюся в устойчивом
равновесии, воздействовать извне,
изменяя какое-либо из условий равновесия
(температура, давление, концентрация),
то в системе усиливаются процессы,
направленные на компенсацию внешнего
воздействия.

Анри
Ле Шателье (Франция)
сформулировал этот термодинамический
принцип подвижного равновесия, позже
обобщённый Карлом
Брауном

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  27.03.2015104.12 Кб44WW.doc

Как вычислить константу равновесия реакции

Задача 366. 
В каком направлении сместится равновесие реакции  А_2(г) + В_2(г) ⇔ 2АВ_(г), если давление увеличить в 2 раза и одновременно повысить температуру на 10 градусов? Температурные коэффициенты скорости прямой и обратной реакций равны соответствен-но 2 и 3. Каков знак 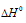  этой реакции? 
Решение:
Поскольку реакция  А_2(г) + В_2(г) ⇔ 2АВ_(г) является простой гомогенной, то для неё можно записать выражение Закона Действия Масс (ЗДМ) прямой и обратной реакций:

После увеличения давления в системе в 2 раза, соответственно, в 2 раза увеличится концентрация всех реагентов системы, имеем:

Таким образом, при увеличении давления в системе v_пр = v_обр, значит, равновесие не сместится.

Подставив данные задачи в выражение правила Вант-Гоффа, получим:

Таким образом,  v_пр < v_обр, значит, равновесие системы сместится влево, в сторону реакции с меньшей скоростью.

Повышение температуры в системе, согласно правилу Ле Шателье, приводит к смещению равновесия системы в направлении реакции, сопровождающейся поглощением теплоты, т.е. влево, значит прямая реакция экзотермическая, 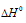  < 0.

Ответ: влево, 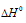  < 0.

---

Задача 367.
Пользуясь табличными данными, вычислить константы равновесия следующих реакций при 298 и при 1000 К:

Изменениями 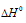 и  с температурой пренебречь.
Решение:
По табличным данным стандартные значения  веществ, участвующих в реакции равны:    

Стандартные значения 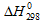 простых веществ равны нулю.

а) Находим стандартное значение 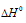 и  реакции  Н₂О_(г) + СО_(г) ⇔ СО_2(г) + Н_2(г):

Находим значение энергии Гиббса реакции из уравнения = — T, получим:

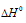
Рассчитаем константу равновесия реакции при температуре 298 K, используя формулу:

Тогда

Константу равновесия реакции при температуре 1000 К, рассчитаем по формуле:

Тогда

б) Находим стандартное значение 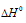 и  реакции  C_{(графит)} + СО_2(г) ⇔ 2СО_(г):

Находим значение энергии Гиббса реакции при температурах 298 К и 1000 К из уравнения   = — T , получим: 

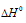
Рассчитаем константу равновесия реакции при температуре 298 К, используя формулу:

Тогда

Константу равновесия реакции при температуре 1000 К, рассчитаем по формуле:

Тогда

в) Находим стандартное значение 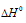 и  реакции  N_2(г) + 3H_2(г) ⇔ 2NH_3(г):

Находим значение энергии Гиббса реакции при температурах 298 К и 1000 К из уравнения   = — T , получим: 

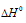
Рассчитаем константу равновесия реакции при температуре 298 К, используя формулу:

Тогда 

Константу равновесия реакции при температуре 1000 К, рассчитаем по формуле:

Тогда

Ответ: а) 1,1 ^. 10⁵, 0,92; б) 7,5 ^. 10^-22, 1,5; в) 2,7 ^. 10⁵, 1,1 ^. 10^-6.

---

Задача 368.
Вычислить температуру, при которой константа равновесия реакции 2NO_2(г) ⇔ N₂O_4(г)  равна единице. Изменениями 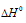 и с температурой пренебречь. В каком направлении сместится равновесие при температуре более низкой, чем найденная?
Решение:
Уравнение реакции имеет вид:  2NO_2(г) ⇔ N₂O_4(г).
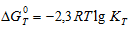
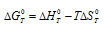
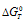
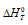
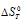
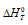
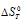
Из уравнения  следует, что при K_T = — 1 стандартная энергия Гиббса химической реакции равна нулю. Тогда из соотношения  вытекает, что при   = 0, получим: 0 =  — T  или   = T, откуда 

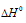
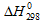
Согласно условию задачи можно пренебречь зависимостью  и  от температуры и для расчётов использовать стандартные значения энтальпии и энтропии. Стандартные значения  и ₂₉₈  реагирующих веществ равны: 

Находим 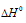  реакции, используя следствие из закона Гесса: 

Тогда

Теперь рассчитаем  реакции:

Отсюда

Ответ: 325 К.

---

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Понятие химического равновесия

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Признаки химического равновесия

1. Состояние системы остается неизменным во времени при сохранении внешних условий.
2. Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
3. Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
4. К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
5. В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Принцип Ле Шателье

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия): 

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO_(г) + O_2(г) → 2NO_2(г); ΔH^о₂₉₈ = — 113,4 кДж/моль.

Влияние температуры на химическое равновесие

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Влияние давления на химическое равновесие

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO₂. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Влияние концентрации на химическое равновесие

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O₂ вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO₂. Увеличение концентрации NO₂ смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Константа химического равновесия

Для химической реакции:

2NO_(г) + O_2(г) → 2NO_2(г)

константа химической реакции К_с есть отношение:

             К_с = [NO₂]²/([NO]² · [O₂])               (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔG_T^о = – RTlnK                      (2)

Примеры решения задач

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO _(г) + O_{2 (г)}→2CO_{2 (г)} составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение.

2CO_(г) + O_2(г) →2CO_2(г)

Вещество	CO	O2	CO2
Сисходн, моль/л	0,36	0,40	0
Спрореагир,моль/л	0,16	0,08	0,16
Сравн, моль/л	0,2	0,32	0,16

Во второй строке под С_{прореагир} понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO₂, причем, С_исходн= С_{прореагир} + С_равн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H_{2 (г)} + N_{2 (г)} →2 NH_{3 (г)} при 298 К.

Решение.

ΔG₂₉₈^о = 2·(- 16,71) кДж = -33,42·10³ Дж.

ΔG_T^о = — RTlnK.

lnK = 33,42·10³/(8,314× 298) = 13,489. K = 7,21× 10⁵.

Задача 3. Определите равновесную концентрацию HI в системе

H_2(г) + I_2(г)  →2HI_(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂ , I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H_2.

Вещество	H2	I2	HI
сисходн., моль/л	1	2	0
спрореагир., моль/л	x	x	2x
cравн., моль/л	1-x	2-x	2x

Тогда,  К = (2х)²/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H_2(г) + HCOH_(г) →CH₃OH_(г) становится равной 1. Принять, что ΔН^о_Т » ΔН^о₂₉₈, а ΔS^о_T » ΔS^о₂₉₈.

Решение.

Если К = 1, то ΔG^о_T = — RTlnK = 0;

ΔG^о_T = ΔН^о₂₉₈ — ТΔ S^о₂₉₈ .

ΔН^о₂₉₈ = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10³ Дж;

ΔS^о₂₉₈ = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52) 

Т = 786,15К

Задача 5. Для реакции SO_2(Г) + Cl_2(Г)  →SO₂Cl_2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO₂Cl₂, если исходные концентрации SO₂, Cl₂ и SO₂Cl₂ равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO_2.

SO_2(г) + Cl_2(г) →SO₂Cl_2(г)

Вещество	SO2	Cl2	SO2Cl2
cисходн., моль/л	2	2	1
cпрореагир., моль/л	x	x	х
cравн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)² = 4

Решая это уравнение, находим: x₁ = 3 и x₂ = 1,25. Но x₁ = 3 не удовлетворяет условию задачи.

Следовательно, [SO₂Cl₂] = 1,25 + 1 = 2,25 моль/л.

Задачи для самостоятельного решения

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH_{3 (г)} → 3H_{2 (г)} + N_{2 (г)}

2) ZnCO_{3 (к)} → ZnO_(к) + CO_{2 (г)}

3) 2HBr _(г) → H_{2 (г)} + Br_{2 (ж)}

4) CO_2 (г) + C _{(графит)}  →2CO _(г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr _(г)  →H_{2 (г)} + Br_{2 (г)}

составляли: [HBr] = 0,3 моль/л, [H₂] = 0,6 моль/л, [Br₂] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H_2(г) + S_(г)  →H₂S_(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H₂ и S, если исходные концентрации H₂, S и H₂S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO_2(г) + C_{(графит)}  →2CO_(г)

становится равной 1. Примите, что ΔН^о_Т≈ΔН^о₂₉₈, а ΔS^о_T≈ΔS^о₂₉₈

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С₂Н_4(г)  →С₂Н_2(г) + Н_2(г) при 298 К

6. Для реакции 2С₃Н_8(г) → н-С₅Н_12(г)+СН_4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО_2(г) + 3Н_2(г)  → СН₃ОН_(г) + Н₂О_(г)

равна 3,4·10^-5. Вычислите Δ G^о₅₀₀.

8. При температуре 800 К константа равновесия процесса н-С₆Н_14(г)+  2С₃Н_6(г)+Н_2(г) равна 8,71. Определите ΔG^о_f,800(С₃Н_6(г)), если ΔG^о_f,800(н-С₆Н_14(г)) = 305,77 кДж/моль.

9. Для реакции СО_(г) + Cl_2(г)  →СO₂Cl_2(г) при некоторой температуре равновесная концентрация СO₂Cl_2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО_(г) и Cl_2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО_2(г) + О_2(г)  →2SO_3(г) составляли: [SО₂ ]=0,10 моль/л, [О₂]=0,16 моль/л, [SО₃]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО₂ и О₂.

К=4,0; исходная концентрация SО2 составляет 0,18 моль/л; исходная концентрация О2 составляет 0,20 моль/л.

Учебная книга по химии

ДЛЯ УЧИТЕЛЕЙ СРЕДНИХ ШКОЛ, СТУДЕНТОВ
ПЕДАГОГИЧЕСКИХ ВУЗОВ И ШКОЛЬНИКОВ 9–10 КЛАССОВ,
РЕШИВШИХ ПОСВЯТИТЬ СЕБЯ ХИМИИ И ЕСТЕСТВОЗНАНИЮ

УЧЕБНИК ·
ЗАДАЧНИК · ЛАБОРАТОРНЫЙ
ПРАКТИКУМ ·НАУЧНЫЕ
РАССКАЗЫ ДЛЯ ЧТЕНИЯ

§ 3.2. Константа равновесия
и изобарный потенциал реакции

Константа равновесия легко может быть найдена
из значения изобарного потенциала, который
вычисляется по табличным данным об энтальпии
образования и энтропии исходных веществ и
продуктов реакции

Вам эта формула понадобится, когда нужно будет
вычислить константу равновесия изучаемой
реакции.

В этом учебнике мы стараемся не давать готовых
формул, а выводить их простейшими методами
математической логики, поэтому ниже приводится
вывод этой формулы. Прочитав этот материал, вы
познакомитесь с простейшими представлениями
теории вероятности, с энтропией активации и др.

Не только энергия активации определяет
скорость химической реакции. Огромную роль
играют размеры и форма реагирующих молекул и
расположение в них реакционноспособных атомов
или их групп. В связи с этим при столкновении двух
частиц важна их определенная ориентация, т. е.
контакт именно тех центров, которые являются
реакционноспособными.

Обозначим вероятность необходимой для
взаимодействия ориентации молекул при
столкновении W:

Натуральный логарифм величины W, умноженный на
газовую постоянную R, называется энтропией
активации S_a:

Из этого выражения следует:

Откуда по определению логарифма получаем
вероятность необходимой ориентации:

Чем больше вероятность необходимой ориентации
для прохождения реакции, тем выше ее скорость и
соответственно константа скорости, что можно
записать:

Раньше мы узнали, что константа скорости
зависит от энергии активации и температуры:

Таким образом, константа скорости зависит от
энергии активации, температуры и энтропии
активации:

Введем коэффициент пропорциональности Z и
поставим знак равенства:

Полученное выражение называется основным
уравнением химической кинетики.

Это уравнение объясняет некоторые стороны
катализа: катализатор понижает энергию
активации реакции и повышает энтропию активации,
т. е. повышает вероятность надлежащей для
взаимодействия ориентации реагирующих частиц.

Интересно отметить, что энтропия активации
учитывает не только определенную ориентацию
частиц, но и продолжительность контакта в момент
столкновения. Если продолжительность контакта
частиц очень мала, то их электронные плотности не
успевают перераспределиться для образования
новых химических связей, и частицы, отталкиваясь,
расходятся в разные стороны. Катализатор также в
значительной мере увеличивает
продолжительность контакта реагирующих частиц.

Еще одна особенность каталитического действия:
катализатор забирает избыток энергии с вновь
образовавшейся частицы, и она не распадается на
исходные частицы из-за своей высокой
энергетической активности.

Вы знаете, что константа равновесия – это
отношение констант скоростей прямой и обратной
реакций:

Заменим константы скоростей прямой и обратной
реакций на выражения основного уравнения
химической кинетики:

Отношение двух коэффициентов
пропорциональности Z_пр/Z_обр –
величина постоянная, которую внесем в значение
константы равновесия, отчего она останется, как и
прежде, константой.

Если вы вспомните правила действий с
показательными функциями, вам будет понятно
преобразование формулы:

В соответствии с законом Гесса разность
энергий активации обратной и прямой реакций есть
изменение энтальпии (убедитесь в этом, нарисовав
энтальпийную диаграмму реакции, проходящей с
выделением теплоты, и не забыв, что в данном
случае DН < 0):

Точно так же разность обозначим DS:

Объяснить, почему перед скобками поставлен
знак минус.

Получаем уравнение:

Прологарифмируем обе части этого уравнения:

или

Откуда имеем:

Это уравнение настолько важно для химии и
других естественных наук, что многие зарубежные
студенты-химики носят рубашки с изображением
этой формулы.

Если DG выражается в
Дж/моль, то формула приобретает вид:

У этой формулы есть одна особенность: если
константу равновесия определяют через давления
газообразных веществ, то в выражение константы
равновесия подставляют давления этих веществ в
атмосферах (1атм=101325Па=760мм рт.ст.).

Эта формула позволяет по известному значению DG реакции вычислить константу
равновесия и таким образом узнать состав
равновесной системы при заданной температуре.
Формула показывает, что чем выше константа
равновесия и чем больше в равновесной
реакционной смеси содержится продуктов реакции
(веществ, стоящих в правой части уравнения
реакции), тем более отрицательное значение имеет
изменение изобарного потенциала реакции. И
наоборот, чем ниже значение константы равновесия
и чем меньше в равновесной смеси содержится
продуктов реакции и больше исходных веществ, тем
меньше отрицательное значение DG.

Когда константа равновесия больше 1 и изобарный
потенциал отрицателен, принято говорить, что
равновесие смещено в сторону продуктов реакции,
или вправо. Когда константа равновесия меньше 1 и
изобарный потенциал положителен, принято
говорить, что равновесие смещено в сторону
исходных веществ, или влево.

При равенстве константы равновесия 1 изобарный
потенциал равен 0. Такое состояние системы
принято считать границей между смещением
равновесия вправо или влево. Когда для данной
реакции изменение изобарного потенциала
отрицательно (DG<0),
принято говорить, что реакция может проходить в
прямом направлении; если DG>0,
говорят, что реакция не проходит.

Таким образом,

DG<0 – реакция может
проходить (термодинамически возможна);

DG<0, то К>1 –
равновесие смещено в сторону продуктов, вправо;

DG>0, то К<1 –
равновесие смещено в сторону исходных веществ,
влево.

Если вам понадобится узнать, возможна ли
интересующая вас реакция (например, узнать,
возможен ли синтез нужного красителя, будет ли
спекаться данный минеральный состав, влияние
кислорода воздуха на окраску и т. п.), достаточно
рассчитать для этой реакции DG.
Если окажется, что изменение изобарного
потенциала отрицательно, то реакция возможна, и
вы можете смешивать различные исходные вещества
для получения желаемого продукта.

Прочитайте, что нужно сделать, чтобы рассчитать
изменение изобарного потенциала и константу
равновесия при различных температурах (алгоритм
расчета).

1. Выпишите из справочных таблиц значения (для
температуры 298 К) энтальпий образования из
простых веществ DН_обр
и энтропии S всех веществ, записанных в
уравнении химической реакции. Если DН_обр выражены в кДж/моль,
то их следует перевести в Дж/моль (почему?).

2. Подсчитайте изменение энтальпии в реакции (298
К) как разность между суммой энтальпий
образования продуктов и суммой энтальпий
образования исходных веществ, помня о
стехиометрических коэффициентах:

3. Подсчитайте изменение энтропии в реакции (298
К) как разность между суммой энтропий продуктов и
суммой энтропий исходных веществ, помня о
стехиометрических коэффициентах:

4. Составьте уравнение зависимости изменения
изобарного потенциала от изменений энтальпии
реакции, энтропии и температуры, подставив в
известное вам уравнение полученные только что
численные значения DН_р-ции
и DS_р-ции:

5. Подсчитайте изменение изобарного потенциала
при стандартной температуре 298 К:

6. По знаку DG_р-ции, ₂₉₈
сделайте вывод о возможности прохождения
реакции при стандартной температуре: если знак
«минус», то реакция термодинамически возможна;
если знак «плюс», то реакция невозможна.

7. Подсчитайте DG_р-ции
при интересующей вас температуре Т:

и сделайте вывод, как влияет изменение
температуры на возможность прохождения реакции.
Если окажется, что при этой температуре
изменение изобарного потенциала стало менее
положительное или более отрицательное по
сравнению с DG₂₉₈, то,
следовательно, при этой температуре реакция
становится более вероятной.

8. Вычислите из известного вам уравнения
константу равновесия K при интересующей вас
температуре Т:

9. Сделайте вывод о смещении равновесия в
сторону исходных веществ (К<1) или в сторону
продуктов (К>1).

Для заключения о возможности прохождения
реакции при отрицательном значении изменения
изобарного потенциала (DG_р-ции<0)
одних термодинамических данных часто
оказывается недостаточно. Термодинамически
возможная реакция может оказаться кинетически
заторможенной и осуществимой при изменении
условий (концентрации веществ, давление,
температура), через другие реакционные пути или в
присутствии правильно подобранного
катализатора.

Рассмотрим на примере реакции
кристаллического железа с газообразной водой
(пары воды):

как узнать о термодинамической возможности
реакции.

Эта реакция интересна тем, что показывает
причины уменьшения блеска металлического
изделия и разрушения его от коррозии.

Прежде всего подберем стехиометрические
коэффициенты уравнения реакции:

Выпишем из справочных таблиц
термодинамические данные (температура 298 К) для
всех участников реакции:

Рассчитаем изменение энтальпии в этой реакции,
вспомнив, что энтальпии простых веществ равны
нулю:

Выразим изменение энтальпии в Дж:

Реакция сопровождается выделением теплоты,
Q>0, Q=+50 300 Дж/моль, и это дает возможность
предположить, что она проходит самопроизвольно.
Однако уверенно сказать, что реакция
самопроизвольна, можно только по знаку изменения
изобарного потенциала.

Рассчитаем изменение энтропии в этой реакции,
не забыв про стехиометрические коэффициенты:

Энтропия системы в результате реакции
понижается, поэтому можно отметить, что в системе
происходит повышение порядка.

Теперь составим уравнение зависимости
изменения изобарного потенциала от изменений
энтальпии, энтропии и температуры:

Рассчитаем изменение изобарного потенциала в
реакции при стандартной температуре 298 К:

Высокое отрицательное значение изменения
изобарного потенциала говорит о том, что при
комнатной температуре железо может быть
окислено кислородом. Если бы вы смогли получить
тончайший порошок железа, то увидели бы, как
железо на воздухе сгорает. Почему на воздухе не
горят железные изделия, статуэтки, гвозди и т. п.?
Результаты расчета показывают, что на воздухе
железо корродирует, т. е. разрушается,
превращаясь в оксиды железа.

Теперь посмотрим, как влияет повышение
температуры на возможность прохождения этой
реакции. Рассчитаем изменение изобарного
потенциала при температуре 500 К:

Получили результат, показывающий, что при
повышении температуры изменение изобарного
потенциала реакции становится менее
отрицательной величиной. Это означает, что с
повышением температуры реакция становится менее
термодинамически вероятной, т. е. равновесие
реакции все сильнее смещается в сторону исходных
веществ.

Интересно узнать, при какой температуре
равновесие в одинаковой мере смещено и в сторону
продуктов реакции, и в сторону исходных веществ.
Это происходит при DG_р-ции=0
(константа равновесия равна 1):

Откуда получаем:

Т=150300/168,2=894К, или 621°С.

При этой температуре равновероятно
прохождение реакции как в прямом, так и в
обратном направлении. При температуре выше 621°С
начинает преобладать обратная реакция
восстановления Fe₃O₄ водородом. Эта
реакция является одним из способов получения
чистого железа (в металлургии оксиды железа
восстанавливают углеродом).

Рассчитать константу равновесия при
интересующей нас температуре можно по формуле

При температуре 298 К:

При 500 К:

При 894 К:

Таким образом, при повышении температуры
константа равновесия понижается.

Оксид железа Fe₃O₄ называется
магнетитом (магнитный железняк). Этот оксид
железа в отличие от оксидов FeО (вюстит) и Fe₂О₃
(гематит), притягивается магнитом. Существует
легенда, что в древности пастух по имени Магнус
нашел очень маленький продолговатый камушек,
который он своими жирными (почему это важно?)
руками положил на поверхность воды в миске.
Камушек не утонул и стал плавать по воде, причем,
как ни поворачивал миску пастух, камушек всегда
указывал только в одну сторону. Будто бы так был
изобретен компас, а минерал получил название от
имени этого пастуха. Хотя, возможно, магнетит был
так назван по имени древнего города Малой Азии –
Магнесии. Магнетит – главная руда, из которой
добывают железо.

Иногда формулу магнетита изображают так: FeО•Fe₂O₃,
подразумевая, что магнетит состоит из двух
оксидов железа. Это неправильно: магнетит –
индивидуальное вещество.

Другой оксид Fe₂О₃ (гематит) –
красный железняк – так назван из-за своего
красного цвета (в пер. с греч. – кровь). Из
гематита получают железо.

Оксид FeО почти не встречается в природе и не
имеет промышленного значения.

Список новых и забытых понятий и слов