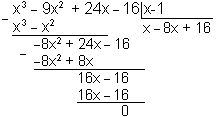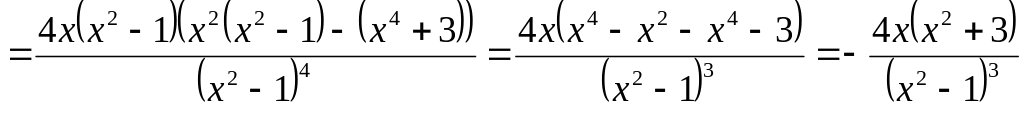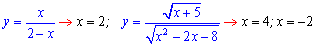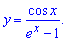Произвольно выбираем несколько значений
и находим значения функции —
Контрольные точки (x,
помогают
более точно построить график функции.
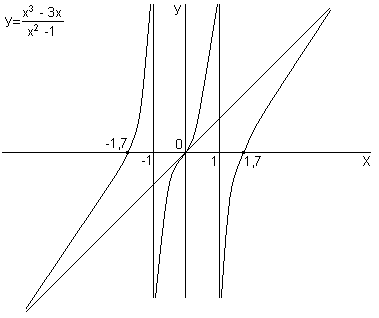
9 Построение графика функции
Построим графики функций
,
используя результаты исследования в
п.1-7
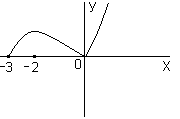
Рис.6
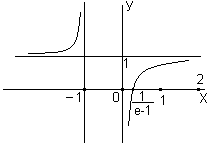
Рис.7
Замечание После того как рассмотрите построение графиков сопоставьте с результатами исследования.
10 Образцы выполнения исследования функции и построения графиков
Исследовать
поведение функции и построить график.
10.1
1 Область определения
Данная функция, существует при любом
действительном значении х, тогда
.
2 Исследование функции на четность и
нечетность
Так как область определения функции
множество четное относительно начала
координат, то найдем
:
.
Видим, что
и
,
значит функция ни четная ни нечетная,
т.е. функция общего вида.
3 Точки пересечения графика функции с
осями координат
С осью
:
полагаем
и, подставляя это значение в данную
функцию
,
находим
.
Получим точку
.
С осью
:
полагаем
,
находим
из уравнения
(*)
Корни уравнения являются делителями
свободного члена 16. Следовательно,
попробуем подставить в уравнение (*)
числа:
При
:
получаем
,
следовательно
является корнем уравнения (*). Тогда
многочлен
делится на
без остатка. Выполним деление:
Итак,
.
Уравнение (*) принимает вид:
,
откуда
(эти значения называют нулями функции).
Таким образом, график функции пересекает
ось
в точках:
.
4 Промежутки знакопостоянства функции.
Исследование функции на концах
промежутков знакопостоянства
Промежутки знакопостоянства функции
разделяют точки разрыва и нули функции.
Для данной функции – это
.
Обратите внимание, что
кратный корень, значит в интервалах
прилегающих к этой точке функция знак
не меняет. Изобразим их на числовой
оси:
Знак функции определяется непосредственной
подстановкой любого значения
из полученных интервалов в аналитическое
выражение функции.
Если на интервале
функция
отрицательная, то ее график располагается
под осью
,
на интервалах
функция положительная, то над осью
.
Для выяснения поведения функции на
концах промежутков знакопостоянства
Найдем пределы функции при
:
;
,
таким образом, знак бесконечности
определяется знаком старшего члена
.
Это означает, что слева график функции
уходит неограниченно вниз, а справа –
неограниченно вверх.
5 Асимптоты графика функции
Т.к. функция не имеет бесконечных
разрывов, то вертикальные асимптоты
отсутствуют.
Для отыскания наклонных асимптот
,
найдем
:
,
т.к
,
то график функции наклонных асимптот
не имеет.
6 Исследование функции на монотонность.
Точки экстремума
Найдем критические точки функции.
Согласно необходимого условия экстремума:
в точках экстремума производная равна
нулю или не существует.
Найдем производную:
.
Решим уравнение
:
;
;
Производная функции обращается в нуль
в точках
и
— критические точки. Они делят область
определения на интервалы монотонности
(интервалы убывания и возрастания).
Интервалы
изобразим их на числовой оси (рис.8):
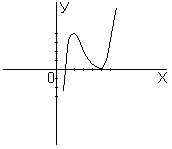
Рис.8
Поведение функции на каждом интервале
определяется знаком производной.
Для определения знака производной на
каждом интервале достаточно взять
любое значение
из этого интервала и подставить в
производную
.
На интервале
,
возьмем любое
,
например
,
и подставим в производную
.
Получили
,
следовательно функция
на интервале
возрастает.
Аналогично устанавливаем:
– на интервале
,
следовательно функция убывает;
– на интервале
,
следовательно функция возрастает.
Знаки производной
проставлены на рисунке 8 в каждом
интервале. Стрелками схематично указано
поведение функции
.
Замечаем, что при переходе через точку
производная меняет знак, с «+» на «-».
Это означает, что в точке
функция имеет максимум (на основании
достаточного условия существования
экстремума). Найдем значение
при
:
.
Значит, точка максимума
.
При переходе через точку
производная меняет знак с «-» на «+».
Это означает, что при
функция имеет минимум:
.
Точка минимума
.
7 Исследование графика функции на
выпуклость и вогнутость. Точки перегиба
Это исследование проводится с помощью
второй производной. Найдем точки,
подозрительные на перегиб, используя
необходимое условие перегиба: в точках
перегиба вторая производная либо равна
нулю, либо не существует.
Так как
,
то
и существует при любых
.
Приравняем вторую производную к нулю
и найдем корни уравнения:
.
Отсюда
– точка, подозрительная на перегиб.
Точка
делит область определения на интервалы
и
Рис.9
Определим знак второй производной на
каждом из полученных интервалов,
непосредственным способом.
На интервале
получаем
,
значит, при
график функции вогнутый (),
рисунок 8.
На интервале
получаем
,
значит, при
график функции выпуклый (),
рисунок 8.
Так как при переходе через точку
вторая производная
меняет знак, то график меняет выпуклость
на вогнутость, то есть
абсцисса точки перегиба.
.
Точка перегиба
.
8 Контрольные точки
Для более точного построения графика
найдем насколько дополнительных точек:
,
точка
9 Построение графика по полученным
результатам исследования
Замечание При исследовании
будем использовать только краткую
запись, так как все действия аналогичны
исследованной функции
.
10.2
1 Область определения
2 Исследование функции на четность и
нечетность
Так как область определения множество
симметричное относительно начала
отсчета, то найдем
:
.
Делаем вывод: функция нечетная. Для
дальнейшего исследования будем
использовать свойства нечетной функции
на симметричных интервалах:
– меняет знакопостоянство;
– сохраняет монотонность;
– точки максимума и минимума симметричны
относительно начала координат;
– меняет выпуклость на вогнутость;
– график функции симметричен относительно
начала координат.
3 Точки пересечения графика функции с
осями координат
С осью
:
.
Решим уравнение:
.
Получили точки:
С осью
:
.
. Получили
точку
.
4 Промежутки знакопостоянства функции.
Исследование функции на концах
промежутков знакопостоянства
Для выяснения поведения функции на
концах промежутков знакопостоянства
вычислим следующие пределы:
5 Асимптоты графика функции
5.1 Так как в точках
функция
претерпевает бесконечный разрыв, то
график функции имеет вертикальные
асимптоты :
5.2
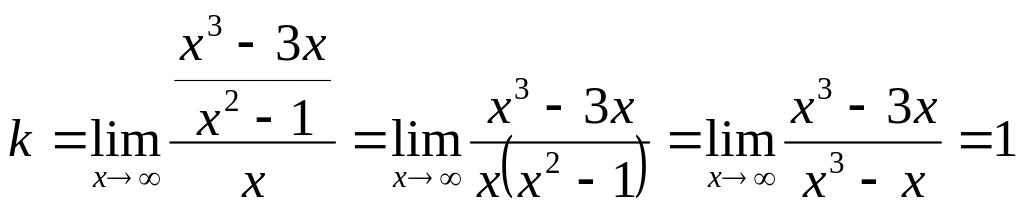
.
Получили
– наклонная асимптота.
6 Исследование функции на монотонность.
Экстремумы функции
Решим уравнение
:
Критические точки (по первой производной):
точек, в которых производная равна нулю
нет,
Отметим на числовой прямой критические
точки и исследуем знак производной на
каждом из полученных интервалов
Делаем вывод, что функция возрастает
на всей области определения.
Так как функция в области определения
монотонности не меняет, то точек
экстремума нет.
7 Исследование графика функции на
выпуклость и вогнутость. Точки перегиба
Найдем вторую производную функции:

.
Решим уравнение
:
Критические точки (по второй производной):
Отметим на числовой прямой полученные
точки и исследуем знак второй производной
При
график функции имеет перегиб.
Точка
– точка перегиба.
9 Контрольные точки
|
|
|
|
|
|
|
|
9 Построение графика по полученным
результатам исследования
При построении графика помним, что он
симметричен относительно точки
.
11.3
Замечаем, что функция задана в неявном
виде. Выразим y в явном
виде
.
Достаточно
исследовать и построить график функции
,
а за тем отобразить симметрично оси
OX.
1 Область определения функции

Решим методом интервалов:
.
Делаем вывод:
.
На интервалах
и
функция в дальнейшем не исследуется,
т.к. они не входят в область определения.
2 Исследование функции на четность и
нечетность
Так
как область определения множество
несимметричное относительно начала
координат, то делаем вывод, что функция
ни четная ни нечетная.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Критические точки – это точки в которых производная функции равна нулю или не существует. Если производная равна 0 то функция в этой точке принимает локальный минимум или максимум. На графике в таких точках функция имеет горизонтальную асимптоту, то есть касательная параллельна оси Ох.
Такие точки называют стационарными. Если видите на графике непрерывной функции «горб» или «яму» помните, что максимум или минимум достигается в критической точке. Рассмотрим для примера следующее задание.
Пример 1. Найти критические точки функции y=2x^3-3x^2+5 .
Решение. Алгоритм нахождения критических точек следующий:
Итак функция имеет две критические точки.
Далее, если нужно провести исследование функции то определяем знак производной слева и справа от критической точки. Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция принимает локальный минимум. Если с «+» на «-» должны локальный максимум.
Второй тип критических точек это нули знаменателя дробных и иррациональных функций
Функции с логарифмами и тригонометрические, которые не определены в этих точках
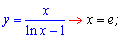
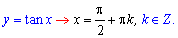
Третий тип критических точек имеют кусочно-непрерывные функции и модули.
Например любая модуль-функция имеет минимум или максимум в точке излома.
Например модуль y = | x -5 | в точке x = 5 имеет минимум (критическую точку).
Производная в ней не существует, а справа и слева принимает значение 1 и -1 соответственно.
Попробуйте определить критические точки функций
1) 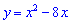
2) 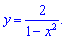
3) 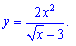
4) 
5)
Если в ответе у Вы получите значение
1) x=4;
2) x=-1;x=1;
3) x=9;
4) x=Pi*k;
5) x=1.
то Вы уже знаете как найти критические точки и сможете справиться с простой контрольной или тестами.
Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.
А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Полезная страница? Сохрани или расскажи друзьям
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
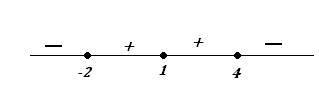
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
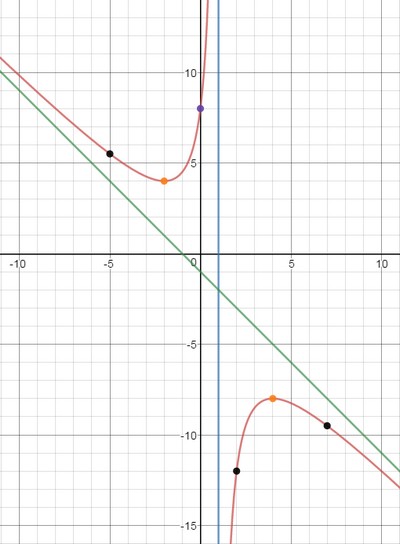
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

.
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=frac{x^3-1}{4x^2}.$$
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
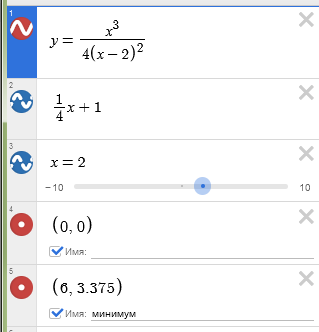
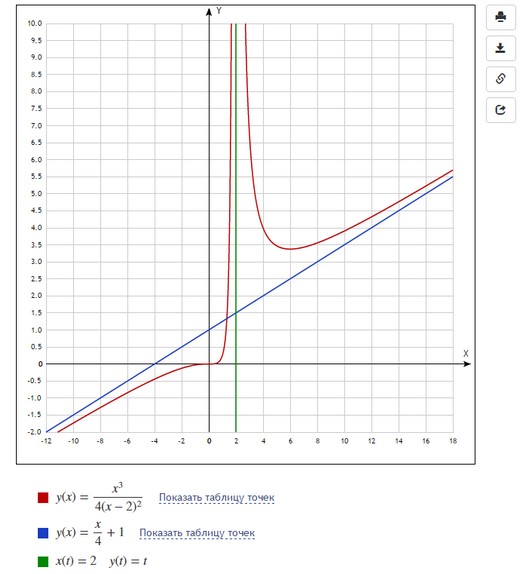
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
Сайт для построения графиков y(x).ru
y(x).ru
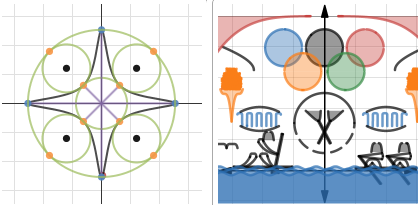
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
И такой график получается в итоге:
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Спасибо за ваши закладки и рекомендации
Как найти критические точки функции
При построении графика функции необходимо определить точки максимума и минимума, промежутки монотонности функции. Чтобы ответить на эти вопросы первым делом нужно найти критические точки, то есть такие точки области определения функции, в которых производная не существует или равна нулю.

Вам понадобится
- Умение находить производную функции.
Инструкция
Найдите область определения D(x) функции y=ƒ(x), так как все исследования функции проводятся в том интервале, где функция имеет смысл. Если вы исследуете функцию на некотором промежутке (a; b), то проверьте, чтобы этот интервал принадлежал области определения D(x) функции ƒ(x). Проверьте функцию ƒ(x) на непрерывность в этом промежутке (a; b). То есть lim(ƒ(x)) при x стремящимся к каждой точке x0 из интервала (a; b) должен быть равен ƒ(x0). Также функция ƒ(x) должна быть дифференцируема на этом интервале за исключением возможно конечного числа точек.
Вычислите первую производную ƒ'(x) функции ƒ(x). Для этого воспользуйтесь специальной таблицей производных элементарных функций и правилами дифференцирования.
Найдите область определения производной ƒ'(x). Выпишите все точки, которые не попали в область определения функции ƒ'(x). Отберите из этого множества точек только те значения, которые принадлежат области определения D(x) функции ƒ(x). Это и будут критические точки функции ƒ(x).
Отыщите все решения уравнения ƒ'(x)=0. Выберите из этих решений только те значения, которые попадают в область определения D(x) функции ƒ(x). Эти точки так же будут являться критическими точками функции ƒ(x).
Рассмотрите пример. Пусть дана функция ƒ(x)=2/3×x^3−2×x^2−1. Область определения этой функции вся числовая прямая. Найдите первую производную ƒ'(x)=(2/3×x^3−2×x^2−1)’=(2/3×x^3)’−(2×x^2)’=2×x^2−4×x. Производная ƒ'(x) определена при любом значении x. Тогда решите уравнение ƒ'(x)=0. В данном случае 2×x^2−4×x=2×x×(x−2)=0. Этому уравнению равносильна система из двух уравнений: 2×x=0, то есть x=0, и x−2=0, то есть x=2. Эти два решения принадлежат области определения функции ƒ(x). Таким образом, у функции ƒ(x)=2/3×x^3−2×x^2−1 существует две критические точки x=0 и x=2.
Обратите внимание
Знак ^ обозначает возведение в степень, знак ‘ – взятие производной.
Источники:
- критических точек функции
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
- Критические точки и экстремумы функции
- Теорема Ферма (Необходимое условие существовании экстремумов)
- Достаточное условие существования экстремума
- Задача пример №117
- Задача пример №118
- Задача пример №119
- Задача пример №120
- Задача пример №121
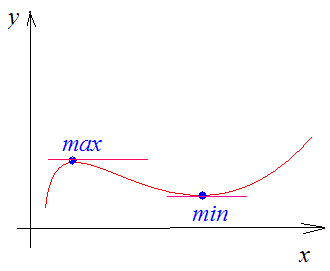
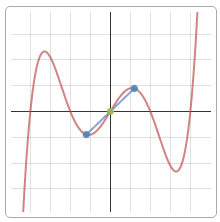
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 


2. В точках 
3. Для рассматриваемой нами функции критические точки 

По графику видно, что в точках внутреннего экстремума 

Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума
Пусть функция 



1 ) 


2) 


3) 


Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 



Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Задача пример №117
Для функции 
Решение:
Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 

Проверим знак 



Интервал 
Знак 

При 

При 

4. Используя полученные для функции 

Задача пример №118
Найдите наибольшее и наименьшее значение функции 
Решение:
Сначала найдем критические точки. Так как 



Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Задача пример №119
Найдите экстремумы функции 
Решение:
1. Производная функции:
2. Критические точки: 
3. Интервалы, на которые критические точки делят область определения функции:
Проверим знак 
Для промежутка 
Для промежутка (0; 1,5) возьмем
Для промежутка 
Интервал
Пробные точки
Знак 

Используя полученную для функции 



• Функция 

• Точка 

• Функция 
• Функция 

•
Задача пример №120
Найдите экстремумы функции
Решение:
1. Производная
2. Критические точки: для этого надо решить уравнение 



3. Промежутки, на которые критическая точка делит область определения функции: 
Определим знак 
Для 


Интервал 
Знак 
Возрастание-убывание
• Функция 

• Функция 

•
Задача пример №121
По графику функции производной 
Решение:
Производная 







Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Экстремумы функции двух переменных. Производная по направлению
- Доказательство неравенств
- Системы уравнений
- Максимальные и минимальные значения функции
- Действия с корнями
- Отрицательное биномиальное распределение
- Длина дуги кривой
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма