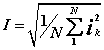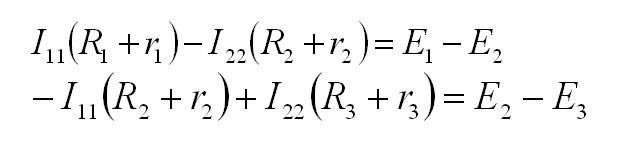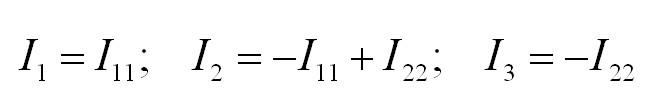Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
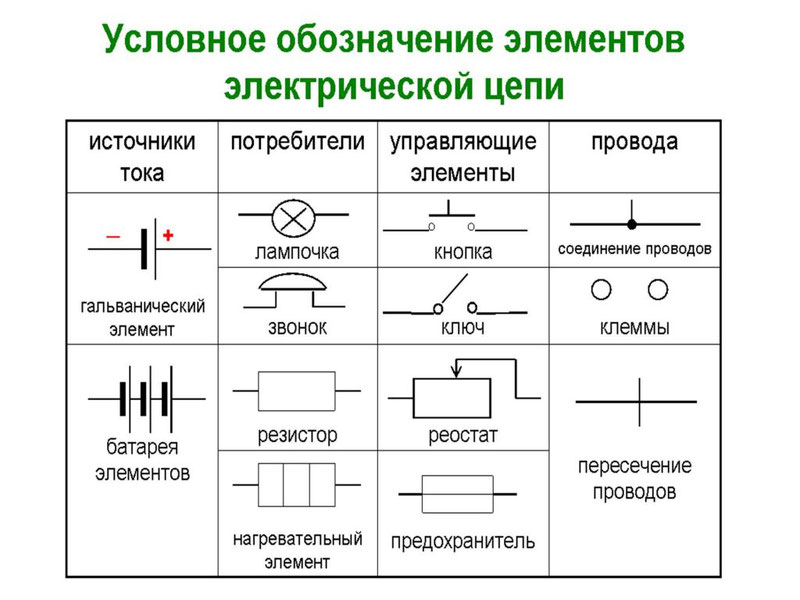
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
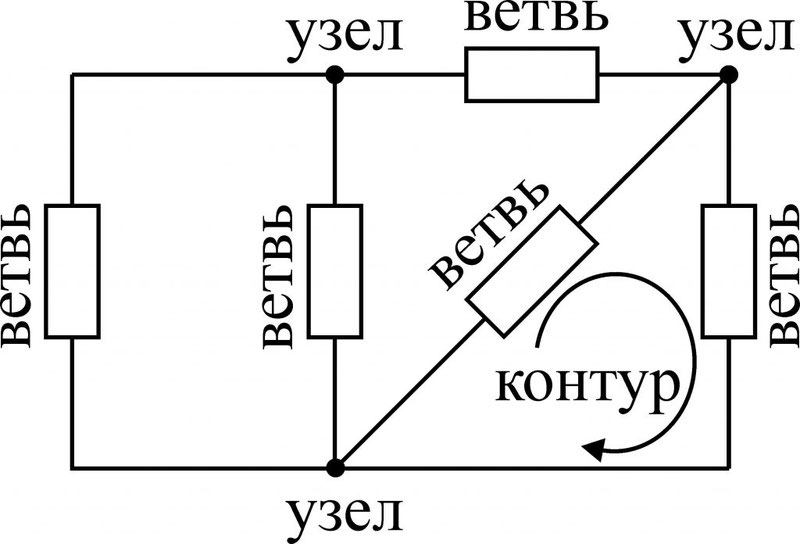
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и 
- Узел A
- Узел B
- Узел C
- Узел D
Точки К и Е не являются узлами.
Контур — это замкнутый участок электрической цепи (схемы), составленный из одной или нескольких ветвей. Любой замкнутый путь, проложенный через ветви цепи и есть замкнутый контур.
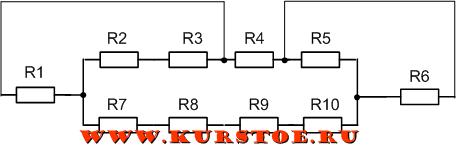
На рисунке изображен замкнутый контур из сопротивлений R2, R3, R4, R5, R7, R8, R9, R10.
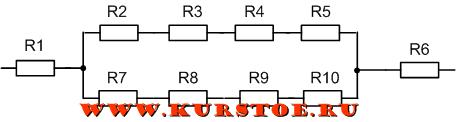
Количество контуров в схеме — 6
Это следующие контура:
R1, R2, R3
R5, R6
R1, R4, R5, R10, R9, R8, R7
R2, R3, R4, R5, R10, R9, R8, R7
R2, R3, R4, R6, R10, R9, R8, R7
R1, R4, R6, R10, R9, R8, R7
-
Узел электрической
цепи — это
точка
разветвленной электрической цепи, в
которой соединяются не менее трех
элементов друг с другом или с источником
электрической энергии; -
Ветвь электрической
цепи — это
отрезок
разветвленной электрической цепи,
заключенный между двумя ее узлами; -
Контур электрической
цепи — это
участок
разветвленной
электрической цепи, по которому может
замыкаться электрический ток от
источника электрической энергии
(замкнутый путь тока по нескольким
ветвям).
2. Элементы электрических цепей
2.1. Резисторы
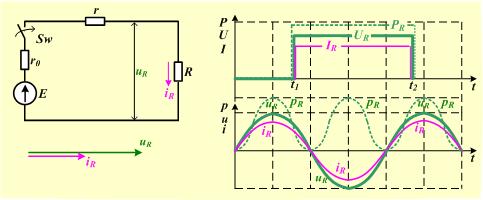
На схеме приняты
следующие обозначения:
E —
источник электродвижущей силы (ЭДС);
r0
— внутреннее сопротивление источника
ЭДС;
r —
сопротивление проводников и электронных
коммутаторов;
Sw —
коммутирующий ключ.
2.1.1. Определения
Резистор —
это диссипативный
(рассеивающий электрическую энергию в
тепло) элемент электрической цепи,
который имеет свойство оказывать
противодействие
протекающему по нему электрическому
току iR
под воздействием приложенного
электрического напряжения uR.
Электрическое
сопротивление (R)
— это количественный показатель,
характеризующий свойство резистора
оказывать противодействие протеканию
электрического тока, который в
соответствии с законом
Ома
определяется следующим образом:
R [Ом]
= uR
[В] / iR[А];
Соотношения основных
величин:
1 Ом = 10-3
кОм = 10-6
МОм = 10-9
ГОм
2.1.2. Основные
соотношения при переменном синусоидальном
напряжении (см.
нижние графики)
Внешнее напряжение,
которое будет приложено к резистору
после включения ключа Sw:
uR(t)
= Umsint
где:
= 2f
= 2
/ T
— угловая частота изменения напряжения, f
— частота изменения напряжения, T
— период изменения напряжения, uR(t)
— мгновенное
значение напряжения, Um
— амплитудное значение напряжения.
Электрический
ток в
соответствии с законом
Ома
будет иметь вид:
iR(t)
= uR(t)
/ R
= Umsint
/ R
= Imsint,
где iR(t)
— мгновенное значение тока, Im
= Um
/ R
— амплитудное
значение электрического тока.
Электрический
ток в активном сопротивлении совпадает
по фазе с приложенным к нему напряжением.
Средние значения
тока и напряжения за
полный период равны нулю
(поскольку мгновенные значения за
положительный и отрицательный полупериоды
равны и противоположны по знаку), а за
положительный полупериод (по определению):
=0.637
Im
;
Uср
= 0.637 Um
Если измерение
синусоидальных сигналов тока и напряжения
производится дискретными средствами
(Аналого-Цифровыми Преобразователями
— АЦП), то в соответствии с методом
мгновенных значений:
;
где N
— число мгновенных замеров на полупериоде
(для точного воспроизведения формы
сложного сигнала рекомендуется выбирать
N=50-100);
ik
, uk—
мгновенные значение тока и напряжения (1<k<N).
Действующие
значения тока
и напряжения (по определению):
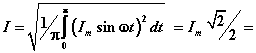
= 0,707
Im; U
= 0.707 Um
Если измерение
синусоидальных сигналов тока и напряжения
производится дискретными средствами
(Аналого-Цифровыми Преобразователями
— АЦП), то в соответствии с методом
мгновенных значений:
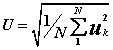
где N
— число мгновенных замеров на полупериоде
(для точного воспроизведения формы
сложного сигнала рекомендуется выбирать
N
= 50-100); ik,
uk
— мгновенные значение тока и напряжения
(1<k<N)
Мощность
электрических потерь,
рассеиваемая на резисторе (среднее
значение мгновенной мощности p(t)
за полупериод основной частоты источника
электрической энергии):
pR(t)
[Вт] = uR(t)
[В] iR(t)
[А] = Umsint
Imsint
= UmIm
(1 — cos2t)
/ 2
где UmIm
/ 2 = UI
— постоянная
составляющая активной мощности, Um,
Im
— максимальные значения напряжения и
тока, U,
I
— действующие значения напряжения и
тока, UmImcos2t
/ 2 — переменная
составляющая активной мощности, которая
изменяется с двойной
частотой источника
электрической энергии и не создает
активных потерь, поскольку среднее
значение за период от этой составляющей
равно нулю.
Если измерение
синусоидальных сигналов тока и напряжения
производится синхронизированными
(в одно и то
же мгновение) дискретными средствами
(Аналого-Цифровыми Преобразователями
— АЦП), то в соответствии с методом
мгновенных значений:
где N
— число мгновенных замеров на полупериоде
(для точного воспроизведения формы
сложного сигнала рекомендуется выбирать
N
= 50-100); ik
, uk
— синхронно замеренные мгновенные
значение тока и напряжения (1<k<N)
2.1.3. Основные
соотношения при постоянном напряжении
(см. верхние
графики)
Внешнее напряжение,
которое будет приложено к резистору
после включения ключа Sw:
u(t)
= U
= const
Электрическая
ток в
момент времени t1
после включения ключа Sw
скачком нарастет до величины:
iR(t)
= IR
= UR
/ R
= const
Активная мощность
электрических потерь PR
на резисторе R
от протекающего по нему постоянного
тока IR
выражается следующими зависимостями:
PR
= URIR
= IR2R
= UR2
/ R
= const
При отключении
постоянного напряжения в момент времени
t2
ток и мощность скачком изменяются до
нуля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Электрические цепи
Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
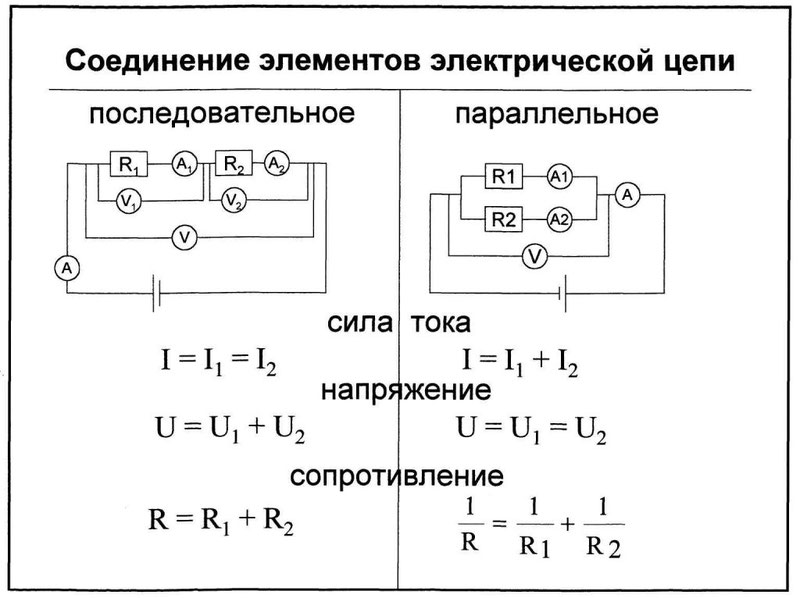
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Классификация электрических цепей
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
Расчет электрических цепей
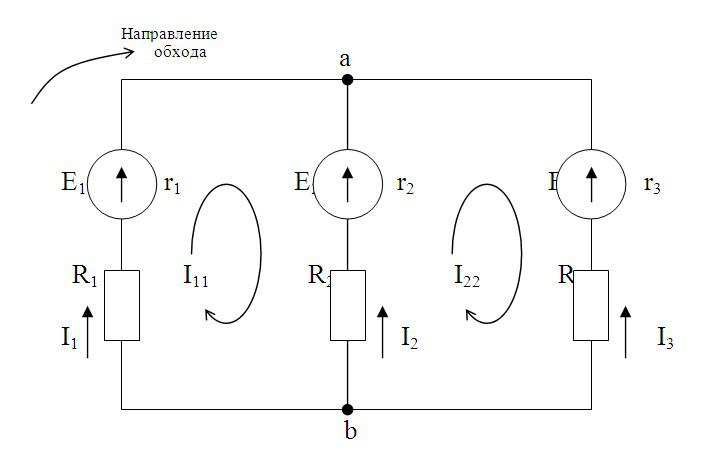
Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов
Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!
Содержание:
- Метод расчета электрической цепи с применением контурных токов
- Алгоритм расчета электрической цепи методом контурных токов
- Пример задачи с решением 1
- Пример задачи с решением 1.1.1
- Пример задачи с решением 1.1.2
Метод расчета электрической цепи с применением контурных токов
Для расчета электрической цепи методом контурных токов выбирается система независимых контуров, по которым протекают контурные токи, направление которых выбирается произвольно. Если ветвь включена только в одну цепь, ток в этой ветви равен току в цепи. Если ветвь включена в более чем одну цепь, ток в этой ветви равен сумме токов цепи, проходящих через эту ветвь, с учетом знака и выбранного направления. Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.
Алгоритм расчета электрической цепи методом контурных токов
1. Вычерчиваем принципиальную схему цепи и обозначаем все элементы, задаем направления токов ветвей.
2. Определяем все независимые контуры.
3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры 
4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи уравнений учитывайте, что направление обхода цепи, из которого создаются уравнения, совпадает с направлением тока цепи в этой цепи. Необходимо учитывать тот факт, что в соседних ветвях, принадлежащих к двум цепям, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5. Решаем любым методом полученную систему относительно контурных токов и определяем их.
6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры 
7. Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Возможно вам будут полезны данные страницы:
Пример задачи с решением 1
Определить токи в ветвях схемы рис. 4 методом контурных токов. Правильность решения проверить по балансу мощностей.

1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 4
2. Определяем независимые контура и выбираем направления контурных токов
3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток 





Хотя все токи в ветвях можно определить методом контурных токов 

для узла





Пример задачи с решением 1.1.1
Методом контурных токов определить токи в ветвях схемы (рисунок 1) если 

Определяем количество уравнений системы:
Выбираем контуры и записываем для каждого уравнения по второму закону Кирхгофа:

Затем выражаем токи ветвей из контурных токов:


Пример задачи с решением 1.1.2
Методом контурных токов определить токи в ветвях схемы (рисунок 2), если

Определяем количество уравнений системы:
Первый независимый контур выбираем так, чтобы он был образован ветвью с идеальным источником тока .7, и контурный ток данного контура считаем равным току источника тока 
Запишем систему уравнений:


Методом наложения определяем токи в ветвях схемы:



Для схемы рисунка 2 напряжение 
откуда

Тогда