Как найти контурные интегралы - Исправление недочетов и поиск решений вместе с Examum.ru

Вычисление интегралов с помощью вычетов

Вычисление контурных интегралов с помощью вычетов

Рассмотрим несколько примеров на применение вычетов к вычислению интегралов по замкнутому контуру, т.е. на применение основной теоремы о вычетах (утверждение 4.6 , формула (4.19)). Использование формулы (4.19) предполагает выполнение ряда действий, связанных с формой ее записи.

Алгоритм вычисления контурных интегралов с помощью вычетов

1. Найти особые точки функции f(z) .

2. Определить, какие из этих точек расположены в области , ограниченной контуром . Для этого достаточно сделать чертеж: изобразить контур и отметить особые точки.

3. Вычислить вычеты в тех особых точках, которые расположены в области.

4. Записать результат по формуле (4.19):

$ointlimits_{C}f(z),dz= 2pi i sum_{k=1}^{n} mathop{operatorname{res}}limits_{z=z_k}f(z),quad z_kin D.$

▼ Примеры 4.28-4.35 вычисления контурных интегралов с помощью вычетов

Пример 4.28. Вычислить контурный интеграл $ointlimits_{|z-1|=1} frac{dz}{z^4+1}$ .

Решение

Записываем решение по алгоритму.

1. Конечными особыми точками функции $f(z)= frac{1}{z^4+1}$ являются нули знаменателя, z^4+1=0 , то есть $z_k=exp left[left(frac{pi}{4}+k frac{pi}{2}right)!iright]$ . Заметим, что все точки — простые нули знаменателя, следовательно, простые полюсы f(z) .

2. Контуром интегрирования является окружность |z-1|=1 , а точки z_k расположены в вершинах квадрата, вписанного в окружность |z|=1 (рис. 4.4). Поэтому в область, ограниченную контуром, попадают точки $z_1=exp frac{ipi}{4}$ и $z_2= exp frac{i7pi}{4}= exp frac{-ipi}{4}$ .Заметим, что $z_2= overline{z}_1$ .

Рис. 4.4.

3. Находим вычеты в точках z_1 и z_2 по формуле (4.24):

$mathop{operatorname{res}}limits_{z=z_1} frac{1}{z^4+1}= frac{1}{4z_1^3}= frac{1}{4}exp frac{-i3pi}{4};qquad mathop{operatorname{res}}limits_{z=z_2} frac{1}{z^4+1}= frac{1}{4z_2^3}= frac{1}{4}exp frac{i3pi}{4},.$

Записываем ответ:

$ointlimits_{|z-1|=1} frac{dz}{z^4+1}= 2pi icdot frac{1}{4}! left(exp frac{-i3pi}{4}+ exp frac{i3pi}{4}right)= pi icosfrac{3pi}{4}= pi i! left(-frac{sqrt{2}}{2}right)=-frac{ipisqrt{2}}{2},.$

Пример 4.29. Вычислить интегралы: а) $ointlimits_{|z|=1} z^3exp frac{1}{z},dz$ ; б) $ointlimits_{|z-1|=2}sin! left(1+frac{1}{z}right)!dz$ .

Решение

Единственной конечной особой точкой каждой из подынтегральных функций является z=0 — существенно особая точка. В обоих случаях она принадлежит области, ограниченной контуром интегрирования. Вычеты находим, раскладывая функции по степеням (см. примеры 4.23, 4.24). Получаем

$mathop{operatorname{res}}limits_{z=0} z^3exp frac{1}{z}=frac{1}{24},,qquad mathop{operatorname{res}}limits_{z=0}sin! left(1+frac{1}{z}right)=cos1.$

Записываем ответ: a) $ointlimits_{|z|=1} z^3exp frac{1}{z},dz= frac{ipi}{12}$ ; б) $ointlimits_{|z-1|=2} sin! left(1+frac{1}{z}right)!dz= 2pi icos1$ .

Пример 4.30. Вычислить интегралы: a) $ointlimits_{left|z+frac{1}{2}right|=1} frac{iz(z-1)}{sinpi z},dz$ ; б) $ointlimits_{|z-i|=1} frac{z}{e^z-i},dz$ .

Решение

а) Воспользуемся алгоритмом.

1. Находим конечные особые точки функции $f(z)= frac{iz(z-1)}{sinpi z}$ — корни уравнения sinpi z=0 , то есть pi z=pi k , или $z_k=k,~ kinmathbb{Z}$ .

2. В область $left|z+frac{1}{2}right|<1$ входят точки z_1=0,~z_2=-1 . так как $left|z_1+frac{1}{2}right|=frac{1}{2}<1$ и $left|z_1+ frac{1}{2}right|= frac{1}{2}<1$ . Другие точки не принадлежат кругу $left|z+frac{1}{2}right|<1$ , так как для них $left|z_k+frac{1}{2}right|>1$ . В этом можно также убедиться, сделав чертеж.

3. Точка z=0 — устранимая особая точка функции, так как $limlimits_{zto0} frac{iz(z-1)}{sinpi z}= limlimits_{zto0}frac{iz(z-1)}{pi z}= frac{-i}{pi}$ ; поэтому $mathop{operatorname{res}}limits_{z=0}f(z)=0$ .Точка z=-1 является полюсом первого порядка f(z) , так как она — простой нуль знаменателя, а числитель при этом не обращается в нуль, т.е. функция может быть записана в виде $f(z)= frac{varphi(z)}{z+1}$ . Вычет вычисляем по формуле (4.24):

$mathop{operatorname{res}}limits_{z=-1}frac{iz(z-1)}{sinpi z}= left.{frac{iz(z-1)}{(sinpi z)'}}right|_{z=-1}= left.{ frac{iz(z-1)}{picospi z}}right|_{z=-1}= frac{2i}{picospi}= frac{-2i}{pi},.$

4. Запишем ответ: $ointlimits_{left|z+frac{1}{2}right|=1} frac{iz(z-1)}{sinpi z},dz= 2pi icdot frac{-2i}{pi}=4$ .

б) Воспользуемся алгоритмом.

1. Особыми точками функции являются нули знаменателя, т.е. корни уравнения e^z-i=0 , или $e^z= exp! left[i!left(frac{pi}{2}+2kpiright)right]$ , то есть $z_k= i!left(frac{pi}{2}+2kpiright)!,~ kinmathbb{Z}$ .

2. Из всех точек $z_k= i!left(frac{pi}{2}+2kpiright)!,~ kinmathbb{Z}$ кругу |z-i|<1 принадлежит только одна точка $z=i,frac{pi}{2}$ .

3,4. Находим вычет в точке $z=i,frac{pi}{2}$ — простом полюсе f(z)colon

$mathop{operatorname{res}}limits_{z=i,frac{pi}{2}} frac{z}{e^z-i}= left.{frac{z}{(e^z-i)'}}right|_{z=i,frac{pi}{2}}= left.{frac{z}{e^z}}right|_{z=i,frac{pi}{2}}= i,frac{pi}{2}cdot frac{1}{exp frac{ipi}{2}}= i,frac{pi}{2}cdot frac{1}{i}= frac{pi}{2},.$

Записываем ответ: $ointlimits_{|z-i|=1} frac{z}{e^z-i},dz= 2pi icdot frac{pi}{2}= pi^2i$ .

Пример 4.31. Вычислить контурные интегралы: а) $ointlimits_{|z|=2} frac{dz}{(z+3)(z^{15}-1)}$ ; б) $ointlimits_{|z-1|=1} frac{dz}{z-1}cos frac{z}{2z-1}$ .

Решение

а) Особыми точками функции являются простые полюсы z_0=-3 и $z_k=sqrt[LARGE{15}]{1}= exp frac{i2kpi}{15},,~ k=1,2,ldots,15$ . Точка z_0 не принадлежит области |z|<2 , а точки z_k расположены на окружности |z|=1 , следовательно, входят в область |z|<2 . Применяя формулу (4.19), можно найти вычеты в этих точках и получить ответ:

$ointlimits_{|z|=2} frac{dz}{(z+3)(z^{15}-1)}= 2pi icdot sum_{k=1}^{15} mathop{operatorname{res}}limits_{z=z_k} frac{1}{(z+3)(z^{15}-1)},.$

Чтобы не вычислять вычеты в 15 особых точках z_k , используем обобщенную теорему о вычетах (формулу (4.20)). В данном случае она имеет вид $sum_{k=1}^{15} mathop{operatorname{res}}limits_{z=z_k}f(z)=-left(mathop{operatorname{res}}limits_{z=-3} f(z)+ mathop{operatorname{res}}limits_{z=infty} f(z)right)$ и, следовательно,

$ointlimits_{|z|=2} frac{dz}{(z+3)(z^{15}-1)}= -2pi i!left(mathop{operatorname{res}}limits_{z=-3} f(z)+ mathop{operatorname{res}}limits_{z=infty} f(z)right)!.$

Точка z=-3 — простой полюс f(z) , и вычет находим по формуле (4.24):

$mathop{operatorname{res}}limits_{z=-3}f(z)= left.{frac{1}{z^{15}-1}}right|_{z=-3}= frac{-1}{3^{15}+1},.$

Точка z=infty — устранимая особая точка для f(z) и $limlimits_{ztoinfty} f(z)=0$ . Вычет вычисляем по формуле (4.26):

$mathop{operatorname{res}}limits_{z=infty}f(z) mathop{operatorname{res}}limits_{z=infty} frac{1}{(z+3)(z^{15}-1)}= limlimits_{ztoinfty} frac{-z}{(z+3)(z^{15}-1)}=0.$

Получаем ответ: $ointlimits_{|z|=3} frac{dz}{(z+3)(3^{15}-1)}= frac{2ipi}{3^{15}+1}$ .

б) Особыми точками функции являются z=1 — простой полюс и $z=frac{1}{2}$ — существенно особая точка. Обе точки принадлежат кругу |z-1|<1 .

Вычет в точке z=1 находим по формуле (4.24): $mathop{operatorname{res}}limits_{z=1}f(z)= left.{cos frac{z}{2z-1}}right|_{z=1}= cos1$ . Для нахождения вычета в точке $z=frac{1}{2}$ -существенно особой точке — нужно найти коэффициент $c_{-1}$ , т.е. записать разложение функции в ряд по степеням $left(z-frac{1}{2}right)$ . Для этого записываем разложения функций $f_1(z)=cosfrac{z}{2z-1}$ и $f_2(z)=frac{1}{z-1}$ , перемножаем ряды и находим $c_{-1}$ — коэффициент при степени $left(z-frac{1}{2}right)^{-1}= frac{1}{z-frac{1}{2}}$ .

Если, как и в предыдущем случае, использовать формулу (4.20), то задача вычисления интеграла упрощается, так как нет необходимости вычислять вычет в существенно особой точке $z=frac{1}{2}$ . Действительно, из

$mathop{operatorname{res}}limits_{z=frac{1}{2}}f(z)+ mathop{operatorname{res}}limits_{z=1}f(z)+ mathop{operatorname{res}}limits_{z=infty} f(z)=0$ следует $mathop{operatorname{res}}limits_{z=frac{1}{2}}f(z)+ mathop{operatorname{res}}limits_{z=1}f(z)=-mathop{operatorname{res}}limits_{z=infty} f(z)$ .

Поэтому $mathop{operatorname{res}}limits_{z=infty}f(z)= limlimits_{ztoinfty} frac{-zcos frac{z}{2z-1}}{z-1}=-cos dfrac{1}{2}$ и $ointlimits_{|z-1|=1} frac{cos dfrac{z}{2z-1}}{z-1},dz= 2pi icosfrac{1}{2}$ .

Пример 4.32. Вычислить интеграл $ointlimits_{C} frac{1}{z^2-1}sin frac{pi z}{2z+1},dz$ , где — граница круга единичного радиуса с центром в точке z_0colon a) z_0=1 ; б) z_0=-1 .

Решение

Особыми точками подынтегральной функции являются z_1=-1 — полюс первого порядка, $z_2=-frac{1}{2}$ — существенно особая точка и z_3=-1 — устранимая особая точка (см. пример 4.21).

а) В круг |z-1|<1 входит одна точка z=1 . Находим вычет по формуле (4.24):

$mathop{operatorname{res}}limits_{z=1}f(z)= left.{frac{1}{2z} sinfrac{pi z}{2z}}right|_{z=1}= frac{1}{2}sin frac{pi}{3}= frac{sqrt{3}}{4},.$

Получаем ответ: $ointlimits_{|z-1|=1} frac{1}{z^2-1}sin frac{pi z}{2z+1},dz= frac{ipi}{2}sqrt{3}$ .

б) В круг |z+1|<1 входят две точки: $z=-frac{1}{2}$ — существенно особая точка и z=-1 — устранимая особая точка. Поэтому

$ointlimits_{|z+1|=1} frac{1}{z^2-1}sin frac{pi z}{2z+1},dz= 2pi i! left(mathop{operatorname{res}}limits_{z=1}f(z)+ mathop{operatorname{res}}limits_{z=-frac{1}{2}}f(z)right)!,$

или, применяя формулу (4.20) (чтобы избежать вычисления вычета в существенно особой точке), получаем

$ointlimits_{|z+1|=1} frac{1}{z^2-1}sin frac{pi z}{2z+1},dz=-2pi i! left(mathop{operatorname{res}}limits_{z=1}f(z)+ mathop{operatorname{res}}limits_{z=infty}f(z)right)!.$

Так как $limlimits_{ztoinfty}f(z)=0$ , находим $mathop{operatorname{res}}limits_{z=infty}f(z)$ по формуле (4.24):

$mathop{operatorname{res}}limits_{z=infty}f(z)= limlimits_{ztoinfty}frac{-z}{z^2-1}sin frac{pi z}{2z+1}=0.$

Получаем ответ: $ointlimits_{|z+1|=1} frac{1}{z^2-1}sin frac{pi z}{2z+1},dz=-2pi i mathop{operatorname{res}}limits_{z=}f(z)=-2pi icdot frac{sqrt{3}}{4}=-frac{ipi}{2}sqrt{3}$ .

Пример 4.33. Вычислить интегралы от многозначных функций:

а) $ointlimits_{|z+2|=frac{3}{2}} frac{sin z}{ln z+3pi i},dz,~ ln(-e)=1-pi i$ ; б) $ointlimits_{|z-1|=frac{3}{2}} frac{z}{ln(z+1)-1},dz$ .

Решение

При вычислении интегралов от многозначной функции предварительно нужно убедиться, что в области, ограниченной контуром интегрирования, подынтегральная функция допускает выделение однозначных ветвей. Это возможно, если точка ветвления многозначного выражения не принадлежит области. Выделение ветви определяется заданием значения функции в некоторой точке области (случай «а»)), если нет такого задания — интеграл вычисляется от всех ветвей (случай «б»)).

а) Точка ветвления z=0 функции ln z не принадлежит кругу $|z+2|< frac{3}{2}$ , и в этой области выражение ln z допускает выделение однозначных ветвей $(ln z)_k=ln|z|+i(arg z+2kpi),~ kin mathbb{Z}$ . Нуль знаменателя — точка $z_0=e^{-3pi i}=-1$ принадлежит кругу $|z+2|< frac{3}{2}$ . Эта точка будет особой точкой для одной из ветвей, а именно для той ветви, для которой ln(-1)=-3pi i . Из условия ln(-e)=1-pi i и (ln z)_k=ln|z|+i(arg z+2kpi) находим kcolon

ln(-e)=ln|-e|+i bigl(cos(-e)+2kpibigr)= 1+i(pi+2kpi)=1-pi i при k=-1 .

Но при этом ln(-1)=ln|-1|+i(pi+2cdot(-1)pi i)=-pi ine-3pi i . Следовательно, для выбранной ветви точка z=-1 не является особой. Поэтому ветвь является в круге $|z+2|< frac{3}{2}$ аналитической и интеграл равен нулю (см. формулу (2.54).

б) Точка ветвления z=-1 функции ln(z+1) не принадлежит кругу $|z-1|< frac{3}{2}$ . В области выделяются однозначные ветви функции ln(z+1)colon

$bigl(ln(z+1)bigr)_k= ln|z+1|+i bigl(arg(z+1)+2kpibigr),quad kin mathbb{Z}.$

Приравнивая нулю знаменатель, находим z+1=e , то есть z=e-1 . Точка принадлежит кругу $|z-1|< frac{3}{2}$ . Так как (ln e)_k=1+i2kpi , то равенство ln(z+1)-1=0 выполняется при z=e-1 только для ветви, для которой k=0 . Для этой ветви точка z_0=e-1 является полюсом первого порядка и вычет в ней вычисляется по формуле (4.24):

$mathop{operatorname{res}}limits_{z=z_0} frac{z}{ln(z+1)-1}= left.{frac{z}{frac{1}{z+1}}}right|_{z=e-1}= e(e-1).$ Получаем ответ: $ointlimits_{|z-1|<frac{3}{2}}f(z),dz= 2pi ie(e-1)$ .

Для других ветвей подынтегральная функция является аналитической и, следовательно, $ointlimits_{|z-1|<frac{3}{2}}f(z),dz=0$ (см. формулу (2.54).

Пример 4.34. Вычислить интеграл от многозначной функции $ointlimits_{|z-4|=2} frac{sqrt{z}}{(z-1)(z-4)},dz$ .

Решение

Точка ветвления z=0 функции sqrt{z} не принадлежит области, по границе которой вычисляется интеграл. Возможно выделение однозначных ветвей и вычисление интеграла с использованием теоремы о вычетах.

Каждая из двух ветвей выражения $sqrt{z}= sqrt{|z|}= exp frac{(arg z+2kpi)i}{2}$ может быть выделена заданием значения функции в одной из точек области. Обозначим, например, $(sqrt{z})_1$ — ветвь, для которой sqrt{4}=2 , и $(sqrt{z})_2$ — ветвь, где overline{4}=-2 . Для каждого случая вычисляем интеграл, т.е.

$ointlimits_{|z-4|=2} f_1(z),dz$ , где $f_1(z)= frac{(sqrt{z})_1}{(z-1)(z-4)}$ , и $ointlimits_{|z-4|=2} f_2(z),dz$ , где $f_2(z)= frac{(sqrt{z})_2}{(z-1)(z-4)}$ .

В обоих случаях в область |z-4|<2 попадает одна особая точка z=4 — Pi(1) . Записываем результат, вычисляя вычет в точке z=4colon

$ointlimits_{|z-4|=2} f_1(z),dz= left.{2pi icdot frac{(sqrt{z})_1}{z-1}}right|_{z=4}= frac{2ipi sqrt{4}}{3}= frac{4pi i}{3},;qquad ointlimits_{|z-4|=2} f_2(z),dz= left.{2pi icdot frac{(sqrt{z})_2}{z-1}}right|_{z=4}= frac{2ipi sqrt{4}}{3}=-frac{4pi i}{3},.$

Пример 4.35. Вычислить интегралы:

a) $ointlimits_{C} frac{sin z}{z^2(z^2+1)^2},dz$ , где — контур, состоящий из дуга окружности $|z|=2,~ operatorname{Im}z geqslant-frac{1}{2}$ и отрезка прямой $operatorname{Im}z=-frac{1}{2}$ (рис. 4.5,а);

б) $ointlimits_{C} frac{dz}{z^4+1}$ , где — контур, состоящий из верхней полуокружности |z|=R,~ R>1,~ operatorname{Im}zgeqslant0 и отрезка действительной оси (рис. 4.5,б).

Рис. 4.5.

Решение

a) В область, ограниченную контуром, входят две особые точки функции: z=0 — Pi(1) и z=i — Pi(2) . Находим вычеты в этих точках:

$begin{aligned}mathop{operatorname{res}}limits_{z=0} frac{sin z}{z^2(z^2+1)^2}&= limlimits_{zto0} frac{sin z}{z(z^2+1)^2}=1;\[4pt] mathop{operatorname{res}}limits_{z=i} frac{sin z}{z^2(z^2+1)^2}&= limlimits_{zto i}! left(frac{sin zcdot (z-i)^2}{z^2(z-i)^2(z^2+i)^2} right)'= limlimits_{zto i}! left(frac{sin z}{z^2(z^2+i)^2}right)'= ldots= frac{operatorname{ch}-3 operatorname{sh}1}{4},. end{aligned}$

Получаем результат: $ointlimits_{C} frac{sin z}{z^2(z^2+1)^2},dz= frac{ipi}{2}(4+operatorname{ch}1-3operatorname{sh}1)$ .

б) В область, ограниченную контуром, попадают две особые точки функции: $z_1=exp frac{ipi}{4}$ и $z_2=exp frac{i3pi}{4}$ (см. пример 4.27). Обе точки — простые полюсы. Находим вычеты функции в этих точках и записываем результат:

$ointlimits_{C} frac{dz}{z^4+1}= 2pi i! left(mathop{operatorname{res}}limits_{z=z_1} frac{1}{z^4+1}+ mathop{operatorname{res}}limits_{z=z_2}frac{1}{z^4+1}right)= 2pi i! left(frac{1}{4z_1^3}+ frac{1}{4z_2^3}right)= frac{2ipi}{4}! left(frac{z_1}{z_1^4}+ frac{z_2}{ z_2^4}right)= ldots= frac{pi sqrt{2}}{2},.$

Здесь учтено, что z_1^4=z_2^4=-1 .

Рассмотренные выше примеры вычисления интегралов от функций комплексного переменного по замкнутому контуру с помощью вычетов показывают преимущество этого метода. Методу соответствует алгоритм, состоящий из несложных процедур. В случае вычисления вычетов в полюсах задача еще более упрощается и сводится к нахождению производных (см. формулы (4.22),(4.24)).

Прежде всего следует ожидать, что можно использовать аппарат вычетов при вычислении определенных интегралов от функции действительной переменной. В самом деле, если подобрать некоторую функцию, переводящую отрезок [a,b] в замкнутую плоскую кривую , то вычисление интеграла $textstyle{intlimits_{a}^{b}f(x),dx}$ можно свести к вычислению интеграла $textstyle{ointlimits_{C}F(z),dz}$ . Простейшая задача такого вида связана с преобразованием отрезка [0;2pi] в окружность.

Интегралы вида $textstyle{intlimits_{0}^{2pi} R(cos x,sin x),dx}$

Здесь R(cos x,sin x)=R(u,v) — рациональная функция аргументов и {v} . Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена $operatorname{tg} frac{x}{2}=t$ («универсальная» подстановка ) и интеграл приводится к интегралу от рациональной дроби, а далее применяется соответствующий алгоритм интегрирования с простыми, но трудоемкими процедурами.

С другой стороны, отрезок [0;2pi] изменения переменных можно рассматривать как изменение arg z точки , принадлежащей окружности. Действительно, замена $z=e^{ix}$ переводит отрезок [0;2pi] в окружность |z|=1,~ 0 leqslantarg z leqslant2pi . При этом для переменных u=cos x и v=sin x получаются несложные, причем рациональные, выражения через . По формулам Эйлера имеем

$cos x=frac{e^{ix}+e^{-ix}}{2},quad sin x=frac{e^{ix}-e^{-ix}}{2i}$ , то есть $cos x=frac{1}{2}! left(z+frac{1}{z}right)!,quad sin x=frac{1}{2i}! left(z-frac{1}{z} right)$ .

Из $e^{ix}=z$ получаем $i,e^{ix},dx=dz$ , a поэтому $dx= frac{dz}{iz}$ . В результате получаем формулу, связывающую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного:

$intlimits_{0}^{2pi}R(cos x,sin x),dx= ointlimits_{|z|=1} R! left(frac{1}{2}! left(z+frac{1}{z}right)!,, frac{1}{2i}! left(z-frac{1}{z}right)right)! frac{dz}{iz},.$

(4.27)

Полученный справа интеграл есть интеграл от рациональной функции, особыми точками которой являются только полюсы.

Пример 4.36. Вычислить собственный интеграл $intlimits_{0}^{2pi} frac{dx}{(5+4cos x)^2}$ с помощью вычетов.

Решение

Вычисление несобственных интегралов с помощью вычетов

Еще больший интерес представляет возможность применения вычетов для вычисления несобственных интегралов вида $textstyle{intlimits_{-infty}^{+infty} f(x)dx}$ , где интеграл понимается в смысле главного значения, т.е. $textstyle{intlimits_{-infty}^{+infty} f(x)dx= limlimits_{Rtoinfty} intlimits_{-R}^{R}f(x)dx}$ (здесь отрезок [a,b]=[-R,R] ). Будем рассматривать функцию f(x) , непрерывную на (-infty,+infty) . Возможность использования вычетов при решении такой задачи основана на том, что отрезок [-R,R] действительной оси рассматривается как часть замкнутого контура , состоящего из этого отрезка и дуги окружности, а интеграл по контуру записывается в виде суммы:

$ointlimits_{C} f(z),dz= intlimits_{-R}^{R}f(x),dx+ intlimits_{C_R}f(z),dz$ , где C_R — дуга окружности |z|=R,~ operatorname{Im}zgeqslant0 .

Несобственный интеграл $textstyle{intlimits_{-infty}^{+infty} f(x)dx}$ определяется как предел:

$intlimits_{-infty}^{+infty} f(x),dx= ointlimits_{C}f(z),dz-limlimits_{Rtoinfty} intlimits_{C_R}f(z),dz,.$

Пример 4.37. Вычислить несобственный интеграл $intlimits_{-infty}^{+infty} frac{dx}{x^4+1}$ , используя вычеты.

Решение

Рассмотрим контур , состоящий из дуги C_R — окружности |z|=R,~ operatorname{Im}z geqslant0 и отрезка [-R,R] . Для функции $f(z)=frac{1}{z^4+1}$ имеем

$ointlimits_{C} frac{dz}{z^4+1}= 2pi i! left(mathop{operatorname{res}}limits_{z=z_1}f(z)+ mathop{operatorname{res}}limits_{z=z_2}f(z) right)= frac{pi sqrt{2}}{2}$ (см. пример 4.35 п.»б»).

С другой стороны,

$ointlimits_{C}f(z),dz= intlimits_{-R}^{R}f(z),dz+ ointlimits_{C_R} f(z),dz$ , или $intlimits_{-R}^{R} frac{dx}{x^4+1}= ointlimits_{C} frac{dz}{z^4+1}-intlimits_{C_R} frac{dz}{z^4+1}$ .

Оценим интеграл по дуге, учитывая неравенство для подынтегральной функции

$left|frac{1}{z^4+1}right|= frac{1}{|z^4+1|}< frac{1}{|z|^4-1}$ , то есть $frac{1}{|z^4+1|}< frac{1}{R^4-1}$ для zin C_R , где |z|=R .

Получаем $Biggl|intlimits_{C_R} frac{dz}{z^4+1}Biggr|< intlimits_{C_R} left|frac{dz}{z^4+1}right|< frac{1}{R^4-1} intlimits_{C_R} |dz|= frac{pi R}{R^4-1}$ , поэтому $intlimits_{Rtoinfty} intlimits_{C_R} frac{dz}{z^4+1}=0$ .

В результате $limlimits_{Rtoinfty} intlimits_{-R}^{R} frac{dx}{x^4+1}= ointlimits_{C} frac{dz}{z^4+1}= frac{pi sqrt{2}}{2}$ , то есть $intlimits_{-infty}^{+infty} frac{dx}{x^4+1}= frac{pi sqrt{2}}{2}$ .

Интерес, с точки зрения применения вычетов, представляют интегралы $textstyle{intlimits_{-infty}^{+infty} f(x)dx}$ , где функция f(x) такова, что $textstyle{limlimits_{Rtoinfty} intlimits_{C_R} f(z)dz=0}$ , как в рассмотренном примере. Классы таких функций выделяются, и для всех функций рассматриваемого класса устанавливается формула $textstyle{intlimits_{-infty}^{+infty} f(x),dx= ointlimits_{C} f(z)dz}$ .

Интегралы вида $textstyle{intlimits_{-infty}^{+infty} R(x),dx}$

Здесь R(x) — рациональная функция переменной , то есть $R(x)= frac{P_n(x)}{Q_m(x)}$ , где P_n(x) и Q_m(x) — многочлены степени и соответственно. Как отмечалось выше, рассматриваем функцию R(x) , непрерывную на (-infty,+infty) , т.е. многочлен Q_m(x) не имеет действительных нулей. В теории несобственных интегралов путем сравнения таких интегралов с интегралами $textstyle{intlimits_{a}^{+infty} dfrac{dx}{x^{alpha}},~ a>0}$ , устанавливается их сходимость при условии m-n>1 , то есть m-n geqslant2 . При таком условии $limlimits_{ztoinfty} R(z)=0$ и функция R(z) , доопределенная в точке z=infty предельным значением R(infty)=0 , имеет в этой точке нуль порядка не ниже второго, а поэтому может быть записана в виде $R(z)= frac{alpha(z)}{z}$ , где $limlimits_{ztoinfty} alpha(z)=0$ , то есть |alpha(z)|<varepsilon при |z|toinfty .

Учитывая это, проводим оценку интеграла, как в рассмотренном примере,

$Biggl|intlimits_{C_R} R(z),dzBiggr|< intlimits_{C_R} frac{|alpha(z)|}{|z|},|dz|= frac{1}{R} intlimits_{C_R} |alpha(z)||dz|= frac{varepsilon}{R},pi R= varepsilonpi$ и получаем $limlimits_{Rtoinfty} intlimits_{C_R} R(z),dz=0$ .

Таким образом, для рассматриваемого типа интегралов получаем $intlimits_{-infty}^{+infty} R(x),dx= ointlimits_{C} f(z),dz$ , где — контур, состоящий из верхней полуокружности |z|=R,~ operatorname{Im}zgeqslant0 и отрезка [-R,R] , причем таково, что все особые точки функции f(z) , для которых operatorname{Im}z>0 , расположены в полукруге |z|<R,~ operatorname{Im}z geqslant0 .

Очевидно, аналогичный вывод можно получить, рассматривая полукруг |z|<R,~ operatorname{Im}z<0 .

Результаты приведенных рассуждений запишем в виде утверждения.

Утверждение 4.9. Пусть функция $R(x)= frac{P_n(x)}{Q_m(x)}$ , удовлетворяет условиям:
1) m-ngeqslant2 , т.е. степень знаменателя больше степени числителя по крайней мере на два;
2) Q_m(x)ne0 для — действительных, т. е. R(z) не имеет особых точек на действительной оси.

Тогда справедливы равенства:

$intlimits_{-infty}^{+infty} R(x),dx= 2pi i sum_{k=1}^{p} mathop{operatorname{res}}limits_{z=z_k} R(z),quad operatorname{Im}z_k>0,$

(4.28)

$intlimits_{-infty}^{+infty} R(x),dx=-2pi i sum_{k=1}^{p} mathop{operatorname{res}}limits_{z=z_k} R(z),quad operatorname{Im}z_k<0.$

(4.29)

где z_k,~k=1,2,ldots,p — все особые точки функции R(z) , расположенные выше оси $Ox~(operatorname{Im}z_k>0)$ в случае формулы (4.28) и ниже оси $Ox~(operatorname{Im}z_k<0)$ — в случае формуль (4.29).

Заметим, что если R(x) — четная функция, то можно, используя эти формулы, вычислять интегралы вида $textstyle{intlimits_{0}^{+infty} f(x),dx}$ , так как для четных функций имеет место равенство $textstyle{intlimits_{-R}^{R} f(x),dx= 2 intlimits_{0}^{R} f(x),dx}$ .

Алгоритм вычисления несобственных интегралов с помощью вычетов

1. Проверить условия применения формулы (4.28) или (4.29) (см. утверждение 4.9).
2. Найти особые точки подынтегральной функции R(x) .
3. Вычислить вычеты в особых точках функции R(x) , расположенных:

а) выше оси , если применяется формула (4.28);
б) ниже оси , если применяется формула (4.29).

4. Записать результат по формуле (4.28) или (4.29).

▼ Примеры 4.38-4.39

Пример 4.38. Вычислить интегралы: а) $intlimits_{-infty}^{+infty} frac{x^2+3}{(x^2+2x+17)^2},dx$ ; б) $intlimits_{0}^{+infty} frac{x^2,dx}{(x^2+4)^3}$ .

Решение

а) Воспользуемся алгоритмом.

1. Проверяем условия утверждения 4.9:

– так как в числителе многочлен степени n=2 , а в знаменателе m=4 , то условие m-ngeqslant2 выполняется;

– уравнение x^2+2x+17=0 не имеет действительных корней, так как дискриминант трехчлена D<0 . Поэтому второе условие также выполняется.

2. Особыми точками функции $f(z)= frac{z^2+3}{(z^2+2z+17)^2}$ являются полюсы второго порядка z_1=1+4i и z_2=1-4i .

3. Применим формулу (4.28). Для этого вычислим вычет в точке $z_1in operatorname{Im}z>0colon$

$begin{aligned}mathop{operatorname{res}}limits_{z=z_1} frac{z^2+3}{(z-z_1)^2(z-z_2)^2}&= limlimits_{zto z_1}! left(frac{(z^2+3)(z-z_1)^2}{(z-z_1)^2(z-z_2)^2}right)'= limlimits_{zto z_1}! left(frac{z^2+3}{(z-z_2)^2}right)'= limlimits_{zto z_1}frac{2z^2-2zz_2-2z^2-6}{(z-z_2)^3}=\ &= left.{frac{-2zz_2-6}{(z-z_2)^3}}right|_{z=z_1}= frac{-2z_1z_2-6}{(z_1-z_2)^3}= ldots= frac{5}{16i},.end{aligned}$

4. Записываем ответ: $intlimits_{-infty}^{+infty} frac{x^2+3}{(x^2+2x+17)^2},dx$ .

б) Воспользуемся алгоритмом.

1. Условия утверждения 4.9 выполняются. Можно использовать формулу (4.28). Подынтегральная функция является четной.

2. Особыми точками функции $f(z)= frac{z^2}{(z^2+4)^3}$ являются полюсы третьего порядка z_1=2i и z_2=-2i .

3. Находим вычет в точке z_1colon

$begin{aligned}mathop{operatorname{res}}limits_{z=z_1}frac{z^2}{(z^2+4)^3}&= frac{1}{2} limlimits_{zto z_1}! left(frac{z^2(z-2i)^3}{(z-2i)^3(z+2i)^3}right)''= frac{1}{2}limlimits_{zto z_1} frac{(4i-2z)(z+2i)^4-4(4iz-z^2)(z+2i)^3}{(z+2i)^8}=\ &=left.{frac{1}{2}cdot frac{2(2i-z)(2i+z)-4z(4i-z)}{(z+2i)^5}}right|_{z=z_1}= frac{-2cdot2icdot2i}{(4i)^5}= frac{8}{4^5i},.end{aligned}$

4. Записываем ответ: $intlimits_{0}^{+infty} frac{x^2}{(x^2+4)^3},dx= frac{1}{2}intlimits_{-infty}^{+infty} frac{x^2}{(x^2+4)^3},dx= pi i mathop{operatorname{res}}limits_{z=2i}f(z)= pi icdot frac{8}{4^5i}= frac{pi}{128}$ .

Пример 4.39. Вычислить несобственные интегралы с помощью вычетов:

а) $intlimits_{-infty}^{+infty} frac{dx}{(x^2+1)(x^2-ix-1)^2}$ ; б) $intlimits_{0}^{+infty}frac{dx}{x^4-2i}$ .

Решение

Условия применения формул вычисления интегралов с помощью вычетов выполняются.

Заметим, что в отличие от предыдущих примеров здесь подынтегральные функции являются комплекснозначными и $textstyle{intlimits_{-infty}^{+infty} f(x),dx}$ может быть комплексным числом.

а) Особыми точками функции $f(z)=frac{1}{(z^2+1)(z^2-iz-1)^2}$ являются z_1=i,~ z_2=-i , и корни уравнения z^2-iz-1=0 , то есть $z_3=frac{i+ sqrt{3}}{2}$ и $z_4=frac{i-sqrt{3}}{2}$ . Три точки расположены в верхней полуплоскости, одна z=-i — в нижней. Будем применять формулу (4.29). Вычисляем вычет в точке z=-i — простом полюсе подынтегральной функции по формуле (4.24):

$mathop{operatorname{res}}limits_{z=-i} frac{dfrac{1}{(z^2-iz-1)^2}}{z^2+1}= left.{ dfrac{1}{2z(z^2-iz-1)^2}}right|_{z=-i}= frac{1}{(-2i)(-1-1-1)^2}= frac{-1}{18i},.$

Получаем ответ: $intlimits_{-infty}^{+infty} frac{dx}{(x^2+1)(x^2-ix-1)^2}=-2pi i mathop{operatorname{res}}limits_{z=-i}f(z)=frac{pi}{9}$ .

б) Особыми точками функции $f(z)=frac{1}{z^4-2i}$ являются корни уравнения z^4=2i , то есть $z_k=sqrt[LARGE{4}]{2}expleft[left(frac{pi}{8}+ frac{pi}{2}kright)!i right],~ k=0,1,2,3$ . Все особые точки — простые полюсы функции; две расположены в верхней полуплоскости, две — в нижней. Используем формулу (4.28), рассмотрим точки $z_1= sqrt[LARGE{4}]{2}exp frac{ipi}{8}$ и $z_2=sqrt[LARGE{LARGE{4}}]{2}exp frac{i5pi}{8}=sqrt[LARGE{LARGE{4}}]{2}exp frac{ipi}{8}exp frac{ipi}{2}=icdot z_1$ .

Вычисляя вычеты по формуле (4.24), записываем результат (при этом учитывается, что z_1^4=z_2^4=2i ):

$intlimits_{0}^{+infty}frac{dx}{x^4-2i}= ipi! left(mathop{operatorname{res}}limits_{z=z_1} frac{1}{x^4-2i}+ mathop{operatorname{res}}limits_{z=z_2} frac{1}{x^4-2i}right)= ipi! left(frac{1}{4z_1^3}+ frac{1}{4z_2^3}right)= frac{ipi}{4}! left(frac{z_1}{z_1^4}+ frac{z_2}{z_2^4}right)= frac{ipi}{4cdot2i}(z_1+z_2)= frac{pi}{8}(1+i)exp frac{ipi}{8},.$

или, так как $1+i=exp frac{ipi}{4}$ , то $intlimits_{0}^{+infty} frac{dx}{x^4-2i}= frac{pi}{8}exp frac{i3pi}{8}$ .

Несобственные интегралы вида $textstyle{intlimits_{-infty}^{+infty}e^{ilambda x}R(x),dx}$

Выше рассматривались интегралы вида $textstyle{intlimits_{-infty}^{+infty} R(x),dx}$ , где $R(x)=frac{P_n(x)}{Q_m(x)},~ m-ngeqslant2$ и Q_m(x)ne0 для zin R . Но такими интегралами не исчерпывается класс сходящихся несобственных интегралов $textstyle{intlimits_{-infty}^{+infty} f(x),dx}$ .

Например, сходящимися, согласно признаку Абеля, являются интегралы $textstyle{intlimits_{a}^{+infty} f(x),dx}$ , где f(x)=varphi(x)cdot g(x) и функции varphi(x),~g(x) удовлетворяют условиям:

а) varphi(x) непрерывна и имеет ограниченную первообразную на [a;+infty) , т.е. для любого Ageqslant a справедливо неравенство $textstyle{left|intlimits_{a}^{A} varphi(x),dxright|<M}$ ;

б) g(x) — непрерывно дифференцируема на [a;+infty) и, монотонно убывая, стремится к нулю при xto+infty , то есть

$limlimits_{xto+infty} g(x)=0,quad g'(x)=0,quad xin[a;+infty).$

▼ Пример 4.40

Пример 4.40. Исследовать сходимость интегралов:

а) $intlimits_{a}^{+infty} sin x,dx,quad intlimits_{a}^{+infty} cos x,dx,quad intlimits_{a}^{+infty} frac{dx}{x},quad intlimits_{0}^{+infty}frac{x,dx}{1+x^2} ;$

б) $intlimits_{a}^{+infty} frac{sin x}{x},dx,quad intlimits_{a}^{+infty} frac{cos x}{x},dx,quad intlimits_{a}^{+infty} frac{xsin x}{1+x^2},dx,quad intlimits_{a}^{+infty} frac{xcos x}{1+x^2},dx,~ a>0;$

в) $intlimits_{-infty}^{+infty} frac{xcos x}{1+x^2},dx,quad intlimits_{-infty}^{+infty} frac{xsin x}{1+x^2},dx,.$

Решение

В качестве обобщения можно на основании признака Абеля сделать заключение, что сходящимися являются интегралы вида

$intlimits_{-infty}^{+infty} R(x)coslambda x,dx,quad intlimits_{-infty}^{+infty} R(x)sinlambda x,dx$ , где $R(x)=frac{P_n(x)}{Q_m(x)},~m-ngeqslant1$ и Q_m(x)ne0 для xinmathbb{R} .

Вычисление таких интегралов и приводящихся к ним интегралов методам математического анализа (нахождение первообразной) представляет в большинстве случаев определенные трудности.

Воспользуемся предложенным выше приемом сведения вычисления несобственного интеграла $textstyle{intlimits_{-infty}^{+infty} f(x),dx}$ к вычислению интеграла по замкнутому контуру от функции комплексного переменного:

$intlimits_{-infty}^{+infty} f(x),dx= ointlimits_{C}f(z),dz-limlimits_{Rtoinfty} ointlimits_{C_R} f(z),dz,.$

Заметим, что запись $textstyle{intlimits_{-infty}^{+infty} f(x),dx= ointlimits_{C} f(z),dz}$ без исследования, в частности без доказательства равенства $textstyle{limlimits_{Rtoinfty} ointlimits_{C_R} f(z),dz}$ , не имеет основания и может привести к ошибкам. Так, для интеграла из примера 4.40 имеем

$intlimits_{-infty}^{+infty} f(x),dx= intlimits_{-infty}^{+infty} frac{xcos x}{1+x^2},dx=0$ , но $mathop{operatorname{res}}limits_{z=i} frac{zcos z}{1+z^2}= frac{icos i}{2i}= frac{operatorname{ch}1}{2}$ и $ointlimits_{C} f(z),dz=ipi operatorname{ch}1$ ,

где — контур, состоящий из дуги |z|=R,~ R>1,~ operatorname{Im}z geqslant 0 и отрезка [-R;R] . Поэтому в данном случае $textstyle{intlimits_{-infty}^{+infty} f(x),dxne ointlimits_{C} f(z),dz}$ .

Будем рассматривать $textstyle{intlimits_{-infty}^{+infty} f(x),dx}$ , где $f(x)=R(x)e^{ilambda x}$ и $R(x)= frac{P_n(x)}{Q_m(x)},~m-n geqslant 1$ и Q_m(x)ne0,~ xin R , а R(x) принимает действительные значения. Такой интеграл сходится, так как он может быть записан в виде суммы двух сходящихся интегралов:

$intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx= intlimits_{-infty}^{+infty} R(x)coslambda x,dx+ iintlimits_{-infty}^{+infty} R(x)sinlambda x,dx,.$

(4.30)

Лемма Жордана

Доказательство возможности применения вычетов к вычислению интеграла $textstyle{intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx}$ основано на следующем утверждении.

Утверждение Жордана (4.10). Пусть функция f(z) непрерывна в области $Dcolon, |z| geqslant R_0,~ operatorname{Im}z geqslant-a$ и $limlimits_{Rtoinfty} max_{C_R}|f(z)|=0$ , где C_R — дуга окружности |z|=R,~ operatorname{Im}zgeqslant-a . Тогда для любого lambda>0 справедливо равенство

$limlimits_{Rtoinfty} intlimits_{C_R} e^{ilambda z}f(z),dz=0.$

(4.31)

Замечания 4.7

1. Формула (4.31) верна для любого действительного . На рис. 4.6 изображены контур и дуга C_R для случаев a>0,~ a=0,~a<0 .

Рис. 4.6.

2. Формула (4.31) верна и при любом lambda<0 . При этом C_R — дуга окружности |z|=R,~ operatorname{Im}z leqslant a . Справедливость этого заключения получается из леммы пуnем замены на (-z) , что в силу $(-z)=z,e^{ipi}$ геометрически соответствует повороту на (рис. 4.7).

Рис. 4.7.

3. Большой интерес в приложениях представляет запись леммы, получаемая заменой iz=p . Геометрически это соответствует повороту на угол $frac{pi}{2}$ , так как $p=zexp frac{ipi}{2}$ . Для дуг окружностей C_Rcolon 1) $C_Rcolon |p|=R,~ operatorname{Re}p leqslant a$ при t>0 и 2) $C_Rcolon |p|=R,~ operatorname{Re}p geqslant-a$ при t<0 (рис. 4.8) имеет место формула

$limlimits_{Rtoinfty} intlimits_{C_R} F(p)e^{p,t},dp=0.$

(4.32)

Рис. 4.8.

В частном случае a=0 (см. рис. 4.6,б и рис. 4.7,б) лемма применяется для вычисления интегралов $textstyle{intlimits_{-infty}^{+infty} f(x)e^{ilambda x},dx}$ с помощью вычетов. Кроме того, если функция f(x) принимает только действительные значения при xinmathbb{R} , то, используя равенство (4.30), получаем возможность вычислять с помощью вычетов интегралы $textstyle{intlimits_{-infty}^{+infty} f(x)coslambda x,dx}$ и $textstyle{intlimits_{-infty}^{+infty} f(x)sinlambda x,dx}$ . Первый из них является действительной частью, второй — мнимой частью интеграла $textstyle{intlimits_{-infty}^{+infty} f(x)e^{ilambda x},dx}$ .

Для рассматриваемых в данном пункте интегралов $textstyle{intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx}$ функция f(z)=R(z) удовлетворяет лемме Жордана. Подводя итог приведенным рассуждениям, запишем следующее утверждение.

Утверждение 4.11. Пусть R(x) — рациональная функция, не имеющая особых точек на действительной оси (т.е. Q(x)ne0 для xinmathbb{R} ), для которой точка z=infty — нуль порядка не ниже первого (т.е. m-ngeqslant1 ). Тогда справедливы формулы:

1) при lambda>0

$intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx= 2ipi sum_{k=1}^{n} mathop{operatorname{res}}limits_{z=z_k} bigl[R(z)e^{ilambda z}bigr],quad operatorname{Im} z_k>0;$

(4.33)

2) при lambda<0

$intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx=-2ipisum_{k=1}^{n} mathop{operatorname{res}}limits_{z=z_k} bigl[R(z)e^{ilambda z}bigr],quad operatorname{Im} z_k<0;$

(4.34)

3) при lambda>0

$intlimits_{-infty}^{+infty} f(x)coslambda x,dx=-2pi operatorname{Im}! left(sum_{k=1}^{n} mathop{operatorname{res}}limits_{z=z_k} bigl[R(z)e^{ilambda z}bigr] right)!,quad operatorname{Im}z_k>0,$

(4.35)

$intlimits_{-infty}^{+infty} f(x)sinlambda x,dx= 2pioperatorname{Im}! left(sum_{k=1}^{n} mathop{operatorname{res}}limits_{z=z_k} bigl[R(z)e^{ilambda z}bigr] right)!,quad operatorname{Im}z_k>0.$

(4.36)

Алгоритм вычисления интегралов $textstyle{intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx}$

1. Проверить условия для функции R(x) , записанные в утверждении 4.11.
2. Вычислить вычеты функции $R(z)e^{ilambda z}$ во всех ее особых точках:

а) лежащих выше оси , в случае lambda>0 ;
б) лежащих ниже оси , в случае lambda<0 .

3. Записать результат по формуле (4.33) при lambda>0 и по (4.34) при lambda<0 .

4. Для вычисления интегралов $textstyle{intlimits_{-infty}^{+infty} f(x)coslambda x,dx}$ и $textstyle{intlimits_{-infty}^{+infty} f(x)sinlambda x,dx}$ в результате, полученном в п. 3, отделить действительную и мнимую части и записать ответы для указанных интегралов по формулам (4.35) и (4.36).

▼ Примеры 4.41-4.43

Пример 4.41. Вычислить несобственные интегралы: а) $intlimits_{0}^{+infty} frac{xsin x}{1+x^2},dx$ ; б) $intlimits_{-infty}^{+infty} frac{(x+1)cos x}{x^2-2x+2},dx$ .

Решение

Приведем интегралы к виду $textstyle{intlimits_{-infty}^{+infty} R(x)e^{ilambda x},dx}$ и воспользуемся алгоритмом.

а) Так как подынтегральная функция четная, то можно записать

$textstyle{intlimits_{0}^{+infty} dfrac{xsin x}{1+x^2},dx= dfrac{1}{2}intlimits_{-infty}^{+infty} dfrac{xsin x}{1+x^2},dx}$ . Введем функцию $f(x)= R(x)e^{ix}$ , для которой $dfrac{xsin x}{1+x^2}$ является мнимой частью, т.е. рассмотрим $textstyle{intlimits_{-infty}^{+infty} frac{x,e^{ix}}{1+x^2},dx}$ .

1. Функция $R(x)= frac{x}{1+x^2}$ удовлетворяет условиям: m-n=2-1=1;~ 1+x^2ne0 для действительных .

2. Так как здесь lambda=1>0 , применяем формулу (4.33) или (4.36), т.е. рассматриваем только те особые точки функции f(z) , которые лежат выше оси . Функция $R(z)= frac{z}{1+z^2}$ имеет две особые точки: z_1=i и z_2=-i . Используя (4.24), вычисляем вычет в точке z=i — простом полюсе:

$mathop{operatorname{res}}limits_{z=i} frac{z}{1+z^2},e^{iz}= left.{frac{z}{2z},e^{iz}}right|_{z=i}= frac{1}{2},e^{-1}.$

Так как $operatorname{Re} mathop{operatorname{res}}limits_{z=i} frac{z}{1+z^2},e^{iz} = frac{e^{-1}}{2}$ , то по формуле (4.36) записываем ответ:

$intlimits_{0}^{+infty} frac{xsin x}{1+x^2},dx= frac{1}{2} intlimits_{-infty}^{+infty} frac{xsin x}{1+x^2},dx= frac{1}{2}cdot 2picdot frac{e^{-1}}{2}= frac{pi}{2},e^{-1}.$

б) Рассматриваем интеграл $textstyle{intlimits_{-infty}^{+infty} dfrac{(x+1)e^{ix}}{x^2-2x+2},dx}$ .

1. Условия применения формул выполняются: функция $R(z)= frac{z+1}{z^2-2z+2}$ в точке z=infty имеет нуль порядка n=1 и на действительной оси не имеет особых точек. Особые точки функции: z_1=1+i,~ z_2=1-i .

2. Так как lambda=1>0 , вычисляем вычет в точке z_1=1+i — простом полюсе функции по формуле (4.24):

$mathop{operatorname{res}}limits_{z=z_1} frac{z+1}{z^2-2z+2},e^{iz}= left.{frac{z+1}{2z-2},e^{iz}}right|_{z_1}= frac{2+i}{2i},e^{i-1}.$

3. Для интеграла $textstyle{intlimits_{-infty}^{+infty} dfrac{(x+1)e^{ix}}{x^2-2x+2},dx}$ по формуле (4.33) получаем результат:

$2ipicdot frac{2+i}{2i},e^{i-1}= pi,e^{-1}(2+i)e^{i}= pi,e^{-1}(2+i)(cos1+ isin1).$

4. Записываем ответ: $intlimits_{-infty}^{+infty} frac{(x+1)cos x}{x^2-2x+2},dx= operatorname{Re} intlimits_{-infty}^{+infty} dfrac{(x+1)e^{ix}}{x^2-2x+2},dx= operatorname{Re} bigl(pi,e^{-1}(2+i)e^{i}bigr)= pi,e^{-1}(2cos1-sin1)$ .

Используя формулу (4.35), пп. 3,4 можно объединить:

$intlimits_{-infty}^{+infty} frac{(x+1)cos x}{x^2-2x+2},dx=-2pi operatorname{Im} frac{2+i}{2i},e^{i-1}.$

где $frac{2+i}{2i},e^{i-1}= frac{1}{2}(1-2i)e^{-1}(cos1+isin1)= frac{1}{2},e^{1} bigl[(cos1+2sin1)+i(-2cos1+sin1)bigr]$ ;

$operatorname{Im} frac{2+i}{2i},e^{i-1}= frac{1}{2},e^{-1}(sin1-2cos1).$

В результате получаем ответ: $pi,e^{-1}(2cos1-sin1)$ .

Пример 4.42. Вычислить несобственный интеграл $intlimits_{-infty}^{+infty} frac{cos5x}{(x^2+1)^2(x^2+4)},dx$ .

Решение

Пример 4.43. Вычислить интегралы: а) $intlimits_{-infty}^{+infty} frac{e^{ix},dx}{(x^2+2ix-2)^2}$ ; б) $intlimits_{-infty}^{+infty} frac{e^{ix} sqrt{x+i}}{x^2+1},dx,~ Bigl.{sqrt{z+i}}Bigr|_{z=0}=exp frac{ipi}{4}$ .

Решение

а) Применяем формулу (4.33), так как lambda=1>0 , т.е. рассматриваем только точки верхней полуплоскости.

Но обе особые точки функции $f(z)= frac{1}{z^2+2iz-2}$ , точки $z_1=-i+sqrt{3}$ и $z_2=-i-sqrt{3}$ расположены в нижней полуплоскости. Поэтому интеграл равен нулю.

б) Требуется, как и в предыдущем пункте, вычислить интеграл от комплекснозначной функции действительной переменной. При вычислении рассматривается та ветвь двузначного выражения sqrt{z+i} , для которой задано значение в точке $sqrt{i}=exp frac{ipi}{4}$ .

Функция $R(z)= frac{sqrt{z+i}}{z^2+1}$ удовлетворяет условиям применения формулы (4.33). Так как здесь lambda=1>0 , рассматриваем вычет в точке z=icolon

$mathop{operatorname{res}}limits_{z=i} frac{e^{iz} sqrt{z+i}}{z^2+1}= ldots= left.{ frac{e^{iz} sqrt{z+i}}{2z}}right|_{z=i}= frac{e^{-1}}{2i} sqrt{2i}= frac{e^{-1}}{2i} sqrt{2}exp frac{ipi}{4},.$

Получаем ответ: $intlimits_{-infty}^{+infty} frac{e^{ix} sqrt{x+i}}{x^2+1},dx= 2pi icdot frac{e^{-1}}{2i} sqrt{2}exp frac{ipi}{4}= pi e^{-1}(1+i).$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Download Article

Contour integration is integration along a path in the complex plane. The process of contour integration is very similar to calculating line integrals in multivariable calculus. As with the real integrals, contour integrals have a corresponding fundamental theorem, provided that the antiderivative of the integrand is known.

In this article, we will go over one of the most important methods of contour integration, direct parameterization, as well as the fundamental theorem of contour integrals. To avoid pathological examples, we will only consider contours that are rectifiable curves that are defined in a domain continuous, smooth, one-to-one, and whose derivative is non-zero everywhere on the interval. Read on for a guide on calculating contour integrals.

1

Apply the Riemann sum definition for contour integrals.
2

Rewrite the contour integral in terms of the parameter .

Advertisement
3

Parameterize and calculate ${frac {{mathrm {d}}z}{{mathrm {d}}t}}$ .
4

Evaluate. We know that is real-valued, so all that remains is to integrate using the standard integration techniques of real-variable calculus.

1
2
3

Calculate ${frac {{mathrm {d}}z}{{mathrm {d}}t}}$ . Substitute our results into the integral.
4
Evaluate.
- ${begin{aligned}int _{{0}}^{{1}}(t^{{3}}+i2t^{{2}})(1+i){mathrm {d}}t&=int _{{0}}^{{1}}(t^{{3}}+i2t^{{2}}+it^{{3}}-2t^{{2}}){mathrm {d}}t\&={frac {1}{4}}+ileft({frac {2}{3}}+{frac {1}{4}}right)-{frac {2}{3}}\&=-{frac {5}{12}}+{frac {11}{12}}iend{aligned}}$
5

1

Generalize the Fundamental Theorem of Calculus. As it pertains to contour integrals, the theorem is used to easily compute the value of contour integrals so long as we can find an antiderivative. The proof of this theorem is similar to all other fundamental theorem of calculus proofs, but we will not state it here for brevity.
2
3

Parameterize find ${frac {{mathrm {d}}z}{{mathrm {d}}t}},$ and evaluate.
4

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

About This Article

Thanks to all authors for creating a page that has been read 31,103 times.

Did this article help you?

Get all the best how-tos!

You’re all set!

Источник

Теоретический минимум

Часто встречаются случаи, когда вычисление определённых интегралов методами комплексного анализа предпочтительнее, чем методами
вещественного анализа. Причины могут быть самыми разными. Методы ТФКП могут позволять в отдельных случаях сильно сократить вычисления.
Иногда формулу Ньютона-Лейбница нельзя использовать, так как неопределённый интеграл не выражается в элементарных функциях.
Методы дифференцирования и интегрирования по параметру требуют очень аккуратного обоснования своей применимости, да и параметр иногда
приходится вводить искусственно.

Обычно методами комплексного анализа вычисляются несобственные интегралы — по бесконечному промежутку или от неограниченных на отрезке
интегрирования функций. Общая идея заключается в следующем. Составляется контурный интеграл. Интеграл по некоторым участкам контура должен
совпадать с искомым определённым интегралом — по крайней мере, с точностью до постоянного множителя. Интегралы по остальным участкам контура
должны вычисляться. Затем применяется основная теорема о вычетах, согласно которой
,
где — это особые точки функции , находящиеся внутри контура интегрирования . Таким образом, контурный интеграл с одной
стороны оказывается выраженным через искомый определённый интеграл, а с другой стороны вычисляется с помощью вычетов (что обычно
серьёзных сложностей не представляет).

Основная сложность — выбор контура интегрирования. Его подсказывает, в принципе говоря, подынтегральная функция. Однако без достаточной
практики овладеть данным методом сложно, а потому примеров будет приведено довольно много. Наиболее часто используются контуры, составленные из
элементов, по которым удобно проводить интегрирование (прямые, дуги окружностей).

Примеры вычисления определённых интегралов с помощью контурного
интегрирования в комплексной плоскости

Пример 1. Интегралы Френеля.
Вычислим интегралы , .
Несложно догадаться, что первым шагом является переход к экспоненциальной форме, предполагающий рассмотрение интеграла .
Нужно только подобрать контур интегрирования. Понятно, что в контур должна войти полуось . Вещественная и
мнимая части интеграла по этой части контура представляют собой интегралы Френеля. Далее, вычисляемый контурный интеграл по структуре
подынтегрального выражения напоминает интеграл Эйлера-Пуассона, значение которого известно. Но чтобы получить этот интеграл, нужно положить
, тогда . А такое представление переменной — это интегрирование по прямой, проходящей через точку
под углом к вещественной оси.
Итак, два элемента контура есть. Чтобы контур замкнулся, будем считать, что выбранные два участка контура имеют конечную длину , и замкнём
контур дугой окружности радиуса . Позже мы устремим этот радиус к бесконечности. В результате получается изображённый на рис. 1 контур.

(1)
Внутри контура интегрирования подынтегральная функция особых точек не имеет, поэтому интеграл по всему контуру равен нулю.
На участке можно записать , тогда
.
В пределе этот интеграл равен нулю.
На участке можно записать , тогда
.
Подставляем полученные результаты в (1) и переходим к пределу :

Отделяя вещественную и мнимую части, находим, учитывая значение интеграла Эйлера-Пуассона
,
.

Пример 2. Выбор контура интегрирования, содержащего внутри особую точку подынтегральной функции.
Вычислим интеграл, похожий на рассмотренный в первом примере: , где .
Вычислять будем интеграл . Контур выберем аналогичный тому, который использовался в первом примере. Только теперь нет цели
свести вычисление к интегралу Эйлера-Пуассона. Здесь заметим, что при замене подынтегральная функция не изменится.
Это соображение подсказывает выбрать наклонную прямую контура интегрирования так, чтобы она составляла с вещественной осью угол .

При записи контурного интеграла
(2)
интеграл по дуге окружности в пределе стремится к нулю. На участке можно записать :
.
Таким образом, из (2) при переходе к пределу находим
.
Здесь учтено, что внутри контура интегрирования подынтегральная функция имеет простой полюс .

Отсюда находим искомый интеграл:
.

Пример 3. Через верхнюю или нижнюю полуплоскость замкнуть контур интегрирования?
На следующем достаточно простом интеграле продемонстрируем характерную деталь выбора контура интегрирования. Вычислим
интеграл .
Фактически искомый интеграл функции вычисляется вдоль вещественной оси, на которой подынтегральная функция не имеет
особенностей. Остаётся только замкнуть контур интегрирования. Так как у функции под интегралом всего две конечные особые точки, то
замкнуть контур можно полуокружностью, радиус которой следует устремить к бесконечности. И здесь возникает вопрос о том, как должна
быть выбрана полуокружность: в верхней или нижней полуплоскости (см. рис. 3 а, б). Чтобы понять это, запишем интеграл по полуокружности
в обоих случаях:

а)
б)
Как видно, поведение интеграла в пределе определяется множителем .
В случае «а» , а потому предел будет конечен при условии .
В случае «б» — напротив — , а потому предел будет конечен при условии .
Это наводит на мысль, что способ замыкания контура определяется знаком параметра . Если он положителен, то
контур замыкается через верхнюю полуплоскость, в противном случае — через нижнюю. Рассмотрим эти случаи отдельно.
а)
Интеграл по полуокружности в пределе , как мы видели, обратится в нуль. Внутри контура (см. рис. 3а) находится
особая точка , поэтому

б)
Аналогично находим с помощью интегрирования по контуру, изображённому на рис. 3б,

Замечание. Может показаться странным, что интеграл от комплексной функции получился вещественным. Однако это легко понять, если в исходном
интеграле выделить вещественную и мнимую часть. В мнимой части под интегралом окажется нечётная функция, а интеграл вычисляется в симметричных
пределах. Т.е. мнимая часть обратится в нуль, что и получилось в нашем расчёте.

Пример 4. Обход особых точек подынтегральной функции при построении контура интегрирования.
В рассмотренных примерах подынтегральная функция либо не имела особых точек, либо они были внутри контура интегрирования. Однако
бывает удобно выбрать контур так, что на него попадают особые точки функции. Такие точки приходится обходить. Обход осуществляется
по окружности малого радиуса, который в дальнейшем просто устремляется к нулю. В качестве примера вычислим интеграл .
Может показаться, что подынтегральная функция не имеет конечных особых точек, так как точка является устранимой особенностью.
Но для вычисления интеграла приходится составлять контурный интеграл от другой функции (чтобы обеспечить обращение интеграла в нуль на
замыкающей полуокружности в пределе бесконечного радиуса): . Здесь подынтегральная функция имеет полюсную особенность
в точке .

Таким образом, требуется другой контур интегрирования (см. рис. 4). Он отличается от рис. 3а только тем, что особая точка обходится по полуокружности,
радиус которой предполагается в дальнейшем устремить к нулю.
. (3)
Сразу заметим, что интеграл по большой полуокружности в пределе её бесконечно большого радиуса стремится к нулю, а внутри контура
особых точек нет, так что весь интеграл по контуру равен нулю. Далее рассмотрим первое и третье слагаемые в (3):

.
Теперь запишем интеграл по малой полуокружности, учитывая, что на ней . Также сразу будем учитывать малость радиуса полуокружности:

Не выписаны слагаемые, стремящиеся к нулю в пределе .
Собираем слагаемые в (3) — кроме относящегося к большой полуокружности слагаемого.

Как видно, обращающиеся в бесконечность при слагаемые взаимно уничтожились. Устремляя и , имеем
.
Замечание. Совершенно аналогично вычисляется, например, интеграл Дирихле (напомним, он отличается от только что рассмотренного отсутствием
квадратов в числителе и знаменателе).

Примеры вычисления определённых интегралов с помощью контурного
интегрирования в комплексной плоскости (продолжение)

Пример 5. Подынтегральная функция имеет бесчисленное множество особых точек.
Во многих случаях выбор контура осложнён тем, что у подынтегральной функции бесчисленное множество особых точек. В этом случае может
оказаться так, что сумма вычетов в действительности будет рядом, сходимость которого ещё придётся доказывать, если суммировать его
не получается (а суммирование рядов — вообще отдельная довольно сложная задача). В качестве примера вычислим интеграл .
Понятно, что часть контура — вещественная ось. На ней у функции особенностей нет. Обсудим, как замкнуть контур. Выбирать полуокружность не следует.
Дело в том, что гиперболический косинус имеет семейство простых нулей . Поэтому внутрь контура, замкнутого полуокружностью
в пределе бесконечно большого радиуса, попадёт бесконечно много особых точек. Как ещё можно замкнуть контур? Заметим, что .
Отсюда следует, что можно попробовать включить в контур интегрирования отрезок, параллельный вещественной оси. Контур замкнётся двумя
вертикальными отрезками, в пределе находящимися бесконечно далеко от мнимой оси (см. рис. 5).

На вертикальных участках контура . Гиперболический косинус с ростом аргумента (по модулю) растёт экспоненциально, поэтому
в пределе интегралы по вертикальным участкам стремятся к нулю.

Итак, в пределе
.
С другой стороны, внутри контура интегрирования находятся две особые точки подынтегральной функции. Вычеты в них
,
.
Следовательно,
.

Пример 6. Подынтегральная функция определённого и контурного интегралов различны.
Существует очень важный случай вычисления определённых интегралов методом контурного интегрирования. До сих пор подынтегральная
функция контурного интеграла либо просто совпадала с подынтегральной функцией определённого интеграла, либо переходила в неё отделением
вещественной или мнимой части. Но не всегда всё оказывается так просто. Вычислим интеграл .
В смысле выбора контура особой проблемы нет. Хотя у функции под интегралом бесконечно много простых полюсов , мы уже знаем
по опыту предыдущего примера, что нужен прямоугольный контур, так как . Единственное отличие от примера 5 заключается в том,
что на прямую попадает полюс подынтегральной функции , который нужно обойти. Поэтому выбираем изображённый
на рис. 6 контур.

Рассмотрим контурный интеграл . Мы не станем расписывать его на каждом участке контура, ограничившись горизонтальными
участками. Интеграл по вещественной оси в пределе стремится к искомому. Запишем интегралы по остальным участкам:
.
В пределе и первые два интеграла дадут , потом они войдут в контурный интеграл в сумме
с искомым, который отличается знаком. В результате из контурного интеграла искомый определённый интеграл выпадет. Это означает, что
подынтегральная функция была выбрана неверно. Рассмотрим другой интеграл: . Контур оставляем прежним.

Для начала снова рассмотрим интегралы по горизонтальным участкам. Интеграл вдоль вещественной оси перейдёт в .
Этот интеграл равен нулю как интеграл нечётной функции в симметричных пределах.

В пределе и первые две скобки обратятся в нуль, снова образовав интегралы от нечётных функций
в симметричных пределах. А вот последняя скобка с точностью до множителя даст искомый интеграл. Имеет смысл продолжать вычисление.
Аналогично примеру 5 к нулю стремятся интегралы по вертикальным участкам контура при . Остаётся найти интеграл
по полуокружности, где . Как в примере 4, вычисляем интеграл, учитывая малость :
.
Итак, у нас есть всё, чтобы записать в пределе и контурный интеграл:

А с другой стороны, внутри контура интегрирования оказался полюс подынтегральной функции , причём
.
Таким образом,
.

Пример 7. Интеграл от функции с логарифмической особенностью.
Обратимся к многозначным функциям и начнём с логарифма под интегралом. Вычислим интеграл .
У логарифма имеется точка ветвления, которую нужно обязательно обойти. В контур обязательно войдёт полуось . Как замкнуть контур?
Заметим, что на половине вещественной оси знаменатель имеет тот же вид, что и на полуоси .
Поэтому контур выберем так, как показано на рис. 7.

Начнём с интегралов по прямолинейным участкам контура:

Следует обратить внимание, что на участке от до переменная интегрирования записана как .
Нужно понимать, что записать было бы ошибкой. При обходе контура по большой полуокружности аргумент именно увеличивается
на величину .
На участке контура подынтегральная функция ведёт себя как при . Следовательно,
интеграл по большой полуокружности в пределе её бесконечного радиуса стремится к нулю.
Аналогично на малой полуокружности подынтегральная функция ведёт себя как при . Итак, в пределе и

С другой стороны, внутри контура интегрирования находится особая точка , причём
.
Итак,
.
Отделяем вещественную часть:
.
Замечание. Отделяя мнимую часть, мы получили бы значение ещё одного интеграла.

Пример 8. Интеграл от функции с логарифмической особенностью: снова изменение подынтегральной функции.
Ещё один пример, когда подынтегральные функции определённого и контурного интегралов различны. Вычислим интеграл .
Контур можно использовать всё тот же, что и в примере 7: структура интеграла это допускает. Однако на этот раз логарифм умножается на нечётную
функцию. В результате при вычислении интеграла вклады горизонтальных участков контура компенсируют друг друга.
Искомый интеграл сокращается — так же, как это произошло в примере 6.
Мы не будем убеждаться в сокращении искомого интеграла в рассмотренной схеме вычислений, а сразу предложим ведущий к ответу путь.
Вычислять следует контурный интеграл по тому же контуру (см. рис. 8).

Аналогично примеру 7 легко показать, что интегралы по полуокружностям в пределе и стремятся к нулю.
Рассмотрим интегралы по горизонтальным участкам:

Как видно, ненужный интеграл в контурный интеграл не войдёт. В пределе и
.
С другой стороны, внутри контура находится особая точка , причём
.
Следовательно,
.
Отделяя мнимую часть, находим:
.
Примеры вычисления определённых интегралов с помощью контурного
интегрирования в комплексной плоскости (окончание)

Пример 9. Интеграл от функции со степенной особенностью. Разрезы на комплексной плоскости.
Иногда подынтегральная функция такова, что выбор контура осложняется сильной ограниченностью вариантов элементов контура, по которым
интеграл удастся вычислить. На примере интеграла поясним суть проблемы и укажем, как поступать в этом случае.
Вычислять будем контурный интеграл . Выберем контур интегрирования. Естественно, в него войдёт полуось .
Только точку нужно обойти: степенная функция многозначна, а точка является точкой ветвления.
Как можно замкнуть контур? Оказывается, оптимальный вариант — контур, изображённый на рис. 9.

Поясним рис. 9. Подынтегральная функция многозначна, так как в ней присутствует степенная функция.
Вообще говоря, логарифмическая функция в предыдущих примерах тоже была многозначна, но к каким-то специфическим следствиям это
не приводило. Отличие в выбранном контуре. В данном примере при обходе контура мы обходим точку ветвления, вследствие чего может
произойти переход к другой ветви многозначной функции. Чтобы этого избежать, вводится разрез (отмечен красной прямой).
В результате когда мы проходим отрезок слева направо, мы двигаемся по верхнему берегу разреза. Когда мы обошли точку
ветвления по участку и двигаемся по тому же отрезку, но в обратном направлении, то мы уже двигаемся по нижнему берегу разреза.
Формально это означает, что необходимо учитывать увеличение аргумента на при обходе точки ветвления.
Переходим к вычислению. Сразу заметим, что интегралы по дугам окружностей в пределе и стремятся к нулю — это легко показать.
Аккуратно проведём интегрирование по берегам разреза:
.
В пределе и получим с точностью до множителя искомый интеграл.
С другой стороны внутри контура интегрирования попал простой полюс подынтегральной функции , причём
.
Таким образом,
,
.

Пример 10. Отслеживание изменения аргумента при обходе точек ветвления.
При вычислении несобственных интегралов второго рода обычно требуется обходить в комплексной плоскости точки ветвления подынтегральной
функции. При этом важно отследить, как меняется аргумент при обходе точки ветвления. Мы продемонстрируем это на простом примере, чтобы
технические детали не заслонили основной идеи. Вычислим интеграл . Очевидно, этот интеграл равен .
Вычисление почти устное: применима формула Ньютона-Лейбница.
Теперь вычислим этот интеграл, рассматривая контурный интеграл . Подынтегральная функция имеет две точки ветвления .
Для выделения ветвей проводим разрез по отрезку , сами точки ветвления обходим — в результате получается изображённый
на рис. 10 контур интегрирования.

Интегралы по малым окружностям в пределе их бесконечно малого радиуса стремятся к нулю. Дальше нужно проводить интегрирование по берегам
разреза. Здесь следует сделать замечание. Конечно, мы обошли особые точки, но при обходе точек ветвления нужно отслеживать, с какой именно
ветвью многозначной функции мы имеем дело. Принципиальную роль здесь играет аргумент участвующих в расчёте величин. В частности, важно знать,
как меняется аргумент всей подынтегральной функции при обходе контура. Прежде всего следует зафиксировать ветвь многозначной функции. Потребуем,
чтобы на верхнем берегу разреза подынтегральная функция была равна . Перепишем рассматриваемую комплексную функцию
в виде . Посмотрим, что происходит с при обходе точки по участку . Заметим, что при этом приращение
аргумента (точка не обходилась) и (произошёл обход точки в отрицательном направлении).
Таким образом, . Следовательно, при переходе по участку контура с верхнего берега
разреза на нижний функция приобретёт множитель , т.е. в пределе бесконечно малого радиуса участков и
.
С другой стороны этот контурный интеграл равен . Чтобы найти вычет, разложим функцию в ряд Лорана в окрестности
бесконечно удалённой точки:
.
Вычет — взятый с противоположным знаком коэффициент при минус первой степени, т.е. . Чему равен корень ?
Это зависит от выбранной ветви функции . Может быть или . Чтобы сделать выбор, рассмотрим обход точки ,
но не до нижнего берега разреза, а до вещественной оси (см. рис. 11). Тогда .
При этом . До обхода точки , а при обходе приращение
аргумента составило . Поэтому , т.е. . Таким образом, , а потому
.

Пример 11. Интеграл от функции с точками ветвления.
Покажем, как вычисляются более сложные интегралы от функций, имеющих точки ветвления. Расчёт по сути аналогичен показанному в примере 10,
поэтому комментарии будут менее подробные. Вычислим интеграл .
Контур интегрирования мало отличается от использованного в предыдущем примере. Теперь точки ветвления .
Они по-прежнему обходятся по малым окружностям, между точками ветвления проведён разрез.

При обходе точки ветвления
.
Снова интегралы по малым окружностям в пределе их бесконечно малого радиуса стремятся к нулю, поэтому в этом пределе
.
С другой стороны этот контурный интеграл равен . Как и в примере 10, разложим функцию в ряд Лорана в окрестности
бесконечно удалённой точки:

.
Выделяя минус первую степень и находим . Значение корня из минус единицы снова
определим, рассматривая обход точки по дуге окружности до вещественной оси. При этом приращение аргумента функции
под интегралом составит , но
,
а значит .
Таким образом,
.
с точками ветвления классно.
а как считать приращение аргумента ?
это для меня всегда было загадкой
panicdoctor, по поводу аргумента. Для начала напомню, что это вообще такое. Если есть комплексное число
, то его аргументом (а точнее, главным значением аргумента) называется число

В геометрической интерпретации комплексное число изображается точкой на плоскости, абсцисса которой — вещественная
часть числа, ордината — мнимая часть числа. С другой стороны комплексное число характеризуется модулем и аргументом.
Модуль в геометрической интерпретации — расстояние от точки, изображающей число, до начала координат, а аргумент — угол,
который составляет радиус-вектор точки, изображающей число, с осью абсцисс. Угол отсчитывается от оси абсцисс против часовой
стрелки (см. рис. 13).

Теперь к вопросу о том, как определяется изменение аргумента. Рассмотрим точку . Предположим, что мы переходим
в точку по дуге окружности в комплексной плоскости (см. рис. 14). При этом радиус-вектор точки
совершает поворот на угол . Это и есть изменение аргумента. Если переход совершается по дуге окружности ,
то радиус-вектор точки поворачивается тоже на угол , но в направлении, противоположному тому, в котором угол
отсчитывается. Поэтому изменение аргумента составит .
Если же мы переходим, например, в точку (см. рис. 15), то при переходе по пути изменение аргумента будет нулевым,
так как в результате радиус-вектор точки вернётся в прежнее положение, но угол, который он образует с осью абсцисс, в процессе
перехода сначала возрастает, а потом убывает.
Если же переход осуществляется по пути , то аргумент получает приращение .

В примерах 10, 11 требовалось находить изменение аргумента величин , и т.п.
В этих случаях радиус-вектор следует проводить из точек , соответственно, так как имеет
значение обход именно вокруг этих точек. Это следует и из формального определения аргумента: вычисление аргумента
существенно зависит от знака вещественной части. При нахождении аргумента некоторой функции от следует смотреть,
где происходит обращение в нуль вещественной части этой функции.
Schufter, большое спасибо за истолкование )

Поделиться этой страницей

Источник

Рассмотрим
несколько примеров на применение вычетов
к вычислению интегралов по замкнутому
контуру, используя основную теорему о
вычетах(формула 4.4).

Алгоритм
вычисления интегралов

с помощью
вычетов

1.
Найти особые точки функции f(z).

2.
Определить, какие из этих точек расположены
в области ограниченной контуром C.
Для этого
достаточно сделать чертёж: изобразить
контур C
и отметить
особые точки.

3.
Вычислить вычеты в тех особых точках,
которые расположены в области D.

4.
Записать результат по формуле ( 4.4):

Пример 1.

Вычислить
интеграл

Записываем решение по алгоритму.

К
онечными
особыми точками функции

являются нули знаменателя,

,
т.е.

, k = 0,1,2,3. Заметим, что
все точки – простые нули знаменателя,
следовательно, простые полюсы f(z).
Контуром интегрирования является
окружность

, а точки

расположены в вершинах квадрата,
вписанного в окружность

(рис.4.5). Поэтому в область, ограниченную
контуром, попадают точки

и

. Заметим, что

.

3. Находим вычеты в точках по формуле
(4.8):

4. Записываем ответ:

Пример 2.

Вычислить интегралы:

a)

;
б)

.

Единственный конечной особой точкой
каждой из подынтегральных функций
является

—
существенно особая точка. В обоих случаях
она принадлежит области, ограниченной
контуром интегрирования. Вычеты находим,
раскладывая функции по степеням z
(см примеры 2 и 3 §1).

Получаем

Записываем ответ: а)

; б)

.

Пример 3.

Вычислить интегралы:

а)
; б)

.

а) Воспользуемся алгоритмом.

1. Находим конечные особые точки функции

—
корни уравнения
,
следовательно,

,

2. В область

входят точки

,
так как

и

.
Другие точки не принадлежат кругу
,
так как для них

.

3. Точка

— устранимая особая точка функции, так
как, применив

,

;

поэтому

.
Точка z=-1 является полюсом
первого порядка

,
поскольку она − простой нуль знаменателя,
а числитель при этом не обращается в
нуль, следовательно, функция записывается
в виде

.
Вычет вычисляем по формуле (4.8) :

4.Запишем ответ:

б) Воспользуемся алгоритмом.

1. Особыми точками функции являются нули
знаменателя — корни уравнения

или

,откуда

,

2. Из всех найденных корней кругу

принадлежит только одна точка

.

3,4. Находим вычет в точке

— простом полюсе

Записываем ответ:
.

Пример 4.

Вычислить интегралы:

а)

; б)

.

а) Особыми точками функции

являются простые полюсы

и

,

Точка

не принадлежит кругу

,
точки

расположены на окружности

,следовательно,
принадлежат кругу

.
Применяя формулу ( 4.4), можно найти вычеты
в этих точках, получив ответ:

Чтобы не вычислять вычеты в 15 особых
точках

,
применим обобщенную теорему о вычетах
(формулу(4.5)). В данном случае она имеет
вид

и, следовательно,

Для

— простого полюса

вычет находим по формуле (4.8):

Точка

—
устранимая особая точка для

и

.
Вычет вычисляем по формуле (4.10):

Получаем ответ:
.

б) Особыми точками функции

являются точки

— простой полюс и точка

—
существенно особая точка. Обе точки
принадлежат кругу

Вычет в точке

находим по формуле (4.8):

Для нахождения вычета в существенно
особой точке

нужно найти коэффициент c_-1в разложении функции

в ряд Лорана по степеням

.
Для этого записываем разложения в ряд
Лорана функций

и

,
перемножаем ряды и находим c_-1— коэффициент при степени

.

Заметим, вычет в существенно особой
точке

можно вычислить, используя формулу
(4.5).Из равенства

следует

.

Поэтому

Пример 5.

Вычислить интеграл

,где
С-граница круга единичного радиуса
с центром в точке

:

а)

б)

.

Особыми точками подынтегральной функции
являются

— полюс первого порядка,

− существенно особая точка и

— устранимая особая точка(см. пример
4.6).

а) В круг

входит точка

.
Находим вычет по формуле (4.8):

Получаем ответ:

.

б) В круг

входят две точки:

— существенно особая точка,

− устранимая особая точка. Поэтому

или, применяя формулу (4.5) (чтобы избежать
вычисления вычета в существенно особой
точке), получаем

Так как

,
находим

по формуле (4.8):

Получаем ответ:

.

ЛИТЕРАТУРА

1. Лаврентьв М.А.
, Шабат Б.В. Методы теории функций
комплексного переменного. «Наука»,
Москва, I 965.

2.
Маркушевич А.И. Краткий куре теории
аналитических функций. «Наука», Москва,
I 966.

3.
Свешников А.Г. Тихонов А.В. Теория функций
комплексной переменной. «Наука», Москва,
I 970.

4.
Фукс Б.А.‚ Шабат Б.В. Функции комплексного
переменного и некоторые их приложения.
Физматгиз. Москва, I 959.

5.
Конторович М.И. Операционное исчисление
и процессы в электрических цепях.
«Наука», Москва, I 964.

Рассмотрено и рекомендовано к рассмотрению
учебно-методического совета КИ (ф)
МГОУ

на заседании кафедры

Высшей и прикладной математики

КИ (ф) МГОУ «22» февраля 2012
г.

протокол № 7

Рекомендовано
к печати решением

учебно-методического
совета

КИ
(ф) МГОУ от
«___» _____________2012
г.

протокол
№ ___

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение. Если функция определена на кусочно-гладкой кривой L и точки этой кривой разбивают ее на n элементарных дуг, в каждой из которых выбрана точка то , называется интегралом от f(z) по кривой L и обозначается или, в случае замкнутого контура L .

Если функция непрерывна на L, то интеграл существует (его часто называют контурным):

, (2.34)

где

являются криволинейными интегралами от функций двух действительных переменных.

Если кривая L задана параметрическими уравнениями:

и каждая из этих функций гладкая, то

. (2.35)

Известно, что вместо двух вещественных параметрических уравнений линии L можно ввести одно эквивалентное им комплексно-параметрическое уравнение

тогда уравнение (2.35) можно переписать так:

. (2.36)

Формула (2.36) удобна для вычисления контурных интегралов.

Теорема 1 (основная теорема Коши). Если функция f(z) аналитична в односвязной области, то для любого кусочно-гладкого замкнутого контура L, лежащего в этой области,

Следствие. Если функция f(z) аналитична в односвязной замкнутой области, ограниченной кривой L, то

Заметим, что из теоремы Коши следует: если функция f(z) аналитична в односвязной области D, то для любой незамкнутой кривой L, принадлежащей D, интеграл от f(x) по L зависит только от начальной точки z₀ и конечной точки z, т.е. от формы кривой (пути) L не зависит. При этом:

, (2.37)

где F(z) – одна из первообразных функций для f(z), т.е. F’(z) = f(z). Формула (2.37) называется формулой Ньютона-Лейбница.

Теорема 2. Если функция f(z) аналитична в замкнутой области (односвязной или многосвязной) и L – граница D, то для любой точки z₀, лежащей внутри этой области, справедливы следующие формулы:

; (2.38)

(2.39)

Интеграл в правой части формулы (2.39) называется интегралом Коши для функции f(z), а сама эта формула носит название интегральной формулы Коши.

Формулу (2.39) часто называют интегральной формулой Коши для n-й производной функции f(z), и она выражает тот факт, что аналитическая функция, заданная в замкнутой области , дифференцируема сколько угодно раз в каждой точке z области D (следовательно, производные f’(z), f’’(z),,… аналитичны в точке z).

Отметим, что формула (2.39) получается из интегральной формулы Коши (2.38) в результате последовательного дифференцирования n раз по z₀ под знаком интеграла.

Пример 1

Вычислить контурный интеграл где L – прямолинейный отрезок, соединяющий точку z = 0 с точкой z = 3+7i.

Решение

1) Сделаем схематический рисунок пути (контура) интегрирования (рис. 2.3).

2) Составим параметрические уравнения или комплексно-параметрическое уравнение пути (контура) интегрирования. Если путь интегрирования состоит из прямолинейных участков, то целесообразно использовать формулу для прямой, проходящей через две заданные точки:

Из условия z = 0, следует, что

;

из условия z = 3+7i, следует, что

Получаем:

отсюда

3) Установим, как изменяется параметр t при движении от точки z = 0 до точки z = 3 + 7i.

При z = 0 у нас х = 0 и у = 0, а значит, из параметрических уравнений t = 0; при z = 3 + 7i имеем x = 3 и у = 7, тогда из тех же уравнений находим t = 1.

Таким образом, . Используем формулу (2.36):

Ответ:

Замечание.

Если путь интегрирования состоит из двух отрезков, то составляются параметрические уравнения для каждого участка отдельно и находятся два интеграла.

Пример 2

Построить область, заданную на комплексной плоскости

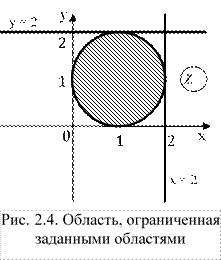
Решение

Запишем область в другом виде с учетом, что получим:

Это область, ограниченная окружностью с центром в точке (1, 1) и радиусом 1.

Ограничение запишем в виде:

Ограничение имеет вид:

Получили область, ограниченную графиками:

;

Изобразим область на графике (рис. 2.4). Заданная область заштрихована.

Пример 4

Найти интеграл от функции комплексного переменного, используя основную теорему Коши:

Решение

1) Построим область интегрирования:

получим

;

, .

Получили уравнение окружности с центром в точке О и радиусом (рис. 2.5).

2) Найдем точки и изобразим их на рисунке 2.5.

Из формулы (2.38) следует, что

Получаем, что . Точка не попадает в область интегрирования, следовательно,

1) Определяем интеграл, используя формулу (2.38):

Получаем:

;

Ответ:

Пример 5

Найти интеграл от функции комплексного переменного используя основную теорему Коши: .

Решение

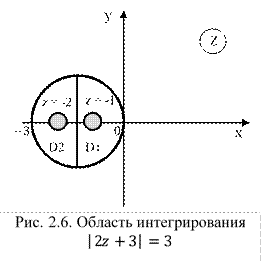
1) Построим область интегрирования:

Получим:

;

Получили уравнение окружности с центром в точке О и радиусом (рис. 2.6).

2) Найдем точки и изобразим их на рисунке 2.6.

Из формулы (2.38) следует, что

Обе точки лежат в области интегрирования, следовательно, разбиваем область интегрирования на две замкнутые области D1 и D2. Интеграл разбиваем на два: