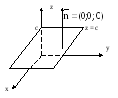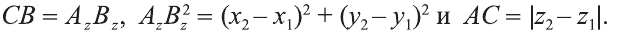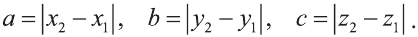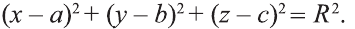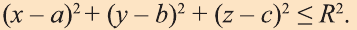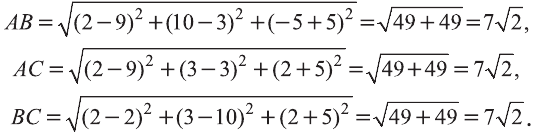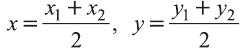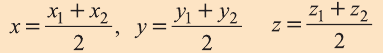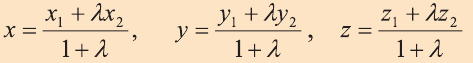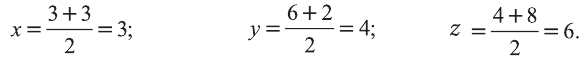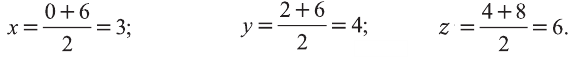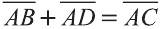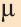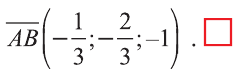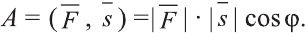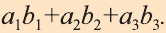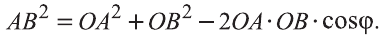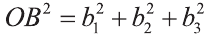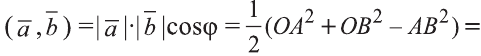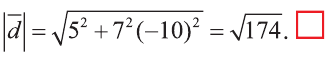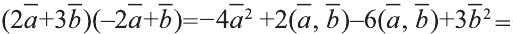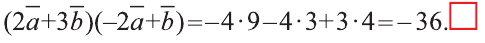Как найти координатную плоскость оху

Лекции
по алгебре и геометрии. Семестр 1.

Лекция
12. Общее и нормированное уравнение
плоскости и прямой на плоскости.

Краткое содержание: векторное уравнение
плоскости и прямой на плоскости, общее
уравнение плоскости и прямой на плоскости,
неполные уравнения прямой на плоскости
и неполные уравнения плоскости,
нормированные уравнения прямой на
плоскости и плоскости.

Глава
12. Общее и нормированное уравнение
плоскости и прямой на плоскости.

п.1.
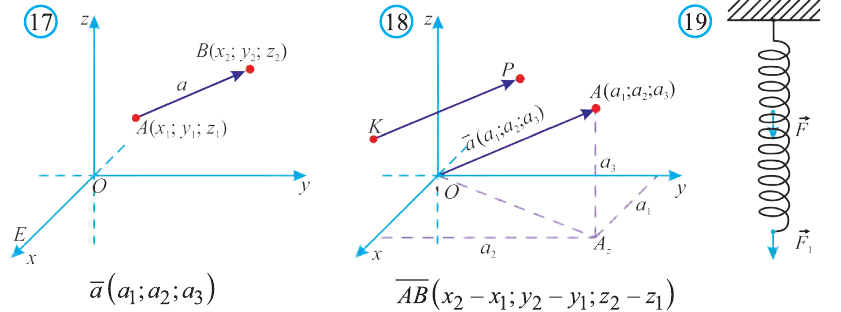
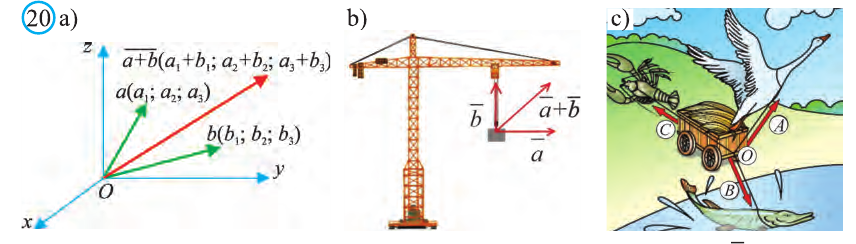
Векторное уравнение плоскости и прямой
на плоскости.

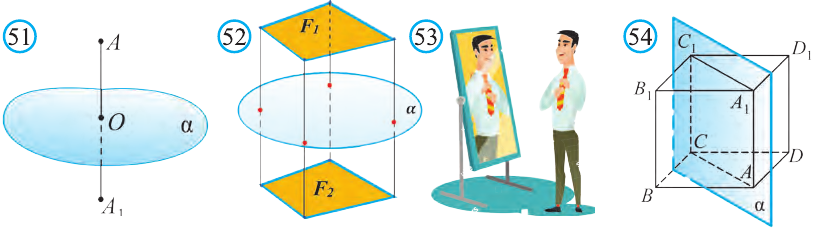
Определение.
Любой ненулевой вектор, перпендикулярный
плоскости (прямой на плоскости) называется
нормальным вектором этой плоскости
(прямой на плоскости).

Теорема.
Пусть

– радиус-вектор текущей точки М плоскости
(прямой на плоскости),

– радиус- вектор какой-нибудь фиксированной
точки

плоскости (прямой на плоскости),

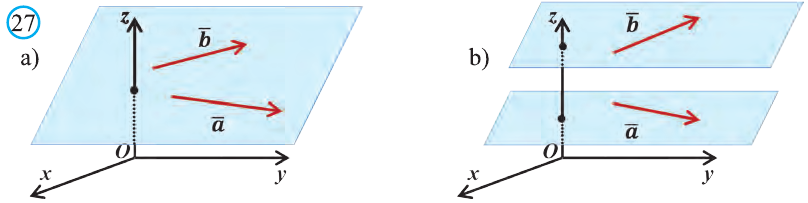
– нормальный вектор плоскости (прямой
на плоскости). Тогда уравнение

(1)

является
векторным уравнением плоскости (прямой
на плоскости).

Доказательство.
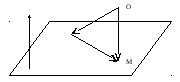
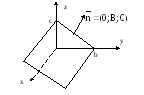
Изобразим на рисунке прямую L,
ее нормальный вектор

и радиус-векторы

и
.

рис.1.

По
правилу треугольника сложения векторов
имеем:

и точка
,
откуда и следует доказываемое уравнение
(1).

Доказательство
для случая плоскости точно такое же,
см. рис.2:

рис.2.

Теорема
доказана.

п.2.
Общее уравнение плоскости и прямой на
плоскости.

Теорема.
Для любой прямой на координатной
плоскости Оху ее уравнение имеет вид

,
(2)

где
,

– нормальный вектор прямой. Обратно,
для любых
,
где А и В одновременно не равны нулю,
уравнение (2) является уравнением прямой,
лежащей на координатной плоскости Оху.

Доказательство.
1) Пусть L произвольная
прямая на координатной плоскости Оху
и пусть точка

ее произвольная фиксированная точка,
М(х, у) – ее текущая точка,

– ее произвольный нормальный вектор.
Тогда уравнение (1) является векторным
уравнением этой прямой, где
,
.

Расписывая скалярное
произведение в координатной форме,
получаем
.
Раскрывая скобки и группируя, получаем

.

Обозначая
через
,
получаем отсюда равенство (2), которое
и будет уравнением данной прямой.

2)
Пусть дано уравнение

,
(2)

где
А, В и С – произвольные действительные
числа и пара (А, В) – не нулевая. Пусть
для определенности
.
Тогда
,
откуда мы видим, что любая пара
,
где

является решением уравнения (2) и,
следовательно, это уравнение имеет
бесконечное множество решений.

Пусть

и

– два различных произвольных фиксированных
решений уравнения (2), и (х, у) произвольное
его решение т.е.

,
,
.

Отсюда

(3)

и
подставляя в оставшиеся два равенства,
получаем:

и
.
(4)

На
координатной плоскости Оху каждому
решению уравнения (2) соответствует
точка. Пусть,

,
М(х, у) – точки, соответствующие выбранным
решениям. Тогда равенства (4) в векторной
форме имеют вид

,
,
(5)

т.е.

и
,
откуда следует, что

,
(6)

что,
в свою очередь, означает, что для любой
точки М, координаты которой удовлетворяют
уравнению (2), точки М,

и

лежат на одной прямой L,
проходящей через фиксированные точки

и
.

С
другой стороны, если точка М(х, у) лежит
на этой прямой L, то верно
(6), (5) и (4). Подставляя (3) во второе из
равенств (4), получаем (2).

Таким образом,
уравнению (2) удовлетворяют координаты
тех и только тех точек, которые лежат
на прямой, ч.т.д.

Теорема
доказана.

Определение.
Уравнение прямой вида

называется
уравнением прямой, проходящей через
заданную точку

и с заданным нормальным вектором
.

Теорема.
Уравнение любой плоскости в координатном
пространстве Охуz имеет
вид

,
(7)

где
,

– нормальный вектор плоскости. Обратно,
пусть
–
произвольные действительные числа,
причем числа А, В и С одновременно не
равны нулю. Тогда уравнение (7)

является
уравнением плоскости в координатном
пространстве Охуz.

Доказательство
аналогично доказательству предыдущей
теоремы, хотя и технически немножко
сложнее. Первая часть доказательства
практически такая же, а во второй части
нужно брать три фиксированных решения
(соответственно три точки пространства)
и одно произвольное уравнения (7) и
доказать, что любое решение уравнения
(7), отождествленное с точкой пространства,
лежит в той же плоскости, которая проходит
через выбранные три точки и, что любая
точка пространства лежащая на этой
плоскости удовлетворяет уравнению (7).

Определение.
Уравнение

называется общим уравнением прямой на
координатной плоскости Оху. Уравнение

называется общим уравнением плоскости.
Действительные числа А, В, С, D
называются коэффициентами соответствующих
уравнений.

п.3.
Уравнение прямой в отрезках.

Пусть ни один из
коэффициентов А, В, С общего уравнения
прямой

,

не
равен нулю. Перенесем свободный член С
в правую часть уравнения и разделим обе
части уравнения на (– С):

.

Обозначим
.
Тогда последнее уравнение можно записать
в виде:

.
(8)

Определение.
Уравнение вида (8) называется уравнением
прямой в отрезках.

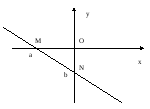
Для
построения прямой достаточно взять две
точки на этой прямой. Для построения
прямой в отрезках удобно найти ее точки
пересечения с координатными осями:

М(а,
0) – точка пересечения прямой (8) с осью
Ох и

N(0,
b) – точка пересечения
прямой (8) с осью Оу.

рис.3.

Говорят,
что прямая отсекает от координатных
осей отрезки ОМ и ОN
величина которых равна числам а и b
соответственно.

Замечание.
Под величиной отрезка ОА здесь понимается
не его длина
,
а координата точки М, т.е. число а.
Аналогично, величина отрезка ОN
равна числу b.

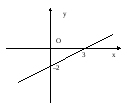
Пример.
Построить прямую
.

Решение.
Запишем данное уравнение прямой в виде
уравнения прямой в отрезках. Для этого
перенесем коэффициент – 6 в правую часть
уравнения:

и разделим обе
части уравнения на 6:

.
После сокращения получаем:

.

Данная
прямая отсекает от оси Ох отрезок
величина которого равна 3, а от оси Оу –
отрезок, величина которого равна –2.

Откладываем на
оси Ох точку с координатой 3, а на оси Оу
откладываем точку с координатой –2 и
проводим через эти точки прямую:

рис.4.

п.4.
Неполные уравнения прямой на плоскости.

Определение.
Уравнение

(2)

называется неполным
уравнением прямой на плоскости, если
хотя бы один из его коэффициентов А, В,
С равен нулю.

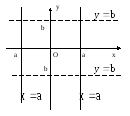
Если
коэффициент
,
,
то из уравнения (2) следует
.
Это уравнение прямой, параллельной оси
Оу, отсекающей от оси Ох отрезок величиной
а.

Если
коэффициент
,

то из уравнения (2) следует
.
Это уравнение прямой, параллельной оси
Ох, отсекающей от оси Оу отрезок величиной
b.

рис.5.

Если
,
то уравнение (2) принимает вид

.
(9)

Ясно,
что эта прямая проходит через начало
координат.

Если
в уравнении (9) коэффициент
,
то отсюда получаем
.
Обозначив через
,
получаем уравнение, которое носит
название уравнения прямой с угловым
коэффициентом
,
которое изучалось в школьном курсе
алгебры.

Если
в уравнении (9)
,
то

и, сокращая на А, получаем уравнение оси
Оу:
.

Если
в уравнении (9)
,
то

и, сокращая на В, получаем уравнение оси
Ох:
.

Подведем итог
исследования общего уравнения прямой

(2)

1)
Если
,
то уравнение (2) может быть записано в
виде уравнения прямой в отрезках:

–
прямая, отсекающая
от осей координат отрезки величиной а
и b соответственно.

2)
Если
,
то уравнение может быть записано в виде:

–
прямая параллельная
оси Ох и отсекающая от оси Оу отрезок
величины b.

3)
Если
,
то уравнение может быть записано в виде:

–
прямая параллельная
оси Оу и отсекающая от оси Ох отрезок
величины а.

4)
Если
,
то уравнение прямой имеет вид

–
прямая совпадает
с осью Ох.

5)
Если
,
то уравнение прямой имеет вид

–
прямая совпадает
с осью Оу.

6)
Если
,
то уравнение может быть записано в виде:

– уравнение прямой с угловым коэффициентом.

п.5.
Уравнение плоскости в отрезках. Неполные
уравнения плоскости.

Исследование
общего уравнения плоскости

,
(7)

где

– координаты ее нормального вектора,
производится аналогично исследованию
общего уравнения прямой на плоскости.
Приведем ниже все случаи.

Если
,
то уравнение (7) может быть записано в
виде уравнения плоскости в отрезках:

(10)

–
плоскость, отсекающая
от осей координат отрезки величиной а,
b и с соответственно, где
обозначено

.

рис.6.

Определение.
Уравнение

называется
неполным уравнением плоскости, если
хотя бы один из его коэффициентов А, В,
С, D равен нулю.

Если
,
то уравнение (7) имеет вид

.
(11)

В
координатной плоскости Оуz
это уравнение есть уравнение прямой, а
так как
,
то данная плоскость параллельна оси
Ох. Уравнение (11) может быть записано в
виде

(12)

или

– уравнение плоскости параллельной
координатной плоскости Охz
и отсекающей от оси Оу отрезок величины
b,

или

– уравнение плоскости параллельной
координатной плоскости Оху и отсекающей
от оси Оz отрезок величины
с.

рис.7.

рис.8.

рис.9.

Если
,
то уравнение (6) имеет вид

.
(13)

Это
уравнение прямой в координатной плоскости
Оуz, проходящая через
начало координат и в то же время уравнение
плоскости, содержащей ось Ох.

рис.10.

Если
в уравнении (13)
,
то получаем

–
уравнение
координатной плоскости Оху.

Если
в уравнении (13)
,
то получаем

–
уравнение
координатной плоскости Охz.

Ситуации, когда

или

исследуются аналогично.

Подведем
итог исследованию общего уравнения
плоскости

.
(7)

1)
Если
,
то можно уравнение (7) записать в виде
уравнения в отрезках

,

где
а, b, с – величины отсекаемых
плоскостью от координатных осей отрезков.

2)
Если
,
но один из коэффициентов А, В, С равен
нулю, то получаем уравнение плоскости
в виде

или

или

–
плоскость
параллельная оси Оz или
Оу или Ох соответственно.

3)
Если
,
но два из коэффициентов А, В, С равны
нулю, то получаем уравнение плоскости
в виде

или

или

–
соответственно
плоскость параллельна координатной
плоскости Оуz или Охz
или Оху.

4)
Если
,
то уравнение (7) принимает вид

–
плоскость содержит
начало координат.

5)
Если

и один из коэффициентов А, В, С равен
нулю, то получаем уравнение плоскости
в виде

или

или

–
плоскость содержит
соответственно ось Ох или ось Оу или
ось Оz.

6)
Если

и два из коэффициентов А, В, С равны нулю,
то получаем уравнение плоскости в виде

или

или

– уравнение соответственно координатных
плоскостей Оуz или Охz
или Оху.

п.6.
Нормированное уравнение плоскости и
прямой на плоскости.

Пусть

(1)

–
векторное уравнение
плоскости или прямой на плоскости, где

– нормальный вектор плоскости (прямой),

– радиус-вектор фиксированной точки
плоскости (прямой),

– радиус-вектор текущей точки плоскости
(прямой).

Заметим, что в
уравнении (1) длина нормального вектора
не играет никакой роли. Выберем в
уравнении (1) в качестве нормального
вектора

нормальный вектор единичной длины
,
а направление нормального вектора
выберем такое, чтобы угол между вектором

и

был острый. Смотри следующие рисунки.

рис.11.

рис.12.

Иначе, направление
вектора

должно быть от начала координат к
плоскости (прямой). Раскроем в уравнении
(1) скобки

и
разделим обе части уравнения на
,
если скалярное произведение

или на
,
если
.
Получим

,
(14)

где
.

Обозначим

и пусть
,
.
Так как координатами единичного вектора
являются его направляющие косинусы, то
.
Подставляя в (14), получаем

.

Определение.
Уравнение вида

,
(15)

где
,

– направляющие косинусы нормального
вектора плоскости, называется нормированным
(нормальным) уравнением плоскости.

В
случае прямой на координатной плоскости
Оху имеем:
,
,

и

.

Определение.
Уравнение вида

,
(16)

где
,

– направляющие косинусы нормального
вектора прямой, называется нормированным
(нормальным) уравнением прямой на
координатной плоскости Оху.

Заметим, что в
уравнениях (15) и (16) свободный коэффициент
(– р) отрицательный, р численно равно
расстоянию от начала координат до
плоскости (прямой):

.

В
этом заключается геометрический смысл
свободного члена р в этих уравнениях.

Пример.
Записать нормированное уравнение
плоскости, если его общее уравнение
имеет вид:

и
найти расстояние от начала координат
до плоскости.

Решение. Имеем,
,
.

Так
как свободный коэффициент этого уравнения
равен положительному числу 26, то для
получения нормированного уравнения
плоскости разделим обе части общего
уравнения на число, противоположное
модулю нормального вектора:

.

Ответ:

– нормированное уравнение плоскости.
Расстояние от начала координат до
плоскости равно 2.

Аналогично
приводится к нормальному виду общее
уравнение прямой.

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

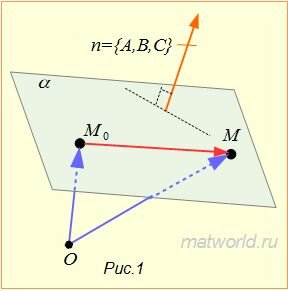
Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

которая эквивалентна уравнению (1).

Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n={A,B,C} (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n={A,B,C} и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

Если же точка M(x, y, z) не лежит на плоскости α, то векторы n={A,B,C} и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости, определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

и

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

Доказательство. Так как уравнения (4) и (5) определяют одну и ту же плоскость, то нормальные векторы n₁={A₁,B₁,С₁} и n₂={A₂,B₂, С₂} коллинеарны. Так как векторы n₁≠0, n₂≠0, то существует такое число λ, что n₂=n₁λ. Отсюда имеем: A₂=A₁λ, B₂=B₁λ, С₂=С₁λ. Докажем, что D₂=D₁λ. Очевидно, что совпадающие плоскости имеют общую точку M₀(x₀, y₀, z₀), так что

и

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным, если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным.

Рассмотрим все возможные варианты неполных уравнений плоскости:

При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n={0,B,C} лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n={A,B,C}={0,0,1}, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

или

Ответ:

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n=={2,3,1}.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

Так как плоскость имеет нормальный вектор n={A,B,C}={2,3,1}, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

или

Ответ:

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

A(x−x0)+B(y−y0)+С(z−z0)=0,

(3)

которая эквивалентна уравнению (1).

Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

A2=A1λ, B2=B1λ, C2=C1λ, D2=D1λ.

(6)

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)y₀+(C₁λ−C₂)z₀+(D₁λ−D₂)=0.

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

A(x−4)+B(y−(−1))+C(z−2)=0

(9)

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

0(x−4)+0(y−(−1))+1(z−2)=0

(9)

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

A(x−0)+B(y−0)+C(z−0)=0

(10)

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

2(x−0)+3(y−0)+1(z−0)=0

(9)

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

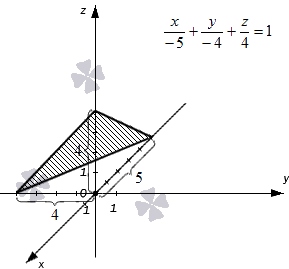
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Система координат в пространстве — определение с примерами решения

Содержание:

Система координат в пространстве

Декартова система координат в пространстве

Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

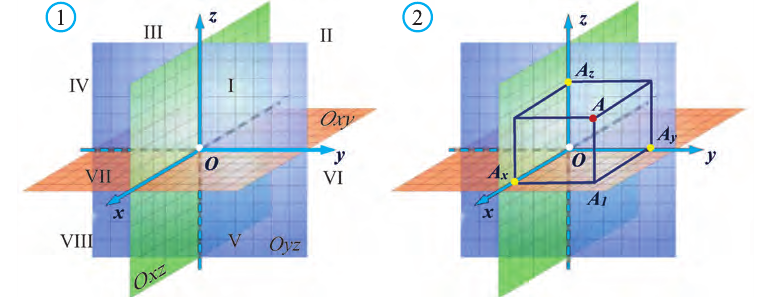
точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.

Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.

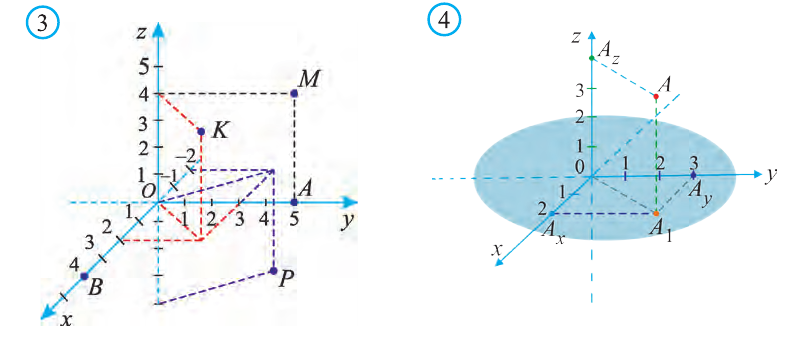
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).

Пример:

Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ 2 = АС 2 + СВ 2 .

Однако

Поэтому

2.Пусть отрезок АВ параллелен оси Оz, тогда 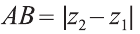и, так как

Следовательно, расстояние между двумя точками А и В:

(1)

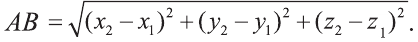
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны

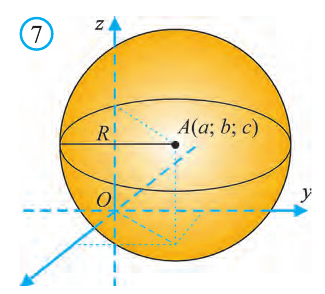
Уравнение сферы и шара

Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид:

Пример:

Найдите периметр треугольника ABC с вершинами в

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 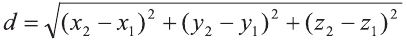расстояния между двумя точками, найдём длины сторон треугольника:

Следовательно, треугольник ABC равносторонний и его периметр .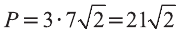

Ответ:

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).

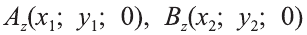
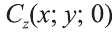
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках и . Тогда по теореме Фалеса точка С_z — середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

Аналогично, используя координаты концов A и B отрезка AB, по формулам

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

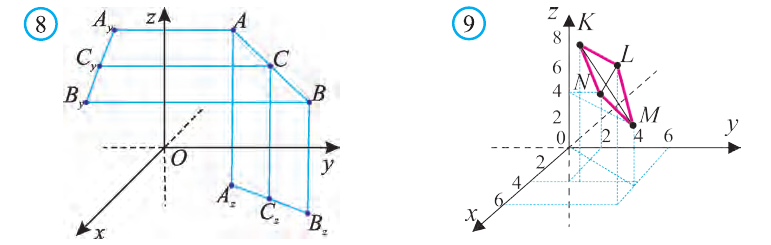
Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

Координаты середины отрезка NL:

Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

Векторы в пространстве и действия над ними

Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

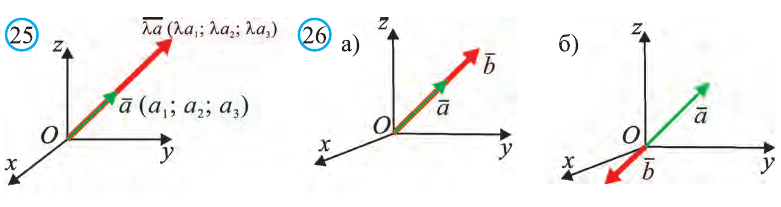
Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 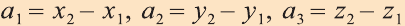, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

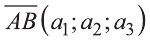
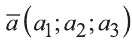
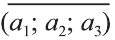
Hа основании этого вектор можно обозначить как или или кратко (рис. 18).

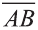
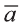
Вектор можно записать и без координат (или ). В этой записи

на первом месте начало вектора, а на втором — конец.

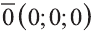
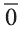
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают или , направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

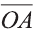
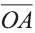
координатами вектора : (а₁; а₂; а₃).

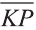
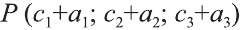
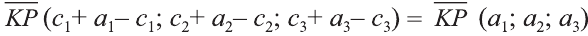
Однако вектор в пространстве с началом в точке К(с₁; с₂; с₃) и концом в точке будет иметь те же координаты: .

Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора 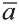записывают

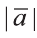
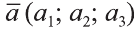
так. Длина вектора , заданного координатами,

вычисляется по формуле .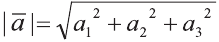

Пример:

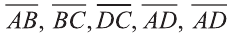
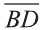
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов и равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

Следовательно, .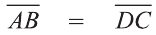

Докажите самостоятельно, что

Действия над векторами в пространстве

Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

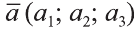
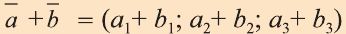
Суммой векторов и (b₁; b₂; b₃); называют вектор (рис. 20).

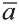
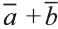
Пусть кран на рисунке 20.b движется вдоль вектора , а груз относительно крана вдоль вектора . В результате груз движется вдоль вектора . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

Свойства суммы векторов

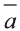
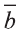
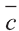
Для любых векторов , и имеют место следующие свойства:

a) — переместительный закон сложения векторов;

b) — распределительный закон сложения.

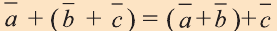
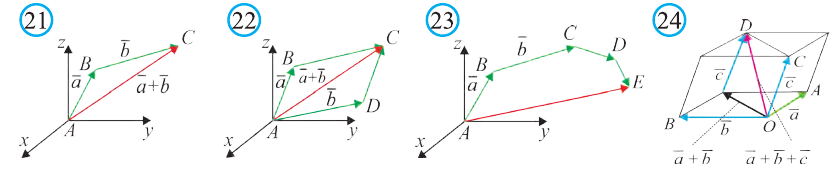
Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):

Правило параллелограмма сложения векторов

Если АВСD — параллелограмм (рис. 22), то

Правило многоугольника сложения векторов

Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то

Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

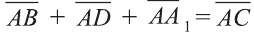
Вектор ​​​​​​= (a1; a₂; a₃) — называют умножением вектора

(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

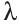
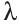
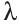
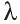
Для любых векторов и и чисел и

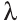
а);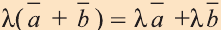

b);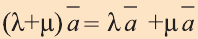

c) 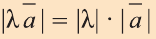и направление вектора

совпадает с направлением вектора , если ,

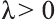
противоположно направлению вектора , если .

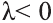
Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и . Если векторы

и сонаправлены или противоположно направлены,

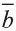
то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство , то они коллинеарны и наоборот.

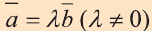
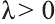
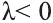
Если , то векторы и сонаправлены , если, то

противоположно направлены .

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

и наоборот.

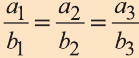
Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда (х — 1 ;у — 1; — 1).

По условию задачи векторы (х — 1 ;у — 1; — 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .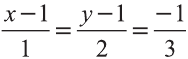

Откуда находим , .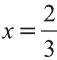

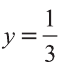
Итак,

Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).

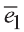
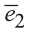
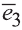
Векторы (1; 0; 0), (0; 1; 0) и (0; 0; 1) называют ортами (рис. 28).

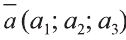
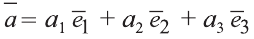
Любой вектор можно единственным образом разложить по ортам, то есть представить в виде (рис. 29).

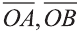
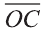
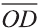
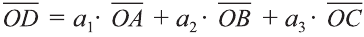
Точно также, если заданы три нeкомпланарных вектора и , то любой вектор можно единственным образом представить в виде:

.

Здесь 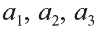некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и =, исходящих из точки О (рис. 30).

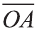
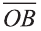
Угол между векторами и обозначают так .

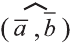
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

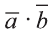
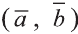
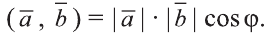
Скалярное произведение обозначают или . По определению (1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

В физике работа A, выполненная при движении тела на расстоянии , под воздействием силы (рис. 31), равна скалярному произведению силы на расстояние:

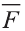
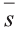
Свойство. Если 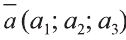и (b₁; b₂; b₃), то () =

Доказательство. Приложим векторы 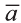и к началу

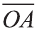
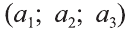
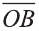
координат О (рис.32). Тогда = и = (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

Тогда .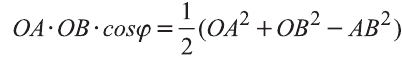

Однако, ,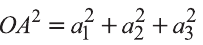

и .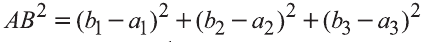

Следовательно,

.

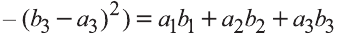
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны , также выполняется

это равенство.

Свойства скалярного произведения векторов

1. — переместительное свойство.

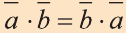
2. — распределительное свойство.

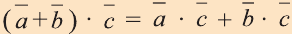
3. — сочетательное свойство.

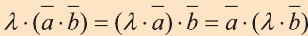
4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 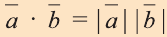, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 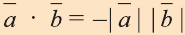, так как cos l80° = -1.

6. .

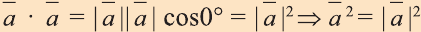
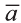
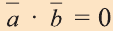
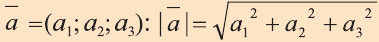
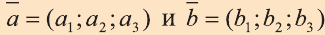
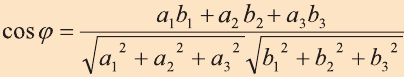
7. Если вектор перпендикулярен вектору , то . Следствия: а) Длина вектора ; (1) b) косинус угла между векторами

: ; (2)

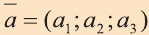
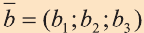
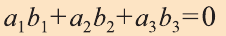
с) условие перпендикулярности векторов и

.

(3)

Пример:

— заданные точки. Найдите косинус угла между векторами .

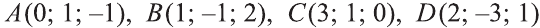
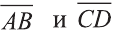
Решение:

Найдём длины векторов :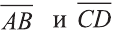

,

.

,

.

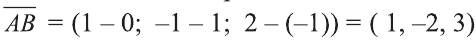
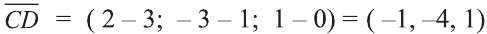
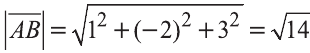
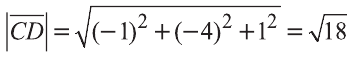
Пример:

Найдите угол между векторами .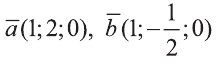

Решение:

Итак,

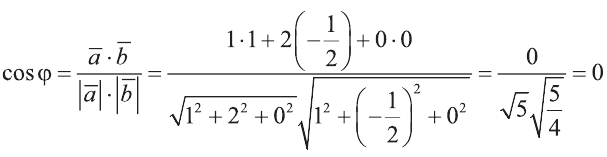
Пример:

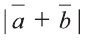
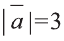
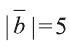
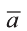
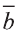
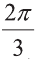
Найдите , если , и угол между векторамии равен .

Решение:

Пример:

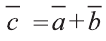
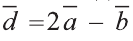
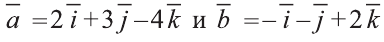
Найдите координаты и длины векторов 1); 2), если .

Решение:

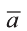
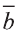
Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

. Следовательно,.

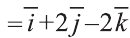
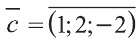
Тогда.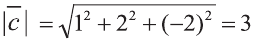

2)

.

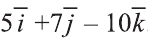
Следовательно, .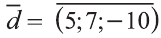

Тогда

Пример:

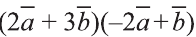
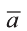
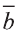
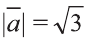
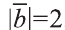
Найдите произведение, если угол между векторами и равен 30° и , .

Решение:

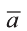
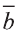
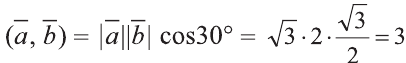
Сначала найдём поизведение векторов и :

.

Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

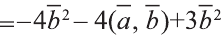
Учитывая, что ,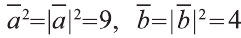

найдём искомое произведение

Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

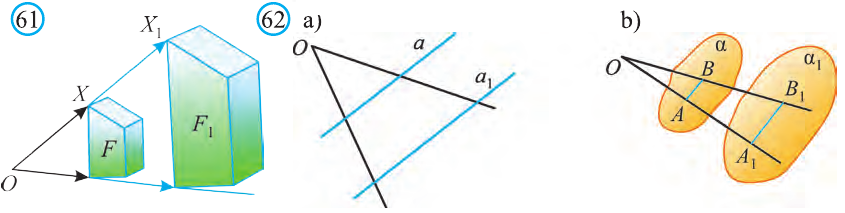
Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

Простейшим примером движения является параллельный перенос.

Пусть в пространстве даны вектор 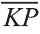и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

переносом на вектор 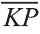, если выполняется условие . Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,

Пусть точка 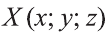фигуры F перешла в точку

фигуры F₁ при помощи параллельного переноса

на вектор .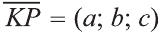

Тогда по определению получим:

или

.

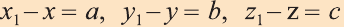
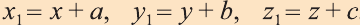
Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор 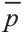= (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .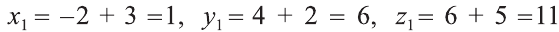

Ответ: .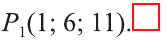

Центральная симметрия в пространстве

Если в пространстве 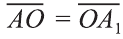, то есть точка О — середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) — искомая точка. По определению точка

О — середина отрезка АА₁. Следовательно,

Из этих уравнений получаем:

.

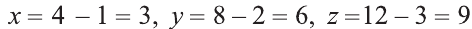
Ответ:

Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.

Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

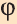
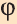
Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

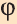
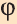
Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

Подобие пространственных фигур

Пусть 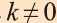и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 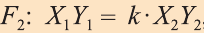, то это преобразование называют преобразованием подобия (рис. 59).

Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

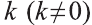
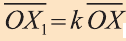
Пусть в пространстве задана фигура F, точка О и число к . Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию , называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость — в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Иррациональные числа
• Действительные числа
• Решение уравнений высших степеней
• Системы неравенств
• Уравнения и неравенства
• Уравнения и неравенства содержащие знак модуля
• Уравнение
• Метод математической индукции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Раскрывая скобки и обозначая свободный член – Ax0 – By0 – Cz0 = D, получим общее уравнение плоскости В пространстве R3:

Ax+By+Cz+D=0, A2+B2+C2>0. (4)

Итак, линейное относительно текущих координат x, y,z уравнение (4) определяет плоскость в пространстве (причем, =(A, B,C) ее нормаль). Можно показать, что верно и обратное утверждение: всякое линейное уравнение (4) в пространстве R3 определяет некоторую плоскость.

Пример. Написать уравнения координатных плоскостей.

Для того, чтобы написать уравнение любой плоскости надо знать координаты какой-нибудь точки на плоскости и какой-нибудь вектор, перпендикулярный плоскости.

В нашем примере все координатные плоскости проходят через точку M0(0,0,0) – начало координат.

А в качестве нормалей к координатным плоскостям можно взять соответственно базисные векторы .

Плоскость XOY: М0(0,0,0), (0,0,1)=(A, B,C).

0(x – 0) + 0(y – 0) + 1(z – 0)=0

Уравнение плоскости XOY: z=0.

Плоскость YOZ: M0(0,0,0), :

Уравнение плоскости YOZ: x=0.

Плоскость XOZ: M0(0,0,0), :

Уравнение плоскости XOZ: y=0.

Заметим, что в нашем примере в уравнениях координатных плоскостей отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов A, B,C равны нулю).

Уравнение плоскости (4), в котором хотя бы один из коэффициентов A, B,C или D равен нулю, называют Неполным уравнением плоскости. В этих случаях плоскость либо параллельна одной из координатных осей (один из коэффициентов A, B,C равен нулю, или, что то же, вектор нормали ортогонален одной из координатных осей); либо плоскость (4) параллельна одной из координатных плоскостей (два из коэффициентов A, B,C равны нулю, параллелен какой-нибудь координатной оси); если же коэффициент D уравнения (4) равен нулю, т. е. точка (0,0,0) удовлетворяет уравнению плоскости, плоскость проходит через начало координат.

< Предыдущая		Следующая >

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0