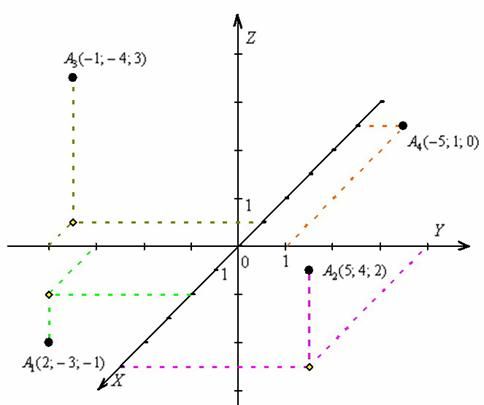
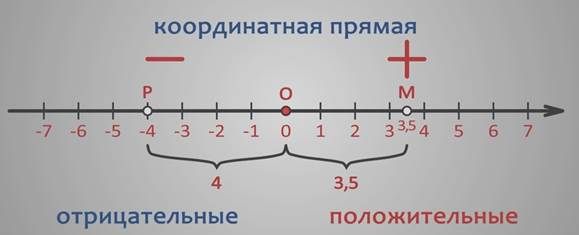
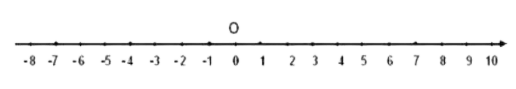Координатный луч с положительными числами дополним противоположным ему лучом и нанесём на него такие же деления. Получим координатную прямую.
Координатная прямая — это прямая с указанными на ней началом отсчёта (O )((0)), направлением и единичным отрезком.
Точка (O)( (0)) — начало отсчёта. Справа от неё отмечают положительные числа, а слева — отрицательные числа. Стрелочка указывает положительное направление отсчёта на координатной прямой.
Около стрелочки часто ставят букву (x), (y), (z) или другую букву латинского алфавита. В таких случаях говорят: ось (x), ось (y), ось (z) соответственно.
На координатной прямой важно расположение точек.
Говорят: «Точка (P) расположена слева от точки (O)». «Точка (P) расположена справа от точки (K)».
Число, показывающее положение точки на прямой, называют координатой точки.
Обрати внимание!
Единичный отрезок может быть разным на двух координатных прямых.
В данном случае единичный отрезок равен (4) клеточкам, и одной клеточке соответствует (0,25) единичного отрезка.
Запишем координаты точек (M), (K), (P), (T), (F).
M−1,5;K−1;P12;T2;F2,25.
Координатная прямая

3.9
Средняя оценка: 3.9
Всего получено оценок: 240.
3.9
Средняя оценка: 3.9
Всего получено оценок: 240.
Координаты – это основа навигации. Первоначальный простенький координатный луч дает основу для понимания морской навигации, GPS- программирования и спутникового наблюдения. А написание компьютерных игр без системы навигации главного героя в вымышленном мире вообще невозможно.
Что такое координаты?
Координаты – это числа, определяющие положение точки в пространстве. Стоит быть внимательным, при изучении этого определения.
Под пространством в геометрии понимается трехмерное пространство. Для любой точки в пространстве есть три координаты: длинны, ширины и высоты.
Но в этом определении имеется в виду не только трехмерное, но и двухмерное и одномерное пространство. В двухмерном пространстве существует всего две координаты, которые определяют положение точки в пространстве. Самые простые примеры двухмерных координатных систем это Декартова и полярная система координат.
Ярким примером декартовой системы координат является снайперский прицел. А вот полярные координаты такого применения в обыденной жизни не нашли. Эта система подразумевает использование в качестве второй координаты угла. Такой системой пользовались древние мореплаватели.
С одномерным пространством все куда проще. Точку здесь можно отметить только на координатной прямой, а для определения положения точки на этой прямой хватит и одного значения.
Использование координатной прямой
Интересен тот факт, что практически никогда координатную прямую не используют для нанесения координат. Она используется для наглядного изображения задач или сравнения чисел, упрощая решение и в том и в другом случае.
Решим небольшую задачу.
Необходимо сравнить пять чисел: $${4over6}; {8over15}; {17over4}; {26over7}$$
Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.
$${4over6}$$ обозначим отрезком ОА. Он будет меньше единичного отрезка
$${6over15}$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка
$${17over4}$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.
$${26over7}$$ обозначим отрезком ОD, который будет расположен между 3 и 4.
Значит, вместо сравнения 4 дробей, нам необходимо сравнить только две: $${5over6} и {7over15}$$.
Разложим 6 и 15 на простые числа и найдем НОК.
$$6=2*3$$
$$15=5*3$$
$$НОК=2*3*5=30$$
$${5over6}={{5*5}over{6*5}}={25over30}$$
$${7over15}={{7*2}over{15*2}}={14over30}$$
$${25over30}>{14over30}$$
Значит:
$${4over6}>{6over15}$$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.
Что мы узнали?
Мы дали понятие координатной прямой. Привели примеры и подробные объяснения. А также привели в пример задачу с координатной прямой, которую часто решают в рамках математики 6 класса.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Анастасия Займиди
5/5
-
Ольга Гнатюк
5/5
-
Артём Вековцов
5/5
-
Максим Чепурко
5/5
-
Гриша Клопов
5/5
Оценка статьи
3.9
Средняя оценка: 3.9
Всего получено оценок: 240.
А какая ваша оценка?
Введение
Вот такие отметки на дороге (рис. 1) выполняют сразу три функции.
Рис. 1. Отметки на дороге
- Измерение расстояний. Мы знаем, на сколько мы удалились от города. Или от другой подобной отметки.
- Адрес, имя. Мы знаем, где находимся. По телефону легко передать числовой адрес нашего места.
- Направление. Глядя на эти отметки, легко понять, в какой стороне находится город – начало отсчета.
Где ещё числа помогают нам ориентироваться? В кинотеатре. В зрительном зале все ряды и все кресла пронумерованы. И на нашем билете написаны номер ряда и номер места. С помощью двух этих чисел мы легко находим свое место (рис. 2).
Рис. 2. Место в кинотеатре
Раньше дома не имели номеров. Вы приезжаете в город и ищете дом купца Елисеева. Когда людей и домов не очень много, то это не очень трудно. Особенно, если вы ищете дом известного человека (рис. 3).
Рис. 3. Дом без номера
Но в современном городе с сотнями тысяч и миллионами жителей ориентироваться нам помогает нумерация домов (рис. 4).
Рис. 4. Нумерация домов
Но вернемся к дороге. Представьте, что вы вдруг оказались на дороге перед отметкой (рис. 5).
Рис. 5. Отметка
Понятно ли, где вы находитесь? Пока нет. Нужно знать еще вот что:
- В каких единицах это измерено: может, это километры, может, версты, а может, мы в Англии и это мили.
- Точка отсчета. А в какой стороне начало, город от которого отсчитывается? В какую сторону увеличиваются эти отметки?
Когда нам будут известны эти две вещи, то мы точно будем знать, где находимся.
Координатная (числовая) прямая
Моделью дороги в математике является прямая.
Две идеи (присвоить точкам имена и измерять расстояния) объединяются в одну – координатная (или числовая) прямая. Можно имена присваивать буквенные. Там даже функцию порядка можно сохранить – за идет
, за
идет
и т.д. Но с измерением расстояний тут не понятно, как поступить. Поэтому удобнее присвоить точкам на прямой числовые имена.
Для этого требуется три действия.
- Отмечаем точку, относительно которой все будет считаться, начало отсчета. Самое разумное – поставить там отметку ноль, ведь если мы находимся в этой точке, то расстояние до начала отсчета равно нулю (рис. 6).
Рис. 6. Начало отсчета
- Выбираем единицы, в которых будем измерять. Для этого нужно указать длину отрезка, которую мы будем считать единичной (рис. 7).
Рис. 7. Единичный отрезок
- Выбираем направления, куда будут увеличиваться отметки. Отметим его стрелкой. Координатная прямая готова (рис. 8).
Рис. 8. Координатная прямая
Теперь каждой точке соответствует число, адрес этой точки. Это число называют координатой.
Модель дороги
Когда мы говорим «модель дороги в математике – прямая», может возникнуть резонный вопрос: но дорога далеко не всегда бывает прямой, она может быть какой угодно формы (рис. 9).
Рис. 9. Извилистая дорога
Уточним: мы говорим о модели дороги в том случае, если речь идёт не об удобстве, а только о расстоянии и порядке.
Если мы можем двигаться исключительно по дороге (не можем срезать и т.п.), то нам неважно, какой формы дорога: за столбом с номером будет идти столб с номером
и т.д. Таким образом, для описания движения автомобиля, например, дорогу можно «выпрямить» и рассматривать модель – прямую
Координатная плоскость
В жизни мы часто сталкиваемся с ситуациями, когда упорядочивания по одному параметру недостаточно.
Например, в кинотеатре места занумерованы не от до нескольких тысяч (что значительно усложнило бы поиск места зрителем), а обозначены номером ряда и номером места в этом ряду. Таким образом, каждому месту мы ставим в соответствие две координаты (а не одну) – ряд и место (рис. 10).
Рис. 10. Ряд и место
В этом случае нам уже не будет хватать координатной прямой, понадобится координатная плоскость.
Посмотреть урок про координатную плоскость можно по ссылке: Координатная плоскость.
Определение координат точки
Давайте потренируемся определять эти координаты для разных точек.
Определим координату точки (рис. 11).
Рис. 11. Точка
Для этого измерим, сколько раз единичный отрезок уложится от начала отсчета до точки
.
раза. Точке
соответствует число
. Или точка
имеет координату
(рис. 12).
Рис. 12. Координата точки
Иногда координату записывают в скобках после названия точки (рис. 13).
Рис. 13. Запись координаты
Определим координату точки (рис. 14).
Рис. 14. Точка
Единичный отрезок поместился раз. Координата
(рис. 15).
Рис. 15. Координата точки
Можно поступить наоборот: найти точку по ее координате. Точка имеет координату
. Тогда от нуля нужно отложить
целых единичных отрезков и
(рис. 16).
Рис. 16. Расположение точки
Пусть теперь точка левее начала отсчета. Точка . Отрезок укладывается
раза. Но координата
уже занята для точки
справа (рис. 17).
Рис. 17. Расположение точки
Да и все остальные положительные числа уже использованы для координат тех точек, что находятся справа от нуля.
Но у нас остались еще отрицательные числа. Их и будем использовать для таких точек. То есть точка имеет координату
.
Две координаты, отличающиеся только знаками (то есть противоположные числа), соответствуют точкам, симметричным относительно начала координат. Например, и
соответствуют двум симметричным точкам
и
(рис. 18).
Рис. 18. Симметричные точки
Названия числовых прямых
Если числовых прямых две или больше, то, чтобы отличать одну от другой, их обозначают буквами, ,
,
и т.д. Например, в прямоугольной системе координат на плоскости две оси. Их обозначают обычно
и
. В нашем случае, хоть прямая и одна, ее все равно обычно обозначают буквой
. Кроме того, чтобы не откладывать каждый раз единичные отрезки до нужной точки, на прямой часто сразу ставят несколько отметок, соответствующих целым числам.
Определение
Итак, координатная прямая (числовая прямая) – это прямая, на которой выбраны начало отсчета, направление, масштаб (единичный отрезок).
Каждой точке соответствует число, которое называют координатой. Координата является адресом точки. По этой координате можно точно найти, где находится точка, как дом по адресу. И, наоборот, по точке можно однозначно сказать, какая у нее координата (рис. 19).
Рис. 19. Координатная прямая
Использование координатной прямой
Итак, когда же мы используем координатную прямую? Представьте, что вам по телефону нужно объяснить, где находятся эти точки на прямой (рис. 20).
Рис. 20. Точки на прямой
Мы можем взять линейку, измерить все расстояния между точками и передать по телефону.
А теперь, пусть это числовая прямая. Теперь у каждой точки есть координата, ее можно продиктовать по телефону, а на том конце ваш собеседник по этим координатам может точно так же расставить точки (рис. 21).
Рис. 21. Точки на координатной прямой
Сравнение чисел и арифметические операции с помощью числовой прямой
Итак, у нас каждой точке соответствует число и наоборот. Но соответствие распространяется и дальше – на сравнение чисел и на арифметические операции.
То, что , означает, что точка с большой координатой находится правее (рис. 22).
Рис. 22. Сравнение координат
Прибавить к числу положительное число
на прямой будет означать, что от исходной точки с координатой
отступить вправо на
единичных отрезка. Придем в точку
(рис. 23).
Рис. 23. Сложение положительных чисел
Прибавить отрицательное число (вычесть положительное) означает сдвиг влево (рис. 24).
Рис. 24. Вычитание
Свойство противоположных чисел: их сумма равна нулю. Двум противоположным числам соответствуют симметричные относительно нуля точки. Например, и
. Можно к
прибавить
, то есть сдвинуться на
единиц вправо, придем в точку ноль. Или, наоборот, от точки
можно сдвинуться на
единиц влево (прибавить отрицательное число
или вычесть
) (рис. 25).
Рис. 25. Свойство противоположных чисел
Задача
Замена в задаче чисел точками, а сложения – сдвигом может облегчить решение. Чему равна сумма бесконечного числа слагаемых: ?
Решение
Изобразим точку на прямой. Она находится посредине между
и
(рис. 26).
Рис. 26. Расположение точки
Добавить одну четвертую – значит найти точку, сдвинутую на единичного отрезка вправо, то есть на половину оставшегося до единицы (рис. 27).
Рис. 27. Добавили
Добавим к нему , то есть еще движемся вправо на
, половину оставшегося отрезка (рис. 28).
Рис. 28. Добавили
Этот процесс будет продолжаться до бесконечности, но новая точка всегда будет левее единицы, но все ближе и ближе к ней.
То есть сумма становится всё ближе к единице, но не превосходит ее. Поэтому такую бесконечную сумму считают равной единице: .
Заключение
Мы выяснили, что числовая прямая устанавливает соответствие между точками и числами. Такое взаимно-однозначное соответствие позволяет заменить работу с точками на работу с числами или наоборот. Переход от одних объектов к другим часто позволяет упростить задачу, облегчить понимание.
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. Ч. 2. М. «Просвещение», 2010.
- Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Yaklass.ru (Источник).
- Math-prosto.ru (Источник).
- School-assistant.ru (Источник).
Домашнее задание
- Укажите координату точки
(рис. 1).
Рис. 1. Иллюстрация к заданию
Введение в координатную геометрию
Система геометрии, в которой положение точек на плоскости описывается упорядоченной парой чисел.
Определение 1
Плоскость — это поверхность, бесконечно простирающаяся в обоих направлениях. Если бы мы поместили точку на плоскости, координатная геометрия дала бы нам способ точно описать, где она находится, с помощью двух чисел.

Что такое координаты?
Чтобы показать концепцию, изучим сетку выше. Столбцы помечены A, B, C и т. д. Строки сгруппированы 1, 2, 3 и т.д. сверху. Мы видим, что X располагается в ячейке D3; то есть столбик D, строчка 3.
D и 3 именуются координатами. Она состоит из двух частей: строчки и столбика. В каждой строке много полей, и в каждом столбце много полей. Номы можем найти одно безальтернативное поле, где пересекаются столбец и строка.
Координатная плоскость
В координатной геометрии точки располагаются на «координатной плоскости», как продемонстрировано ниже. Он имеет две шкалы, одна проходит вдоль плоскости, именуемой «осью x», а другая перпендикулярна ей, называемой «осью y». (Их можно изучать как подобные столбцу и строке в абзаце выше.) Точка, в которой оси пересекаются, зовётся началом координат, где x и y равны нулю.
Определение прямой в координатной геометрии
Определение 2
Прямая — геометрический объект, который является прямым, бесконечно длинным и бесконечно тонким. Его местоположение определяется двумя или более точками на прямой, координаты которых известны.
Прямая проходит через обе и бесконечно продолжается в обоих направлениях.
Это то же самое, что и определение прямой в обычной планиметрии, с той лишь разницей, что мы знаем координаты задействованных точек.
Определение луча в координатной геометрии
Определение 3
Луч — это прямая,начинающаяся в точке с заданными координатами и бесконечно уходящая в каком-то направлении. При этом он может проходить через другую точку. Это то же самое, что и определение луча в обычной плоской геометрии, с той лишь разницей, что мы знаем координаты.
Координаты
Каждой точке пространства можно присвоить три числа относительно начальной точки. Эти три числа позволяют нам отличить любую точку от любой другой в пространстве. К счастью для вас, мы имеем дело не с тремя измерениями, а только с двумя.
Определения 4 — 6
Упорядоченные пары: каждая точка на координатной плоскости называется парой чисел, порядок которых важен; эти числа записываются в круглых скобках и разделяются запятой.
Координата x: число слева от запятой в упорядоченной паре является координатой x и указывает величину перемещения по оси x от начала координат. Движение происходит вправо, если число положительное, и влево, если число отрицательное.
y- координата: число справа от запятой в упорядоченной паре является y — координатой и указывает количество движения перпендикулярно оси x. Движение выше оси x, если число положительное, и ниже оси x, если число отрицательное.
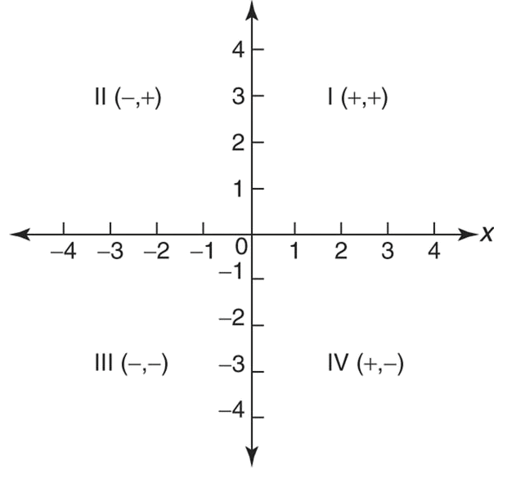
- В квадранте I x всегда положителен, а y всегда положителен.
- В квадранте II x всегда отрицателен, а y всегда положителен.
- В квадранте III x всегда отрицателен, а y всегда отрицателен.
- В квадранте IV x всегда положителен, а y всегда отрицателен.
Точка, связанная с упорядоченной парой действительных чисел, называется графом упорядоченной пары.
Пример 1
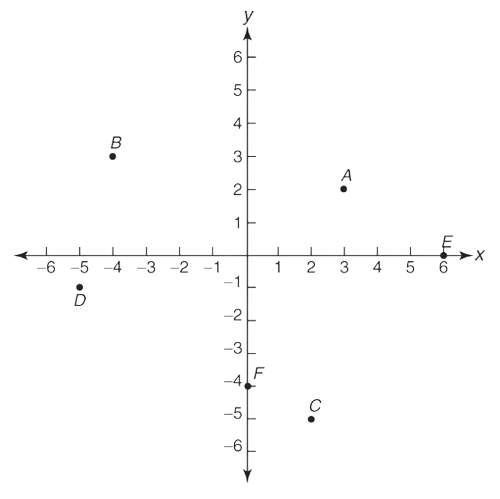
Определите A, B, C, D, E и F на графике координат на рисунке.
Нахождение координат конкретных точек на плоскости.
A (3;2), В (-4;3), C (2; -5), D (-1; -5), Е (6,0) и F (-4;0)
Нет времени решать самому?
Наши эксперты помогут!
Расстояние между двумя точками
Формула
Учитывая координаты двух точек, расстояние D определяется как:
[D=sqrt{d x^{2}+d y^{2}}]
Где:
dx — разница между x-координатами точек
dy — разница между y-координатами точек
Соответствие между точками и действительными числами
Прямая может содержать много точек. Они непосредственно связаны с действительными числами. Это можно обозначить как взаимно очевидное соответствие.
Правило
Любая точка на прямой координат соответствует одному действительному числу, а каждое любое число соответствует одной точке на прямой.
Чтобы лучше уяснить это правило, нужно обозначить точку на прямой координат и посмотреть, какому числу соответствует знак. Если эта точка соотносится с началом координат, она будет помечена нулем. Если не совпадает с началом, откладываем нужное число единичных отрезков до достижения заданного знака. Этой точке будет соответствовать число. В изложенном ниже примере воочию продемонстрируем этот постулат.
Если мы не можем отыскать точку, откладывая единичные отрезки, нам также нужно обозначить точки, составляющие десятую, сотую или тысячную часть его. Подробно это правило можно увидеть на образце.
Отложив несколько таких промежутков, мы можем получить не только целое число, но и дробное — как отрицательное, так и положительное. Помеченные промежутки помогут нам найти необходимую точку на прямой координат. Это могут быть как целые числа, так и дробные. Впрочем, на прямой есть точки, которые чрезвычайно сложно найти с помощью отдельных отрезков. Они соответствуют десятичным дробям. Чтобы найти аналогичную точку, нужно отложить один отрезок, десятую, сотую, тысячную, десятитысячную и другие части.
Множество действительных чисел включает в себя все, которые возможно записать в виде дроби.
Каждой точке на прямой координат соответствует конкретное действительное число.
Различные точки обозначают разные числа.
Если число не является целым, мы должны обозначить несколько отрезков (единичных), а также десятые, сотые доли в заданном направлении. К примеру, 400350 соответствует точке на прямой координат, в которую возможно попасть из начала координат, отложив в положительном направлении 400 единичных отрезков, 3 десятичных, и 5 тысячных.
Каждая точка на прямой соответствует действительному числу, которое помечается на координатной прямой. Из-за данного суждения прямая иногда определяется как числовая прямая.
Эта информация доступна зарегистрированным пользователям
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Начнем с сухих, но емких определений.
Определение: положительное число — это число со знаком «+» перед ним.
Обычно + не пишется, а просто подразумевается.
Числа 2, (mathbf{frac{1}{2}}), (mathbf{123frac{456}{789}}), 9871254 — перед ними не стоит никакой знак, соответственно, эти числа положительные.
Мы могли бы их записать и со знаком «+»:
+2, (mathbf{+frac{1}{2}}), (mathbf{+123frac{456}{789}}), +9871254
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Определение: отрицательное число — это число со знаком «-» перед ним.
Приведем примеры отрицательных чисел:
-3, (mathbf{-frac{1}{6}}), (mathbf{-32frac{4}{5}}), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
- Все положительные числа строго больше нуля
- Все отрицательные число строго меньше нуля
- 0 не относится ни к положительным, ни к отрицательным числам
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Эта информация доступна зарегистрированным пользователям
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Определение: Неотрицательные числа — это все положительные числа и 0.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, (mathbf{frac{4}{9}}), (mathbf{342frac{1}{9}}).
Определение: Неположительные числа — это все отрицательные числа и 0.
В данном случае примерами будут соответственно отрицательные числа или 0.
Примеры: 0, (mathbf{-1}), (mathbf{-922}), (mathbf{-frac{7}{8}}), (mathbf{-4frac{1}{4}}).
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
- Отрицательное число является неположительным
- Положительные число является неотрицательным
- 0 является одновременно и неположительным, и неотрицательным числом
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
- Неположительные числа меньше или равны нулю.
- Если а — неположительное, то (mathbf{aleq0})
- Аналогично, неотрицательные числа больше или равны нулю.
- Если a — неотрицательное, то (mathbf{ageq0})
Эта информация доступна зарегистрированным пользователям
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Определение: координатная прямая — это прямая с указанной на ней точкой начала отсчета, направлением и единичным отрезком.
Эта информация доступна зарегистрированным пользователям
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Эта информация доступна зарегистрированным пользователям
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Эта информация доступна зарегистрированным пользователям
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Эта информация доступна зарегистрированным пользователям
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
- Точка начала отсчета
- Направление
- Единичный отрезок
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Эта информация доступна зарегистрированным пользователям
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
Введем еще одно определение: координата точки — это число, показывающее положение точки на координатной прямой.
Эта информация доступна зарегистрированным пользователям
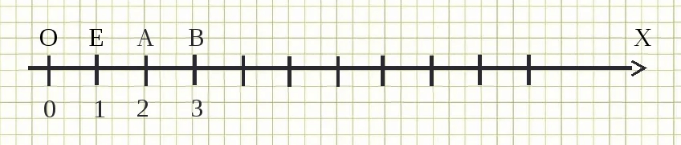
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет (mathbf{-3}).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Этот случай иллюстрирует точка D — она находится на расстоянии полутора единичных отрезков от точки начала отсчета.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна (mathbf{-1.5}).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Эта информация доступна зарегистрированным пользователям
В таком случае точки справа от точки начала отсчета будут иметь отрицательные координаты, а точки слева точки начал отсчета — положительные.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Эта информация доступна зарегистрированным пользователям
Сегодня Вы узнали про отрицательные числа. Интересно, а когда про отрицательные числа узнали впервые в истории?
Изначально люди оперировали в основном натуральными числами. Они удобны, когда надо посчитать количество голов скота, количество дней в каком- то процессе и так далее.
Мы уже обсуждали, что в какой- то момент пришлось работать с дробями, так как и они появляются в реальной жизни, когда мы говорим про половину килограмма крупы, треть часа на выполнение задания и так далее.
А отрицательных чисел в каком-то естественном эквиваленте не встретить, это все равно будет некоторая абстракция, поэтому древние люди относились к ним с недоверием.
Несмотря на это, китайские математики II века до нашей эры уже знали про них и умели применять к ним сложение и вычитание, но еще не научились их делить и умножать.
Различали же древние китайцы положительные и отрицательные числа не как мы, с помощью знаков, а с помощью цвета — положительным числам соответствовал красный цвет, а отрицательным- черный.
Так продолжалась до XII века, пока отрицательные числа не начали просто перечеркивать чертой слева направо.
Уже с VII века зафиксировано понимание того, что отрицательные числа нужны для оперирования долгами.
Условно, если у меня есть (mathbf{-5}) тысяч рублей, то это значит, что я кому- то 5 тысяч рублей должен.
Координатную прямую впервые ввел французский ученый Рене Декарт в 1637 году, что сильно поспособствовало популяризации отрицательных чисел.
Окончательно отрицательные числа закрепились только к началу XIX века.