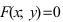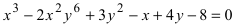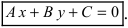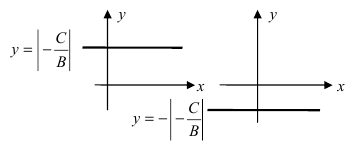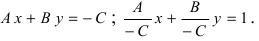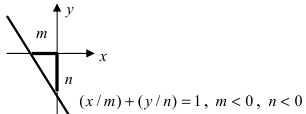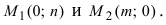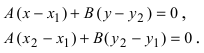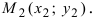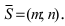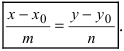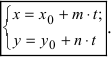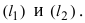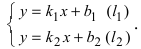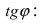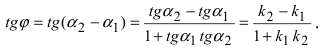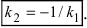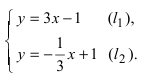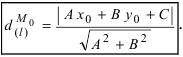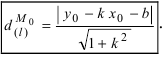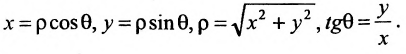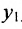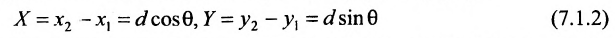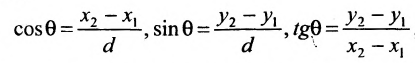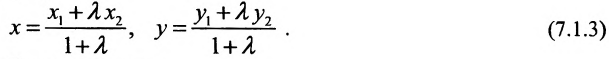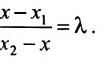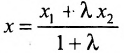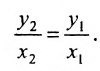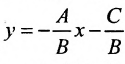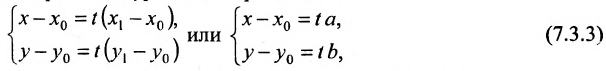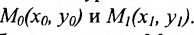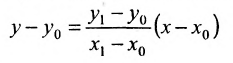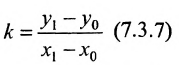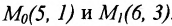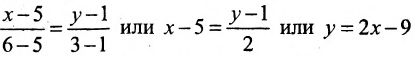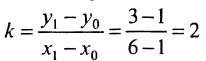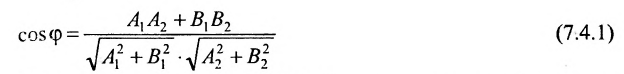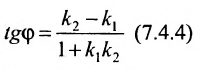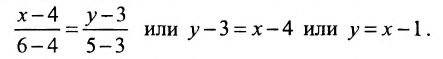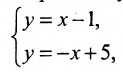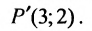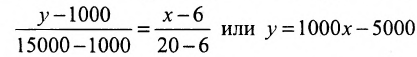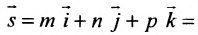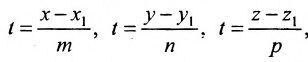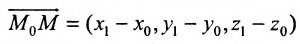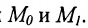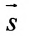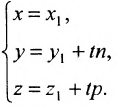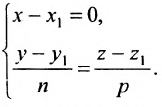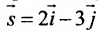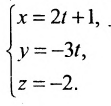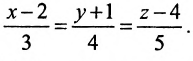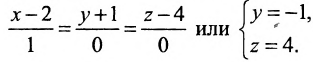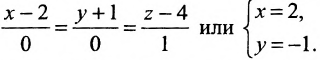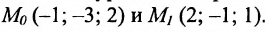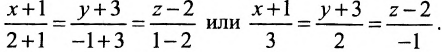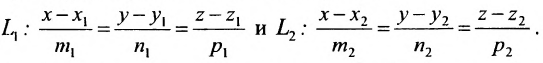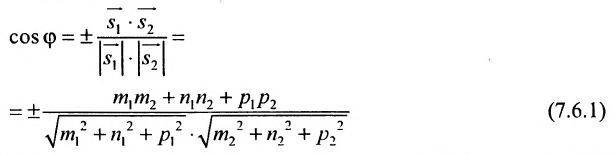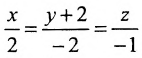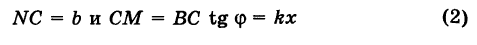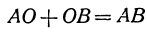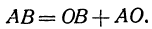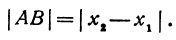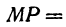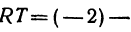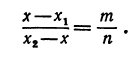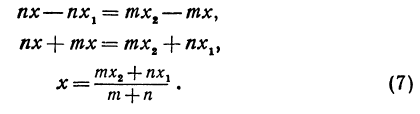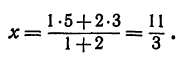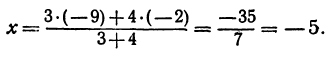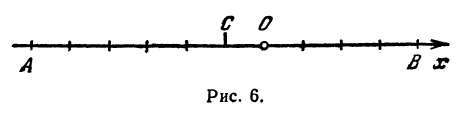Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Эта информация доступна зарегистрированным пользователям
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Начнем с сухих, но емких определений.
Определение: положительное число — это число со знаком «+» перед ним.
Обычно + не пишется, а просто подразумевается.
Числа 2, (mathbf{frac{1}{2}}), (mathbf{123frac{456}{789}}), 9871254 — перед ними не стоит никакой знак, соответственно, эти числа положительные.
Мы могли бы их записать и со знаком «+»:
+2, (mathbf{+frac{1}{2}}), (mathbf{+123frac{456}{789}}), +9871254
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Определение: отрицательное число — это число со знаком «-» перед ним.
Приведем примеры отрицательных чисел:
-3, (mathbf{-frac{1}{6}}), (mathbf{-32frac{4}{5}}), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
- Все положительные числа строго больше нуля
- Все отрицательные число строго меньше нуля
- 0 не относится ни к положительным, ни к отрицательным числам
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Эта информация доступна зарегистрированным пользователям
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Определение: Неотрицательные числа — это все положительные числа и 0.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, (mathbf{frac{4}{9}}), (mathbf{342frac{1}{9}}).
Определение: Неположительные числа — это все отрицательные числа и 0.
В данном случае примерами будут соответственно отрицательные числа или 0.
Примеры: 0, (mathbf{-1}), (mathbf{-922}), (mathbf{-frac{7}{8}}), (mathbf{-4frac{1}{4}}).
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
- Отрицательное число является неположительным
- Положительные число является неотрицательным
- 0 является одновременно и неположительным, и неотрицательным числом
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
- Неположительные числа меньше или равны нулю.
- Если а — неположительное, то (mathbf{aleq0})
- Аналогично, неотрицательные числа больше или равны нулю.
- Если a — неотрицательное, то (mathbf{ageq0})
Эта информация доступна зарегистрированным пользователям
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Определение: координатная прямая — это прямая с указанной на ней точкой начала отсчета, направлением и единичным отрезком.
Эта информация доступна зарегистрированным пользователям
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Эта информация доступна зарегистрированным пользователям
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Эта информация доступна зарегистрированным пользователям
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Эта информация доступна зарегистрированным пользователям
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
- Точка начала отсчета
- Направление
- Единичный отрезок
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Эта информация доступна зарегистрированным пользователям
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
Введем еще одно определение: координата точки — это число, показывающее положение точки на координатной прямой.
Эта информация доступна зарегистрированным пользователям
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет (mathbf{-3}).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Этот случай иллюстрирует точка D — она находится на расстоянии полутора единичных отрезков от точки начала отсчета.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна (mathbf{-1.5}).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Эта информация доступна зарегистрированным пользователям
В таком случае точки справа от точки начала отсчета будут иметь отрицательные координаты, а точки слева точки начал отсчета — положительные.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Эта информация доступна зарегистрированным пользователям
Сегодня Вы узнали про отрицательные числа. Интересно, а когда про отрицательные числа узнали впервые в истории?
Изначально люди оперировали в основном натуральными числами. Они удобны, когда надо посчитать количество голов скота, количество дней в каком- то процессе и так далее.
Мы уже обсуждали, что в какой- то момент пришлось работать с дробями, так как и они появляются в реальной жизни, когда мы говорим про половину килограмма крупы, треть часа на выполнение задания и так далее.
А отрицательных чисел в каком-то естественном эквиваленте не встретить, это все равно будет некоторая абстракция, поэтому древние люди относились к ним с недоверием.
Несмотря на это, китайские математики II века до нашей эры уже знали про них и умели применять к ним сложение и вычитание, но еще не научились их делить и умножать.
Различали же древние китайцы положительные и отрицательные числа не как мы, с помощью знаков, а с помощью цвета — положительным числам соответствовал красный цвет, а отрицательным- черный.
Так продолжалась до XII века, пока отрицательные числа не начали просто перечеркивать чертой слева направо.
Уже с VII века зафиксировано понимание того, что отрицательные числа нужны для оперирования долгами.
Условно, если у меня есть (mathbf{-5}) тысяч рублей, то это значит, что я кому- то 5 тысяч рублей должен.
Координатную прямую впервые ввел французский ученый Рене Декарт в 1637 году, что сильно поспособствовало популяризации отрицательных чисел.
Окончательно отрицательные числа закрепились только к началу XIX века.
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
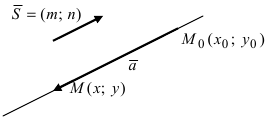
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Прямая линия на плоскости и в пространстве с примерами решения
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 — линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) — ему не удовлетворяет;
б)
в) 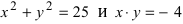
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 — уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 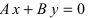
Рис. 20. Прямая, проходящая через начало координат.
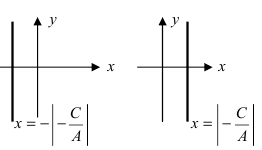
б) 5 = 0; Ах+С=0 — прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
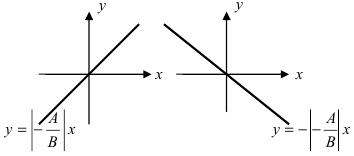
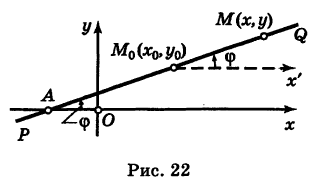
в) А = 0; Ву+С=0 — прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
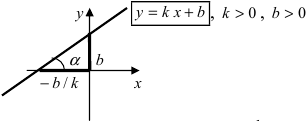
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 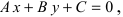
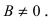
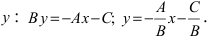
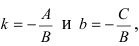
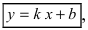
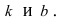
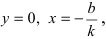
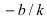
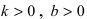
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 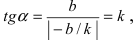
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 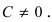
Обозначим через 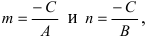
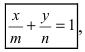
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 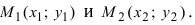
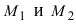
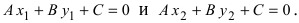
Пусть 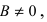
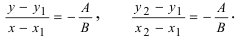
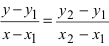
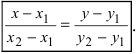
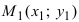
4. Уравнение прямой, проходящей через заданную точку 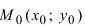
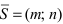
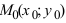
Определение: Вектор 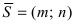
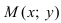
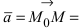
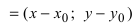
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 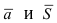
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 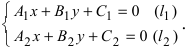
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
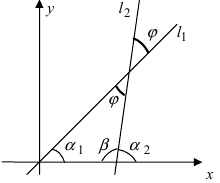
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что 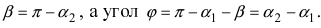
Наименьший угол между пересекающимися прямыми определим формулой 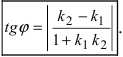
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что 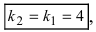
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты 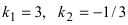
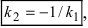
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 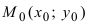
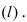
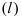
Если прямая 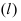
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка 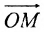
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая — второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси — координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую — осью ординат, обозначаемую Оу.
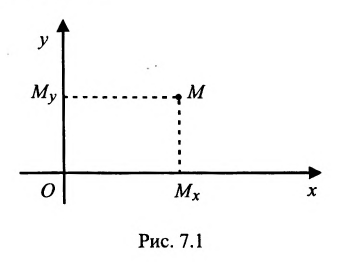
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно 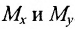
Координатами точки М в заданной системе называются числа 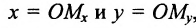
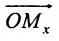
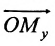
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у — М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
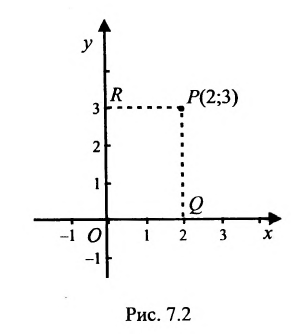
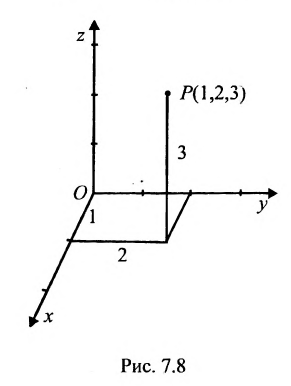
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
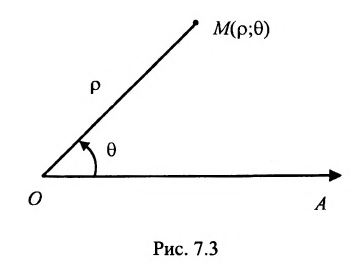
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат 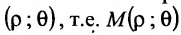
Декартова прямоугольная система координат связана с полярной системой формулами:
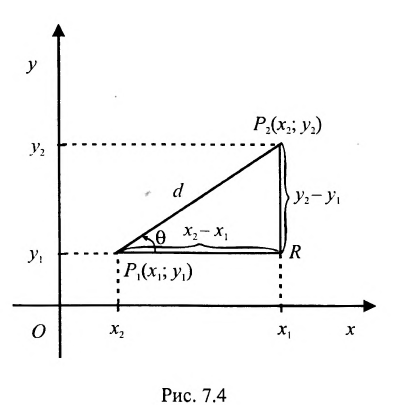
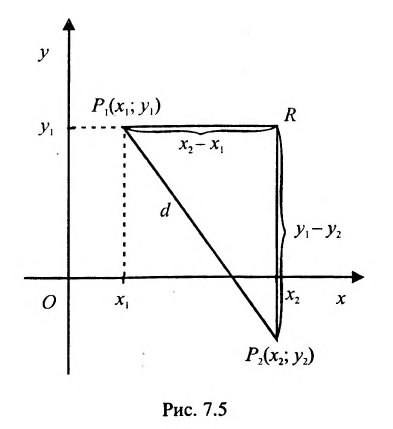
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками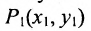
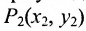
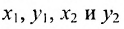
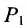
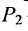
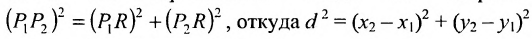
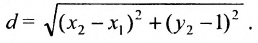
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки 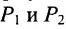
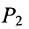
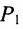
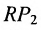
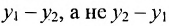
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как 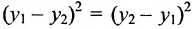
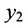
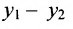
Если обозначить через 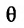
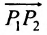
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u — произвольная ось, а 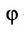
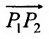
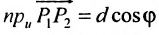
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая — второй. Обозначим их в заданном порядке через 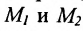
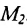
Определение 7.1.1. Число 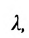
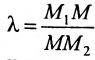
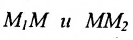
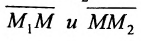
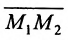
Число 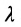
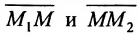
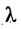
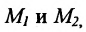
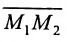
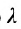
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек 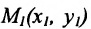
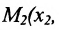
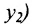
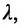
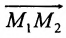
Решение задачи определяется следующей теоремой.
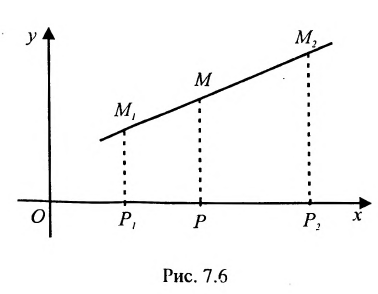
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок 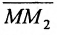
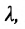
Доказательство:
Спроектируем точки 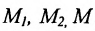
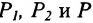
Подставив в (7.1.4) величины отрезков 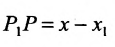
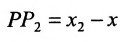
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если 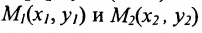
середина отрезка 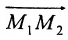
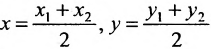
получаются из (7.1.3) при 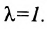
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора 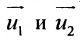
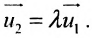
Для всех направляющих векторов 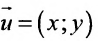
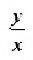
Действительно, если 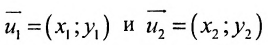
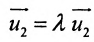
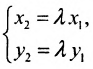
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
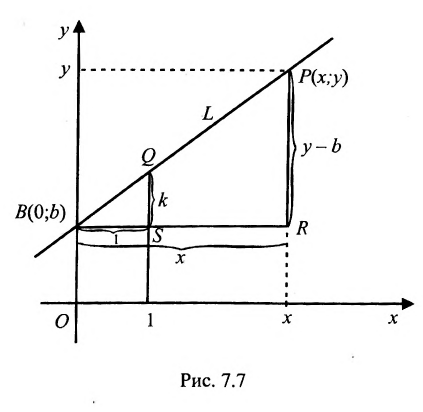
Доказательство: Пусть В = (О,b>- точка пересечения прямой L с осью у, а Р = (х,у) — любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р — прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то 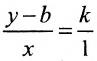
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
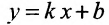
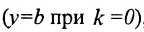
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Если 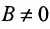
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
или 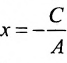
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как 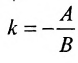
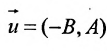
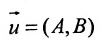
1. 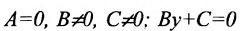
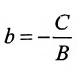
2. 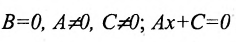
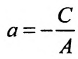
3. 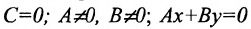
4. А=0; С=0; Ву-0 или у = 0 — это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 — это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где 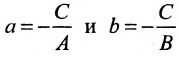
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки 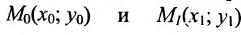
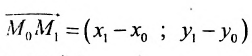
Геометрическое место концов всевозможных векторов вида 
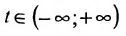
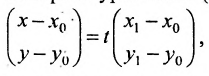
где 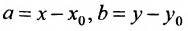
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
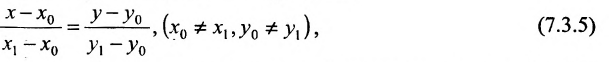
Если абсциссы точек 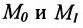

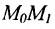
Если ординаты точек 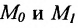
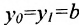
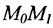
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку 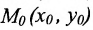
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек 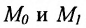
II способ. Зная координаты точек 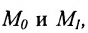
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: 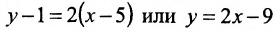
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
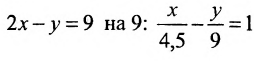
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями 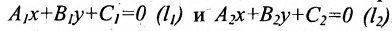
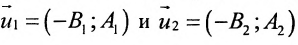
Если прямые параллельны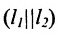
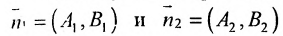
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые 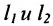
Например, прямые 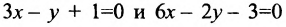
т. к.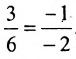
Если прямые перпендикулярны 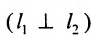
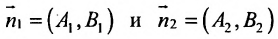
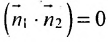
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые 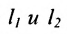
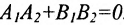
Например, прямые 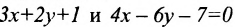
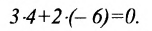
Если прямые заданы уравнениями вида 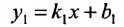
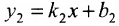
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
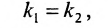
а для их перпендикулярности необходимо и достаточно, чтобы
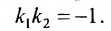
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ — это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку 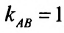
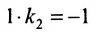
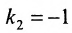
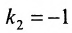
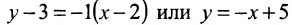
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
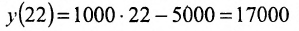
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: 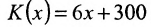
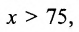
Прямая линия в пространстве
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство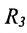
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки 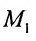
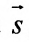
Вектор 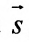
Итак, пусть прямая L проходит через точку 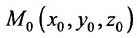
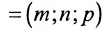
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор 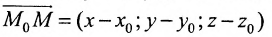
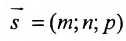
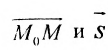
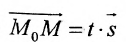
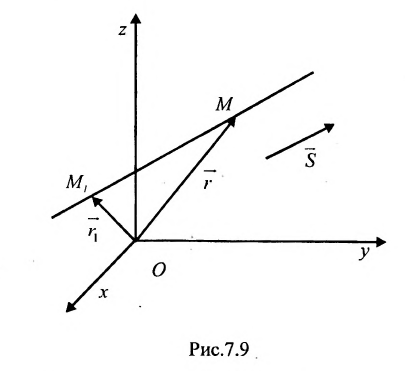
Уравнение 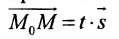
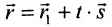
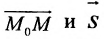
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками 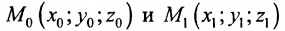
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где 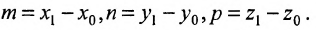
Пример:
Составить параметрические уравнения прямой, проходящей через точку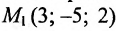
Решение:
В качестве направляющего вектора 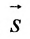
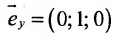
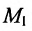
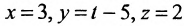
Пример:
Записать уравнения прямой 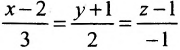
Обозначим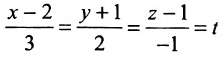
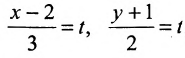
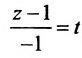
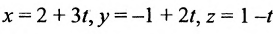
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде 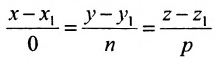
Аналогично, канонические уравнения
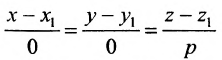
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку 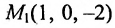
Решение:
Подставив координаты точки 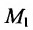
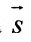
.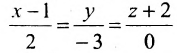
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой 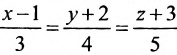
Решение:
а) Поскольку направляющий вектор заданной прямой
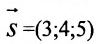
подставив координаты точки М(2; -1; 4) и вектора 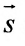
б) Поскольку единичный вектор оси О х: 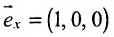
(7.5.3) координаты точки М(2; -1; 4 ) и вектора 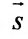
в) В качестве направляющего вектора 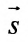
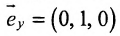
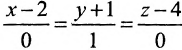
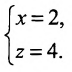
г) Единичный вектор оси Oz : 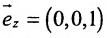
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек 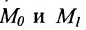
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол 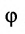
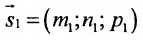
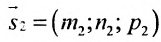
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов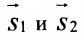
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. 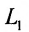
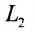
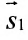
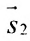
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми 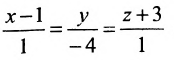
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов 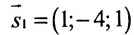
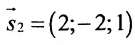
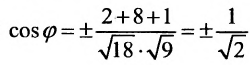
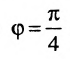
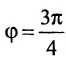
Вычисление уравнения прямой
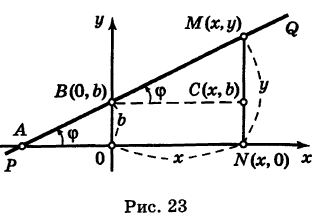
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол 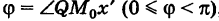
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала 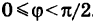
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
http://www.evkova.org/pryamaya-liniya-na-ploskosti-i-v-prostranstve
Математика
5 класс
Урок № 79
Координатный луч
Перечень рассматриваемых вопросов:
– координатный луч;
– единичный отрезок;
– соотношение единичного отрезка со знаменателем дроби;
– координата точки.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Отрезок – часть прямой, ограниченная с двух сторон точками.
Луч – это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Зададим прямую, на которой указано направление. Отметим на ней точку О. Примем её за начало отсчета.
Отложим на прямой вправо от точки О единичные отрезки.
Единичный отрезок – это расстояние от О до точки, выбранной для измерения.
Обозначим конец первого отрезка числом 1, второго – числом 2 и т. д.
Сформулируем определение.
Прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатной осью или координатным лучом.
С помощью координатной прямой натуральные числа изображаются точками.
Точке О на координатной прямой соответствует число 0. Обозначают: О (0).
Число, которое соответствует данной точке на координатной оси, называют координатой данной точки.
Например, точка А имеет координату 5.
Обозначают А (5).
Таким образом, на координатной прямой можно найти точку, соответствующую натуральному числу. Также с помощью натуральных чисел и числа ноль можно указать положение любой точки на прямой.
А теперь рассмотрим, как отметить на координатном луче дробь.
Чтобы удобно было изображать дробные числа, нужно правильно выбрать длину единичного отрезка.
Удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Например, если требуется изобразить на координатном луче дроби со знаменателем 7, единичный отрезок лучше взять длиной в 7 клеточек. В этом случае изображение дробей на координатном луче будет несложным.
можно изобразить одним единичным отрезком и ещё двумя клеточками.
Если требуется отметить на координатном луче дроби с разными знаменателями, желательно, чтобы число клеточек в единичном отрезке делилось на все знаменатели. Например, для изображения на координатном луче дробей со знаменателями 6, 4 и 12 удобно взять единичный отрезок длиной в двенадцать клеточек. Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берём таких частей столько, каков числитель.
Возьмём единичный отрезок, разделим на шесть частей и возьмём одну из них.
Тренировочные задания
№ 1. Подберите правильные названия к числам. Разместите нужные подписи под изображениями.
Варианты ответов: смешанное число; правильная дробь; неправильная дробь.
Чтобы правильно выполнить задание, необходимо вспомнить, какую дробь называют правильной, а какую неправильной. А также, что называют смешанным числом.
Правильный ответ:
Варианты ответа: 9; 6; 4; 3; 2
Мы знаем, что удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Знаменатель равен 9, значит, единичный отрезок следует выбирать в 9 клеток.
Правильный ответ: 9.
Координаты на прямой:
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:
Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число 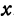
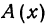
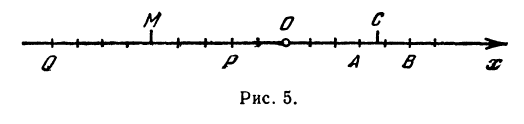
Указанные на рис. 4 точки имеют следующие координаты: 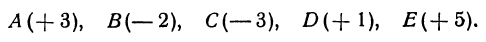
Если даны точки 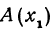
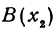
т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
- Заказать решение задач по высшей математике
Пример:
Если даны точки 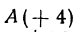
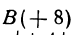
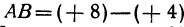
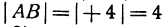
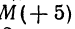
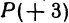
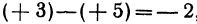
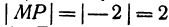
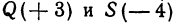
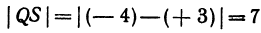
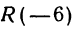
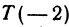
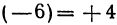
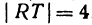
Пример:
Начало отрезка АВ находится в точке 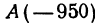
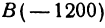
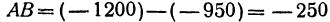
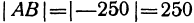
Пример:
На координатной оси даны две точки: 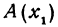
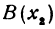
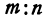
Обозначая координату искомой точки С через 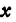
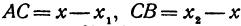
Решая последнее уравнение относительно 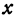
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка 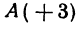
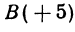
Решение:
Здесь 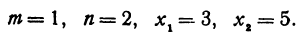
Пример:
Найти точку 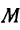
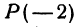
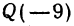
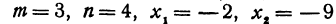
Решение:
Если 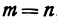
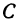
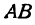
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками 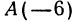
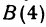
Решение:
Применяя формулу (8), получим, 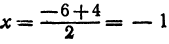
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ