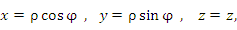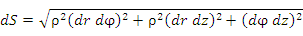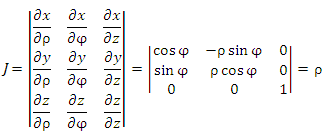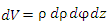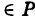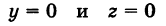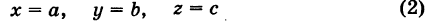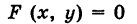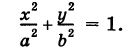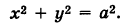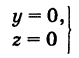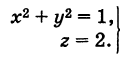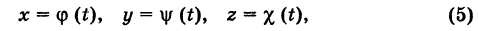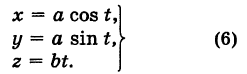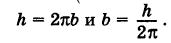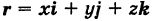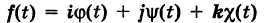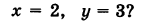Как найти координатные поверхности

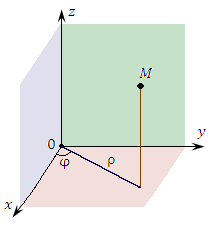
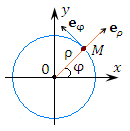
Цилиндрическая система координат

     
Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси 0z относительно координатной плоскости 0xy. Положение точки M в цилиндрической системе координат определяется тройкой чисел  ρ,  φ  и  z, где  ρ – расстояние от точки  M  до оси  0z ();  φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси  0х (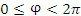);  z – проекция точки  M  на ось  0z ().

Рис. 1. Цилиндрические координаты точки M.

    
Связь между декартовыми и цилиндрическими координатами описывается формулами

     
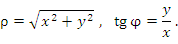
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.

      

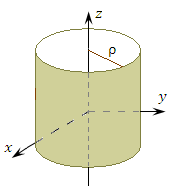
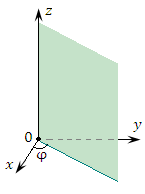
Рис. 2. Координатные поверхности цилиндрической системы координат:

круговой цилиндр (ρ = const);

полуплоскость (φ = const);

плоскость (z = const).

    
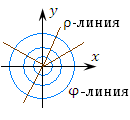
Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.

Рис. 3. Координатные ρ-линии (лучи) и φ-линии (окружности) цилиндрической системы координат.

Координатная  z-линия (прямая) направлена перпендикулярно плоскости 0xy.

    
В цилиндрической системе координатные линии, проходящие через любую точку  M  пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.

    
Единичный касательный вектор к координатной линии в точке  М, направленный в сторону возрастания координаты, называется ортом в точке  М. Поскольку цилиндрическая система координат является ортогональной, то в любой точке пространства векторы 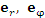и попарно ортогональны.

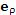
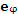
Рис. 4. Орты и цилиндрической системы координат.

Вектор 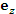направлен перпендикулярно плоскости 0xy.

    
Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.

Некоторые полезные формулы:

1. Элемент длины дуги:

   

2. Элемент площади поверхности:

   

3. Якобиан перехода от декартовой системы координат к цилиндрической:

   

4. Элемент объема:

   

---

Положение точки
в пространстве в момент времени
можно определить тройкой величин,
которые являются цилиндрическими
координатами точки (рис. 2.1). Формулы
преобразования от декартовых координат
к цилиндрическим и обратно имеют вид

, (7.1)

. (8.1)

Это так называемые
точечные преобразования; формулы этих
преобразований содержат только координаты
(«старые» и «новые»), но не содержат
явным образом временной переменной.
Последнее означает, что обе системы
координат описывают движение точки в
одной и той же (неподвижной) системе
отсчета. Области изменения цилиндрических
координат:
.

Координатные
поверхности в цилиндрической системе²:
— семейство
цилиндров кругового сечения радиуса
с осьюОz;
— семейство полуплоскостей, исходящих
из осиОz
, в которых лежат радиус-вектор точки
и осьОz;
—
семейство плоскостей, перпендикулярных
Oz. Линия
пересечения двух каких-либо координатных
поверхностей различных семейств
называется координатной линией. Так
как вдоль каждой координатной линии
меняется только одна координата, то ее
и называют соответствующей координатой.
Очевидно, координатные линии
— это концентрические окружности,
координатные линии— это полупрямые (лучи), исходящие из
начала координатО
(см. рис.
2.1), координатные линии
—
прямые, параллельные осиOz.
Так как
координатные линии
не являются прямыми, цилиндрические
координаты относятся к криволинейным.
Очевидно, что три координатные линии,
которые определяют точку пространства,
пересекают друг друга под прямыми
углами, т. е. цилиндрические координаты
являются ортогональными координатами.

Касательная,
проведенная к данной точке координатной
линии, называется координатной осью.
Все три оси цилиндрической системы
координат ортогональны друг другу.
Отложим по этим осям единичные векторы
в направлении возрастания координат и
разложим радиус-вектор точки по ортам
цилиндрических координат:

. (9.1)

Из рис. 2.1 видно,
что орты цилиндрических координат
связаны с ортами декартовых координат
соотношениями

(10.1)

Отсюда видно, что
при перемещении точки относительно S
положение ортов,
изменяется вследствие изменения угла.
Действительно, вычислим
и

(11.1)

Дифференцируя
(9.1) по t
и учитывая
(11.1), находим разложение вектора скорости
точки по ортам цилиндрической системы
координат:

. (12.1)

Аналогично,
дифференцируя
поt
и учитывая
(11.1), получим

. (13.1)

Таким образом,
проекции скорости и ускорения точки на
координатные оси
имеют вид

(14.1)

Приведем также
разложение вектора секторной скорости
точки по ортам цилиндрической системы
координат:

(15.1)

Из (14.1) и (15(1) следует,
что

. (16.1)

Рассмотрим далее
важный случай движения, при котором
секторная скорость точки остается
постоянной, т. е.
.
Введем цилиндрическую систему координат
с осью Оz,
направленной
по вектору
.
Так как,
то и радиус-вектор

и
скорость точки


в любой момент времени лежат в плоскости,
ортогональной вектору
.
В этом случае
проекции скоростейи ускоренийможно непосредственно выразить как
функциии,
а неи,
а также через производные пофункции.
Действительно, в выбранной системе
координат имеем

(17.1)

. (18.1)

Значит,

. (19.1)

Далее из (16.1) имеем
,
а

(20.1)

Так что

.
(21.1)

Формулы (19.1) и
(21.1) называют первой и второй формулами
Бине соответственно. Они оказываются
полезными при исследовании различных
случаев движения материальной точки в
центрально-симметричном силовом поле.

Пример.
Траектории точек являются плоскими и
определяются уравнениями

а)
,
б),

—
параметр,
— эксцентриситет эллипса, секторная
скорость.
Начало цилиндрических координат помещено
в фокусе эллипса. Определить ускорения
точек.

Прежде всего,
заметим, что траектории точек различны.
Так, в случае а) точка движется по эллипсу
(рис. 3.l, а), в то время как в случае б)
траектория представляет собой розетку
и не обязательно является замкнутой
кривой (рис. 3.1, б).

По второй формуле
Бине, дважды дифференцируя
по,
находим

и
в случае а),

а
ив
случае б).

Отличие в ускорениях
точек согласно уравнениям движения
означает, что действующие на точки в
случаях а) и б)
силы имеют разные законы убывания с
расстоянием от центра силы до точки. В
частности, в случае б)
сила
~
.
Если речь идет о движении планет в
гравитационном поле Солнца, то мы видим,
что в случае б)
перигелий
планеты при каждом обороте смещается
на величину
.

Пример.
Определение
радиус-вектора
точки по скорости

Определить закон
движения, траекторию и ускорение точки,
движущейся по плоской траектории с
постоянной секторной скоростью, еcли
,
где— расстояние от точки до центра,,
причем угол
между векторами
иравен.

Направим полярную
ось от центра к точке так, чтобы при
,
тогда,
а.
Отсюда,
так как если,
то.
Разделяя переменные

и интегрируя,
получим

.

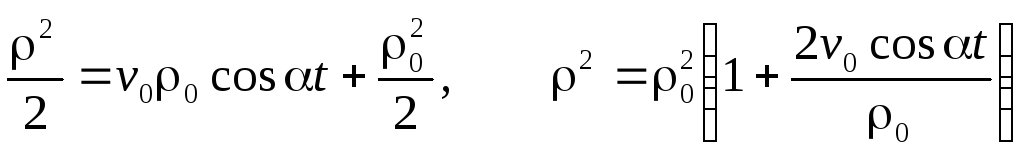
Далее найдем
:

.

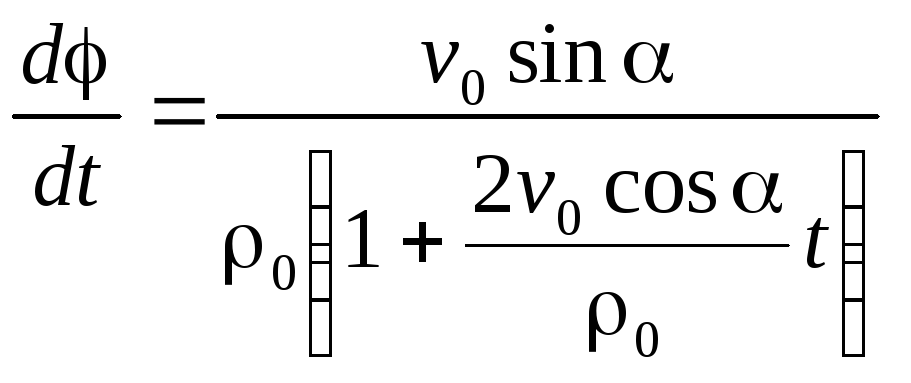
Отсюда

или

.

Ускорение точки
найдем по формуле Бине в виде:

.

Соседние файлы в папке teormeh

• #
• #
• #
• #
• #
• #

Цилиндрическая система координат (цилиндрические координаты)

Для введения цилиндрической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная система координат с полюсом и полярной осью . Через точку перпендикулярно основной плоскости проведем ось (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла, наблюдаемое со стороны положительного направления оси , происходило против часовой стрелки (рис.2.34,а).

В цилиндрической системе координат положение точки , не принадлежащей оси аппликат, характеризуется полярными координатами точки — ортогональной проекции точки на основную плоскость, и аппликатой — координатой точки — ортогональной проекции точки на ось аппликат. Таким образом, цилиндрические координаты точки — это упорядоченная тройка чисел — полярный радиус , полярный угол и аппликата . У точек, принадлежащих оси аппликат, не определен полярный угол, они задаются указанием нулевого полярного радиуса и аппликатой.

Переход от цилиндрических координат к декартовым (прямоугольным)

С цилиндрической системой координат можно связать прямоугольную систему координат (рис.2.34,б), у которой начало и базисные векторы совпадают с началом цилиндрической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим цилиндрическую систему координат (связанную с данной прямоугольной).

Поскольку аппликата точки в прямоугольной системе координат и аппликата в цилиндрической системе координат совпадают, то формулы, связывающие между собой прямоугольные координаты точки и ее цилиндрические координаты , имеют вид, следующий из

Эти формулы перехода позволяют найти прямоугольные координаты по известным цилиндрическим. Обратный переход выполняется по формулам

Главное значение полярного угла находится по формулам (см. рис.2.29).

Пример 2.12. В цилиндрической системе координат :

а) построить координатные поверхности ;

б) найти цилиндрические координаты точки , если известны ее прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны ее цилиндрические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного радиуса , является прямой круговой цилиндр, ось которого параллельна оси аппликат (рис.2.35). Этим объясняется название цилиндрической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного угла , является полуплоскость, ограниченная осью аппликат (на рис.2.35 изображены полуплоскости и ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении аппликаты , является плоскость, перпендикулярная оси аппликат (на рис.2.35 изображены плоскости и ).

б) Найдем цилиндрические координаты точки . Аппликата , полярный радиус и полярный угол находим по формулам (2.20) (см. пример 2.11):

так как и ортогональная проекция точки на координатную плоскость (основную плоскость) лежит в IV четверти.

в) Найдем прямоугольные координаты точки . По формулам (2.19) вычисляем (см. пример 2.10):

Также см. преобразования систем координат.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1. Поверхности вращения.

   Начать изучение
   

2. Эллипсоид.

   Начать изучение
   

3. Конус второго порядка.

   Начать изучение
   

4. Однополостный гиперболоид.

   Начать изучение
   

5. Двуполостный гиперболоид.

   Начать изучение
   

6. Эллиптический параболоид.

   Начать изучение
   

7. Гиперболический параболоид.

   Начать изучение
   

Поверхности вращения.

Рассмотрим линию (L), которая лежит в плоскости (P), проходящей через ось вращения (d) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.

Выберем начало декартовой прямоугольной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) на оси (d), вектор (boldsymbol{e}_{3}) направим вдоль (d), а вектор (boldsymbol{e}_{1}) поместим в плоскости (P). Таким образом, (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) — декартова система координат в плоскости (P). Пусть линия (L) имеет в этой системе координат уравнение (f(x, y)=0).

Рассмотрим точку (M(x, y, z)). Через нее проходит окружность, которая имеет центр на оси (d) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от (M) до оси, то есть (sqrt{x^{2}+y^{2}}). Точка (M) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии (L).

Точка (M_{1}(x_{1}, y_{1}, z_{1})) лежит в плоскости (P), и потому (y_{1}=0). Кроме того, (z_{1}=z) и (|x|=sqrt{x^{2}+y^{2}}), так как (M_{1}) лежит на той же окружности, что и (M). Координаты точки (M_{1}) удовлетворяют уравнению линии (L): (f(x_{1}, z_{1})=0). Подставляя в это уравнение (x_{1}) и (z_{1}), мы получаем условие на координаты точки (M), необходимое и достаточное для того, чтобы (M) лежала на поверхности вращения (S): равенство
$$
fleft(pm sqrt{x^{2}+y^{2}}, zright)=0label{ref1}
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
fleft(sqrt{x^{2}+y^{2}}, zright)fleft(-sqrt{x^{2}+y^{2}}, zright)=0,label{ref2}
$$
и является уравнением поверхности вращения линии (L) вокруг оси (d).

Эллипсоид.

Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор (boldsymbol{e}_{3}) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
frac{x^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}}{c^{2}}=1.nonumber
$$
(Здесь через (c) обозначена малая полуось эллипса.) В силу формулы eqref{ref1} уравнениями соответствующих поверхностей вращения будут
$$
frac{x^{2}+y^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}+y^{2}}{c^{2}}=1 (a > c).label{ref3}
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).

Каждую точку (M(x, y, z)) на сжатом эллипсоиде вращения сдвинем к плоскости (y=0) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении (lambda < 1). После сдвига точка попадет в положение (M'(x’, y’, z’)), где (x’=x), (y’=y), (z’=z).

Таким образом, точки эллипсоида вращения переходят в точки поверхности с уравнением
$$
frac{x’^{2}}{a^{2}}+frac{y’^{2}}{b^{2}}+frac{z’^{2}}{c^{2}}=1,label{ref4}
$$
где (b=lambda a). Поверхность, которая в некоторой декартовой системе координат имеет уравнение eqref{ref4}, называется эллипсоидом (рис. 10.3). Если случайно окажется, что (b=c), мы получим снова эллипсоид вращения, но уже вытянутый.

Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения eqref{ref4} видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.

Эллипсоид можно получить из сферы (x^{2}+y^{2}+z^{2}=a^{2}) сжатиями к плоскостям (y=0) и (z=0) в отношениях (lambda=b/a) и (mu=c/a).

В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.

Конус второго порядка.

Рассмотрим на плоскости (P) пару пересекающихся прямых, задаваемую в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) уравнением (a^{2}x^{2}-c^{2}z^{2}=0). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^{2}(x^{2}+y^{2})-c^{2}z^{2}=0label{ref5}
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости (y=0) переводит прямой круговой конус в поверхность с уравнением
$$
a^{2}x^{2}+b^{2}y^{2}-c^{2}z^{2}=0label{ref6}
$$
называемую конусом второго порядка.

Обратите внимание на то, что левая часть уравнения eqref{ref6} — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.

Однополостный гиперболоид.

Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
frac{x^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле eqref{ref1} мы получаем уравнение этой поверхности (рис. 10.5)
$$
frac{x^{2}+y^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1.label{ref7}
$$

В результате сжатия однополостного гиперболоида вращения к плоскости (y=0) мы получаем однополостный гиперболоид с уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}-frac{z^{2}}{c^{2}}=1.label{ref8}
$$

Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.

Уравнение eqref{ref8} можно переписать в виде
$$
left(frac{x}{a}+frac{z}{c}right)left(frac{x}{a}-frac{z}{c}right)=left(1+frac{y}{b}right)left(1-frac{y}{b}right).nonumber
$$

Рассмотрим прямую линию с уравнениями
$$
begin{array}{cc}
& displaystylemuleft(frac{x}{a}+frac{z}{c}right)=lambdaleft(1+frac{y}{b}right),\
& \
& displaystylelambdaleft(frac{x}{a}-frac{z}{c}right)=muleft(1-frac{y}{b}right),
end{array}label{ref9}
$$
где (lambda) и (mu) — некоторые числа ((lambda^{2}+mu^{2} neq 0)). Координаты каждой точки прямой удовлетворяют обоим уравнениям, а следовательно, и уравнению eqref{ref8}, которое получается их почленным перемножением. Поэтому каковы бы ни были (lambda) и (mu), прямая с уравнениями eqref{ref9} лежит на однополостном гиперболоиде. Таким образом, система eqref{ref9} определяет семейство прямолинейных образующих.

Второе семейство прямолинейных образующих определяется системой
$$
begin{array}{cc}
& mu’left(frac{x}{a}+frac{z}{c}right)=lambda’left(1-frac{y}{b}right),\
& \
& lambda’left(frac{x}{a}-frac{z}{c}right)=mu’left(1+frac{y}{b}right),
end{array}label{ref10}
$$

Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность (x^{2}+y^{2}-z^{2}=0) и точку (M_{0}(1, 1, 1)) на ней. Подставляя координаты (M_{0}) в уравнения eqref{ref9}, мы получаем условия на (lambda) и (mu): (2lambda=2mu) и (0 cdot lambda=0 cdot mu). Первое из них определяет (lambda) и (mu) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в eqref{ref9}, получаем уравнения прямолинейной образующей
$$
x+z=1+y, x-z=1-y.nonumber
$$

Она проходит через (M_{0}), так как (lambda) и (mu) так и выбирались, чтобы координаты (M_{0}) удовлетворяли этой системе. Аналогично, подставляя координаты (M_{0}) в (10), находим условия на (lambda’) и (mu’): (2mu’=0) и (2mu’=0). Коэффициент (lambda’) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: (x=z), (y=1).

Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.

Двуполостный гиперболоид.

Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}=1nonumber
$$
вокруг той оси, которая ее пересекает. По формуле eqref{ref1} мы получаем уравнение двуполостного гиперболоида вращения
$$
frac{z^{2}}{c^{2}}-frac{x^{2}+y^{2}}{a^{2}}=1.label{ref11}
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref12}
$$

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида eqref{ref12}, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.

Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.

Эллиптический параболоид.

Вращая параболу (x^{2}=2pz) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^{2}+y^{2}=2pz.label{ref13}
$$
Она называется параболоидом вращения. Сжатие к плоскости (y=0) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=2z.label{ref14}
$$

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).

Гиперболический параболоид.

По аналогии с уравнением eqref{ref14} мы можем написать уравнение
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=2z.label{ref15}
$$

Поверхность, которая имеет уравнение вида eqref{ref15} в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.

Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью (x=alpha) при произвольном (alpha). В этой плоскости выберем декартову прямоугольную систему координат (O’, boldsymbol{e}_{2}, boldsymbol{e}_{3}) с началом в точке (O'(alpha, 0, 0)). Относительно этой системы координат линия пересечения имеет уравнение
$$
-frac{y^{2}}{b^{2}}=2left(z-frac{alpha^{2}}{2a^{2}}right).label{ref16}
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку (O″) с координатами ((0, alpha^{2}/(2a^{2}))). (Координаты этой точки относительно исходной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) в пространстве равны ((alpha, 0, alpha^{2}/(2a^{2}))).)

Точка (O″), очевидно, является вершиной параболы, ось параболы параллельна вектору (boldsymbol{e}_{3}), а знак минус в левой части равенства eqref{ref16} означает, что ветви параболы направлены в сторону, противоположную направлению (boldsymbol{e}_{3}). Заметим, что после переноса начала координат в точку (O″) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями (x=alpha) при всех (alpha) представляют собой равные параболы.

Будем теперь менять величину (alpha) и проследим за перемещением вершины параболы (O″) в зависимости от (alpha). Из приведенных выше координат точки (O″) следует, что эта точка перемещается по линии с уравнениями
$$
z=frac{x^{2}}{2a^{2}}, y=0nonumber
$$
в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). Эта линия — парабола в плоскости (y=0). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор (boldsymbol{e}_{3}).

Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.

При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).

Сечения гиперболического параболоида плоскостями с уравнениями (z=alpha) при всевозможных (alpha) — гиперболы. Эти сечения нарисованы на рис. 10.9.

Гиперболический параболоид, как и однополостный гиперболоид, имеет два семейства прямолинейных образующих (рис. 10.10). Уравнения одного семейства —
$$
lambdaleft(frac{x}{a}-frac{y}{b}right)=mu, muleft(frac{x}{a}+frac{y}{b}right)=2lambda z,nonumber
$$
а другого —
$$
lambda’left(frac{x}{a}+frac{y}{b}right)=mu’, mu’left(frac{x}{a}-frac{y}{b}right)=2lambda’ z,nonumber
$$

Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

х = 0

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

Формула 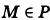обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

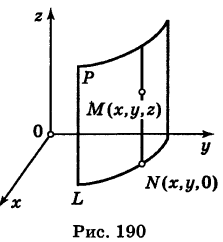
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 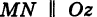(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

Пусть

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

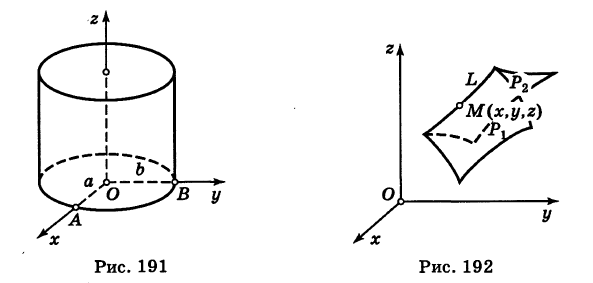
Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

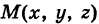
Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 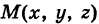, координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

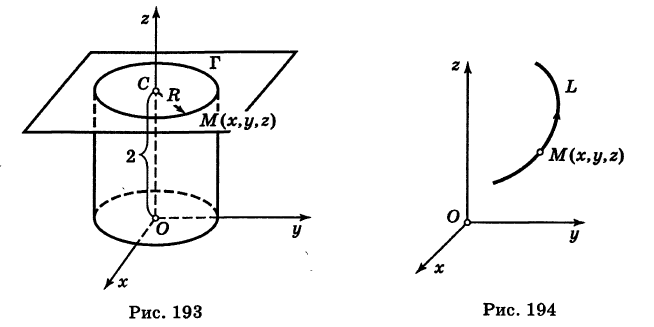
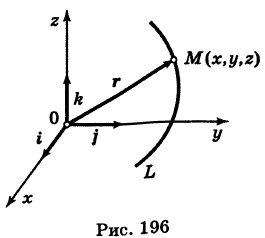
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где — некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)} не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

• Заказать решение задач по высшей математике

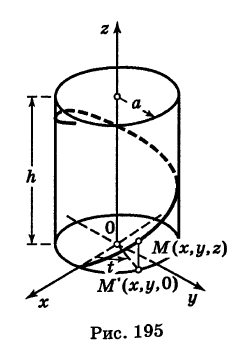
Пример:

Написать уравнения винтовой линии радиуса а и шага 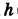(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 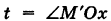и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

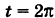
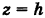
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

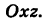
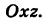
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

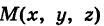
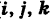
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

где

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

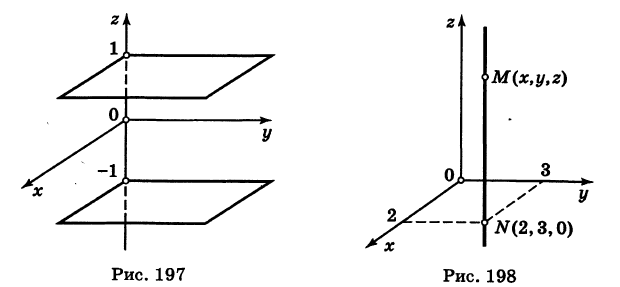
Пример:

Какой геометрический образ соответствует уравнению

Решение:

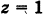
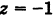
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).