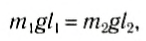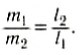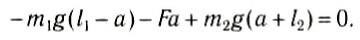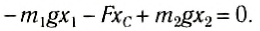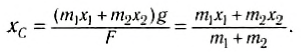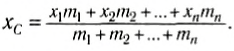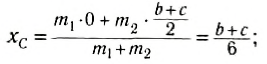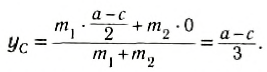Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Сущность понятия «центр масс»
Понятие «центр масс» широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.
Определение 1
Центр масс — точка, характеризующая размещение и движение исследуемой системы как единого целого.
Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке «15 см». Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.
Нахождение координат центра масс
Определение 2
Центр масс двух тел с точечными массами $m_1$ и $m_2$ и координатами на координатной прямой $x_1$ и $x_2$ находится в точке, делящей расстояние между этими телами на отрезки с длинами обратно пропорциональными массам рассматриваемых тел.
Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.
Расстояние между точечными телами равно:
$Delta x = x_2 — x_1$
Пропорция между массами и расстояниями, согласно определению:
$frac{l_1}{l_2} = frac{m_2}{m_1}$,
«Как найти координаты центра масс» 👇
где $l_1$, $l_2$ — расстояния от соответствующих тел до центра масс.
Выразив, длины через координаты
$l_1 = x_c — x_1; l_2 = x_2 — x_c$,
центр масс можно определить как
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.
где $x_c$ — координата центра тяжести.
Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):
$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$
В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.
Замечание 1
Центр тяжести системы тел представляет собой точку, подобную центру масс, но рассчитывается не для масс, а для весов (обусловленных гравитацией сил), действующих на точечные тела, входящие в систему. Центр тяжести определяется так же, как и центр масс, если размеры системы малы в сравнении с радиусом планеты Земля. Он в большинстве случаев с достаточной для практики точностью совпадает с центром масс рассматриваемой системы.
Пример 1
Найти центр масс двух линеек, изготовленных из одинакового материала, одинаковой толщины и ширины, левые концы линеек совмещены. Длины линеек — 10 и 30 см. Толщиной линеек можно пренебречь.
Поскольку толщиной можно пренебречь, найти нужно лишь координату центра масс по оси $x$.
Разобьем мысленно систему на два отрезка. Первый — где толщина линеек складывается. Его координаты — $[0, 10]$. Второй отрезок — где длинная линейка продолжается одна. Его координаты — $[10, 30]$. Примем за единицу измерения массу одного погонного сантиметра линейки. Тогда масса второго фрагмента:
$m_2 = 30 — 10 = 20$
На каждый сантиметр первого фрагмента приходится вдвое больше массы, поскольку там сложены две линейки:
$m_1 = 10 cdot 2 = 20$
Центры масс отрезков находятся на их осях симметрии, т.е. на середине длины каждого:
$x_{c1} = frac{10}{2} = 5$;
$x_{c2} = 10 + frac{20}{2} = 20$
Подставим значения в формулу:
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$
$x_c = frac{20 cdot 5 + 20 cdot 20}{20 +20} = frac{100 + 400}{40} = 12, 5$
Ответ: центр масс находится на расстоянии 12,5 см от левого конца системы линеек.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
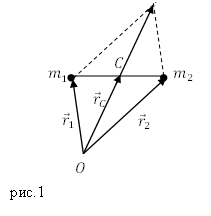
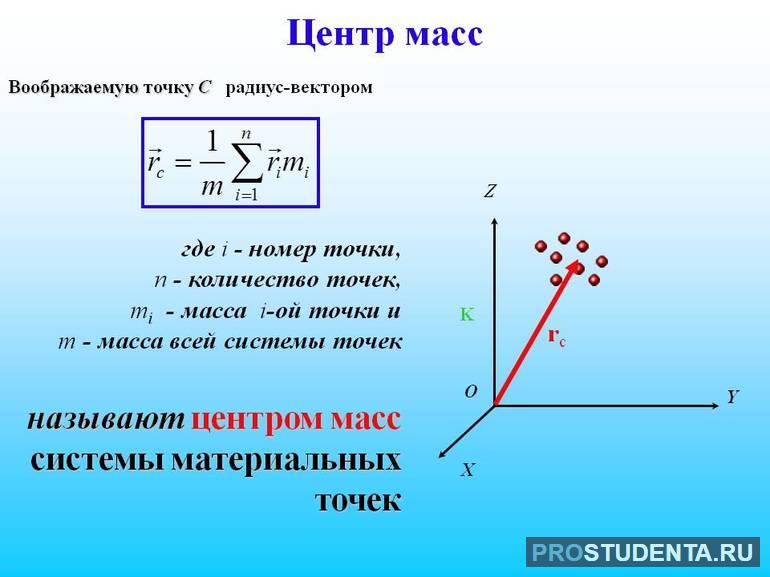
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
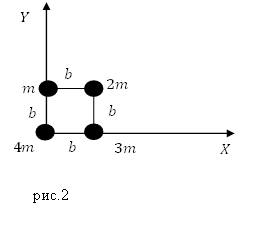
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
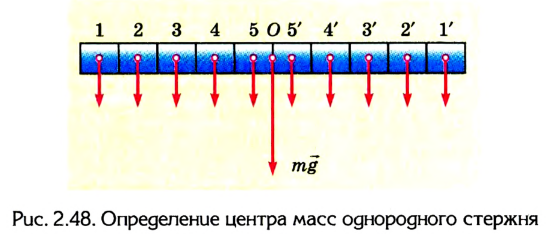
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
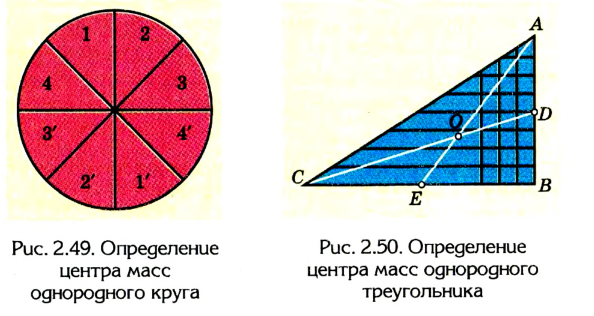
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
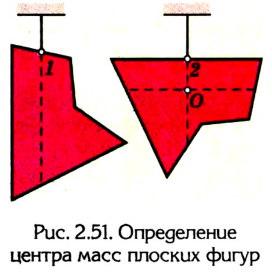
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
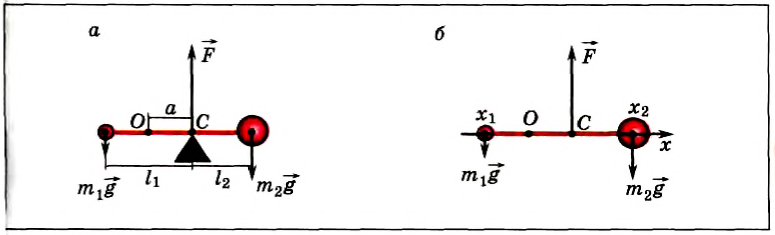
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =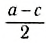
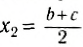
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
This toy uses the principles of center of mass to keep balance when sitting on a finger.
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton’s laws of motion.
In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe. In the case of a distribution of separate bodies, such as the planets of the Solar System, the center of mass may not correspond to the position of any individual member of the system.
The center of mass is a useful reference point for calculations in mechanics that involve masses distributed in space, such as the linear and angular momentum of planetary bodies and rigid body dynamics. In orbital mechanics, the equations of motion of planets are formulated as point masses located at the centers of mass. The center of mass frame is an inertial frame in which the center of mass of a system is at rest with respect to the origin of the coordinate system.
History[edit]
The concept of center of gravity or weight was studied extensively by the ancient Greek mathematician, physicist, and engineer Archimedes of Syracuse. He worked with simplified assumptions about gravity that amount to a uniform field, thus arriving at the mathematical properties of what we now call the center of mass. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point—their center of mass. In his work On Floating Bodies, Archimedes demonstrated that the orientation of a floating object is the one that makes its center of mass as low as possible. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes.[1]
Other ancient mathematicians who contributed to the theory of the center of mass include Hero of Alexandria and Pappus of Alexandria. In the Renaissance and Early Modern periods, work by Guido Ubaldi, Francesco Maurolico,[2] Federico Commandino,[3] Evangelista Torricelli, Simon Stevin,[4] Luca Valerio,[5] Jean-Charles de la Faille, Paul Guldin,[6] John Wallis, Christiaan Huygens,[7] Louis Carré, Pierre Varignon, and Alexis Clairaut expanded the concept further.[8]
Newton’s second law is reformulated with respect to the center of mass in Euler’s first law.[9]
Definition[edit]
The center of mass is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero. In analogy to statistics, the center of mass is the mean location of a distribution of mass in space.
A system of particles[edit]
In the case of a system of particles Pi, i = 1, …, n , each with mass mi that are located in space with coordinates ri, i = 1, …, n , the coordinates R of the center of mass satisfy the condition

Solving this equation for R yields the formula

where 
A continuous volume[edit]
If the mass distribution is continuous with the density ρ(r) within a solid Q, then the integral of the weighted position coordinates of the points in this volume relative to the center of mass R over the volume V is zero, that is
Solve this equation for the coordinates R to obtain
where M is the total mass in the volume.
If a continuous mass distribution has uniform density, which means that ρ is constant, then the center of mass is the same as the centroid of the volume.[10]
Barycentric coordinates[edit]
The coordinates R of the center of mass of a two-particle system, P1 and P2, with masses m1 and m2 is given by
Let the percentage of the total mass divided between these two particles vary from 100% P1 and 0% P2 through 50% P1 and 50% P2 to 0% P1 and 100% P2, then the center of mass R moves along the line from P1 to P2. The percentages of mass at each point can be viewed as projective coordinates of the point R on this line, and are termed barycentric coordinates. Another way of interpreting the process here is the mechanical balancing of moments about an arbitrary point. The numerator gives the total moment that is then balanced by an equivalent total force at the center of mass. This can be generalized to three points and four points to define projective coordinates in the plane, and in space, respectively.
Systems with periodic boundary conditions[edit]
For particles in a system with periodic boundary conditions two particles can be neighbours even though they are on opposite sides of the system. This occurs often in molecular dynamics simulations, for example, in which clusters form at random locations and sometimes neighbouring atoms cross the periodic boundary. When a cluster straddles the periodic boundary, a naive calculation of the center of mass will be incorrect. A generalized method for calculating the center of mass for periodic systems is to treat each coordinate, x and y and/or z, as if it were on a circle instead of a line.[11] The calculation takes every particle’s x coordinate and maps it to an angle,
where xmax is the system size in the x direction and 


In the 




where M is the sum of the masses of all of the particles.
These values are mapped back into a new angle, 
The process can be repeated for all dimensions of the system to determine the complete center of mass. The utility of the algorithm is that it allows the mathematics to determine where the «best» center of mass is, instead of guessing or using cluster analysis to «unfold» a cluster straddling the periodic boundaries. If both average values are zero, 

Center of gravity[edit]
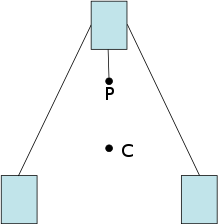
Diagram of an educational toy that balances on a point: the center of mass (C) settles below its support (P)
A body’s center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform, the mass-center and the center-of-gravity will be the same. However, for satellites in orbit around a planet, in the absence of other torques being applied to a satellite, the slight variation (gradient) in gravitational field between closer-to (stronger) and further-from (weaker) the planet can lead to a torque that will tend to align the satellite such that its long axis is vertical. In such a case, it is important to make the distinction between the center-of-gravity and the mass-center. Any horizontal offset between the two will result in an applied torque.
It is useful to note that the mass-center is a fixed property for a given rigid body (e.g. with no slosh or articulation), whereas the center-of-gravity may, in addition, depend upon its orientation in a non-uniform gravitational field. In the latter case, the center-of-gravity will always be located somewhat closer to the main attractive body as compared to the mass-center, and thus will change its position in the body of interest as its orientation is changed.
In the study of the dynamics of aircraft, vehicles and vessels, forces and moments need to be resolved relative to the mass center. That is true independent of whether gravity itself is a consideration. Referring to the mass-center as the center-of-gravity is something of a colloquialism, but it is in common usage and when gravity gradient effects are negligible, center-of-gravity and mass-center are the same and are used interchangeably.
In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body. Consider a body Q of volume V with density ρ(r) at each point r in the volume. In a parallel gravity field the force f at each point r is given by,
where dm is the mass at the point r, g is the acceleration of gravity, and 
Choose a reference point R in the volume and compute the resultant force and torque at this point,

and

If the reference point R is chosen so that it is the center of mass, then
which means the resultant torque T = 0. Because the resultant torque is zero the body will move as though it is a particle with its mass concentrated at the center of mass.
By selecting the center of gravity as the reference point for a rigid body, the gravity forces will not cause the body to rotate, which means the weight of the body can be considered to be concentrated at the center of mass.
Linear and angular momentum[edit]
The linear and angular momentum of a collection of particles can be simplified by measuring the position and velocity of the particles relative to the center of mass. Let the system of particles Pi, i = 1, …, n of masses mi be located at the coordinates ri with velocities vi. Select a reference point R and compute the relative position and velocity vectors,
The total linear momentum and angular momentum of the system are

and
![{displaystyle mathbf {L} =sum _{i=1}^{n}m_{i}(mathbf {r} _{i}-mathbf {R} )times {frac {d}{dt}}(mathbf {r} _{i}-mathbf {R} )+left(sum _{i=1}^{n}m_{i}right)left[mathbf {R} times {frac {d}{dt}}(mathbf {r} _{i}-mathbf {R} )+(mathbf {r} _{i}-mathbf {R} )times mathbf {v} right]+left(sum _{i=1}^{n}m_{i}right)mathbf {R} times mathbf {v} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d6d3b84ccbaeb3ade8c86e43b70cd5b864c6ff2)
If R is chosen as the center of mass these equations simplify to
where m is the total mass of all the particles, p is the linear momentum, and L is the angular momentum.
The law of conservation of momentum predicts that for any system not subjected to external forces the momentum of the system will remain constant, which means the center of mass will move with constant velocity. This applies for all systems with classical internal forces, including magnetic fields, electric fields, chemical reactions, and so on. More formally, this is true for any internal forces that cancel in accordance with Newton’s Third Law.[12]
Locating the center of mass[edit]
The experimental determination of a body’s centre of mass makes use of gravity forces on the body and is based on the fact that the centre of mass is the same as the centre of gravity in the parallel gravity field near the earth’s surface.
The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.[13]
In two dimensions[edit]
An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass.[14]
The shape of an object might already be mathematically determined, but it may be too complex to use a known formula. In this case, one can subdivide the complex shape into simpler, more elementary shapes, whose centers of mass are easy to find. If the total mass and center of mass can be determined for each area, then the center of mass of the whole is the weighted average of the centers.[15] This method can even work for objects with holes, which can be accounted for as negative masses.[16]
A direct development of the planimeter known as an integraph, or integerometer, can be used to establish the position of the centroid or center of mass of an irregular two-dimensional shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to compare with the required displacement and center of buoyancy of a ship, and ensure it would not capsize.[17][18]
In three dimensions[edit]
An experimental method to locate the three-dimensional coordinates of the center of mass begins by supporting the object at three points and measuring the forces, F1, F2, and F3 that resist the weight of the object, 

or
This equation yields the coordinates of the center of mass R* in the horizontal plane as,
The center of mass lies on the vertical line L, given by
The three-dimensional coordinates of the center of mass are determined by performing this experiment twice with the object positioned so that these forces are measured for two different horizontal planes through the object. The center of mass will be the intersection of the two lines L1 and L2 obtained from the two experiments.
Applications[edit]
Engineering designs[edit]
Automotive applications[edit]
Engineers try to design a sports car so that its center of mass is lowered to make the car handle better, which is to say, maintain traction while executing relatively sharp turns.
The characteristic low profile of the U.S. military Humvee was designed in part to allow it to tilt farther than taller vehicles without rolling over, by ensuring its low center of mass stays over the space bounded by the four wheels even at angles far from the horizontal.
Aeronautics[edit]
The center of mass is an important point on an aircraft, which significantly affects the stability of the aircraft. To ensure the aircraft is stable enough to be safe to fly, the center of mass must fall within specified limits. If the center of mass is ahead of the forward limit, the aircraft will be less maneuverable, possibly to the point of being unable to rotate for takeoff or flare for landing.[19] If the center of mass is behind the aft limit, the aircraft will be more maneuverable, but also less stable, and possibly unstable enough so as to be impossible to fly. The moment arm of the elevator will also be reduced, which makes it more difficult to recover from a stalled condition.[20]
For helicopters in hover, the center of mass is always directly below the rotorhead. In forward flight, the center of mass will move forward to balance the negative pitch torque produced by applying cyclic control to propel the helicopter forward; consequently a cruising helicopter flies «nose-down» in level flight.[21]
Astronomy[edit]
The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the barycenter. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star, both bodies are actually orbiting a point that lies away from the center of the primary (larger) body.[22] For example, the Moon does not orbit the exact center of the Earth, but a point on a line between the center of the Earth and the Moon, approximately 1,710 km (1,062 miles) below the surface of the Earth, where their respective masses balance. This is the point about which the Earth and Moon orbit as they travel around the Sun. If the masses are more similar, e.g., Pluto and Charon, the barycenter will fall outside both bodies.
Rigging and safety[edit]
Knowing the location of the center of gravity when rigging is crucial, possibly resulting in severe injury or death if assumed incorrectly. A center of gravity that is at or above the lift point will most likely result in a tip-over incident. In general, the further the center of gravity below the pick point, the more safe the lift. There are other things to consider, such as shifting loads, strength of the load and mass, distance between pick points, and number of pick points. Specifically, when selecting lift points, it’s very important to place the center of gravity at the center and well below the lift points.[23]
Body motion[edit]
In kinesiology and biomechanics, the center of mass is an important parameter that assists people in understanding their human locomotion. Typically, a human’s center of mass is detected with one of two methods: the reaction board method is a static analysis that involves the person lying down on that instrument, and use of their static equilibrium equation to find their center of mass; the segmentation method relies on a mathematical solution based on the physical principle that the summation of the torques of individual body sections, relative to a specified axis, must equal the torque of the whole system that constitutes the body, measured relative to the same axis.[24]
See also[edit]
- Barycenter
- Buoyancy
- Center of mass (relativistic)
- Center of percussion
- Center of pressure (fluid mechanics)
- Center of pressure (terrestrial locomotion)
- Centroid
- Circumcenter of mass
- Expected value
- Mass point geometry
- Metacentric height
- Roll center
- Weight distribution
Notes[edit]
- ^ Shore 2008, pp. 9–11.
- ^ Baron 2004, pp. 91–94.
- ^ Baron 2004, pp. 94–96.
- ^ Baron 2004, pp. 96–101.
- ^ Baron 2004, pp. 101–106.
- ^ Mancosu 1999, pp. 56–61.
- ^ Erlichson, H. (1996). «Christiaan Huygens’ discovery of the center of oscillation formula». American Journal of Physics. 64 (5): 571–574. Bibcode:1996AmJPh..64..571E. doi:10.1119/1.18156. ISSN 0002-9505.
- ^ Walton 1855, p. 2.
- ^ Beatty 2006, p. 29.
- ^ Levi 2009, p. 85.
- ^ Bai & Breen 2008.
- ^ Kleppner & Kolenkow 1973, p. 117.
- ^ The Feynman Lectures on Physics Vol. I Ch. 19: Center of Mass; Moment of Inertia
- ^ Kleppner & Kolenkow 1973, pp. 119–120.
- ^ Feynman, Leighton & Sands 1963, pp. 19.1–19.2.
- ^ Hamill 2009, pp. 20–21.
- ^ «The theory and design of British shipbuilding». Amos Lowrey Ayre. p. 3. Retrieved 2012-08-20.
- ^ Sangwin 2006, p. 7.
- ^ Federal Aviation Administration 2007, p. 1.4.
- ^ Federal Aviation Administration 2007, p. 1.3.
- ^ «Helicopter Aerodynamics» (PDF). p. 82. Archived from the original (PDF) on 2012-03-24. Retrieved 2013-11-23.
- ^ Murray & Dermott 1999, pp. 45–47.
- ^ «Structural Collapse Technician: Module 4 — Lifting and Rigging» (PDF). FEMA.gov. Retrieved 2019-11-27.
- ^ Vint 2003, pp. 1–11.
References[edit]
- Asimov, Isaac (1988) [1966], Understanding Physics, Barnes & Noble Books, ISBN 978-0-88029-251-1
- Bai, Linge; Breen, David (2008). «Calculating Center of Mass in an Unbounded 2D Environment». Journal of Graphics, GPU, and Game Tools. 13 (4): 53–60. doi:10.1080/2151237X.2008.10129266. S2CID 40807367.
- Baron, Margaret E. (2004) [1969], The Origins of the Infinitesimal Calculus, Courier Dover Publications, ISBN 978-0-486-49544-6
- Beatty, Millard F. (2006), Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Mathematical Concepts and Methods in Science and Engineering, vol. 33, Springer, ISBN 978-0-387-23704-6
- De Silva, Clarence W. (2002), Vibration and shock handbook, CRC Press, ISBN 978-0-8493-1580-0
- Federal Aviation Administration (2007), Aircraft Weight and Balance Handbook (PDF), United States Government Printing Office, archived from the original (PDF) on 2011-10-19, retrieved 2011-10-23
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1963), The Feynman Lectures on Physics, vol. 1 (Sixth printing, February 1977 ed.), Addison-Wesley, ISBN 978-0-201-02010-6
- Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (1986), The Mechanical Universe: Mechanics and heat, advanced edition, Cambridge University Press, ISBN 978-0-521-30432-0
- Giambattista, Alan; Richardson, Betty McCarthy; Richardson, Robert Coleman (2007), College physics, vol. 1 (2nd ed.), McGraw-Hill Higher Education, ISBN 978-0-07-110608-5
- Goldstein, Herbert; Poole, Charles; Safko, John (2001), Classical Mechanics (3rd ed.), Addison Wesley, ISBN 978-0-201-65702-9
- Goldstein, Herbert; Poole, Charles; Safko, John (2002), Classical Mechanics (3rd ed.), Addison-Wesley, ISBN 978-0-201-65702-9
- Goodman, Lawrence E.; Warner, William H. (2001) [1964], Statics, Dover, ISBN 978-0-486-42005-9
- Hamill, Patrick (2009), Intermediate Dynamics, Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
- Jong, I. G.; Rogers, B. G. (1995), Engineering Mechanics: Statics, Saunders College Publishing, ISBN 978-0-03-026309-5
- Kleppner, Daniel; Kolenkow, Robert (1973), An Introduction to Mechanics (2nd ed.), McGraw-Hill, ISBN 978-0-07-035048-9
- Levi, Mark (2009), The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, ISBN 978-0-691-14020-9
- Mancosu, Paolo (1999), Philosophy of mathematics and mathematical practice in the seventeenth century, Oxford University Press, ISBN 978-0-19-513244-1
- Millikan, Robert Andrews (1902), Mechanics, molecular physics and heat: a twelve weeks’ college course, Chicago: Scott, Foresman and Company, retrieved 2011-05-25
- Murray, Carl; Dermott, Stanley (1999), Solar System Dynamics, Cambridge University Press, ISBN 978-0-521-57295-8
- O’Donnell, Peter J. (2015), Essential Dynamics and Relativity, CRC Press, ISBN 978-1-466-58839-4
- Pollard, David D.; Fletcher, Raymond C. (2005), Fundamentals of Structural Geology, Cambridge University Press, ISBN 978-0-521-83927-3
- Pytel, Andrew; Kiusalaas, Jaan (2010), Engineering Mechanics: Statics, vol. 1 (3rd ed.), Cengage Learning, ISBN 978-0-495-29559-4
- Rosen, Joe; Gothard, Lisa Quinn (2009), Encyclopedia of Physical Science, Infobase Publishing, ISBN 978-0-8160-7011-4
- Sangwin, Christopher J. (2006), «Locating the centre of mass by mechanical means» (PDF), Journal of the Oughtred Society, 15 (2), archived from the original (PDF) on 2011-10-05, retrieved 2011-10-23
- Serway, Raymond A.; Jewett, John W. (2006), Principles of physics: a calculus-based text, vol. 1 (4th ed.), Thomson Learning, Bibcode:2006ppcb.book…..J, ISBN 978-0-534-49143-7
- Shirley, James H.; Fairbridge, Rhodes Whitmore (1997), Encyclopedia of planetary sciences, Springer, ISBN 978-0-412-06951-2
- Shore, Steven N. (2008), Forces in Physics: A Historical Perspective, Greenwood Press, ISBN 978-0-313-33303-3
- Symon, Keith R. (1971), Mechanics (3rd ed.), Addison-Wesley, ISBN 978-0-201-07392-8
- Tipler, Paul A.; Mosca, Gene (2004), Physics for Scientists and Engineers, vol. 1A (5th ed.), W. H. Freeman and Company, ISBN 978-0-7167-0900-8
- Van Pelt, Michael (2005), Space Tourism: Adventures in Earth Orbit and Beyond, Springer, ISBN 978-0-387-40213-0
- Vint, Peter (2003), «LAB: Center of Mass (Center of Gravity) of the Human Body» (PDF), KIN 335 — Biomechanics, retrieved 2013-10-18
- Walton, William (1855), A collection of problems in illustration of the principles of theoretical mechanics (2nd ed.), Deighton, Bell & Co.
External links[edit]
Look up barycenter in Wiktionary, the free dictionary.
- Motion of the Center of Mass shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
- The Solar System’s barycenter, simulations showing the effect each planet contributes to the Solar System’s barycenter.
Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».
Оглавление:
- Общие сведения
- Связь с центром тяжести
- Вычисление положения
- Геометрический способ определения
Общие сведения
Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.
Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.
Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:
- центра масс;
- вращения.
Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.
Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.
Связь с центром тяжести
Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.
Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.
Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.
Для примера можно привести список однородных фигур с указанием их центральной точки:
- отрезок — середина;
- параллелограмм — место пересечения диагоналей;
- треугольник — точка пересечения медиан (центроид);
- любой правильный многоугольник — центр поворотной симметрии;
- полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.
Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.
Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.
При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.
Вычисление положения
Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.
На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.
Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.
Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.
Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.
При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.
Геометрический способ определения
Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.
Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.
Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.
Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.
Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.
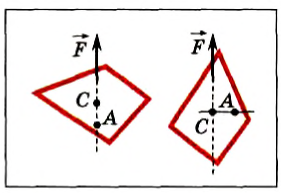
Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.
Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.
Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.