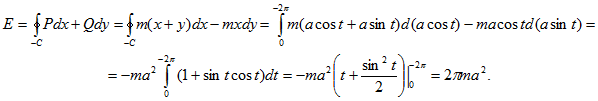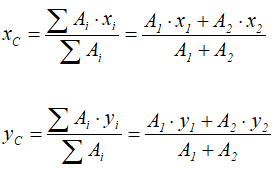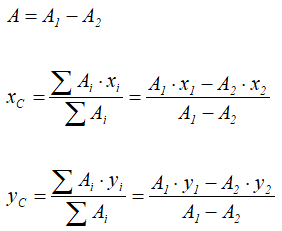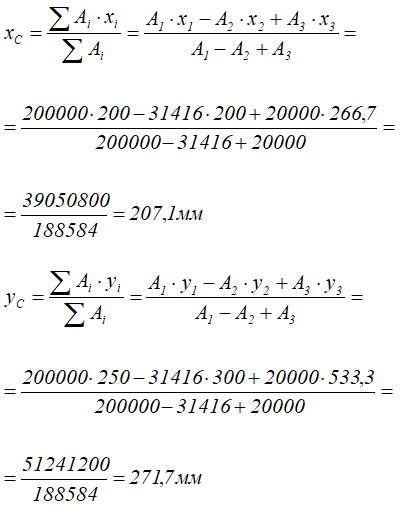Статические моменты и координаты центра тяжести
Вычисление статических моментов и координат центра тяжести кривой
а) Пусть материальная точка массы
отстоит от оси
на расстоянии
. Статическим моментом этой точки относительно оси
называют число
. Статическим моментом системы материальных точек
, расположенных по одну сторону от оси
, массы которых равны
, а расстояния от оси
равны
называют число
Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.
Поэтому если точки расположены на координатной плоскости,
, то
где — статический момент относительно оси
и
— относительно оси
.
б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой или по некоторой области
. Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.
Начнем со случая кривой линии , задаваемой уравнением
, причем предположим, что функция
непрерывна и неотрицательна.
Как обычно, разобьем отрезок на части точками
и обозначим через
и
наименьшее и наибольшее значения функции
на отрезке
, Этому разбиению соответствует разбиение дуги
на части
(рис. 60). Из физических соображений ясно, что статический момент
части
относительно оси абсцисс заключен между
и
, где
—длина этой части,
(напомним, что мы положили линейную плотность дуги равной единице). Таким образом,
. Поэтому
, то есть
Так как на отрезке выполняется неравенство
то в тех же границах, что и , заключен интеграл
. Значит,
(1)
Этот интеграл обозначают также следующим образом: или
.
Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» . Его статический момент равен
. А статический момент всей дуги равен сумме элементарных статических моментов, т. е.
. Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что
(2)
Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.
в) Введем понятие центра тяжести.
Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.
Обозначим через и
расстояния центра тяжести кривой от осей ординат и абсцисс.
Тогда, пользуясь определением центра тяжести кривой, получим:
Разрешая полученные равенства относительно и
, найдем координаты центра тяжести плоской кривой
Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.
Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.
Пример 1. Найти статический момент полуокружности относительно диаметра.
Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой
, где
— дифференциал дуги кривой
.
В выбранной системе координат уравнение полуокружности запишется так: . Тогда
и потому
.
Следовательно,
Пример 2. Найдем центр тяжести четверти окружности , расположенной в первом квадранте.
Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому . Достаточно найти только
.
Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:
Отсюда находим, что и
Поскольку длина четверти данной окружности равна
, то
Вычисление статических моментов и координат центров тяжести плоских фигур
Найдем статический момент прямоугольника со сторонами и
относительно стороны
. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны
и
(рис. 61). Масса элементарного прямоугольника равна его площади
(напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен
, а статический момент всего прямоугольника равен
(1)
Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой , где
— непрерывная и неотрицательная функция на отрезке
, снизу осью абсцисс, а с боков прямыми
.
Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота
. Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен
, а потому статический момент всей криволинейной трапеции равен
. В случае, когда не выполняется предположение о неотрицательности функции
, эту формулу надо заменить такой:
(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).
Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу , а потому ордината центра тяжести этой трапеции выражается формулой
Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен
, а статический момент всей трапеции выражается формулой
. Следовательно, абсцисса центра тяжести выражается так:
.
Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:
Решение. Так как параметр одной арки циклоиды изменяется от
до
, то
Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды
.
Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой , то центр тяжести лежит на этой прямой и, следовательно,
. Ордината
центра тяжести находится по формуле
.
Так как , то
.
Итак, центр тяжести данной фигуры находится в точке .
Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды .
Решение. Данная фигура расположена симметрично относительно прямой , следовательно, центр тяжести ее находится на этой прямой, и потому
. Найдем
по формуле
.
Площадь данной фигуры была вычислена раньше, она равна
. Следовательно,
Центр тяжести данной фигуры находится в точке .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
— координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
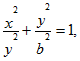
Переходим к параметрическим координатам эллипса Напомним, что
— фокусное расстояние эллипса, а
— эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 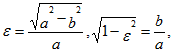
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
— обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
Пусть на плоскости Oxy дана
система материальных точек ,
, …,
с массами
координаты центра
тяжести в данном случае будут определяться по формулам

Центр
тяжести плоской линии
Пусть
задана кривая АВ уравнением ,
, и пусть эта кривая представляет собой материальную
линию.
Координаты центра
тяжести данной линии

Центр
тяжести плоской фигуры.
Пусть данная фигура,
ограниченная линиями ,
,
,
, представляет собой материальную плоскую фигуру.
Координаты центра
тяжести такой фигуры
Пример:
Вычислить
координаты центра масс однородной плоской фигуры, ограниченной линиями и
Координаты центра
тяжести такой фигуры
Данное значение координаты можно получить
из соображений симметрии.
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
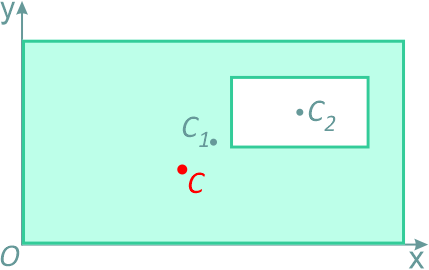
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
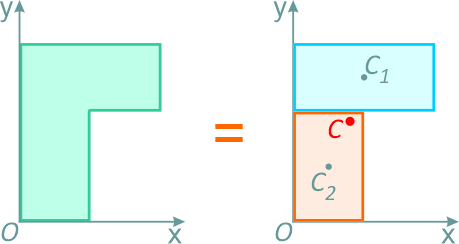
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
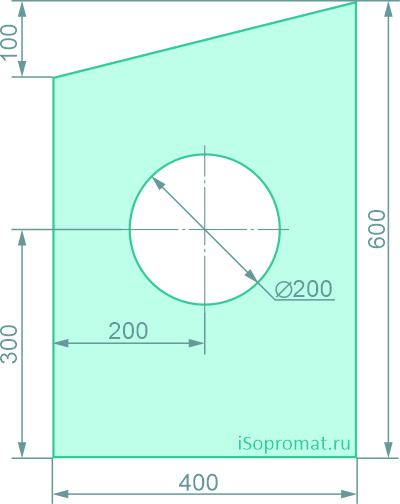
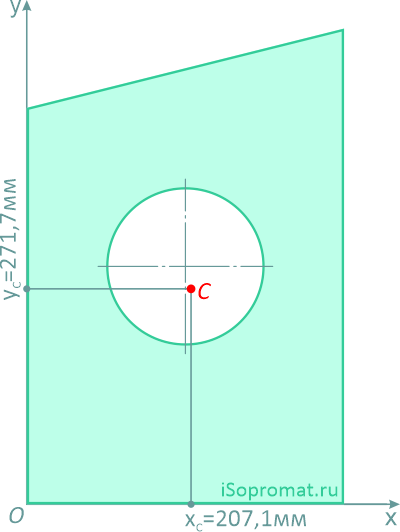
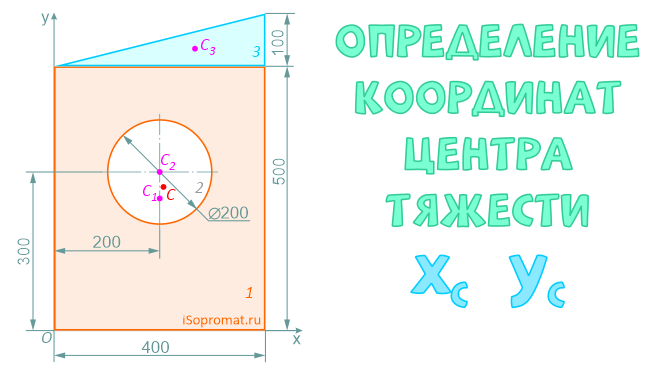
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
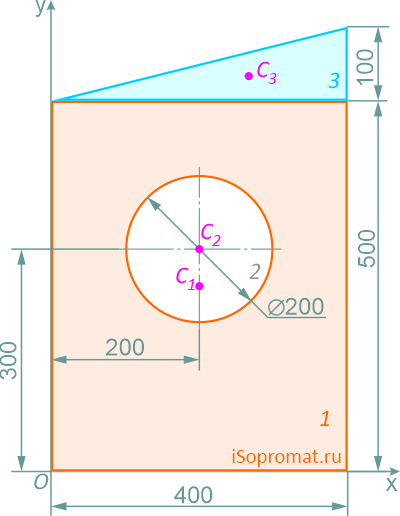
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
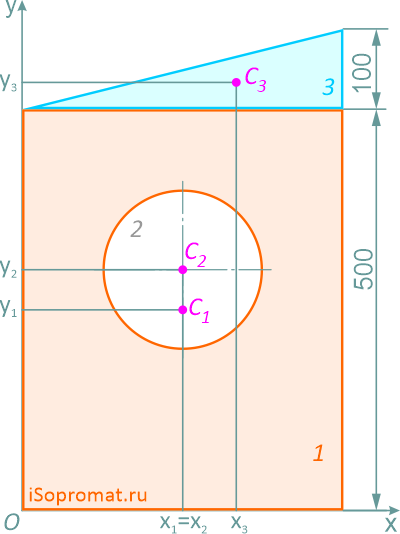
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Задача 1
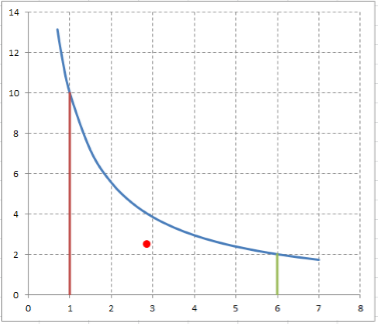
Найти координаты центра тяжести (КЦТ) материальной плоской фигуры в виде криволинейной трапеции (КрТ), образованной кривой $y=frac{150}{12cdot x+3} $ между точками с абсциссами $x=1$ и $x=6$. Поверхностную плотность фигуры считать величиной постоянной. Выполнить графические построения.
График данной криволинейной трапеции:
КЦТ материальной плоской фигуры в виде КрТ, образованной кривой $y=yleft(xright)$ на промежутке $left[a,; bright]$, вычисляют по формулам $x_{C} =frac{int limits _{a}^{b}xcdot yleft(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } $ и $y_{C} =frac{frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } $.
Продолжение задачи 1
Находим интеграл $I_{1} =int limits _{a}^{b}yleft(xright)cdot dx $:
[I_{1} =int limits _{1}^{6}frac{150}{12cdot x+3} cdot dx =frac{150}{12} cdot left[ln left|12cdot x+3right|right]_{1}^{6} =]
[=frac{150}{12} cdot left(ln left|12cdot 6+3right|-ln left|12cdot 1+3right|right)=]
[=12,5cdot left(ln 75-ln 15right)=12,5cdot ln frac{75}{15} =12,5cdot ln 5approx 12,5cdot 1,609approx 20,11; ]
Находим интеграл $I_{2} =frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx $:
[I_{2} =frac{1}{2} cdot int limits _{1}^{6}frac{150^{2} }{left(12cdot x+3right)^{2} } cdot dx =frac{150^{2} }{2} cdot int limits _{1}^{6}left(12cdot x+3right)^{-2} cdot dx =]
[=frac{150^{2} }{2cdot 12} cdot left[frac{left(12cdot x+3right)^{-2+1} }{-2+1} right]_{1}^{6} =-frac{150^{2} }{24} cdot left[frac{1}{12cdot x+3} right]_{1}^{6} =]
[=-frac{150^{2} }{24} cdot left(frac{1}{12cdot 6+3} -frac{1}{12cdot 1+3} right)=-frac{150^{2} }{24} cdot left(frac{1}{75} -frac{1}{15} right)=]
[=-frac{150^{2} }{24} cdot frac{1-5}{75} =frac{150^{2} }{24} cdot frac{4}{75} =frac{150^{2} }{6cdot 75} =50.]
Находим интеграл $I_{3} =int limits _{a}^{b}xcdot yleft(xright)cdot dx $:
[I_{3} =int limits _{1}^{6}xcdot frac{150}{12cdot x+3} cdot dx =int limits _{1}^{6}frac{150cdot x}{12cdot x+3} cdot dx =]
[=int limits _{1}^{6}frac{12cdot 150cdot x}{12cdot left(12cdot x+3right)} cdot dx =int limits _{1}^{6}frac{12cdot 150cdot x+150cdot 3-150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =]
[=int limits _{1}^{6}frac{150cdot left(12cdot x+3right)-150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =int limits _{1}^{6}frac{150cdot left(12cdot x+3right)}{12cdot left(12cdot x+3right)} cdot dx -]
[-int limits _{1}^{6}frac{150cdot 3}{12cdot left(12cdot x+3right)} cdot dx =frac{150}{12} cdot int limits _{1}^{6}dx -frac{3}{12} cdot int limits _{1}^{6}frac{150}{12cdot x+3} cdot dx =]
[=frac{150}{12} cdot left[xright]_{1}^{6} -frac{3}{12} cdot I_{1} approx 12,5cdot left(6-1right)-frac{3}{12} cdot 20,11approx 62,5-5,03approx 57,47.]
Вычисляем КЦТ:
[x_{C} =frac{int limits _{a}^{b}xcdot yleft(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } =frac{I_{3} }{I_{1} } approx frac{57,47}{20,11} approx 2,86;]
[y_{C} =frac{frac{1}{2} cdot int limits _{a}^{b}y^{2} left(xright)cdot dx }{int limits _{a}^{b}yleft(xright)cdot dx } =frac{I_{2} }{I_{1} } approx frac{50}{20,11} approx 2,49.]
Центр тяжести отмечен на рисунке красной точкой.
Задача 2
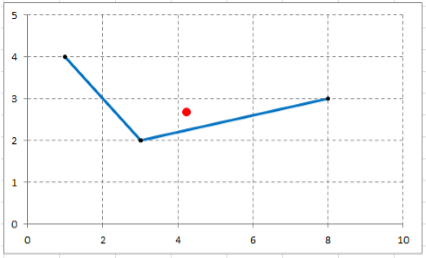
Найти КЦТ материальной кривой в виде ломаной линии, проходящей последовательно через заданные точки $Mleft(1,; 4right)$,~$Nleft(3,; 2right)$ и $Kleft(8,; 3right)$. Линейную плотность ломаной считать величиной постоянной. Выполнить графические построения.
График данной ломаной:
Формулы для вычисления КЦТ плоской кривой имеют вид $x_{C} =frac{int limits _{a}^{b}xcdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } $ и $y_{C} =frac{int limits _{a}^{b}yleft(xright)cdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } $.
Продолжение задачи 2
Находим уравнения прямых, учитывая, что общее уравнение прямой имеет следующий вид:
$Acdot x+Bcdot y+C=0$, где $A=y_{2} -y_{1} $, $B=x_{1} -x_{2} $, $C=-Acdot x_{1} -Bcdot y_{1} $.
- Для прямой $MN$ имеем такие значения коэффициентов:
- Для прямой $NK$ имеем такие значения коэффициентов:
[A=y_{2} -y_{1} =2-4=-2; B=x_{1} -x_{2} =1-3=-2;]
[C=-Acdot x_{1} -Bcdot y_{1} =2cdot 1+2cdot 4=10.]
Уравнение прямой $MN$: $-2cdot x-2cdot y+10=0$ или $-x-y+5=0$.
[A=y_{2} -y_{1} =3-2=1; B=x_{1} -x_{2} =3-8=-5; ]
[C=-Acdot x_{1} -Bcdot y_{1} =-1cdot 3+5cdot 2=7.]
Уравнение прямой $NK$: $x-5cdot y+7=0$.
Находим выражение $sqrt{1+y’^{2} } $ для данных прямых:
- для прямой $MN$ $y=-x+5$, $y’=-1$, $sqrt{1+y’^{2} } =sqrt{2} approx 1,41$.
- для прямой $NK$ $y=frac{1}{5} cdot x+frac{7}{5} $, $y’=frac{1}{5} $, $sqrt{1+y’^{2} } =frac{sqrt{26} }{5} approx 1,02$.
Находим интеграл $I_{1} =int limits _{a}^{b}xcdot sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:
[I_{1} =1,41cdot int limits _{1}^{3}xcdot dx +1,02cdot int limits _{3}^{8}xcdot dx =1,41cdot left[frac{x^{2} }{2} right]_{1}^{3} +1,02cdot left[frac{x^{2} }{2} right]_{3}^{8} =]
[=frac{1,41}{2} cdot left(3^{2} -1^{2} right)+frac{1,02}{2} cdot left(8^{2} -3^{2} right)=frac{1,41}{2} cdot 8+frac{1,02}{2} cdot 55approx 33,69.]
Находим интеграл $I_{2} =int limits _{a}^{b}ycdot sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:
[I_{2} =1,41cdot int limits _{1}^{3}left(-x+5right)cdot dx +1,02cdot int limits _{3}^{8}left(frac{1}{5} cdot x+frac{7}{5} right)cdot dx =]
[=1,41cdot left[-frac{x^{2} }{2} +5cdot xright]_{1}^{3} +1,02cdot left[frac{1}{5} cdot frac{x^{2} }{2} +frac{7}{5} cdot xright]_{3}^{8} =1,41cdot 6+1,02cdot frac{125}{10} approx 21,21.]
Находим интеграл $I_{3} =int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx $ вдоль всей ломаной:
[I_{3} =1,41cdot int limits _{1}^{3}dx +1,02cdot int limits _{3}^{8}dx =1,41cdot 2+1,02cdot 5approx 7,92.]
Находим КЦТ ломаной линии:
[x_{C} =frac{int limits _{a}^{b}xcdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } =frac{I_{1} }{I_{3} } approx frac{33,69}{7,92} approx 4,25; ]
[y_{C} =frac{int limits _{a}^{b}yleft(xright)cdot sqrt{1+y’^{2} left(xright)} cdot dx }{int limits _{a}^{b}sqrt{1+y’^{2} left(xright)} cdot dx } =frac{I_{2} }{I_{3} } approx frac{21,21}{7,92} approx 2,68.]
Центр тяжести отмечен на рисунке красной точкой.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

.gif)
.gif)
.gif)
.gif)
.gif)
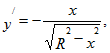
.gif)
.gif)
.gif)
.gif)
.gif)
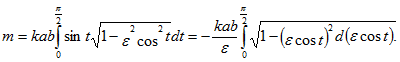
.gif)
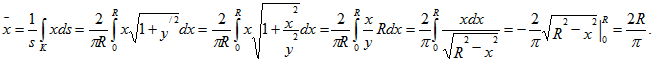
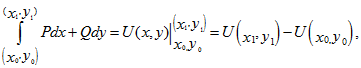
.gif)
.gif)
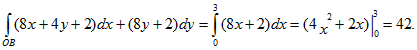
.gif)
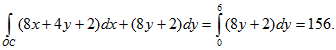
.gif)
.gif)
.gif)
.gif)
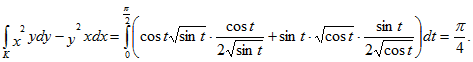
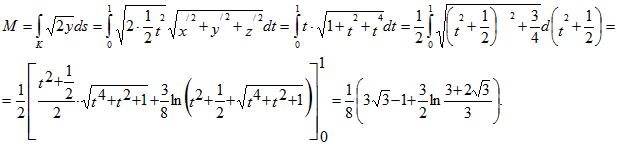
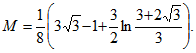
.gif)
.gif)
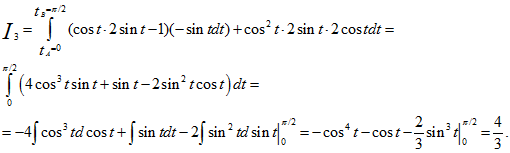
.gif)
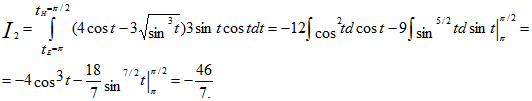
.gif)
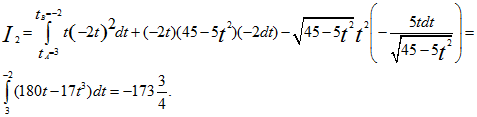
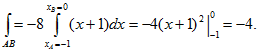
.gif)
.gif)
.gif)
.gif)
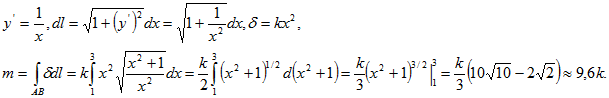
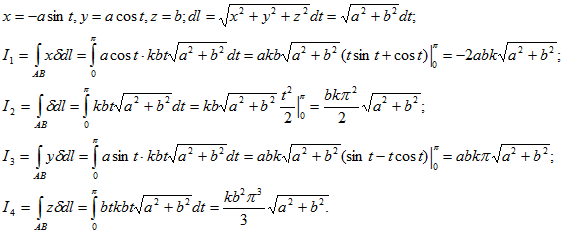
.gif)