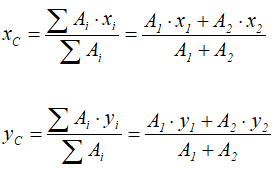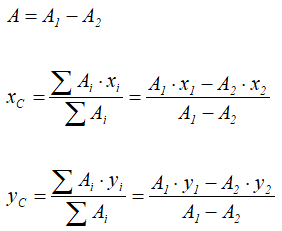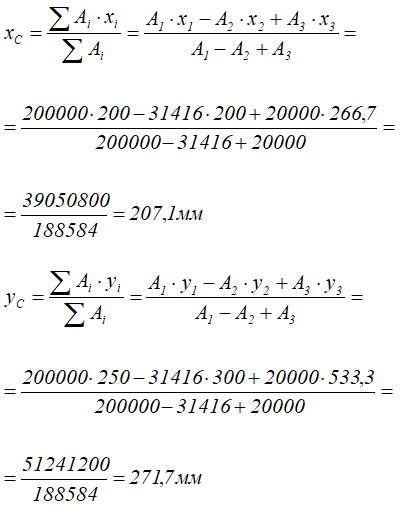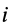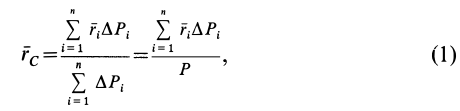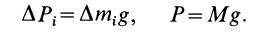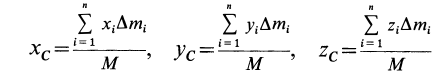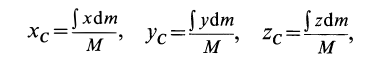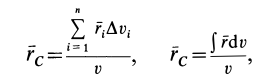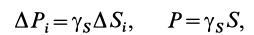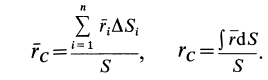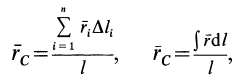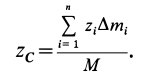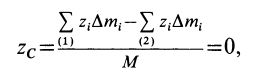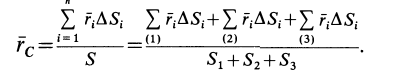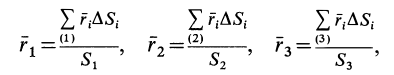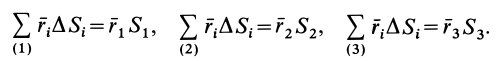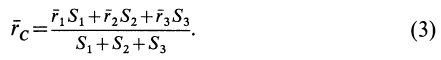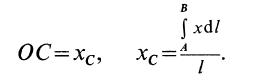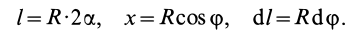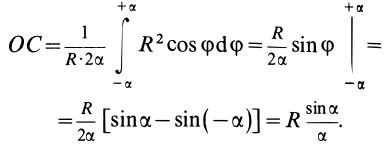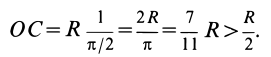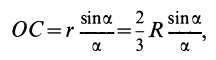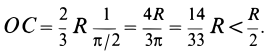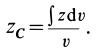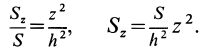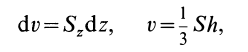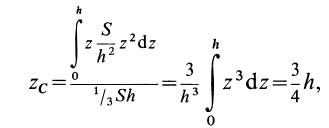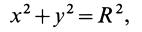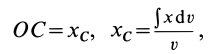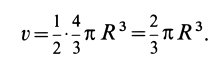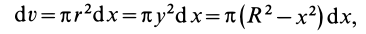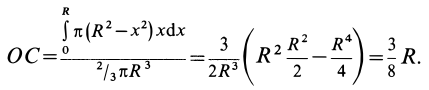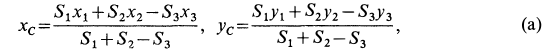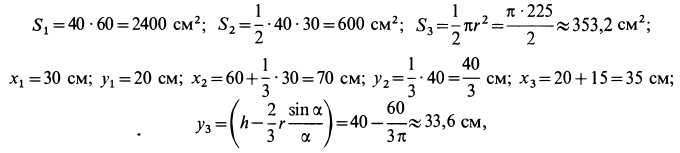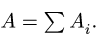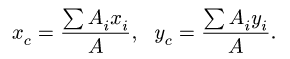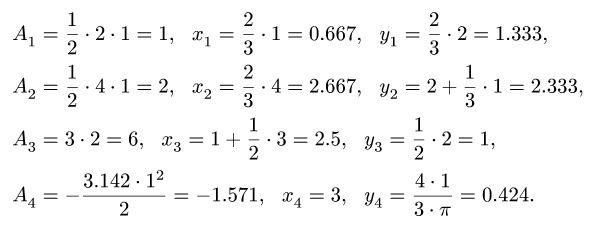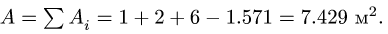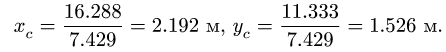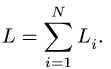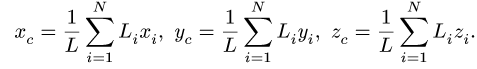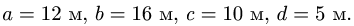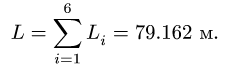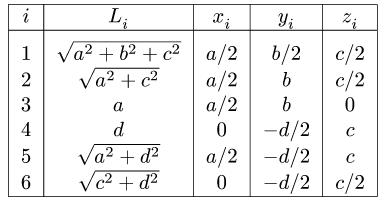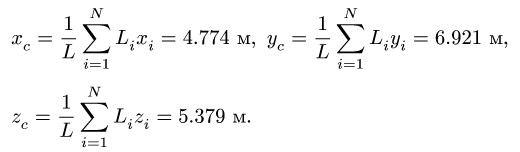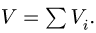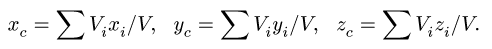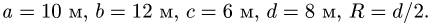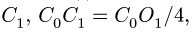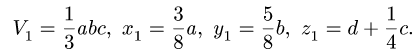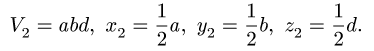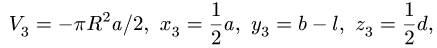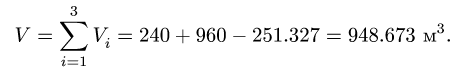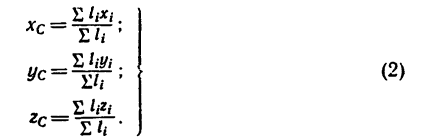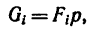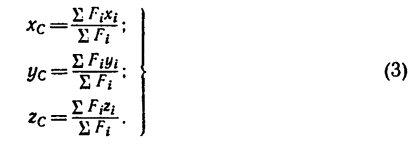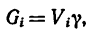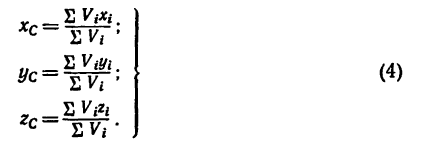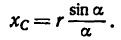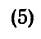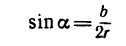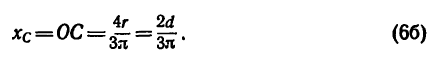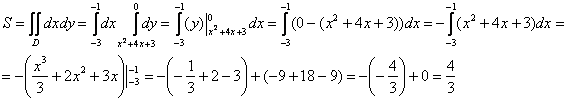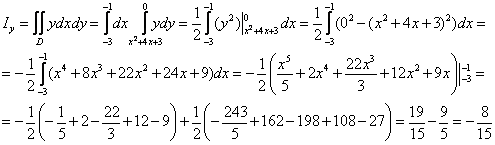
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
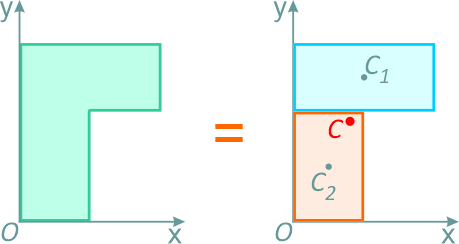
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
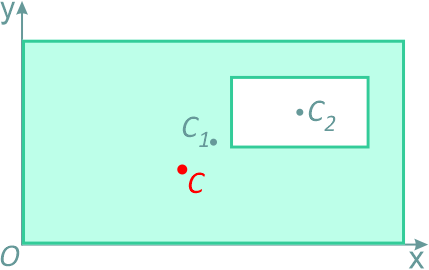
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
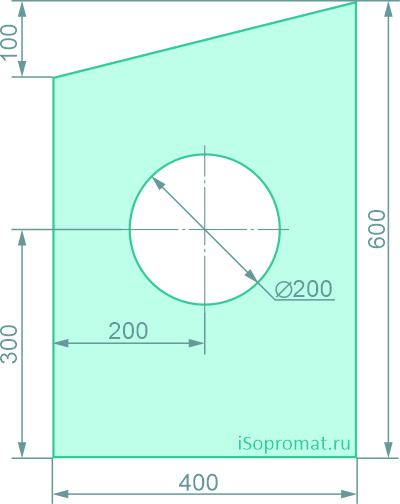
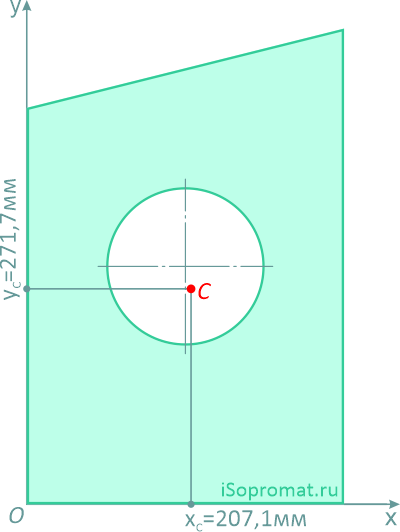
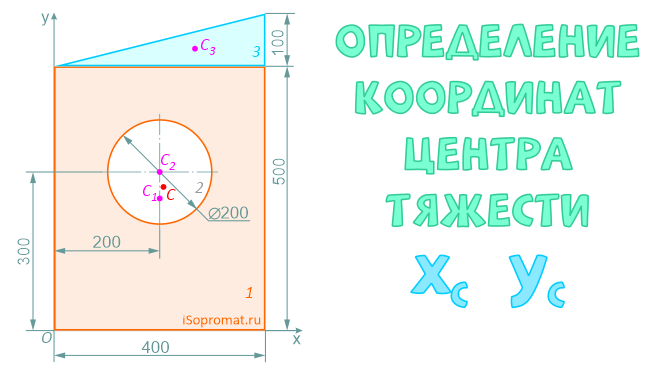
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
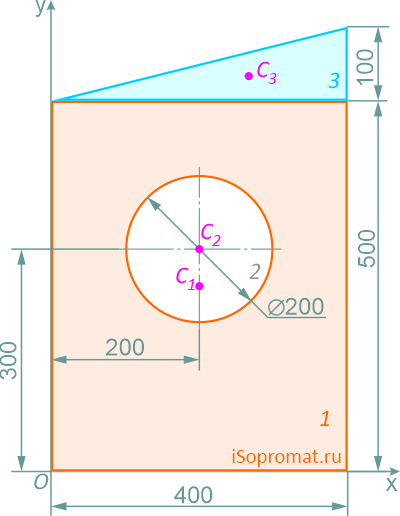
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
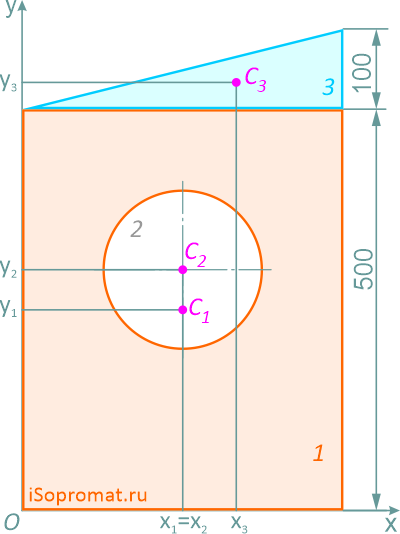
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
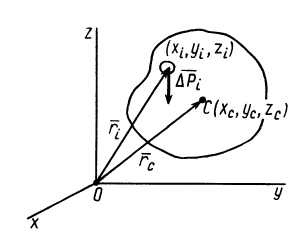
Радиус-вектор центра тяжести тела 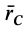
где 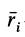

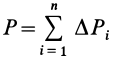

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

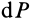
где 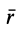
где 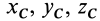
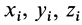
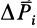
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 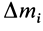
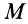

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
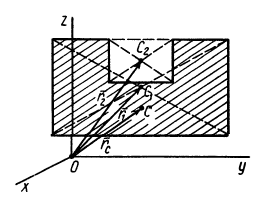
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 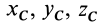
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 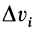


где 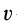


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 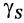
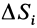
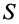
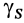
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 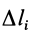
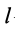
Методы определения центров тяжести (Центров масс)
Метод симметрии
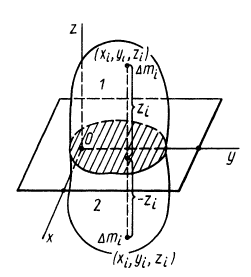
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 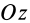
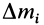
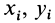
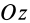
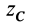
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 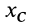
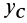
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
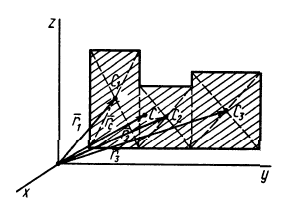
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 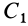
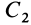
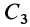
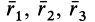
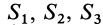
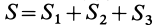
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 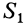
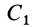
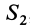
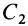
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
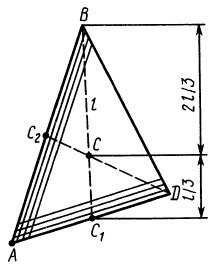
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 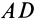

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
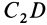

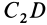
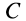

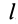
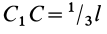
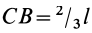
Рис. 92
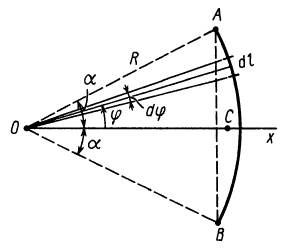
Дуга окружности
Дуга окружности 
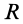
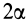
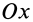

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 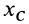
Таким образом,
Для полуокружности 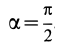
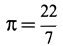
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 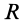
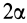
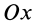
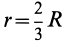
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 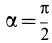
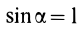
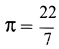
Объем пирамиды и конуса
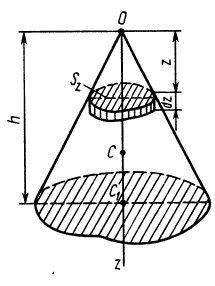
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 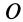
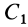
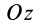
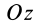
Разобьем конус плоскостями, перпендикулярными оси 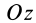
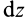
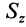
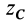
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 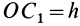
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 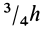
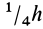
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 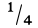
Объем полушара
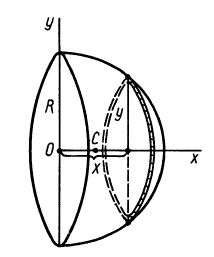
Полушар имеет ось симметрии, которую примем за координатную ось 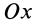
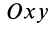
где 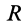
где 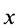
Объем элементарного диска
так как радиус диска 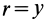
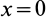
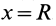
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
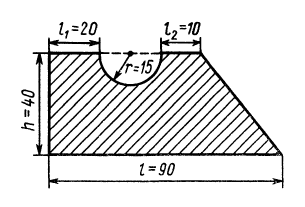
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
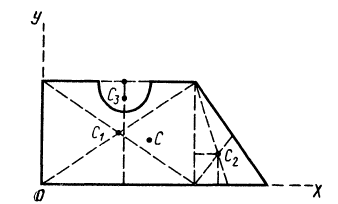
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 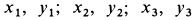
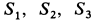
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 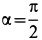
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 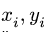
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
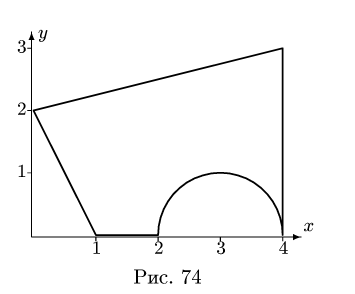
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
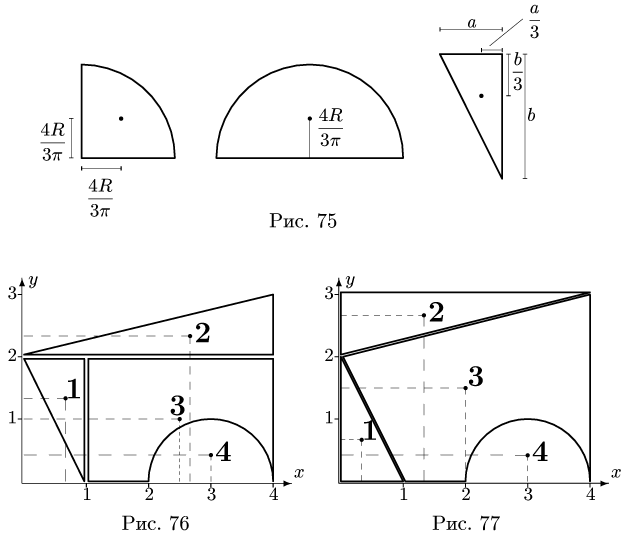
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 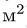
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
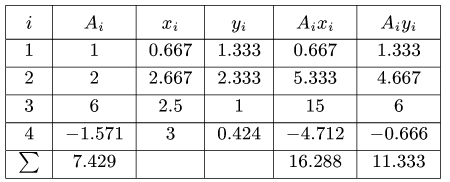
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 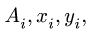
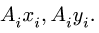
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 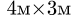
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 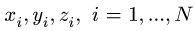
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
Задача №3
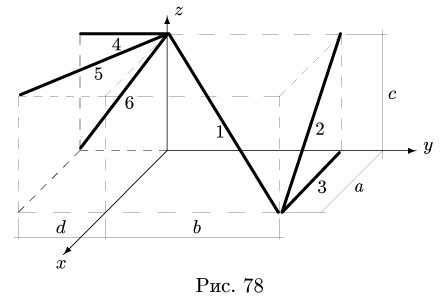
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 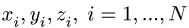
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 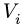
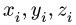
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
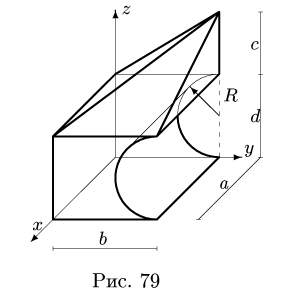
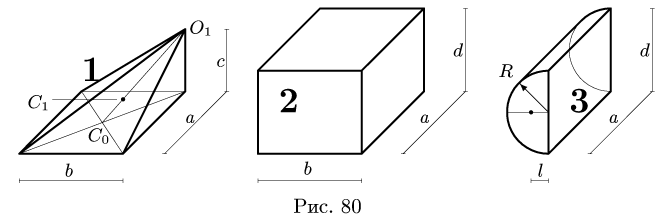
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 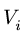
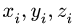
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 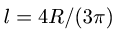
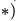
3. Находим общий объем тела:
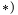
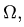
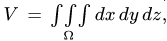
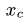
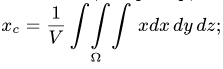
4. Определяем координаты центра тяжести тела:
Центр тяжести
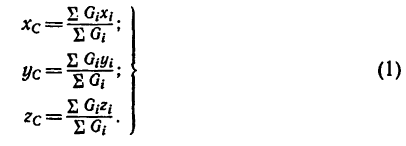
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
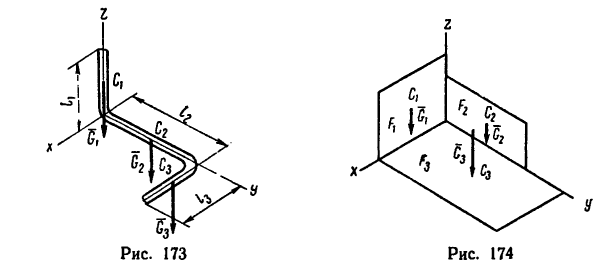
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 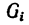
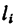
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 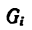
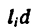
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 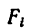
После подстановки этого значения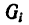
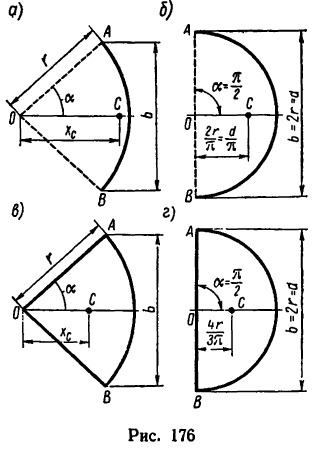
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 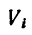
После подстановки значений 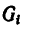
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
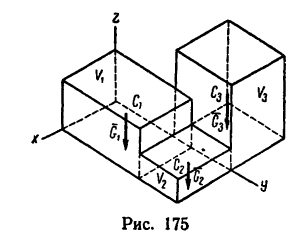
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 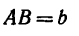
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
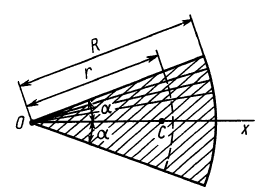
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
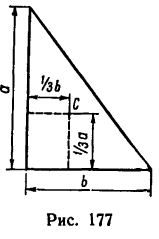
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
1.6. Центр тяжести плоской фигуры
Это популярное физическое приложение двойного интеграла.
О центре тяжести плоской фигуры я рассказывал ещё в курсе аналитической геометрии, и сейчас мы на пальцах
повторим, что это такое. Вырежьте из тонкого куска картона произвольную фигуру, какую захотИте. …Есть? Поднимите указательный
палец строго вверх J. Теперь положите картонку на палец и добейтесь того, чтобы она не сваливалась. Эта точка картонной
фигуры – и есть её центр тяжести.
В студенческой практике для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура,
то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная чугунные игрушки, тяжёлое детство и т.д.
Далее по умолчанию речь пойдёт только о таких фигурах.
Первое правило и простейший пример: если у плоской фигуры есть центр симметрии, то он является
центром тяжести данной фигуры. Например, центр круглой или квадратной однородной пластины. Логично и по-житейски
понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра.
Однако в суровых реалиях вам вряд ли подкинут такую халяву, и поэтому на помощь придётся привлечь серьёзный математический
аппарат:
Координаты центра тяжести
плоской однородной ограниченной фигуры
рассчитываются по
следующим формулам:
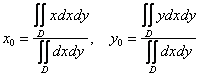
записать так:
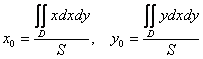
– площадь фигуры (области
).
И наиболее компактная запись:
, где
Интеграл будем
условно называть «иксовым» интегралом, а интеграл – «игрековым» интегралом.
Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией , формулы более
сложные:
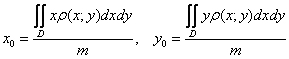
– масса фигуры;
в случае однородной плотности фигуры эти формулы упрощаются до вышеприведённых формул.
На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы, кстати, сейчас предоставляется прекрасная возможность
потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела: …или есть? 
Пример 29
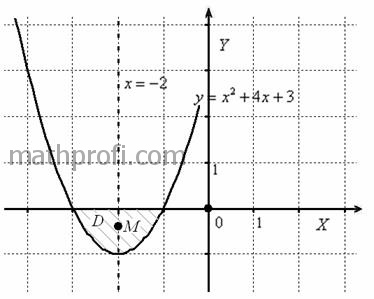
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями .
Решение: линии здесь элементарны: задаёт ось абсцисс, а уравнение
– банальную параболу. Я выполню сразу весь чертёж с
готовой точкой центра тяжести фигуры:
Правило второе: если у фигуры существует ось симметрии, то центр тяжести данной фигуры
обязательно лежит на этой оси.
В нашем случае фигура симметрична относительно прямой (проведена пунктиром), то есть фактически мы уже знаем
«иксовую» координату точки «эм».
Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна.
Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» – это
поможет проверить полученные значения на предмет явных ошибок.
…Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и
мысленно поставьте на него заштрихованную «подошву» точкой . Теоретически фигура не должна упасть.
Координаты центра тяжести фигуры найдём по формулам , где
.
Порядок обхода области (фигуры) здесь очевиден:
Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех двойных интегралов! А их тут будет три штуки:
1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить «одной строкой», главное,
не запутаться в вычислениях:
Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.
2) Иксовая координата центра тяжести уже найдена «графическим методом», поэтому можно
сослаться на симметрию и перейти к следующему пункту. Но делать так-таки не советую – велика вероятность, что вас заставят
решать по формуле.
В этой связи координату лучше рассчитать формально. Вычислим «иксовый» интеграл:
Таким образом: 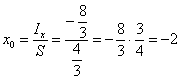
3) Найдём ординату центра тяжести. Вычислим «игрековый» интеграл, внутри
используем правило умножения
многочленов:
В результате: 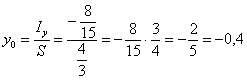
очень и очень похоже на правду. На заключительном этапе отмечаем на чертеже точку и записываем
Ответ:
Заметьте, что по условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру.
Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.
Следующие два примера для самостоятельного решения.
Попроще:
Пример 30
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями
И посложнее:
Пример 31
Найти центр тяжести однородной плоской фигуры, ограниченной линиями . Фигуру и её центр тяжести изобразить на чертеже.
И это как раз тот случай, когда вроде бы выполнены предпосылки для перехода к полярной
системе координат, но в результате получаются настолько харкордные интегралы, что уж лучше решать в декартовых
координатах.
Примерные образцы решений в конце книги.
Но, разумеется, есть задачи, где решение в полярных координатах оправдано. Желающие могут в качестве тренировки найти
центр тяжести фигуры из Примера 23, тем более, там уже найдена площадь. Верный ответ . С подробным решением этого, а также более сложных
примеров можно ознакомиться в соответствующей статье
сайта.
Ну а сейчас пришло время немного отдохнуть и повысить ставки:


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Статические моменты и координаты центра тяжести
Вычисление статических моментов и координат центра тяжести кривой
а) Пусть материальная точка массы
отстоит от оси
на расстоянии
. Статическим моментом этой точки относительно оси
называют число
. Статическим моментом системы материальных точек
, расположенных по одну сторону от оси
, массы которых равны
, а расстояния от оси
равны
называют число
Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.
Поэтому если точки расположены на координатной плоскости,
, то
где — статический момент относительно оси
и
— относительно оси
.
б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой или по некоторой области
. Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.
Начнем со случая кривой линии , задаваемой уравнением
, причем предположим, что функция
непрерывна и неотрицательна.
Как обычно, разобьем отрезок на части точками
и обозначим через
и
наименьшее и наибольшее значения функции
на отрезке
, Этому разбиению соответствует разбиение дуги
на части
(рис. 60). Из физических соображений ясно, что статический момент
части
относительно оси абсцисс заключен между
и
, где
—длина этой части,
(напомним, что мы положили линейную плотность дуги равной единице). Таким образом,
. Поэтому
, то есть
Так как на отрезке выполняется неравенство
то в тех же границах, что и , заключен интеграл
. Значит,
(1)
Этот интеграл обозначают также следующим образом: или
.
Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» . Его статический момент равен
. А статический момент всей дуги равен сумме элементарных статических моментов, т. е.
. Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что
(2)
Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.
в) Введем понятие центра тяжести.
Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.
Обозначим через и
расстояния центра тяжести кривой от осей ординат и абсцисс.
Тогда, пользуясь определением центра тяжести кривой, получим:
Разрешая полученные равенства относительно и
, найдем координаты центра тяжести плоской кривой
Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.
Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.
Пример 1. Найти статический момент полуокружности относительно диаметра.
Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой
, где
— дифференциал дуги кривой
.
В выбранной системе координат уравнение полуокружности запишется так: . Тогда
и потому
.
Следовательно,
Пример 2. Найдем центр тяжести четверти окружности , расположенной в первом квадранте.
Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому . Достаточно найти только
.
Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:
Отсюда находим, что и
Поскольку длина четверти данной окружности равна
, то
Вычисление статических моментов и координат центров тяжести плоских фигур
Найдем статический момент прямоугольника со сторонами и
относительно стороны
. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны
и
(рис. 61). Масса элементарного прямоугольника равна его площади
(напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен
, а статический момент всего прямоугольника равен
(1)
Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой , где
— непрерывная и неотрицательная функция на отрезке
, снизу осью абсцисс, а с боков прямыми
.
Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота
. Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен
, а потому статический момент всей криволинейной трапеции равен
. В случае, когда не выполняется предположение о неотрицательности функции
, эту формулу надо заменить такой:
(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).
Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу , а потому ордината центра тяжести этой трапеции выражается формулой
Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен
, а статический момент всей трапеции выражается формулой
. Следовательно, абсцисса центра тяжести выражается так:
.
Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:
Решение. Так как параметр одной арки циклоиды изменяется от
до
, то
Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды
.
Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой , то центр тяжести лежит на этой прямой и, следовательно,
. Ордината
центра тяжести находится по формуле
.
Так как , то
.
Итак, центр тяжести данной фигуры находится в точке .
Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды .
Решение. Данная фигура расположена симметрично относительно прямой , следовательно, центр тяжести ее находится на этой прямой, и потому
. Найдем
по формуле
.
Площадь данной фигуры была вычислена раньше, она равна
. Следовательно,
Центр тяжести данной фигуры находится в точке .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение центра тяжести плоской фигуры
Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.
При определении координат центра тяжести используются следующие методы:
1) метод симметрии: если сечение имеет центр симметрии или ось симметрии, то центр тяжести находится в центре симметрии или на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых, легко определить;
3) метод отрицательных площадей: этот способ является частным случаем способа разделения. Он используется, когда сечение имеет вырезы, срезы, полости (отверстия), которые рассматриваются как часть сечения с отрицательной площадью.
При решении задач на определение центра тяжести сложных сечений следует придерживаться следующего порядка:
1. Выбрать метод, который наиболее применим к данной задаче.
2. Разбить сложное сечение на простые части, для которых центры тяжести известны.
3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.
4. Определить координаты центров тяжести отдельных частей относительно выбранных осей.
5. Используя формулы определить искомые координаты центра тяжести заданного сечения.

где А1, А2 … Аn — площади простых сечений;
x1, x2 … xn, y1, y2 … yn– координаты центра тяжести простых сечений.
Координаты центра тяжести сложной плоской фигуры определяются после разделения ее на простые фигуры и определения их центров тяжести.
Координаты центра тяжести некоторых простых плоских фигур:
Порядок выполнения задания:
1) начертить заданное сложное сечение (фигуру), выбрать оси координат.
2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны;
3) определить необходимые данные для простых сечений:
4)определить координаты центров тяжести простых сечений относительно выбранных осей координат;
5) определить положение центра тяжести сложного сечения.
Найти координаты центра тяжести плоской фигуры, изображенной на рисунке.
Выбираем оси координат так, чтобы нижний и левый край фигуры совпали с ними:
Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3).
Вычисляем площади этих фигур:
S1 = 10·20 = 200; S2 = 0,5·5·10 = 25; S3 = π·9 =28,3.
Определяем координаты центров тяжести фигур:
x1 = 10; y1 = 5.
x2 = 5; y2 = 11,7.
x3= 5; y3= 5.
Координаты центра тяжести всей плоской фигуры: