Определение координаты движущегося тела

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Где:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
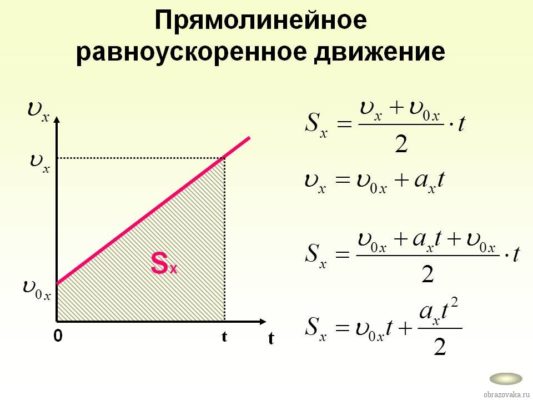
Как найти путь при равноускоренном движении?
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
План урока:
Механическое движение. Система отсчёта. Закон относительности движения
Уравнения движения. Радиус-вектор. Проекция вектора
Траектория. Путь. Перемещение
Равномерное прямолинейное движение: скорость и уравнение движения
Механическое движение. Система отсчёта. Закон относительности движения
Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.
То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).
Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.
Рисунок 1 – Иллюстрация к примеру
Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.
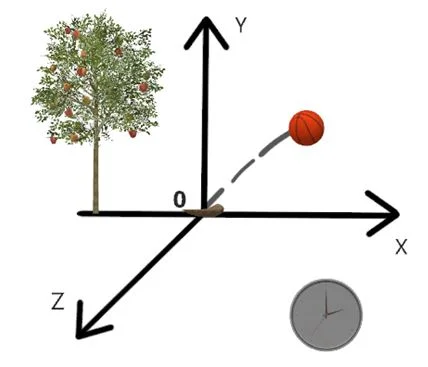
Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.
Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)
Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.
Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.
Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.
Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.
Уравнения движения. Радиус-вектор. Проекция вектора
Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?
Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:
Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.
Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.
В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).
Еще один способ описания движения – векторный.
*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»
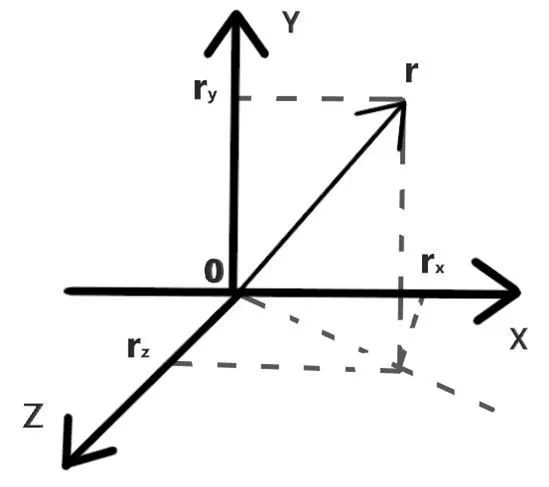
Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).
Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r1 и r2* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)
Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:
r = r(t)
Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.
Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.
*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.
Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).
Рисунок 4 – Построение проекции вектора на ось
Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.
Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.
Напоминания из геометрии:
-
два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;
-
проекции равных векторов равны.
Рассмотрим пример (см. рисунок 5)
Рисунок 5 – Задача на нахождение проекции векторов
Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.
Итак, вектор а: его начала соответствует координате хн=1, а конец хк = 4. Значит ax = хк – хн = 4-1 = 3. Вектор b: его начало лежит в точке хн=2, а конец хк =0. Значит bx = хк – хн = 0-2 = -2.
В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.
Иногда еще нужно находить составляющие компоненты вектора ах и ау. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).
Сумма векторов ах и ау равна а. Модули векторов ах и ау численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.
Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:
ах = а*cos(β);
аy = а*sin(β).
Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины ах и ау совпадали бы с координатами тела по осям ОХ и ОY.
Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.
Рисунок 6 – Нахождение компонент вектора а
Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.
Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве
В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.
Точки, в которые попал перпендикуляры к осям – rx, ry, rz – это и есть координаты x, y, z тела в текущий момент времени.
Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.
Рисунок 8 – Построение проекций радиус-вектора
Траектория. Путь. Перемещение
Траектория – это линия, вдоль которой движется тело.
Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.
Путь (S), пройденный телом, равен длине траектории.
Перемещение (r)* – это вектор, проведенный из начала пути в конец.
В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.
Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении
*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.
Равномерное прямолинейное движение: скорость и уравнение движения
Путь и перемещение при равномерном прямолинейном движении
Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.
Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:
- равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.
Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.
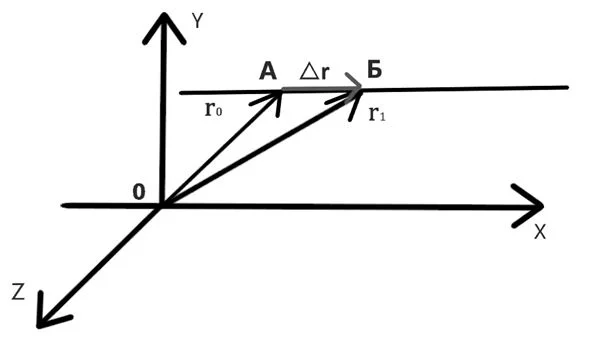
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r0, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении
Тогда скорость движения (v) будет вычисляться по формуле:
Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.
Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r1 — r0. Тогда выражение для скорости можно переписать в виде:
Из этого выражения следует:
r1 = r0 + v*t.
Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:
r = r0 + v*t.
Данное уравнение является уравнением движения при прямолинейном равномерном движении.
*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t1, где t – конечный момент времени, t1 – начальный. Если же начальный момент времени совпадает с началом отсчета t1 = 0, то △t = t – 0 = t.
Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.
Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
В этих выражениях r0x, r0y, r0z и vx, vy, vz – это компоненты изначальных векторов r0 и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.
В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х0) и конечной (х1) точки на ось ОХ.
Рисунок 9 – Перемещение тела в координатном представлении
Уравнение координаты (х) движения будет выглядеть:
x(t) = x0 + v*t.
А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:
S(t) = S0 + v*t.
Если точка начала двигаться из начала отсчета S0 = 0, можно переписать эту формулу в виде:
S(t) = v*t.
Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:
Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x0 = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.
Итак, для начала приведем все единицы измерения к СИ:
x0 = 3 см = 0,03 м.
Теперь можно записывать уравнение для координаты х:
x(t) = x0 + v*t = 0,03 + 5*t.
Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:
x(2) = 0,03 + 5*2 = 10, 03.
А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:
S = x(2) – x0 = 10, 03 – 0,03 = 10 м.
А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?
Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:
x(t) = x0 — v*t = 0,03 — 5*t.
Содержание:
- калькулятор координаты тела при равномерном прямолинейном движении
- формула координаты тела при равномерном прямолинейном движении
Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.
Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:
Формула координаты тела при равномерном прямолинейном движении
x=x_0+ V cdot t
x0 — начальная координата тела
V — скорость тела
t — время движения
x — координата тела в текущий момент времени (в момент времени t)
Таким образом, для того, чтобы найти координату тела при равномерном прямолинейном движении необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат.
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
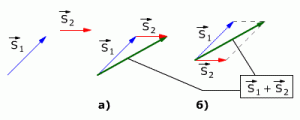
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
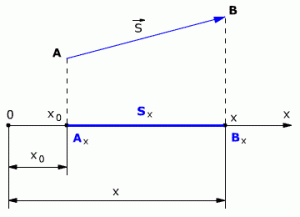
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения (см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
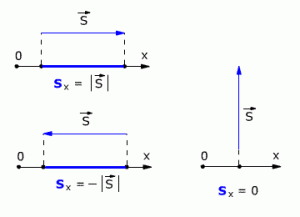
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
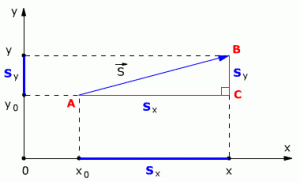
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Как определить координаты тела
Рассматривая движение тела в пространстве, описывают изменение во времени его координат, скорости, ускорения и других параметров. Обычно вводят декартову прямоугольную систему координат.

Инструкция
Если тело находится в покое и задана неподвижная система отсчета, его координаты в ней постоянны, с течением времени не меняются. Условное определение координат здесь зависит лишь выбора от нулевой точки и единиц измерения. График координат на осях «координаты-время» будет прямой, параллельной временной оси.
Если тело движется прямолинейно и равномерно, формула для его координат будет иметь вид: x=x0+v•t, где x0 – координата в начальный момент времени t=0, v – постоянная скорость. График координат будет представлен прямой линией, где скорость v – тангенс угла наклона.
Если же тело движется по прямой равноускоренно, то x=x0+v0•t+a•t²/2. Здесь x0 – начальная координата, v0 – начальная скорость, a – постоянное ускорение. Линейную зависимость в этом случае имеет скорость: v=v0+a•t, график скорости – прямая. А вот график для координат будет похож на параболу.
Скорость – первая производная координаты по времени. Если задана функция зависимости скорости от времени и начальные условия, можно установить и зависимость координат. Для этого уравнение скорости нужно проинтегрировать, а для поиска интегральной константы подставить дополнительно известные величины.
Пример. Скорость тела зависит от времени и имеет формулу v(t)=4t. В начальный момент времени тело имело координату x0. Найдите, как координаты изменяются в зависимости от времени.
Решение. Поскольку v=dx/dt, то dx/dt=4t. Теперь нужно разделить переменные. Для этого перенесите дифференциал времени dt в правую часть равенства: dx=4t·dt. Всё, можно интегрировать: ∫dx=∫4t·dt. Можно воспользоваться таблицей простейших интегралов, которая есть в конце многих задачников по физике. Итак, x=2t²+C, где C – константа.
Для поиска константы обратитесь к заданным начальным условиям. В задаче сказано, что в начальный момент времени тело имело координату x0. Это означает, что x=x0 при t=0. Подставьте эти данные в полученную формулу для координаты: x0=0+C, отсюда C=x0. Константа найдена, теперь можно подставить ее в функцию x=2t²+C: x=2t²+x0.Ответ. Координата тела зависит от времени как x=2t²+x0.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.