Определение прямоугольных координат по топографической карте.
Прямоугольные
координаты определяют с помощью
координатной (километровой) сетки,
представляющей собой сеть линий,
параллельных экватору и осевому меридиану
зоны.
Для
определения прямоугольных координат
заданной точки (рис. 4) сначала нужно
найти координаты левого нижнего угла
квадрата, образованного линиями
километровой сетки, в котором расположена
точка. Т.е. X0
и Y0,
записанные в метрах.

Рис.
4. Определение прямоугольных координат.
Далее
необходимо из заданной точки опустить
перпендикуляры к левой и нижней линиям
километровой сетки, измерить с помощью
циркуля-измерителя длины отрезков и
перевести, используя численный масштаб,
в метры на местности. Получим приращения
прямоугольных координат ∆x
и ∆y.
Искомые
абсцисса и ординаты рассчитываются по
формулам:
X
= X0
+ ∆x
Y
= Y0
+ ∆y.
Полярные координаты.
Для
решения многих задач применяют полярные
координаты, когда положение заданной
точки относительной нулевой (полюса)
определяется углом
направления
между полярной осью и радиусом-вектором
и длиной
радиуса-вектора.
Единицы измерения, таким образом,
смешанные – градусы и метры.
В
качестве полярной оси может быть выбрано
любая линия: геодезический или магнитный
меридиан, произвольное направление, но
при работе с топографическими картами
чаще всего используются вертикальный
линии километровой сетки, т.е. линии,
параллельные оси Х. Угол, отсчитываемый
по часовой стрелке от северного
направления линии параллельной оси
абсцисс, проходящей через исходную
точку, до направления на искомую точку,
называется дирекционным
углом α.
Ориентирующие углы.
Кроме
дирекционного угла определить положения
заданного двумя точками направления
можно с помощью геодезического и
магнитного азимутов.
Геодезический
азимут
Аг
– угол, отсчитываемый по часовой стрелке
от северного направления геодезического
меридиана, проходящего через исходную
точку, до направления на объект.
Магнитный
азимут
Аm
– угол, отсчитываемый по часовой стрелке
от северного направления магнитного
меридиана, проходящего через исходную
точку, до направления на объект.
Угол
между меридианом точки и вертикальными
линиями прямоугольной координатной
сетки называется Гауссовым
сближением меридианов
γ.
Значение можно вычислить по формуле: γ
= (L
– L0)
* sin
B.
Нетрудно заметить, что сближение
меридианов отсутствует на начальных
линиях отсчета: осевом меридиане и
экваторе. Значение Гауссова сближения
меридианов могут быть как положительными,
так и отрицательными, в зависимости от
положения от осевого меридиана. Хотя в
каждой точке может определено уникальное
значение Гауссова сближения меридианов,
их разброс по одному листу карты
незначителен. Поэтому для каждого листа
высчитывают среднее значение сближения
меридианов и указывают его в зарамочном
оформлении.
Угол
между северными направлениями
геодезического и магнитного меридианов
называется магнитным
склонением или
склонением магнитной стрелки D.
Магнитное склонение может быть восточным
(положительным) и западным (отрицательным),
что показывает, с какой стороны от
геодезического проходит магнитный
меридиан.
Величина
магнитного склонения на фиксированную
дату указана в зарамочном оформлении
топографической карты, там же обязательно
присутствует величина ежегодного
изменения магнитного склонения. Для
того, чтобы рассчитать действующее
значение магнитного склонения, необходимо
рассчитать поправку с учетом срока,
прошедшего от фиксированной даты и
прибавить ее к первоначальному значению.
Соотношение
дирекционного угла, геодезического и
магнитного азимутов определяют формулы:
Аг
= α + γ
и Аг
= Аm
+ D.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прямоугольные координаты
(плоские) — линейные величины (абсцисса X и ордината У), определяющие положение точки на плоскости (карте) относительно двух
взаимно перпендикулярных осей X и У. Абсцисса X и ордината У точки А — расстояния от начала
координат до оснований перпендикуляров, опущенных из точки А на соответствующие оси, с указанием знака.
В топографии и геодезии ориентирование производится по северу со счетом углов по ходу часовой стрелки. Поэтому для сохранения знаков тригонометрических
функций положение осей координат, принятое в математике, повернуто на 90° (за ось X принята вертикальная линия, за ось У —
горизонтальная).
Прямоугольные координаты (Гаусса) на топографических картах
применяются по координатным зонам, на которые делится поверхность Земли при изображении ее на картах в проекции Гаусса. Координатные зоны — части земной
поверхности, ограниченные меридианами с долготой, кратной 6°. Счет зон идет от Гринвичского меридиана с запада на восток. Первая зона ограничена
меридианами 0 и 6°, вторая — 6° и 12°, третья —12° и 18° и т.д. (например, территория СССР располагалась в 29 зонах: от 4-й до 32-й включительно).
Протяженность каждой зоны с севера на юг составляет примерно 20 000 км. Ширина зоны на экваторе равна примерно 670 км, на широте 40° — 510 км, на широте
50° — 430 км, на широте 60° — 340 км.
Все топографические карты в пределах одной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения
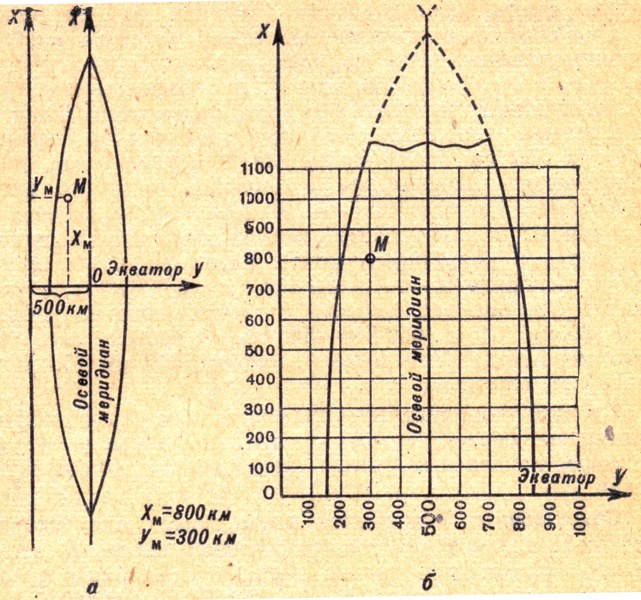
среднего (осевого) меридиана зоны с экватором (рис.2.1), средний меридиан зоны соответствует оси абсцисс (X), а экватор — оси
ординат (Y).
Рис. 2.1 Система прямоугольных координат на топографических картах:
а – одной зоны;
б – части зоны
При таком расположении координатных осей абсциссы точек, расположенных южнее экватора, и ординаты точек, расположенных западнее среднего меридиана, будут
иметь отрицательные значения. Для удобства пользования координатами на топографических картах принят условный счет ординат, исключающий отрицательные
значения координаты У. Это вызвано тем, что отсчет ординат идет не от нуля, а от величины 500 км, т.е. начало координат в каждой зоне как бы
перенесено на 500 км влево вдоль оси У.
Кроме того, для однозначного определения положения точки по прямоугольным координатам на земном шаре к значению координаты у слева приписывается
номер зоны (однозначное или двузначное число). Если, например, точка имеет координаты х = 5 650 450; у = 3 620 840, то это значит, что
она расположена в третьей зоне на удалении 120 км 840 м (620 840 — 500 000) к востоку от среднего меридиана зоны и на удалении 5 650 км 450 м к
северу от экватора.
Полные координаты
— прямоугольные координаты, указанные полностью, без каких-либо сокращений. В примере, приведенном выше, даны полные координаты точки.
Сокращенные координаты
применяются для ускорения целеуказания по топографической карте. В этом случае указывают только десятки и единицы километров и метры, например, х = 50 450; у = 20 840. Сокращенные координаты нельзя применять, если район действий охватывает пространство протяженностью более 100 км
по широте или долготе.
Координатная (километровая) сетка
(рис.2.2) — сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных
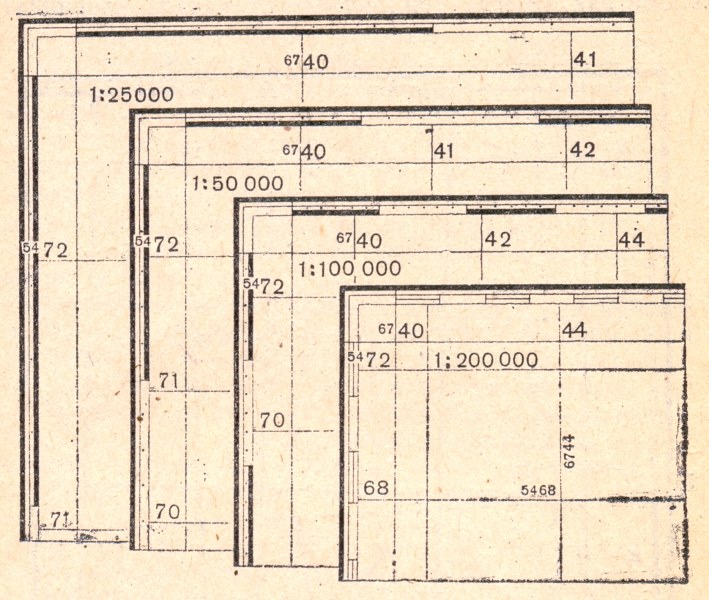
координат через определенные интервалы: на карте масштаба 1:25000 — через 4 см, на картах масштабов 1:50000, 1:100000 и 1:200000 — через 2 см. Эти линии
называются километровыми.
Рис. 2.2 Координатная (километровая) сетка на топографических картах различных масштабов
На карте масштаба 1:500000 координатная сетка полностью не показывается, наносятся только выходы километровых линий по сторонам рамки (через 2 см). При
необходимости по этим выходам координатная сетка может быть прочерчена на карте.
Координатная сетка используется для определения прямоугольных координат и нанесения на карту точек, объектов, целей по их координатам, для целеуказания и
отыскания на карте различных объектов (пунктов), для ориентирования карты на местности, измерения дирекционных углов, приближенного определения расстояний
и площадей.
Километровые линии на картах подписываются у их выходов за рамкой листа и в девяти местах внутри листа карты. Ближайшие к углам рамки километровые линии,
а также ближайшее к северо-западному углу пересечение линий подписываются полностью, остальные сокращенно, двумя цифрами (указываются только десятки и
единицы километров). Подписи у горизонтальных линий соответствуют расстояниям от оси ординат (от экватора) в километрах. Например, подпись 6082 в правом
верхнем углу (рис.2.3) показывает, что данная линия отстоит от экватора на удалении 6 082 км.
Подписи у вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно
перенесенного к западу от среднего меридиана на 500 км. Например, подпись 4308 в левом верхнем углу означает: 4 — номер зоны, 308 — расстояние от условного
начала координат в километрах.
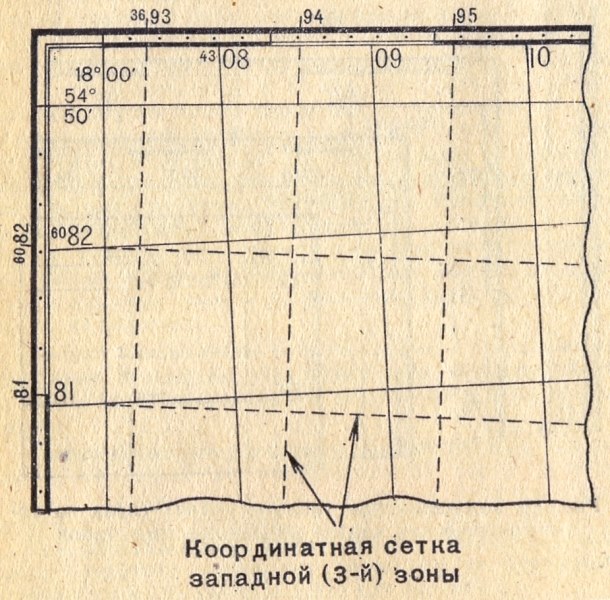
Рис. 2.3 Дополнительная координатная сетка
Дополнительная координатная (километровая) сетка
предназначается для преобразования координат одной зоны в систему координат другой, соседней зоны. Она может быть нанесена на топографических картах
масштабов 1:25000, 1:50000, 1:100000 и 1:200000 по выходам километровых линий в смежной западной или восточной зоне. Выходы километровых линий в виде
черточек с соответствующими подписями даются на картах, расположенных на протяжении 2° к востоку и западу от граничных меридианов зоны.
На рис.2.3 черточки на внешней стороне западной рамки с подписями 81 6082 и на северной стороне рамки с подписями 3693 94 95 обозначают выходы километровых
линий в системе координат смежной (третьей) зоны. При необходимости дополнительная координатная сетка прочерчивается на листе карты путем соединения
одноименных черточек на противоположных сторонах рамки. Вновь построенная сетка является продолжением километровой сетки листа карты смежной зоны и должна
полностью совпадать (смыкаться) с ней при склейке карты.
Определение прямоугольных координат точек по карте
. Вначале измеряют по перпендикуляру расстояние от точки до нижней километровой линии, по масштабу определяют его действительную величину в метрах и
приписывают справа к подписи километровой линии. При длине отрезка более километра вначале суммируют километры, а затем также приписывают число метров
справа. Это будет координата х (абсцисса). Таким же образом определяют и координату у (ординату), только расстояние от точки измеряют до
левой стороны квадрата.
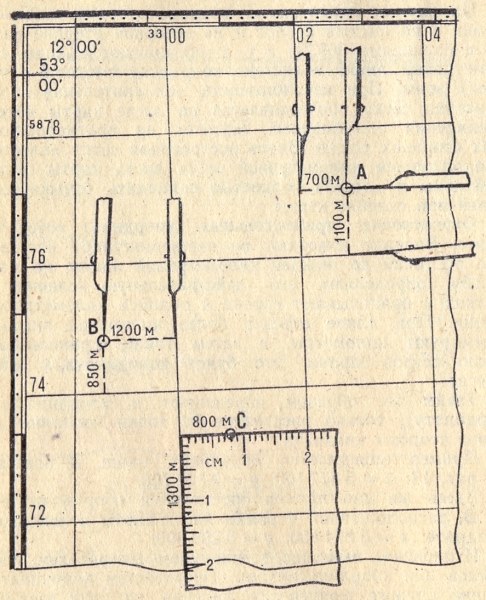
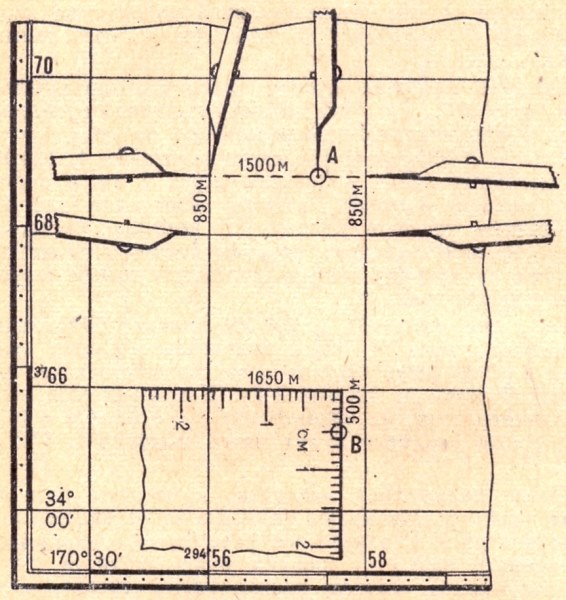
Пример определения координат точки А показан на рис.2.4: х = 5 877 100; у = 3 302 700. Здесь же дан пример определения координат
точки В, расположенной у рамки листа карты в неполном квадрате: х = 5 874 850; у = 3 298 800.
Рис. 2.4 Определение прямоугольных координат точек по карте
Измерения выполняют циркулем-измерителем, линейкой или координатомером. Простейшим координатомером служит офицерская линейка, на двух взаимно
перпендикулярных краях которой имеются миллиметровые деления и надписи х и у.
При определении координат координатомер накладывают на квадрат, в котором располагается точка, и, совместив вертикальную шкалу с его левой стороной, а
горизонтальную — с точкой, как показано на рис.2.4, снимают отсчеты.
Отсчеты в миллиметрах (десятые миллиметра отсчитывают на глаз) в соответствии с масштабом карты преобразуют в действительные величины — километры и
метры, а затем величину, полученную по вертикальной шкале, суммируют (если она больше километра) с оцифровкой нижней стороны квадрата или приписывают к
ней справа (если величина меньше километра). Это будет координата х точки.
Таким же образом получают и координату у — величину, соответствующую отсчету по горизонтальной шкале, только суммирование производят с оцифровкой
левой стороны квадрата.
На рис.2.4 показан пример определения прямоугольных координат точки С: х = 5 873 300; у = 3 300 800.
Нанесение точек на карту по прямоугольным координатам. Прежде всего, по координатам в километрах и оцифровкам километровых линий находят на карте квадрат,
в котором должна быть расположена точка.
Квадрат местонахождения точки на карте масштаба 1:50000, где километровые линии проведены через 1 км, находят непосредственно по координатам объекта в
километрах. На карте масштаба 1:100000 километровые линии проведены через 2 км и подписаны четными числами, поэтому если одна или две координаты точки в.
километрах нечетные числа, то нужно находить квадрат, стороны которого подписаны числами на единицу меньше соответствующей координаты в километрах.
На карте масштаба 1:200000 километровые линии проведены через 4 км и подписаны числами, кратными 4. Они могут быть меньше соответствующей координаты
точки на 1, 2 или 3 км. Например, если даны координаты точки (в километрах) х = 6755 и у = 4613, то стороны квадрата будут иметь оцифровки 6752 и
4612.
После нахождения квадрата, в котором расположена точка, рассчитывают удаление ее от нижней стороны квадрата и полученное расстояние откладывают в
масштабе карты от нижних углов квадрата вверх. К полученным точкам прикладывают линейку и от левой стороны квадрата также в масштабе карты откладывают
расстояние, равное удалению объекта от этой стороны.
На рис.2.5 показан пример нанесения на карту точки А по координатам х = 3 768 850, у = 29 457 500.
Рис. 2.5 Нанесение точек на карту по прямоугольным координатам
При работе с координатомером вначале также находят квадрат, в котором расположена точка. На этот квадрат накладывают координатомер, совмещают его
вертикальную шкалу с западной стороной квадрата так, чтобы против нижней стороны квадрата был отсчет, соответствующий координате х. Затем, не
изменяя положения координатомера, находят на горизонтальной шкале отсчет, соответствующий координате у. Точка против отсчета покажет ее
местоположение, соответствующее данным координатам.
На рис.2.5 показан пример нанесения на карту точки В, расположенной в неполном квадрате, по координатам х = 3 765 500; у = 29 457 650.
В данном случае координатомер наложен так, что горизонтальная шкала его совмещена с северной стороной квадрата, а отсчет против западной его стороны
соответствует разности координаты у точки и оцифровки этой стороны (29 457 км 650 м — 29 456 км = 1 км 650 м). Отсчет, соответствующий разности
оцифровки северной стороны квадрата и координаты х (3766 км — 3765км 500 м), отложен по вертикальной шкале вниз. Местоположение точки В
будет против штриха у отсчета 500 м.
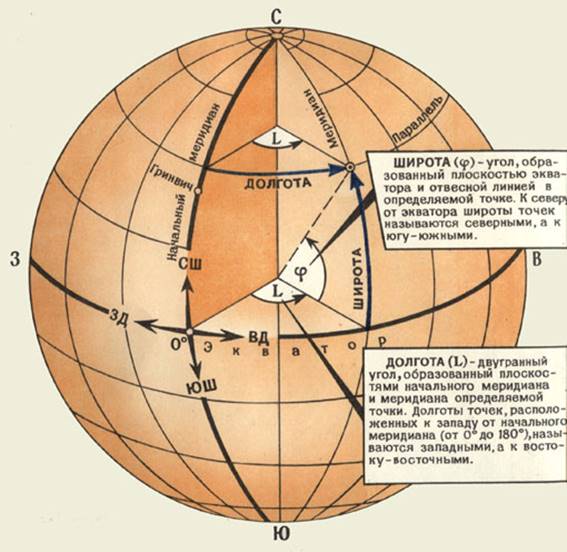
Напомним, что географические координаты (широта и долгота) – это угловые величины, определяющие
положение объектов на земной поверхности и на карте. При этом широта точки — это угол, составленный плоскостью экватора и нормалью к поверхности земного
эллипсоида, проходящей через данную точку. Счет широт ведется по дуге меридиана от экватора к полюсам от 0 до 90°; в северном полушарии широты называют
северными (положительными), в южном — южными (отрицательными).
Долгота точки — это двугранный угол между плоскостью Гринвичского меридиана и плоскостью меридиана данной точки. Счет долготы ведется по дуге экватора
или параллели в обе стороны от начального меридиана, от 0 до 180°. Долготу точек, расположенных к востоку от Гринвича до 180°, называют восточной
(положительной), к западу — западной (отрицательной).
Географическая (картографическая, градусная) сетка
— изображение на карте линий параллелей и меридианов; используется для определения географических (геодезических) координат точек (объектов) и
целеуказания. На топографических картах линии параллелей и меридианов являются внутренними рамками листов; их широта и долгота подписываются на углах
каждого листа. Географическая сетка полностью показывается лишь на топографических картах масштаба 1:500000 (параллели проведены через 30′, а меридианы —
через 20′) и 1:1000000 (параллели проведены через 1°, а меридианы — через 40′). Внутри каждого листа карты на линиях параллелей и меридианов подписаны их
широта и долгота, которые позволяют определять географические координаты на большой склейке карт.
На картах масштабов 1:25000, 1:50000, 1:100000 и 1:200000 стороны рамок разделены на отрезки, равные в градусной мере 1′. Минутные отрезки оттенены через
один и разделены точками (за исключением карты масштаба 1:200000) на части по 10″. Кроме того, внутри каждого листа карт масштабов 1:50000 и 1:100000
показывается пересечение средних параллели и меридиана и дается их оцифровка в градусах и минутах, а вдоль внутренней рамки даны выходы минутных делений
штрихами длиной 2—3 мм, по которым можно прочертить параллели и меридианы на карте, склеенной из нескольких листов.
Если территория, на которую создана карта, находится в западном полушарии, то в северо-западном углу рамки листа правее подписи долготы меридиана
помещается надпись «К западу от Гринвича».
Определение географических координат точки по карте производится по ближайшим к ней параллели и меридиану, широта и долгота которых известны. Для этого на
картах, масштабов 1:25000 — 1:200000 следует предварительно провести южнее точки параллель и западнее — меридиан, соединив линиями соответствующие штрихи
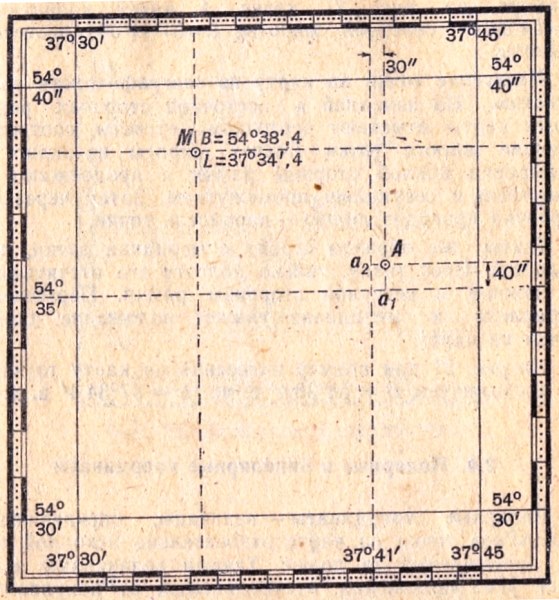
по сторонам рамки листа (рис.2.6). Затем от проведенных линий берут отрезки до определяемой точки (Аа1 Аа2), прикладывают
их к градусным шкалам на сторонах рамки и производят отсчеты. В примере на рис.1.2.6 точка А имеет координаты В = 54°35’40» северной широты, L = 37°41’30» восточной долготы.
Нанесение точки на карту по географическим координатам
. На западной и восточной сторонах рамки листа карты отмечают черточками отсчеты, соответствующие широте точки. Отсчет широты начинают от оцифровки южной
стороны рамки и продолжают по минутным и секундным промежуткам. Затем через эти черточки проводят линию — параллель точки.
Таким же образом строят и меридиан точки, проходящий через точку, только долготу его отсчитывают по южной и северной сторонам рамки. Пересечение параллели
и меридиана укажет положение данной точки на карте. На рис.2.6 дан пример нанесения на карту точки М по координатам В = 54°38,4′ с.ш., L = 37°34,4′ в.д.
Рис. 2.6 Определение географических координат по карте и нанесение точек на карту по географическим координатам
Как было указано выше, в силу особенностей формы, внутреннего строения и движения в пространстве земной эллипсоид имеет истинные (географические) и
магнитные полюса, не совпадающие друг с другом.
Северный и Южный географические полюсы — это точки, через которые проходит ось вращения земного шара, а Северный и Южный магнитные полюсы – это полюсы
гигантского магнита, которым, собственно, является Земля, причем Северный магнитный полюс (≈ 74°с.ш., 100°з.д.) и Южный магнитный полюс (≈ 69°ю.ш.,
144°в.д.) постепенно дрейфуют и, соответственно, не имеют постоянных координат. В этой связи важно понимать, что магнитная стрелка компаса указывает именно
на магнитный, а не на истинный (географический) полюс.
Таким образом, существуют истинный и магнитный полюсы, не совпадающие между собой, соответственно этому существуют истинный (географический) и магнитный меридианы. И от того и от другого можно отсчитывать направление
на нужный объект: в одном случае наблюдатель будет иметь дело с истинным азимутом, в другом — с магнитным.
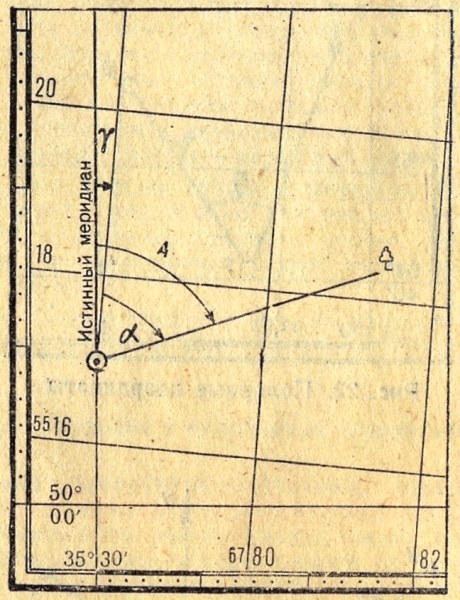
Рис. 2.7 Истинный азимут А, дирекционный угол α, и сближение меридианов γ
Истинный азимут
— это угол А (рис.2.7), измеряемый по ходу часовой стрелки от 0 до 360° между северным направлением истинного (географического)
меридиана и направлением на определяемый пункт.
Магнитный азимут
— это угол Ам, измеряемый по ходу часовой стрелки от 0 до 360° между заданным (выбранным) направлением и направлением
на Север на местности.
Обратный азимут
— азимут (истинный, магнитный) направления, противоположного определяемому (прямому). Он отличается от прямого на 180°, и его можно отсчитать по компасу
против указателя у прорези.
Понятно, что истинный и магнитный азимуты отличаются, как минимум, на ту же самую величину, на которую магнитный меридиан отличается от истинного. Эта
величина называется магнитным склонением. Другими словами, магнитное склонение – угол δ ( дельта) между истинным и магнитным меридианами.
На величину магнитного склонения оказывают влияние различные магнитные аномалии (залежи руд, подземные потоки и т.д.), суточные, годовые и вековые
колебания, а также временные возмущения под действием магнитных бурь. Величина магнитного склонения и его годовые изменения указаны на каждом листе
топографической карты. Суточное колебание магнитного склонения достигает 0,3° и при точных измерениях магнитного азимута учитывается по графику поправок,
составленному в зависимости от времени суток. На картах масштабов 1:500000 и 1:1000000 показываются районы магнитных аномалий, и в каждом из них
подписывается значение амплитуды колебания магнитного склонения. Если стрелка компаса отклоняется от истинного меридиана к востоку, магнитное склонение
называют восточным (положительным), если стрелка отклоняется к западу, склонение называют западным (отрицательным). Соответственно, восточное склонение
часто обозначают знаком «+», западное — знаком «—».
Дирекционный угол
— это угол α (альфа), измеряемый на карте по ходу часовой стрелки от 0 до 360° между северным направлением вертикальной
линии координатной сетки и направлением на определяемый пункт. Другими словами, дирекционный угол — это угол между заданным (выбранным) направлением и
направлением на Север на карте (рис.2.7). Дирекционные углы измеряются по карте, а также определяются по измеренным на местности
магнитным или истинным азимутам.
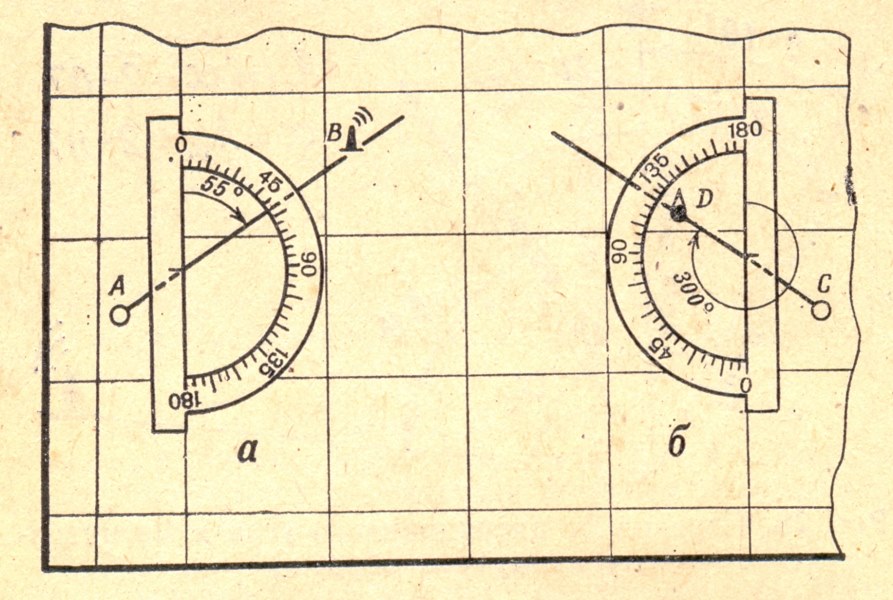
Рис. 2.8 Измерение дирекционного угла транспортиром
Измерение и построение дирекционных углов на карте производится с помощью транспортира (рис.2.8).
Чтобы измерить на карте дирекционный угол какого-нибудь направления, надо наложить на нее транспортир так, чтобы середина его линейки, отмеченная
штрихом, совпала с точкой пересечения определяемого направления с вертикальной километровой линией сетки, а край линейки (т.е. деления 0 и 180° на
транспортире) совместился с этой линией. Затем следует отсчитать по шкале транспортира угол по ходу часовой стрелки от северного направления километровой
линии до определяемого направления.
Для построения на карте в какой-либо точке дирекционного угла проводят через эту точку прямую, параллельную вертикальным линиям километровой сетки,
и от этой прямой строят заданный дирекционный угол.
Следует учитывать, что средняя ошибка измерения угла транспортиром, имеющимся на офицерской линейке, составляет 0,5°.
Значения истинного азимута и дирекционного угла отличаются друг от друга на величину сближения меридианов. Сближение меридианов —
угол ? (гамма) между северным направлением истинного меридиана данной точки и вертикальной линией координатной сетки
(рис.2.7). Сближение меридианов отсчитывается от северного направления истинного меридиана до северного направления вертикальной линии сетки. Для точек,
расположенных восточнее среднего меридиана зоны, величина сближения положительная, а для точек, расположенных западнее, — отрицательная. Величина
сближения меридианов на осевом меридиане зоны равна нулю и возрастает с удалением от среднего меридиана зоны и от экватора, при этом ее максимальное
значение не превышает 3°.
Сближение меридианов, указываемое на топографических картах, относится к средней (центральной) точке листа; величина ее в пределах листа карты масштаба
1:100000 на средних широтах у западной или восточной рамки может отличаться на 10-15′ от значения, подписанного на карте.
Переход от дирекционного угла к магнитному азимуту и обратно
может производиться различными способами: по формуле, с учетом годового изменения магнитного склонения, по графической схеме. Удобен переход через поправку
направления. Необходимые данные для этого имеются на каждом листе карты масштабов 1:25000—1:200000 в специальной текстовой справке и графической схеме,
помещаемых на полях листа в левом нижнем углу (рис.2.9).
Рис. 2.9 Данные о величине поправки направления
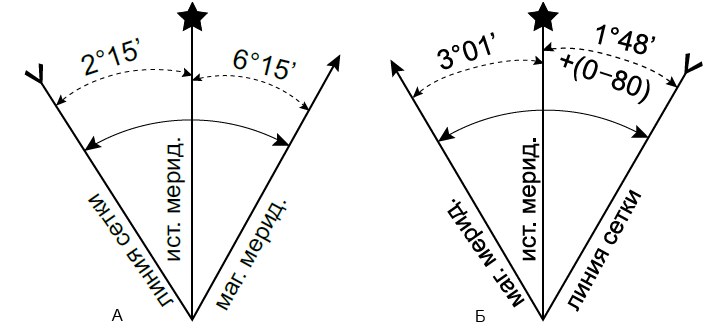
При этом в специальной текстовой справке ключевой фразой является: «Поправка в дирекционный угол при переходе к магнитному азимуту плюс (минус)…»,
также важен угол между «стрелочкой» и «вилочкой»:
-
если «вилочка» слева, а «стрелочка» справа (рис.2.10-А), то склонение восточное и при переходе от дирекционного угла к азимуту
поправка (2°15′ + 6°15′ = 8°30′) от величины измеренного дирекционного угла отнимается (соответственно, при
переходе от азимута к дирекционному углу, поправка прибавляется); -
если «вилочка» справа, а «стрелочка» слева (рис.2.10-Б), то склонение западное и при переходе от дирекционного угла к азимуту
поправка (3°01′ + 1°48′ = 4°49′) к величине измеренного дирекционного угла прибавляется (соответственно, при
переходе от азимута к дирекционному углу, поправка отнимается).
Рис. 2.10 Внесение поправки
Внимание!
Невнесение поправки в дирекционный угол или магнитный азимут, особенно при больших расстояниях и крупных масштабах карт, ведет к значительным ошибкам в
определении координат, промежуточных и конечных точек маршрута.
Содержание конспекта
- 1. Системы координат, применяемые в топографии: географические, плоские прямоугольные, полярные и биполярные координаты, их сущность и использование
- 2. Определение географических координат и нанесение на карту объектов по известным координатам
- 3. Прямоугольная координатная сетка на топографических картах и ее оцифровка. Дополнительная сетка на стыке координатных зон
- 4. Определение прямоугольных координат точек. Нанесение на карту точек по их координатам
- 5. Точность определения координат на картах различных масштабов
- 6. Определение положения объектов (точек) в системах полярных и биполярных координат, нанесение на карту объектов по направлению и расстоянию, по двум углам или по двум расстояниям
- 7. Способы целеуказания по карте: в графических координатах, плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, от условной линии, по азимуту и дальности цели, в системе биполярных координат
- 8. Решение задач
1. Системы координат, применяемые в топографии: географические, плоские прямоугольные, полярные и биполярные координаты, их сущность и использование
Координатами называются угловые и линейные величины (числа), определяющие положение точки на какой-либо поверхности или в пространстве.
В топографии применяют, такие системы координат, которые позволяют наиболее просто и однозначно определять положение точек земной поверхности как по результатам непосредственных измерений на местности, так и с помощью карт. К числу таких систем относятся географические, плоские прямоугольные, полярные и биполярные координаты.
Географические координаты (рис.1) – угловые величины: широта (j) и долгота (L), определяющие положение объекта на земной поверхности относительно начала координат – точки пересечения начального (Гринвичского) меридиана с экватором. На карте географическая сетка обозначена шкалой на всех сторонах рамки карты. Западная и восточная стороны рамки являются меридианами, а северная и южная – параллелями. В углах листа карты подписаны географические координаты точек пересечения сторон рамки.
В системе географических координат положение любой точки земной поверхности относительно начала координат определяется в угловой мере. За начало у нас и в большинстве других государств принята точка пересечения начального (Гринвичского) меридиана с экватором. Являясь, таким образом, единой для всей нашей планеты, система географических координат удобна для решения задач по определению взаимного положения объектов, расположенных на значительных расстояниях друг от друга. Поэтому в военном деле эту систему используют главным образом для ведения расчетов, связанных с применением боевых средств дальнего действия, например баллистических ракет, авиации и др.
Плоские прямоугольные координаты (рис. 2) – линейные величины, определяющие положение объекта на плоскости относительно принятого начала координат – пересечение двух взаимно перпендикулярных прямых (координатных осей Х и Y).
В топографии каждая 6-градусная зона имеет свою систему прямоугольных координат. Ось Х — осевой меридиан зоны, ось Y – экватор, а точка пересечения осевого меридиана с экватором – начало координат.
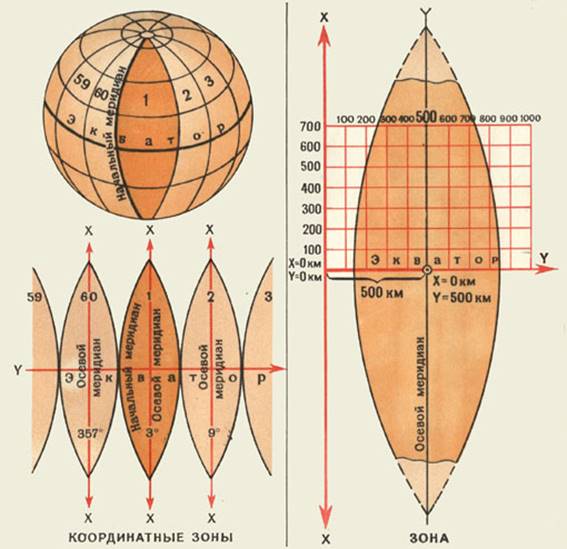
Система плоских прямоугольных координат является зональной; она установлена для каждой шестиградусной зоны, на которые делится поверхность Земли при изображении ее ни картах в проекции Гаусса, и предназначена для указания положения изображений точек земной поверхности на плоскости (карте) в этой проекции.
Началом координат в зоне является точка пересечения осевого меридиана с экватором, относительно которой и определяется в линейной мере положение всех остальных точек зоны. Начало координат зоны и ее координатные оси занимают строго определенное положение на земной поверхности. Поэтому система плоских прямоугольных координат каждой зоны связана как с системами координат всех остальных зон, так и с системой географических координат.
Применение линейных величин для определения положения точек делает систему плоских прямоугольных координат весьма удобной для ведения расчетов как при работе на местности, так и на карте. Поэтому в войсках эта система находит наиболее широкое применение. Прямоугольными координатами указывают положение точек местности, своих боевых порядков и целей, с их помощью определяют взаимное положение объектов в пределах одной координатной зоны или на смежных участках двух зон.
Системы полярных и биполярных координат являются местными системами. В войсковой практике они применяются для определения положения одних точек относительно других на сравнительно небольших участках местности, например при целеуказании, засечке ориентиров и целей, составлении схем местности и др. Эти системы могут быть связаны с системами прямоугольных и географических координат.
2. Определение географических координат и нанесение на карту объектов по известным координатам
Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна.
Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом. На боковых сторонах рамки обозначены широты, а на северной и южной — долготы.
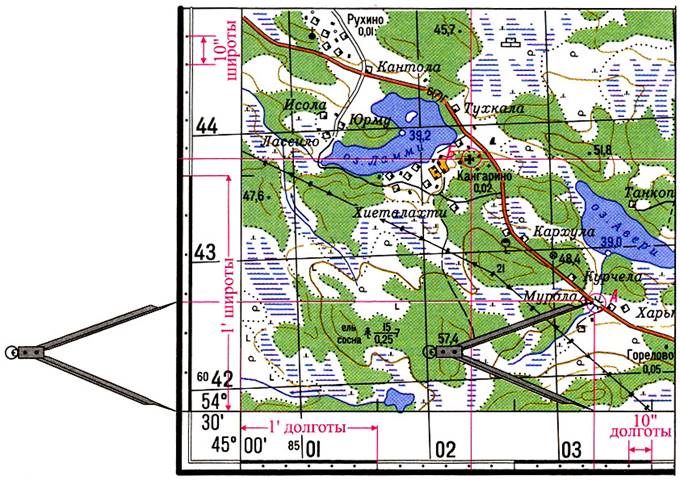
Пользуясь минутной рамкой карты можно:
1. Определить географические координаты любой точки на карте.
Например, координаты точки А (рис.3). Для этого необходимо с помощью циркуля-измерителя измерить кратчайшее расстояние от точки А до южной рамки карты, затем приложить измеритель к западной рамке и определить количество минут и секунд в измеренном отрезке, сложить полученное (измеренное) значение минут и секунд (0’27») с широтой юго-западного угла рамки — 54°30′.
Широта точки на карте будет равна: 54°30’+0’27» = 54°30’27».
Долгота определяется аналогично.
Измеряют с помощью циркуля-измерителя кратчайшее расстояние от точки А до западной рамки карты, прикладывают циркуль-измеритель к южной рамке, определяют количество минут и секунд в измеренном отрезке (2’35») складывают полученное (измеренное) значение с долготой юго-западного угла рамки — 45°00′.
Долгота точки на карте будет равна: 45°00’+2’35» = 45°02’35»
2. Нанести любую точку на карту по заданным географическим координатам.
Например, точку Б широта: 54°31 ’08», долгота 45°01 ’41».
Для нанесения на карту точки по долготе необходимо провести истинный меридиан через данную точку, для чего соединить одинаковое количество минут по северной и южной рамке; для нанесения на карту точки по широте необходимо провести параллель через данную точку, для чего соединить одинаковое количество минут по западной и восточной рамке. Пересечение двух прямых определит местоположение точки Б.
3. Прямоугольная координатная сетка на топографических картах и ее оцифровка. Дополнительная сетка на стыке координатных зон
Координатная сетка на карте представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проведены через целое число километров. Поэтому координатную сетку называют также километровой сеткой, а ее линии километровыми.
На карте 1:25000 линии, образующие координатную сетку, проведены через 4 см, то есть через 1 км на местности, а на картах 1:50000-1:200000 через 2 см (1,2 и 4 км на местности соответственно). На карте 1:500000 наносятся лишь выходы линий координатной сетки на внутренней рамке каждого листа через 2 см (10 км на местности). При необходимости по этим выходам координатные линии могут быть нанесены на карту.
На топографических картах значения абсцисс и ординат координатных линий (рис. 2) подписывают у выходов линий за внутренней рамкой листа и девяти местах на каждом листе карты. Полные значения абсцисс и ординат в километрах подписываются около ближайших к углам рамки карты координатных линий и около ближайшего к северо-западному углу пересечения координатных линий. Остальные координатные линии подписываются сокращенно двумя цифрами (десятки и единицы километров). Подписи около горизонтальных линий координатной сетки соответствуют расстояниям от оси ординат в километрах.
Подписи около вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от осевого меридиана зоны на 500 км. Например, подпись 6740 означает: 6 — номер зоны, 740 — расстояние от условного начала координат в километрах.
На внешней рамке даны выходы координатных линий (дополнительная сетка) системы координат смежной зоны.
4. Определение прямоугольных координат точек. Нанесение на карту точек по их координатам
По координатной сетке с помощью циркуля (линейки) можно:
1. Определить прямоугольные координаты точки на карте.
Например, точки В (рис. 2).
Для этого надо:
- записать X — оцифровку нижней километровой линии квадрата, в котором находится точка В, т. е. 6657 км;
- измерить по перпендикуляру расстояние от нижней километровой линии квадрата до точки В и, пользуясь линейным масштабом карты, определить величину этого отрезка в метрах;
- сложить измеренную величину 575 м с значением оцифровки нижней километровой линии квадрата: X=6657000+575=6657575 м.
Определение ординаты Y производят аналогично:
- записать значение Y — оцифровку левой вертикальной линии квадрата, т.е.7363;
- измерить по перпендикуляру расстояние от этой линии до точки В, т. е.335 м;
- прибавить измеренное расстояние к значению оцифровки Y левой вертикальной линии квадрата: Y=7363000+335=7363335 м.
2. Нанести на карту цель по заданным координатам.
Например, точку Г по координатам: Х=6658725 Y=7362360.
Для этого надо:
- найти квадрат, в котором расположена точка Г по значению целых километров, т. е. 5862;
- отложить от левого нижнего угла квадрата отрезок в масштабе карты, равный разности абсциссы цели и нижней стороны квадрата — 725 м;
- от полученной точки по перпендикуляру вправо отложить отрезок, равный разности ординат цели и левой стороны квадрата, т. е. 360 м.
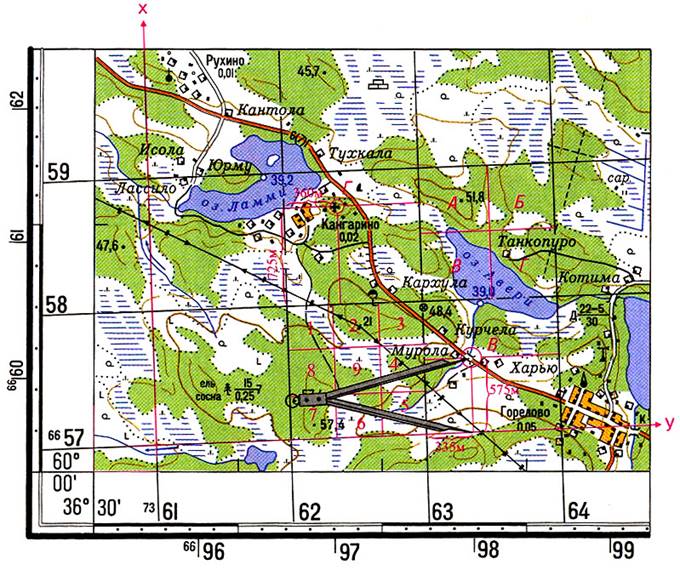
5. Точность определения координат на картах различных масштабов
Точность определения географических координат по картам 1:25000-1:200000 составляет около 2 и 10» соответственно.
Точность определения по карте прямоугольных координат точек ограничивается не только ее масштабом, но и величиной погрешностей, допускаемых при съемке или составлении карты и нанесении на нее различных точек и объектов местности
Наиболее точно (с ошибкой, не превышающей 0,2 мм) на карту наносятся геодезические пункты и. наиболее резко выделяющиеся на местности и видимые издали предметы, имеющие значение ориентиров (отдельные колокольни, фабричные трубы, постройки башенного типа). Поэтому координаты таких точек можно определить примерно с той же точностью, с которой они на карту наносятся, т. е. для карты масштаба 1:25000 — с точностью — 5-7 м, для карты масштаба 1:50000 — с точностью — 10-15 м, для карты масштаба 1:100000 — с точностью — 20-30 м.
Остальные ориентиры и точки контуров наносятся на карту, а, следовательно, и определяются по ней с ошибкой до 0,5 мм, а точки, относящиеся к нечетко выраженным на местности контурам (например, контур болота), с ошибкой до 1 мм.
6. Определение положения объектов (точек) в системах полярных и биполярных координат, нанесение на карту объектов по направлению и расстоянию, по двум углам или по двум расстояниям
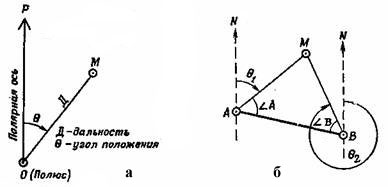
Система плоских полярных координат (рис. 3, а) состоит из точки О — начало координат, или полюса, и начального направления ОР, называемого полярной осью.
Положение точки М на местности или на карте в этой системе определяется двумя координатами: углом положения θ, который измеряется по ходу часовой стрелки от полярной оси до направления на определяемую точку М (от 0 до 360°), и расстоянием ОМ=Д.
В зависимости от решаемой задачи за полюс принимают наблюдательный пункт, огневую позицию, исходный пункт движения и т. п., а за полярную ось — географический (истинный) меридиан, магнитный меридиан (направление магнитной стрелки компаса) или же направление на какой-либо ориентир.
Этими координатами могут служить либо два угла положения, определяющих направления с точек А и В на искомую точку М, либо расстояния D1=АМ и D2=ВМ до нее. Углы положения при этом, как показано на рис. 1, б, измеряются в точках А и В или от направления базиса (т. е. угол А=ВАМ и угол В=АВМ) или от других каких-либо направлений, проходящих через точки А и В и принимаемых за начальные. Например, во втором случае место точки М определено углами положения θ1 и θ2, измеренными от направления магнитных меридианов.Система плоских биполярных (двухполюсных) координат (рис. 3, б) состоит из двух полюсов А и В и общей оси АВ, называемой базисом или базой засечки. Положение любой точки М относительно двух данных на карте (местности) точек А и В определяется координатами, которые измеряются на карте или на местности.
Нанесение обнаруженного объекта на карту
Это один из важнейших моментов в обнаружении объекта. От того, насколько точно объект (цель) будет нанесен на карту, зависит точность определения его координат.
Обнаружив объект (цель), необходимо сначала точно определить по различным признакам, что обнаружено. Затем, не прекращая наблюдение за объектом и не обнаруживая себя, нанести объект на карту. Для нанесения объекта на карту существуют несколько способов.
Глазомерно: объект наносится на карту, если он находится вблизи известного ориентира.
По направлению и расстоянию: для этого необходимо сориентировать карту, найти на ней точку своего стояния, свизировать на карте направление на обнаруженный объект и прочертить линию до объекта от точки своего стояния, затем определить расстояние до объекта, измерив это расстояние на карте и соизмерив его с масштабом карты.
Если таким образом графически невозможно решить задачу (мешает противник, плохая видимость и др.), то нужно точно измерить азимут на объект, затем перевести его в дирекционный угол и прочертить на карте из точки стояния направление, на котором отложить расстояние до объекта.
Чтобы получить дирекционный угол, надо к магнитному азимуту прибавить магнитное склонение данной карты (поправка направления).
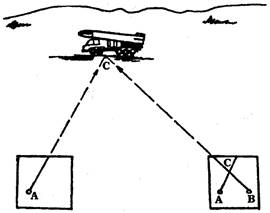
Прямой засечкой. Этим способом наносят объект на карту из 2-х-3-х точек, с которых можно вести наблюдение за ним. Для этого из каждой выбранной точки прочерчивается на ориентированной карте направление на объект, тогда пересечение прямых линий определяет местонахождение объекта.
7. Способы целеуказания по карте: в графических координатах, плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, от условной линии, по азимуту и дальности цели, в системе биполярных координат
Умение быстро и правильно указывать цели, ориентиры и другие объекты на местности имеет важное значение для управления подразделениями и огнем в бою или для организации боя.
Целеуказания в географических координатах применяется очень редко и только в тех случаях, когда цели удалены от заданной точки на карте на значительном расстоянии, выражающемся в десятках или сотнях километров. При этом географические координаты определяются по карте, как описано в вопросе № 2 настоящего занятия.
Местоположение цели (объекта) указывают широтой и долготой, например, высота 245,2 (40° 8′ 40″ с. ш., 65° 31′ 00″ в. д.). На восточную (западную), северную (южную) стороны топографической рамки наносят уколом циркуля отметки положения цели по широте и долготе. От этих отметок в глубину листа топографической карты опускают перпендикуляры до их пересечения (прикладывают командирские линейки, стандартные листы бумаги). Точка пересечения перпендикуляров и есть положение цели на карте.
Для приближенного целеуказания по прямоугольным координатам достаточно указать на карте квадрат сетки, в котором расположен объект. Квадрат всегда указывается цифрами километровых линий, пересечением которых образован юго-западный (нижний левый) угол. При указании квадрата карты придерживаются правила: сначала называют две цифры, подписанные у горизонтальной линии (у западной стороны), то есть координату «X», а затем две цифры у вертикальной линии (южная сторона листа), то есть координата «Y». При этом «X» и «Y» не говорятся. Например, засечены танки противника. При передаче донесения по радиотелефону номер квадрата произносят: «восемьдесят восемь ноль два».
Если положение точки (объекта) необходимо определить более точно, то пользуются полными или сокращенными координатами.
Работа с полными координатами. Например, требуется определить координаты указателя дорог в квадрате 8803 на карте масштаба 1:50000. Сначала определяют чему равно расстояние от нижней горизонтальной стороны квадрата до указателя дорог (например, 600 м на местности). Таким же образом измеряют расстояние от левой вертикальной стороны квадрата (например, 500 м). Теперь путем оцифровки километровых линий определяем полные координаты объекта. Горизонтальная линия имеет подпись 5988 (X), прибавив расстояние от этой линии до указателя дорог, получим: Х=5988600. Точно также определяем вертикальную линию и получаем 2403500. Полные координаты указателя дорог следующие: Х=5988600 м, У=2403500 м.
Сокращенные координаты соответственно будут равны: Х=88600 м, У=03500 м.
Если требуется уточнить положение цели в квадрате, то применяют целеуказание буквенным или цифровым способом внутри квадрата километровой сетки.
При целеуказании буквенным способом внутри квадрата километровой сетки квадрат условно разбивается на 4 части, каждой части присваивается заглавная буква русского алфавита.
Второй способ — цифровой способ целеуказания внутри квадрата километровой сетки (целеуказание по улитке). Этот способ получил свое название по расположению условных цифровых квадратов внутри квадрата километровой сетки. Они расположены как бы по спирали, при этом квадрат разбивается на 9 частей.
При целеуказании в этих случаях называют квадрат, в котором находится цель, и добавляют букву или цифру, уточняющую положение цели внутри квадрата. Например, высота 51,8 (5863-А) или высоковольтная опора (5762-2) (см. рис. 2).
Целеуказание от ориентира наиболее простой и распространенный способ целеуказания. При этом способе целеуказания вначале называют ближайший к цели ориентир, затем величину угла между направлением на ориентир и направлением на цель в делениях угломера (измеряется биноклем) и удаление до цели в метрах. Например: «Ориентир второй, вправо сорок, дальше двести, у отдельного куста – пулемет».
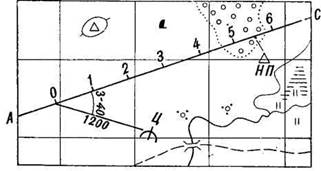
Целеуказание от условной линии обычно применяется в движении на боевых машинах. При этом способе по карте выбирают в направлении действий две точки и соединяют их прямой линией, относительно которой и будет вестись целеуказание. Эту линию обозначают буквами, разбивают на сантиметровые деления и нумеруют их начиная с нуля. Такое построение делается на картах как передающего, так и принимающего целеуказание.
Целеуказание от условной линии обычно применяется в движении на боевых машинах. При этом способе по карте выбирают в направлении действий две точки и соединяют их прямой линией (рис. 5), относительно которой и будет вестись целеуказание. Эту линию обозначают буквами, разбивают на сантиметровые деления и нумеруют их начиная с нуля.
Такое построение делается на картах как передающего, так и принимающего целеуказание.
Положение цели относительно условной линии определяется двумя координатами: отрезком от начальной точки до основания перпендикуляра, опущенного из точки расположения цели на условную линию, и отрезком перпендикуляра от условной линии до цели.
При целеуказании называют условной наименование линии, затем число сантиметров и миллиметров, заключающихся в первом отрезке, и, наконец, направление (влево или вправо) и длину второго отрезка. Например: «Прямая АС, пять, семь; вправо ноль, шесть – НП».
Целеуказание от условной линии можно выдать, указав направление на цель под углом от условной линии и расстояние до цели, например: «Прямая АС, вправо 3-40, тысяча двести – пулемет».
Целеуказание по азимуту и дальности до цели. Азимут направления на цель определяют с помощью компаса в градусах, а дальность до нее – с помощью прибора наблюдения или глазомерно в метрах. Например: «Азимут тридцать пять, дальность шестьсот – танк в окопе». Этот способ чаще всего используют на местности, где мало ориентиров.
8. Решение задач
Определение координат точек местности (объектов) и целеуказание по карте отрабатывается практически на учебных картах по заранее подготовленным точкам (нанесенным объектам).
Каждый обучаемый определение географические и прямоугольные координаты (наносит на карту объекты по известным координатам).
Способы целеуказания по карте отрабатываются: в плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, по азимуту и дальности цели.
Скачать конспект
Линии параллелей и меридианов, которые служат рамкой для данного листа бумажнойтопографической карты, представляют собой кривые линии, хотя кривизна их в пределах одного листа практически и незаметна. Но в пределах каждой зоны Гаусса имеются две линии, которые изображаются на карте прямыми линиями. Это осевой меридиан зоны и экватор. Эти две линии приняты за оси плоских прямоугольных координат и определяют сами плоские прямоугольные координаты.
Плоские прямоугольные координаты, как определить плоские прямоугольные координаты по топографической карте.
Линию осевого меридиана считают осью абсцисс и обозначают х, линию экватора — осью ординат и обозначают у. За начало координат принимают точку пересечения осевого меридиана с экватором. Таким ебразом, в каждой зонеГаусса имеется своя сетка плоских прямоугольных координат. Координаты х (абсциссы) отсчитываются к северу и югу от экватора, то есть от 0 (на экваторе) до 10 000 км (на полюсе).
К северу от экватора координата у считается положительной, к югу — отрицательной. Координаты ху (ординаты) отсчитываются от осевого меридиана вправо (к востоку) и влево (к западу). Чтобы не иметь дела с отрицательными значениями для этих координат, условились значение ординаты у для осевого меридиана принимать равным 500 км.
Тем самым ось х как бы переносится к западу на 500 км и все значения ординат в пределах данной зоны будут иметь всегда положительный знак. Кроме того, к значению ординаты у спереди всегда приписывается цифра, соответствующая номеру зоны Гаусса для того, чтобы избежать повторения координат, расположенных в разных зонах.
Как определить плоские прямоугольные координаты по топографической карте.
Чтобы можно было определить плоские прямоугольные координаты точек в каждой зоне Гаусса на топографическихкартах наносится прямоугольная сетка координат, то есть проводятся линии, параллельные осевому меридиану и экватору.
Эти прямые линии, естественно, не будут совпадать с линиями, изображающими меридианы и параллели. За исключением осевого меридиана и экватора, параллельно которым они проводятся. Эту сетку координат называют километровой, так как ее линии проводятся через километр длямасштабов 1:10 000, 1:25 000, 1:50 000.
На каждом листе карты вдоль внутренней рамки даются значения координат километровой сетки от осевого меридиана данной зоны и от экватора. Значения полных координат подписываются только у крайних (верхней и нижней) линии сетки координат. У всех же промежуточных линий подписываются сокращенные обозначения, то есть только последние две цифры (десятки и единицы километров).
Например, нижняя линия километровой сетки на рисунке имеет обозначение 5042, а следующая над ней линия сетки обозначена только цифрой 43 км, а не 5043. Цифры километровой сетки под южной и над северной рамкой листа карты обозначают ординаты (у) этих линий. Крайние линии также обозначены полными координатами. Но в отличие от горизонтальных линий, первая цифра у ординат обозначает номер зоны.
Например, ордината у = 8384 км. Это значит, что лист данной карты расположен в восьмой шестиградусной зоне Гаусса, то есть ограниченной 42 и 48 меридианами восточной долготы, а точки, лежащие на линии у = 384, расположены слева от осевого меридиана на расстоянии 500-384=116 км.
С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любойточки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат. Сначала обычно называется (записывается) значение координаты х — 5044, а затем у = 8384.
Указание какого-либо объекта на топографической карте с помощью плоских прямоугольных координат.
Для указания какого-либообъекта на карте обычно говорят так: точка М находится в квадрате 50 448 384, то есть называют координаты ее подряд, не разделяя их, но чаще дают указания сокращенно, называют только две последующие цифры из плоских прямоугольных координат данной точки — квадрат 4484.
Называя этот квадрат на карте, мы указываем координаты левого нижнего его угла. То есть юго-западного угла квадрата, в котором расположена точка М. Если необходимо указать более точное положение точки внутри этого квадрата, то дополнительно определяют ее расстояние от граничных линий этого квадрата. Используя масштаб, переводят эти расстояния в метры и приписывают их к цифрам обозначенного квадрата.
Например, точка М имеет следующие координаты: х = 44 500 метров, а у = 84 500 метров. Это и будут сокращенные координаты для точки М, а полные плоские прямоугольные координаты для нее запишутся так: х = 5 044 500 м, у — 384 500 м.
Нанесение точек на карту по известным плоским прямоугольным координатам производится в обратной последовательности. Сначала отбрасываются три последние цифры в координатах и находятся линии километровой сетки. То есть квадрат, в котором расположена точка. Затем, с помощьюлинейки, масштаба и циркуля, наносятся точные координаты данной точки в этом квадрате.
Две сетки плоских прямоугольных координат на топографических картах.
На некоторых топографических картах можно встретить две сетки плоских прямоугольных координат. Одна нанесена полностью так, как это было показано на рисунке выше. Вторая обозначена только за рамкой данной карты. В чем тут дело? Мы уже ранее установили, что вертикальные километровые линии параллельны осевому меридиану своей зоны, а осевые меридианы соседних зон между собой не параллельны.
Следовательно, при стыковке километровых сеток двух соседних зон линии одной из них располагаются под углом к линиям другой. Вследствие этого на стыке двух зон могут возникнуть затруднения вопределении координат, так как они будут относиться к разным осям координат.
Чтобы устранить это неудобство, в каждой шестиградусной зоне все листы карт, расположенные в пределах 2 градусов к востоку и 2 градусов к западу от границы зоны имеют помимо своей координатной сетки еще и дополнительную, являющуюся продолжением координатной сетки соседней зоны.
И для того чтобы не затемнять второй сеткой данные листы карты, ее обозначают лишь цифрами на внешней рамке листа. Цифры эти являются продолжением нумерации линий координатной сетки смежной зоны.
По материалам книги «Карта и компас мои друзья».
Клименко А.И.
Краткая теоретическая информация
В начало справки ⇡
Эллипсоид – математическая фигура,описывающая фигуру Земли и характеризующаяся параметрами малой и большой полуоси.
Географическая (геодезическая) система координат – система координат на эллипсоиде, задающая счёт широтам и долготам в градусах, а также положение эллипсоида внутри тела земли.
Спроецированная (прямоугольная) система координат – система координат проекции, определяющая ориентировку декартовых осей координат и их начало.
Цель работы
В начало справки ⇡
Научиться измерять по топографической карте геодезические и прямоугольные координаты точек, решать обратную геодезическую задачу, определять расстояния и ориентирующие углы.
Выполнение работы в онлайн-вьюере
В начало справки ⇡
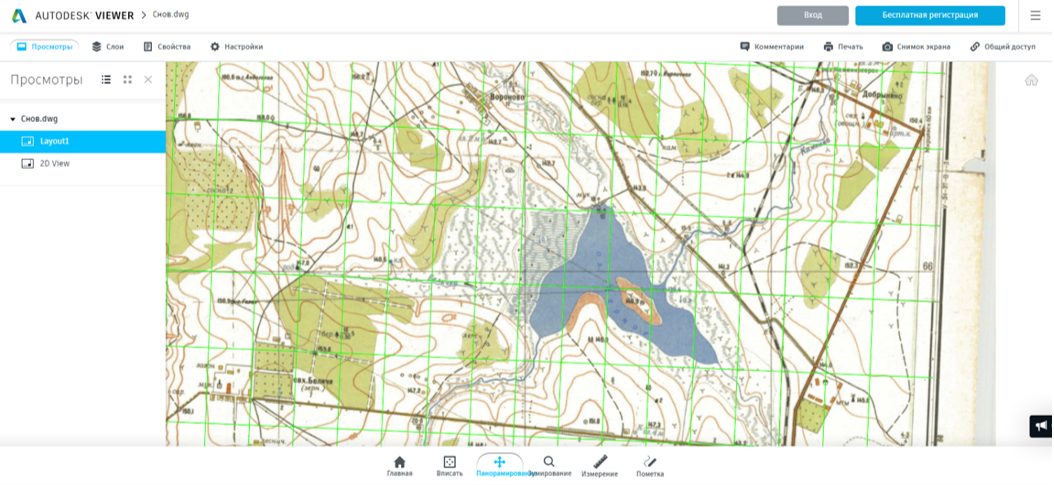
- Запустить онлайн-вьюер. Откроется учебная топографическая карта.
Менять масштаб просматриваемого изображения можно колесиком мыши. Дополнительно в файле точки, соответствующие 10-секундным отрезкам, соединены зелеными линиями. Т.е. это дополнительно проведенные параллели и меридианы.
- Найти две точки на листе топографической карты, к которым будут привязаны все измерения. Указать их названия в шапке бланка.
library(flextable)
library(magrittr)
df <- data.frame(x = 1:10, y = 11:20)
df %>% regulartable() %>% autofit() %>%
width(j=~x,width=1) %>% width(j=~y,width=1)|
x |
y |
|---|---|
|
1 |
11 |
|
2 |
12 |
|
3 |
13 |
|
4 |
14 |
|
5 |
15 |
|
6 |
16 |
|
7 |
17 |
|
8 |
18 |
|
9 |
19 |
|
10 |
20 |
| Точка | |
|---|---|
1-я (A) |
|
2-я (B) |
- Описать лист топографической карты, заполнив таблицу 1 бланка. Указать масштаб карты (численный вид), номер зоны, долготу осевого меридиана зоны, номенклатуру.
| Номенклатура | |
| Номер зоны | |
| Долгота осевого | |
| Масштаб карты |
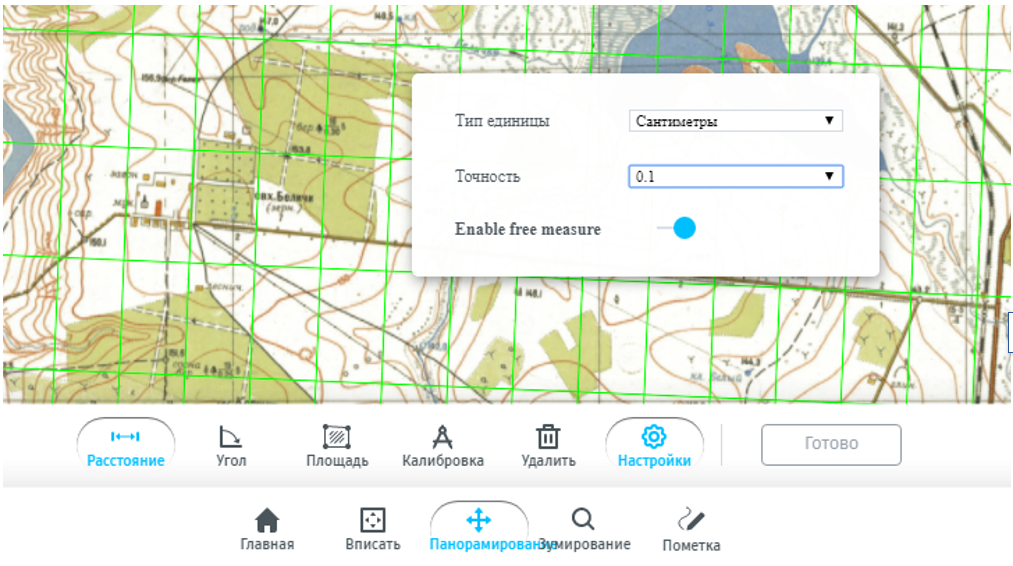
- Определить геодезические координаты точек – широту (B) и долготу (L) – с точностью до 1 секунды. Нужно выбрать инструмент Измерение (расположено на нижней панели меню). Откроется дополнительное меню для измерений. Необходимо зайти в Настройки, установить единицы измерений (сантиметры), точность (до 0,1). Обязательно подвиньте рычажок Enable free measure.
Нужно провести перпендикуляр от выбранной точки до ближайших южной и западной зеленых линий, т.е. до ближайшей южной параллели с известной широтой и ближайшего западного меридиана с известной долготой. Когда вы отметите вторую точку отрезка, появится расстояние в см. Нужно перевести расстояние в секунды, если известно, что 10-секундный отрезок по широте составляет 3,1 см, а по долготе — 1,8 см.
Заполнить таблицу 3.
| Номера точек | B (широта) | L (долгота) |
|---|---|---|
| 1 (A) | ||
| 2 (B) |
- Определить прямоугольные координаты точек – абсциссу и ординату – с точностью до 5 м.
Измерения проводить аналогично пункту 4, но перпендикуляры проводить к линиям километровой сетки. Вычислить разность соответствующих координат точек. Заполнить таблицу 2.
Номера точек Прямоугольные координаты, м
| Номера точек | X | Y |
|---|---|---|
| 1 (A) | ||
| 2 (B) | ||
| (Delta) = |
- Измерение расстояния и дирекционного угла:
Проведите измерение расстояния от 1-й до 2-й точки S в см, переведите в метры на местности, значение внесите в таблицу 4.
| Измеренный | Вычисленные | |
|---|---|---|
| Дирекционный угол ((alpha)) направления: 1-2 (A,B) | ||
| Расстояние (S) между точками: 1-2 (A-B), м |
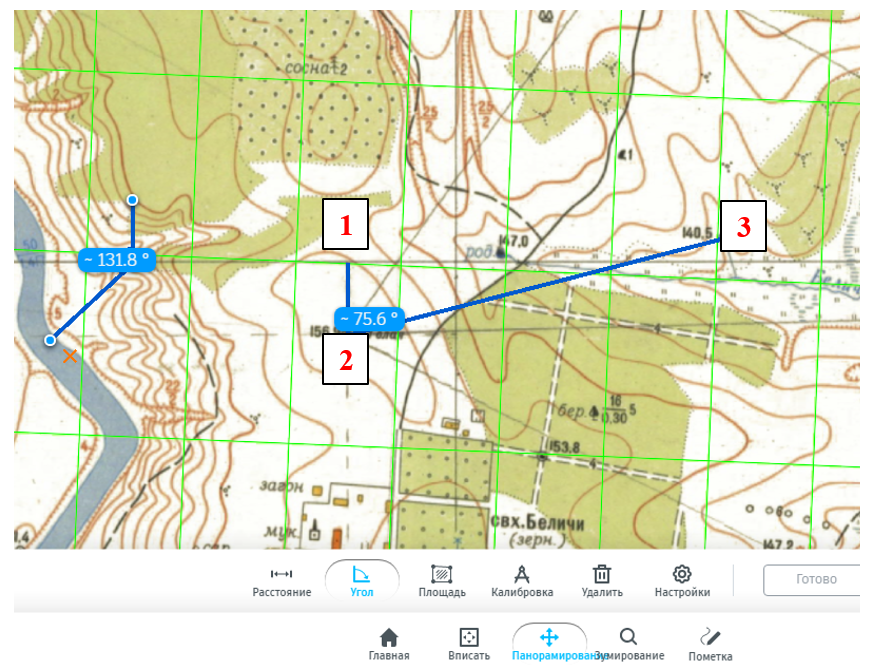
Выберите инструмент измерения углов. Чтобы измерить дирекционный угол, нужно отметить 3 точки: первая точка (1) это проекция вашей точки A на ось Y (выберите горизонтальную линию сетки севернее вашей точки, поскольку дирекционый угол считается от северного направления линии сетки (оси Х) до выбранного направления), вторая (2) — ваша точка А, третья (3) — ваша точка В.
Обратите внимание, что измерения углов в программе ведутся по часовой (от 0° до 180°) и против часовой (от 0° до 180°). Если измеряемый Вами угол больше 180°, необходимо полученное значение вычесть из 360°. На рисунке при измеренном значении 131,8° дирекционный угол будет равен 228,2°. Измеренное (или рассчитанное) значение дирекционного угла (alpha) выбранного направления нужно внести в строки таблиц 4 (измеренные) и 5.
Внимание! Измеренное значение вносится в бланк дважды и должно быть одинаковым!
-
Вычислить дирекционный угол А выбранного направления и расстояние S, решив обратную геодезическую задачу. Полученные значения округлить до до 0,5° и 1 м соответственно, данные занести в таблицу 4. Сравнить измеренные и вычисленные значения дирекционного угла и расстояния. Разность значений не должна превышать 1° для углов и 10 м для расстояний.
-
Определить, пользуясь формулами и информацией из зарамочного оформления карты, другие ориентирующие углы выбранного направления (точка 1 – точка 2), последовательно заполняя таблицу 5.
| Ориентируемая линия 1-2 (A-B) | Угол |
|---|---|
| Дирекционный угол (alpha) | |
| Сближение меридианов (gamma) | |
| Геодезический азимут A | |
| Магнитное склонение D | |
| Магнитный азимут Aм |
● Определить среднее значение Гауссова сближения меридианов (gamma) на листе карты.
● Вычислить геодезический азимут А выбранного направления.
● Вычислить величину склонения магнитной стрелки D на текущую дату.
● Вычислить магнитный азимут Am выбранного направления.
Карпачевский А.М., Каргашин П.Е., Прасолова А.И. Топография с основами геодезии. М.: Географический факультет МГУ, 2023.