Как найти координату точки пересечения медиан треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

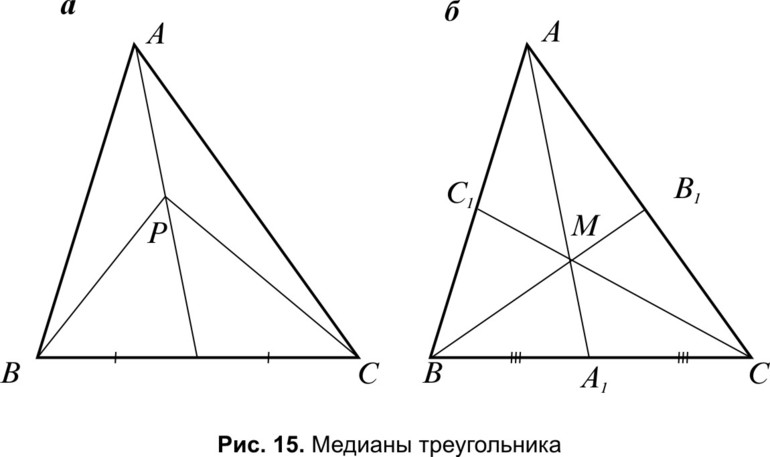
Как найти точку пересечения медиан треугольника, зная координаты его вершин?

1 способ

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

Пример.

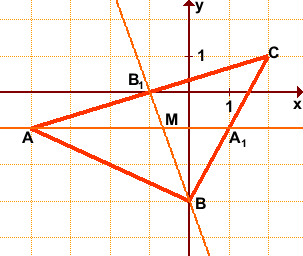
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Решение:

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

$[x_{A_1 } = frac{{x_B + x_C }}{2} = frac{{0 + 2}}{2} = 1,]$

$[y_{A_1 } = frac{{y_B + y_C }}{2} = frac{{ - 3 + 1}}{2} = - 1,]$

$[x_{B_1 } = frac{{x_A + x_C }}{2} = frac{{ - 4 + 2}}{2} = - 1,]$

$[y_{B_1 } = frac{{y_A + y_C }}{2} = frac{{ - 1 + 1}}{2} = 0.]$

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

$[left{ begin{array}{l} - 1 = k cdot ( - 4) + b, \ - 1 = k cdot 1 + b, \ end{array} right. Rightarrow k = 0,b = - 1,]$

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

$[left{ begin{array}{l} - 3 = k cdot 0 + b, \ 0 = k cdot ( - 1) + b, \ end{array} right. Rightarrow k = - 3,b = - 3,]$

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

$[left{ begin{array}{l} {rm{y = - 1}}, \ {rm{y = - 3x - 3}}{rm{,}} \ end{array} right. Rightarrow x = - frac{2}{3},y = - 1.]$

Ответ:

$[( - frac{2}{3}; - 1).]$

2 способ

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

По формулам деления отрезка в данном отношении

$[x = frac{{nx_1 + mx_2 }}{{m + n}},y = frac{{ny_1 + my_2 }}{{m + n}}]$

$[x_M = frac{{1 cdot x_A + 2 cdot x_{A_1 } }}{{2 + 1}} = frac{{1 cdot ( - 4) + 2 cdot 1}}{3} = - frac{2}{3},]$

$[y_M = frac{{1 cdot y_A + 2 cdot y_{A_1 } }}{{2 + 1}} = frac{{1 cdot ( - 1) + 2 cdot ( - 1)}}{3} = - 1.]$

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Точка пересечения медиан треугольника

Определение и точка пересечения медиан треугольника

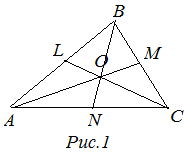
Из каждой вершины треугольника можно опустить медиану.

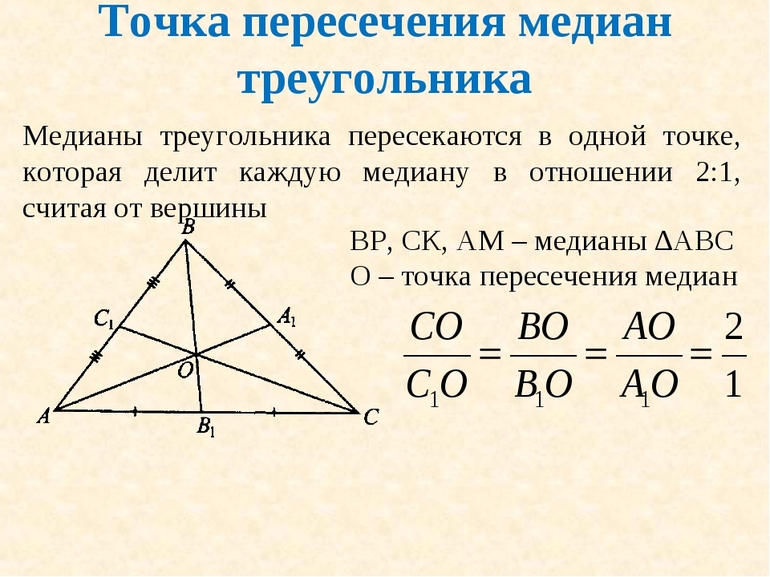
Три медианы в треугольнике пересекаются в одной точке и эту точку называют центром тяжести треугольника.

Точка пересечения медиан делит каждую медиану в отношении , считая от вершины.

Отрезки прямых, соединяющих вершины треугольника с центром тяжести, делят треугольник на три равновеликих треугольника (т.е. на треугольники с одинаковой площадью).

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

Решение

Первый способ.

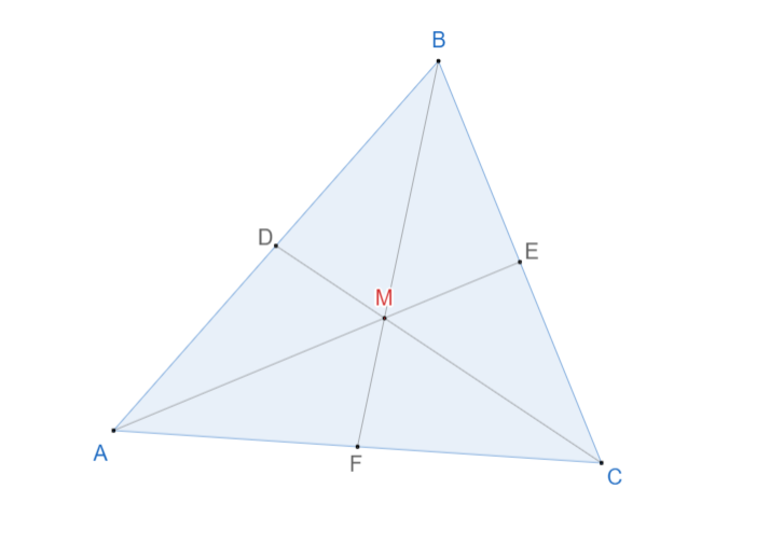
Известно, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины. Поэтому, если D(x₁;y₁) — середина отрезка BC, то AM : MD = 2 : 1. Известно также, что координаты середины отрезка есть средние арифметические соответствующих координат его концов. Значит,

x₁ = $displaystyle {frac{8-4}{2}}$ = 2, y₁ = $displaystyle {frac{-3+1}{2}}$ = — 1.

Поскольку точка M(x₀;y₀) делит отрезок AD в отношении 2:1, считая от точки A, то по теореме о пропорциональных отрезках проекция точки M на ось OX делит проекцию отрезка AD на эту ось в том же отношении, т.е.

$displaystyle {frac{x_{0}-5}{2-x_{0}}}$ = 2.

Отсюда находим, что x₀ = 3. Аналогично находим, что y₀ = 1.

Второй способ.

Пусть M(x₀;y₀) — точка пересечения медиан треугольника ABC. Поскольку координаты точки пересечения медиан треугольника есть средние арифметические соответствующих координат вершин треугольника, то

x₀ = $displaystyle {frac{5+8-4}{3}}$ = 3, y₀ = $displaystyle {frac{5-3+1}{3}}$ = 1.

Ответ

(3;1).

Источник

Как найти точку пересечения медиан

Медианой треугольника называется линия, которая проведена из его угла и делит пополам противолежащую сторону. Все медианы пересекаются в одной точке. Найти эту точку необходимо, если нужно знать, где находится центр тяжести детали, имеющей треугольную форму. Это можно сделать с помощью геометрических построений.

Вам понадобится

— треугольник с заданными параметрами;
— карандаш;
— транспортир;
— линейка;
— компьютер с программой AutoCAD.

Инструкция

Вычисления начните с геометрических построений. Постройте треугольник согласно имеющимся у вас данным. Это могут быть три стороны, сторона и два прилежащих к ней угла либо же две стороны и угол между ними. Для определения точки пересечения медиан вам необходимо знать размеры всех трех сторон, поэтому обозначьте на чертеже то, что вам известно и найдите остальные размеры.

Обозначьте треугольник как АВС. Стороны, противолежащие углам, будут соответственно, a, b и с. Проведите медианы и обозначьте их как m1, m2 и m3, а точку их пересечения — как О.

Вспомните свойство медиан. Точка пересечения отсекает от каждой из них отрезки в соотношении 2:1. Больший отрезок — тот, который ограничен вершиной угла и точкой О. Это важно, поскольку вам необходимо определить расстояние этой точки от каждого из углов.

Длину медианы, принадлежащей той или иной стороне, вычислите по формуле Стюарта. Она равна квадратному корню из дроби, числитель которой представляет собой сумму удвоенных квадратов сторон, не принадлежащих данной медиане, за вычетом из нее квадрата третьей стороны. В знаменателе подкоренного выражения стоит число 4. То есть m1 = √(2*a2+2*b2-c2)/4. Вычислите таким же образом две остальные медианы.

Обозначьте отрезки, на которые делит медиану точка пересечения, как L1 и L2. Отрезок L1 в два раза больше отрезка L2. При этом L2 = m1/3. Найдите расстояние L2. Оно равно 2*L1, то есть L2 = 2*m/3. Таким же образом найдите расстояния точки пересечения от остальных углов треугольника и его сторон.

Для определения точки пересечения медиан в AutoCAD постройте треугольник, определив координаты его вершин. Обозначьте треугольник как АBC. Найдите координату точки О по оси х. Она будет равна сумме координат х всех вершин треугольника, деленной на 3. Точно так же найдите и координату y. Для более точных расчетов пользуйтесь встроенным калькулятором.

Видео по теме

Полезный совет

В AutoCAD можно поступить и другим способом. Найдите координаты медиан. Для этого сложите одноименные координаты двух углов, принадлежащих одной стороне. Полученную сумму поделите на 2. Таким же образом найдите вторую координату. Для определения точки пересечения достаточно вспомнить свойство медианы делиться в точке пересечения в соотношении 2:1. Зная координаты угла и точки пересечения медианы со стороной, найдите эту точку. Сложите одноименные координаты и разделите их сумму на 3, поступив точно так же со второй парой.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Общие сведения

Перед доказательством теорем необходимо ознакомиться с основными понятиями. Прямой называется совокупность точек, расположенных в одной плоскости, через которые можно провести линию без искажений в пространстве. Отрезок — часть прямой, ограниченной правой и левой границами.

Треугольник (обозначается «Δ») — геометрическая фигура, состоящая из трех сторон и вершин. Предпоследние являются отрезками, а последние — точками, не лежащими на одной прямой и соединяющими стороны между собой. Следует отметить, что треугольники бывают нескольких типов. К ним относятся следующие:

Произвольный.
Равнобедренный.
Равносторонний (правильный).

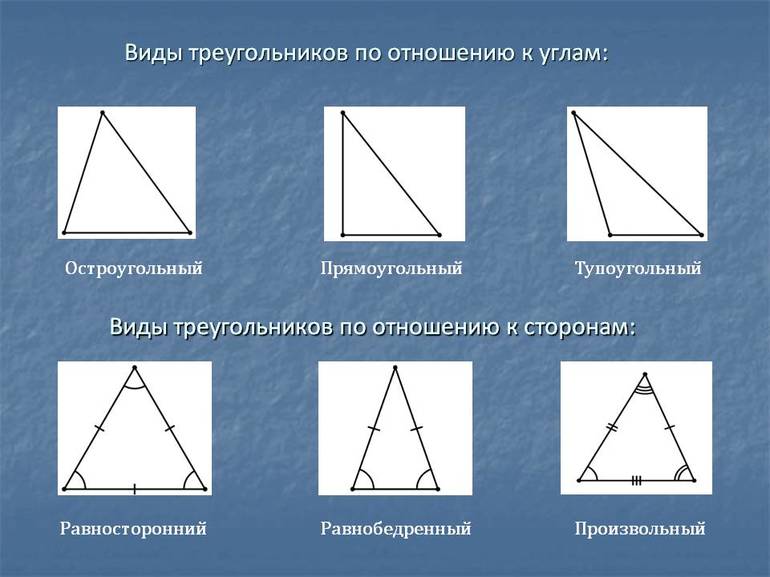
Первая группа состоит из сторон различной длины. При двух эквивалентных между собой сторонах фигура является равнобедренной. Обязательным условием для третьей группы считается равенство всех сторон. Кроме того, фигуры делятся по типу градусных мер таким образом:

Остроугольные.
Прямоугольные.
Тупоугольные.

Остроугольным называется треугольник, у которого углы (в задачах обозначается символом «∠ «) меньше 90 градусов.

Если у него один из ∠ эквивалентен 90, то этот признак свидетельствует о принадлежности его ко второму типу. Когда у фигуры хотя бы один из ∠ больше 90, тогда он принадлежит к третьему виду.

Понятие дополнительных отрезков

У любого Δ существуют дополнительные отрезки, которые используются при решении задач по геометрии. К ним относятся следующие: медиана, биссектриса и высота. Они существенно отличаются между собой в произвольных треугольниках, а также совпадают в равнобедренных и правильных геометрических телах.

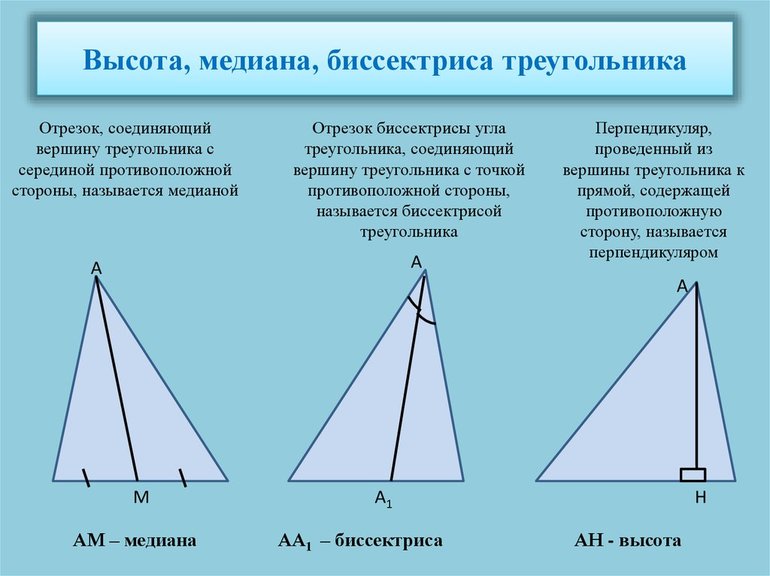
Медиана (М) — некоторый отрезок, исходящий из вершины на середину стороны. Иными словами, любой геометрический элемент, опущенный из вершины на среднюю точку, является медианой. Последних в треугольнике может быть не более трех.

Биссектриса (Б) — часть прямой, которая делит угол на два равных компонента. В любом треугольнике можно провести всего три таких отрезка. Высота (В) — перпендикуляр, опущенный из вершины на противоположную сторону. Следует отметить, что высоты бывают внешними и внутренними. Первые проводятся из вершины на проекцию Δ, а вторые находятся внутри фигуры. В каждом треугольнике можно провести определенное количество дополнительных отрезков:

Произвольный: М — 3, В — 3 и Б — 3. Все они не совпадают между собой.
Равнобедренный: М — 2, В — 2, Б — 2 и М=В=Б=1 (совпадают между собой). Всего элементов: 2+2+2+3*1=9.
Правильный: М=В=Б=3. Общее количество элементов: 3.

Во втором случае М, В и Б совпадают между собой только один раз, а в последнем — полное сходство, поскольку медианы являются биссектрисами и высотами. Их точка пересечения — центр треугольника. Далее следует перейти к непосредственному доказательству теорем.

Теорема о взаимном пересечении

Первую базовую теорему, которую следует разобрать, имеет такую формулировку: медианы любого треугольника пересекаются в одной точке, которая является центром фигуры. Ее доказательство осуществляется по такому алгоритму:

Начертить произвольный ΔSTU. Провести в нем медианы SS’ и TT’. Обозначить точку их пересечения «F».
Доказывать утверждение нужно от противного, т. е. предположить, что медианы не пересекаются, т. е. являются параллельными отрезками (SS’||TT’).
Из этого утверждения следует, что сторона фигуры ST является их секущей.
Следовательно, ∠S+∠T=360. Однако это противоречит свойству градусных мер углов треугольника, которые должны быть не более 180. Исходя из этого, предыдущая гипотеза не подтверждается.
На основании вывода из четвертого пункта теорема доказана полностью.

Аналогично можно доказать, что медиана UU’ также пересекается с SS’ и TT’ в точке F. Для этой цели необходимо начертить еще один треугольник с таким же обозначением, т. е. ΔSTU.

После этого выполнить все пять пунктов алгоритма, но для медиан SS’ и UU’. Затем сопоставить два доказательства для получения общей формулировки.

Утверждения о соотношении

Однако для решения задач одной теоремы о пересечении медиан недостаточно. Математики доказали несколько других утверждений, которые могут быть полезными при нахождении неизвестных величин. Первая из них гласит, что точка, в которой пересекаются медианы, пропорционально делит медианы 2:1 относительно вершины. Для доказательства утверждения необходимо воспользоваться такой методикой:

Начертить ΔSTU и провести в нем SS’ и UU’, обозначив их пересечения точкой «F».
Из точек S’ и U’ опустить отрезки на SF и UF так, чтобы разделить их на две равные части (U» и S»).
В результате операций, выполненных во втором пункте, получился четырехугольник. Его сторона U’S’ является средней линией ΔSTU, т. е. U’S’||SU и U’S’=0,5SU.
Сторона U»S» — средняя линия ΔSFU, т. е. U»S»||SU и U»S»=1/2(SU).
Из третьего и четвертого пунктов можно сделать вывод, что U’S’U»S» — параллелограмм, у которого диагонали пересекаются в точке и делятся на две равные части.
Выполнив анализ информации, полученной на пятом шаге, можно завершить доказательство теоремы, т. к. диагонали параллелограмма делятся в пропорциональном соотношении 2:1.

Следующим полезным утверждением является формула, позволяющая найти длину медианы. Она в словесном эквиваленте звучит таким образом: длина равна квадратному корню из суммы половины квадратов двух других сторон, не принадлежащих ей, без четвертой части квадрата стороны, на которую она опущена. Для доказательства рекомендуется использовать такой алгоритм:

Начертить ΔSTU с медианой SS’=М{u} (опущена на UT), обозначив его стороны s=US, t=ST и u=UT.
По свойству медианы: US’=0.5*UT.
Образовались два треугольника ΔUSS’ и ΔTSS’.
Для нахождения M необходимо к каждому Δ применить теорему косинусов. В результате этого получатся такие соотношения: s^2=M{u}^2+(u/2)^2-2M{u}(u/2)cos(∠U) и t^2=M{u}^2+(u/2)^2-2M{u}(u/2)cos(Pi-∠U).
Выполняя математические операции по раскрытию скобок и складывая между собой полученные соотношения, получается искомая формула: M{u}=[(s^2)/2 + (t^2)/2 — (u^2)/4]^(1/2).
Утверждение доказано.

Теорема имеет следствие, представленное в виде соотношения, позволяющее выявить взаимосвязь между сторонами и медианами. Оно имеет такой вид: (М{u})^2 + (М{s})^2 + (М{t})^2=3/4(s^2+t^2+u^2).

Координаты точки

При решении задач очень часто необходимо находить координаты точки пересечения медиан произвольного ΔSTU. Доказательство или выведение этой формулы является очень сложным. Однако математики решили данную проблему. Они предлагают использовать уже готовое соотношение, состоящее из двух компонентов:

Ордината: Y=[(М{u})^2+(М{s}+М{t}^2 — 2М{u}М{s}М{t}]^(1/2)=[(s+t)^2+u^2 — 2((s*t*u)/(s*t*u))]^(1/2).
Абсцисса: X=[((М{u})^2+(М{s}+М{t}^2)/(2М{u}М{s}М{t})]^(1/2)=[((s+t)^2+u^2)/(2((s*t*u)/(s*t*u)))]^(1/2).

Вышеописанные формулы рекомендуется применять, когда требуется определить координаты точек без чертежа. Специалисты на ранних этапах обучения рекомендуют размещать треугольник в прямоугольной декартовой системе координат. После этого отмечать каждую вершину с заданными координатами, а затем проводить медианы.

Для нахождения величины абсциссы и ординаты нужно из искомой точки опускать перпендикуляры на последние.

Нахождение координаты будет очень простым и удобным. Кроме того, в интернете существует множество приложений для этих целей. Они называются онлайн-калькуляторами.

Иногда встречаются задания со следующей формулировкой: выведите формулы, выражающие координаты точки пересечения медиан, с исходными данными (вершинами или сторонами). Для этого рекомендуется просто подставить искомые значения в соответствующие формулы нахождения абсциссы и ординаты.

Полезные свойства

Математики для облегчения учебы вывели важные свойства медианы. К ним относятся следующие:

Точка пересечения является центром вписанной и описанной окружностей, почему ее еще и называют симметрией фигуры.
Точки соприкосновения медиан со сторонами образуют средние линии искомого треугольника. Их всего три.
Подобие фигур относительно исходной.
Медианы делят произвольный треугольник на шесть подобных.
Отрезок, опущенный на гипотенузу, делит ее на два радиуса описанной окружности.

На координатной плоскости, руководствуясь первым свойством, чертится треугольник. После этого требуется провести две медианы, обозначив общую точку (где они пересекаются). Далее необходимо поставить в нее иголку циркуля, и начертить окружность вокруг фигуры. Затем в искомом круге проводится диаметр D.

В результате у вписанной окружности величина радиуса должна соответствовать значению D/4. На основании этого необходимо полагать, что построение выполнено правильно. В противном случае допущена некоторая неточность.

Используя второе свойство, можно найти следующие параметры: площадь, стороны и другие элементы фигуры. В любых задачах допускается подобное дополнительное построение. Однако специалисты рекомендуют его применять только при необходимости, а не загромождать чертеж.

Третье и четвертое свойства применяются для подсчета площадей подобных фигур. Коэффициент подобия зависит от количества проведенных медиан:

Одна: 1:0,75.
Две: 1:3,2.
Три: 1:6.

Последние цифры являются коэффициентом подобия. В прямоугольном треугольнике медиана, опущенная из прямого угла, делит ее на две равные части-радиусы описанной окружности.

Таким образом, сведения о медианах в треугольнике расширяет возможности расчета некоторых параметров фигуры.

Источник