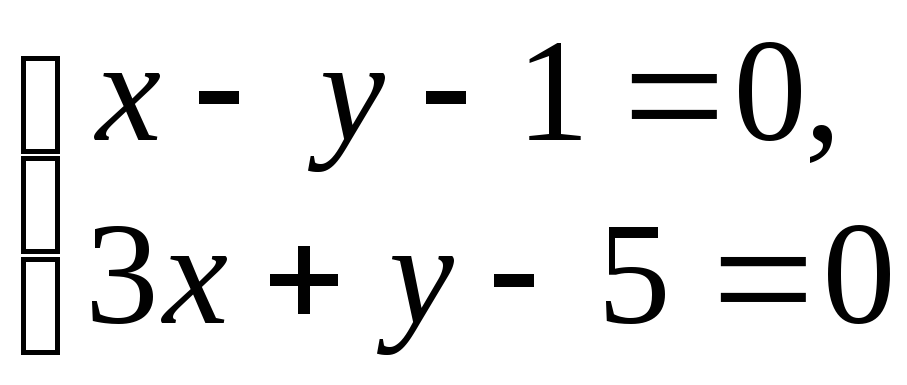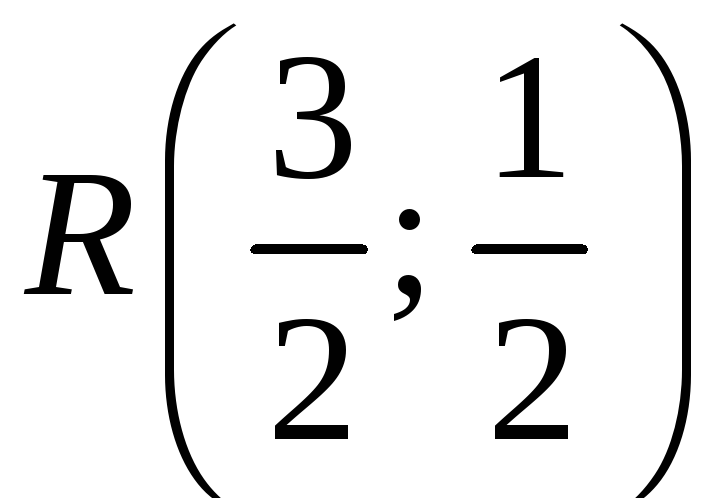Решение
Найдём уравнение прямой BC по двум точкам:

, или y = —
x — 6.
Тогда её угловой коэффициент k1 = — . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = — 1. Поэтому
k2 = — = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; — 1) и угловому коэффициенту k2 = 2:
y + 1 = 2(x — 5), или y = 2x — 11.
Найдём уравнение прямой AC по двум точкам:

, или y =
x —
.
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = — 1. Поэтому
k4 = — = — 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; — 
y + 8 = — 3(x — 4), или y = — 3x + 4.
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Получим: x = 3, y = — 5.

Ответ
(3; — 5).
Как найти координаты пересечения высот в треугольнике
Линия, проведенная из вершины треугольника перпендикулярно к противоположной стороне, называется его высотой. Зная координаты вершин треугольника, можно найти его ортоцентр — точку пересечения высот.

Инструкция
Рассмотрите треугольник с вершинами A, B, C, координаты которых, соответственно (xa, ya), (xb, yb), (xc, yc). Проведите высоты из вершин треугольника и обозначьте точку пересечения высот как точку О с координатами (x, y), которые и необходимо найти.
Составьте уравнение сторон треугольника. Сторона AB выражается уравнением (x−xa)/(xb−xa)=(y−ya)/(yb−ya). Приведите уравнение к виду y=k×x+b: x×yb−x×ya−xa×yb+xa×ya=y×xb−y×xa−ya×xb+ya×xa, что равносильно y=((yb−ya)/(xb−xa))×x+xa×(ya−yb)/(xb−xa)+ya. Обозначьте угловой коэффициент k1=(yb−ya)/(xb−xa). Аналогичным образом найдите уравнение любой другой стороны треугольника. Сторона AC задается формулой (x−xc)/(xa−xc)=(y−yc)/(ya−yc), y=((ya−yc)/(xa−xc))×x+xc×(ya−yc)/(xc−xa)+ya. Угловой коэффициент k2=(yc−yb)/(xc−xb).
Запишите уранение высот треугольника, проведенных из вершин B и C. Так как высота, выходящая из вершины B, будет перпендикулярна стороне AС, то ее уравнение будет иметь вид y−ya=(-1/k2)×(x−xa). А высота, проходящая перпендикулярно стороне AB и выходящая из точки C, будет выражаться в виде y−yc=(-1/k1)×(x−xc).
Найдите точку пересечения двух высот треугольника, решив систему из двух уравнений с двумя неизвестными: y−ya=(-1/k2)×(x−xa) и y−yb=(-1/k1)×(x−xb). Выразите переменную y из обоих уравнений, приравняйте эти выражения и решите уравнение относительно x. А затем подставьте полученное значение x в одно из уравнений и найдите y.
Рассмотрите для наилучшего понимания вопроса пример. Пусть дан треугольник с вершинами A (-3, 3), B (5, -1) и C (5, 5). Составьте уравнение сторон треугольника. Сторона AB выражается по формуле (x+3)/(5+3)=(y−3)/(-1−3) или y=(-1/2)×x+3/2, то есть k1=-1/2. Сторона AC задается уравнением (x+3)/(5+3)=(y−3)/(5−3), то есть y=(1/4)×x+15/4. Угловой коэффициент k2=1/4. Уравнение высоты, выходящей из вершины C: y−5=2×(x−5) или y=2×x−5, а высоты, выходящей из вершины B: y−5=-4×(x+1), что есть y=-4×x+19. Решите систему из этих двух уравнений. Получается, что ортоцентр имеет координаты (4, 3).
Источники:
- Основные линии треугольника
- найти координаты точки на стороне треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
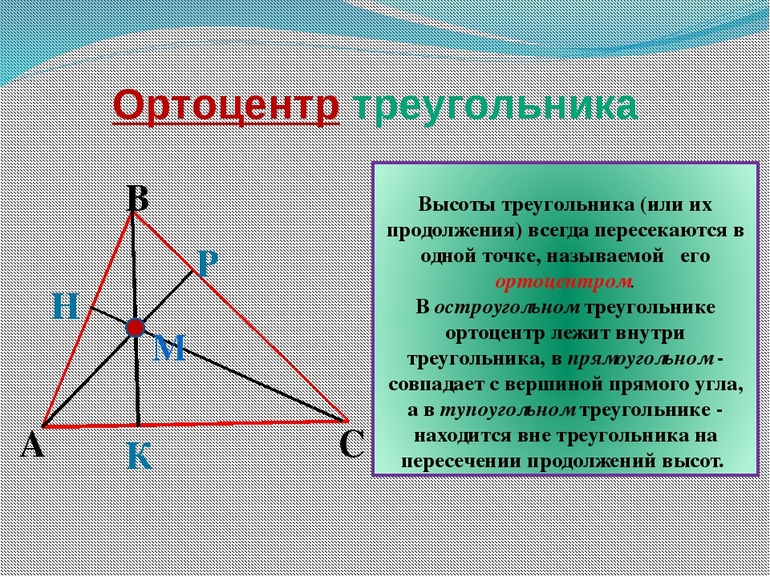
Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра
Что такое высота
Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.
Свойства ортоцентра
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.
Ортоцентр по отношению к фигуре может быть расположен:
- внутри;
- снаружи;
- в вершине (у прямоугольных треугольников)
Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.
Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:
Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
Полезные факты
Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.
Пусть:
- H — ортоцентр в ABC;
- О — центр описанной окружности.
Тогда:
- окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
- отрезок BH вдвое длиннее отрезка АС;
- середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.
Задача Фаньяно
Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.
Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.
Площадь ортотреугольника рассчитывается по формуле:
Здесь S — площадь, а, b, c — стороны.
Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.
История изучения
Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».
Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.
В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.
Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.
Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.
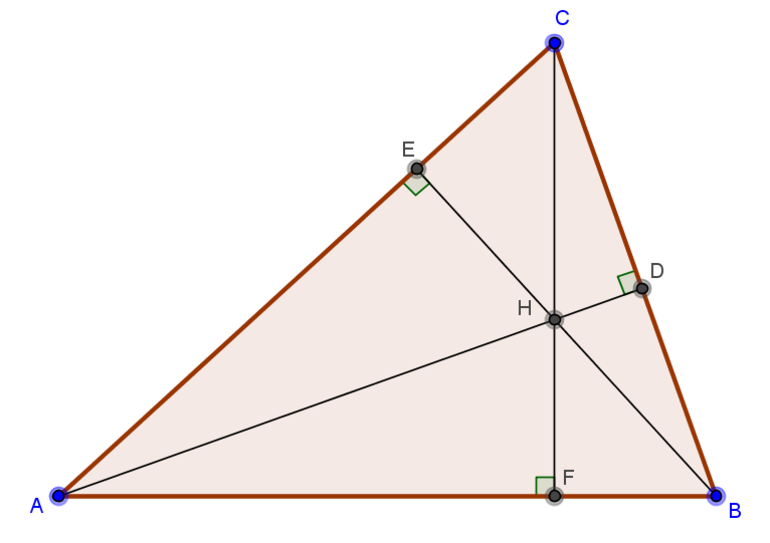
Ортоцентр треугольника
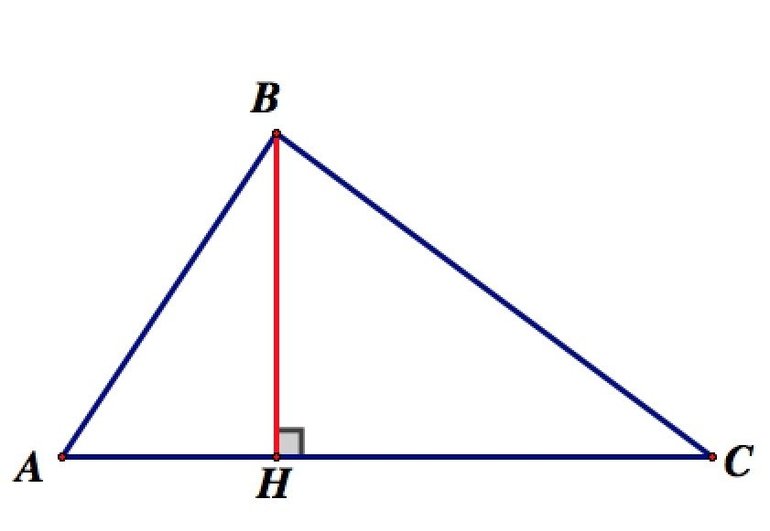
Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).
Пример
В приведенном ниже примере, O это ортоцентр..
Метод расчета ортоцентра треугольника
Пускай даны точки треугольника A(4,3), B(0,5) и C(3,-6).
Шаг 1
Найдем наклоны сторон AB, BC и CA используя формулу y2-y1/x2-x1. Наклон обозначим ‘m’.
- Наклон AB (m) = 5-3/0-4 = -1/2.
- Наклон BC (m) = -6-5/3-0 = -11/3.
- Наклон CA (m) = 3+6/4-3 = 9.
Шаг 2
Теперь, давайте вычислим наклон высоты AD, BE и CF который перпендикулярен сторонам BC, CA и AB соответственно. Наклон высоты = -1/наклон противоположной стороны треугольника.
- Наклон AD = -1/наклон BC = 3/11.
- Наклон BE = -1/наклон CA = -1/9.
- Наклон CF = -1/наклон AB = 2.
Шаг 3
После того, как мы нашли наклон перпендикуляров, мы должны найти уравнение линий AD, BE и CF. Давайте найдем уравнение линии AD с точкой (4,3) и наклоном 3/11.
Формула, для нахождения уравнения ортоцентра треугольника = y-y1 = m(x-x1) y-3 = 3/11(x-4)
1) Упростив выше приведенное уравнение, мы получим 3x-11y = -21
Кроме того, мы должны найти уравнение линий BE и CF. Уравнение для линии BE с точкой (0,5) и наклоном -1/9 = y-5 = -1/9(x-0)
2) Упростив выше приведенное уравнение, мы получим x + 9y = 45
Уравнение для линии CF с точкой (3,-6) и наклоном 2 = y+6 = 2(x-3)
3) Упростив выше приведенное уравнение, мы получим 2x — y = 12
Шаг 4
Найдем значение x и y решив 2 любых из 3 уравнений.
В этом примере, значение x и y (8.05263, 4.10526) которые являются координатами Ортоцентра (o).
Даны точки A(5; — 1), B(4; — 8), C(- 4; — 4). Найдите координаты точки пересечения высот треугольника ABC.
Найдём уравнение прямой BC по двум точкам:
= , или y = — x — 6.
Тогда её угловой коэффициент k1 = — . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = — 1. Поэтому
k2 = — = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; — 1) и угловому коэффициенту k2 = 2:
Найдём уравнение прямой AC по двум точкам:
= , или y = x — .
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = — 1. Поэтому
k4 = — = — 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; — 
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Ответ
http://wpcalc.com/ortocentr-treugolnika/
http://gitun.com/q/18151
Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.
Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.
Первое , что необходимо найти наклон сторон, который обозначается — m , используется формула :
Из этого следует:
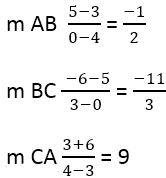
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:
Имеем:
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
y-y1 = m(x-x1) y-3 = 3/11(x-4)
С помощью упрощения, имеем: 3х — 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем 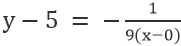
Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.
Раздел V.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
В раздел включены
задачи, которые рассматриваются в теме
«Аналитическая геометрия на плоскости
и в пространстве»: составление различных
уравнений прямых на плоскости и в
пространстве; определение взаимного
расположения прямых на плоскости,
прямых, прямой и плоскости, плоскостей
в пространстве; изображение кривых
второго порядка. Необходимо отметить,
что в данном разделе представлены задачи
экономического содержания, при решении
которых применяются сведения из
аналитической геометрии на плоскости.
При решении задач
аналитической геометрии целесообразно
воспользоваться учебными пособиями
следующих авторов: Д.В. Клетеника, Н. Ш.
Кремера, Д.Т. Письменного В.И. Малыхина,
т.к. в данной литературе рассматривается
более широкий круг задач, которые можно
использовать для самостоятельной
подготовки по данной теме. Применение
аналитической геометрии к решению
экономических задач изложено в учебных
изданиях М.С. Красса и В.И. Ермакова.
Задача 5.1. Даны
координаты вершин треугольника АВС.
Необходимо
а) написать
уравнения сторон треугольника;
б) написать
уравнение высоты треугольника проведенной
из вершины С
к стороне АВ
и найти ее длину;
в) написать
уравнение медианы треугольника,
проведенной из вершины В
к стороне АС;
г) найти углы
треугольника и установить его вид
(прямоугольный, остроугольный,
тупоугольный);
д) найти длины
сторон треугольника и определить его
тип (разносторонний, равнобедренный,
равносторонний);
е) найти координаты
центра тяжести (точка пересечения
медиан) треугольника АВС;
ж) найти координаты
ортоцентра (точка пересечения высот)
треугольника АВС.
К каждому из
пунктов а) – в) решения сделать рисунки
в системе координат. На рисунках
обозначить соответствующие пунктам
задачи линии и точки.
Данные к условию
задачи, соответствующие вариантам:
|
1)
2)
3)
7)
9)
10)
11)
12)
13)
14)
15)
16)
17) 18) |
4)
5)
6)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29) 30) |
Пример 5.1
Даны координаты
вершин треугольника АВС:
.
Необходимо а) написать уравнения сторон
треугольника; б) написать уравнение
высоты треугольника проведенной из
вершины С
к стороне АВ
и найти ее длину; в) написать уравнение
медианы треугольника, проведенной из
вершины В
к стороне АС;
г) найти длины сторон треугольника и
определить его тип (разносторонний,
равнобедренный, равносторонний); д)
найти углы треугольника и установить
его вид (прямоугольный, остроугольный,
тупоугольный); е) найти координаты центра
тяжести (точка пересечения медиан)
треугольника АВС;
ж) найти координаты ортоцентра (точка
пересечения высот) треугольника АВС.
Решение
а)
Для каждой стороны треугольника известны
координаты двух точек, которые лежат
на искомых линиях, значит уравнения
сторон треугольника – уравнения прямых,
проходящих через две заданные точки
|
|
(5.1) |
где
и
соответствующие координаты точек.
Таким образом,
подставляя в формулу (5.1) координаты
соответствующих прямым точек получаем
,
,
,
откуда после
преобразований записываем уравнения
сторон
,
,
.
На рис. 7 изобразим
соответствующие сторонам треугольника
прямые.
Ответ:
,
,
.
|
Рис. 7 |
б)
Пусть
– высота, проведенная из вершины
к стороне
.
Поскольку
проходит через точку
перпендикулярно вектору
,
то составим уравнение прямой по следующей
формуле
|
|
(5.2) |
где
– координаты вектора перпендикулярного
искомой прямой,
– координаты точки, принадлежащей этой
прямой. Найдем координаты вектора,
перпендикулярного прямой
,
и подставим в формулу (5.2)
,
,
,
,
.
Найдем длину высоты
CH
как расстояние от точки
до прямой
|
|
(5.3) |
где
– уравнение прямой
,
– координаты точки
.
В предыдущем пункте
было найдено
.
Подставив данные
в формулу (5.3), получим
,
На рис. 8 изобразим
треугольник и найденную высоту СН.
Ответ:
.
|
Р |
в)
медиана
треугольника
делит сторону
на две равные части, т.е. точка
является серединой отрезка
.
Исходя из этого, можно найти координаты
точки
|
|
(5.4) |
где
и
– координаты соответственно точек
и
,
подставив которые в формулы (5.4), получим
;
.
Уравнение медианы
треугольника
составим как уравнение прямой, проходящей
через точки
и
по формуле (5.1)
,
.
Ответ:
(рис. 9).
|
Р |
г)
Длины сторон треугольника найдем как
длины соответствующих векторов, т.е.
,
,
.
Стороны
и
треугольника
равны, значит, треугольник является
равнобедренным с основанием
.
Ответ:
треугольник
равнобедренный с основанием
;
,
.
д)
Углы треугольника
найдем как углы между векторами,
исходящими из соответствующих вершин
данного треугольника, т.е.
,
,
.
Поскольку треугольник
равнобедренный с основанием
,
то
,
Углы между векторами
вычислим по формуле (4.4), для которой
потребуются скалярные произведения
векторов
,
.
Найдем координаты
и модули векторов, необходимых для
вычисления углов
,
;
,
,
.
Подставляя
найденные данные в формулу (4.4), получим
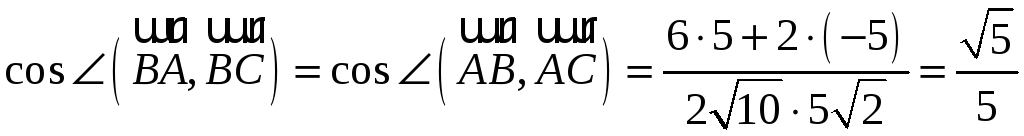
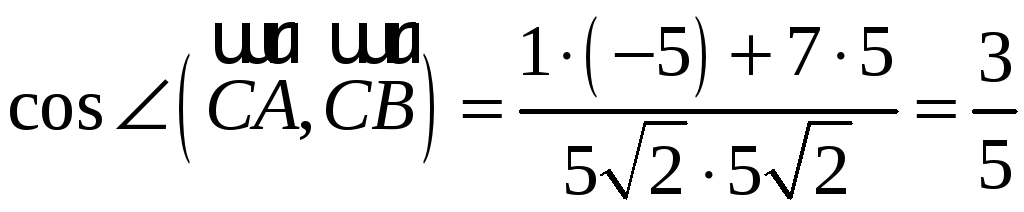
Поскольку значения
косинусов всех найденных углов
положительны, то треугольник
является остроугольным.
Ответ:
треугольник
остроугольный;
,
,
.
е)
Пусть
– центр тяжести треугольника
,
тогда координаты
точки
можно найти, по формулам (5.5)
|
|
(5.5) |
где
,
и
– координаты соответственно точек
,
и
,
следовательно,
,
.
Ответ:
– центр тяжести треугольника
.
ж) Пусть
– ортоцентр треугольника
.
Найдем координаты точки
как координаты точки пересечения высот
треугольника. Уравнение высоты
было найдено в пункте б).
Найдем уравнение высоты
:
,
,
,
.
Поскольку
,
то решение системы
является координатами
точки
,
откуда находим

Ответ:
– ортоцентр треугольника
.
Задача 5.2.
Фиксированные издержки на предприятии
при выпуске некоторой продукции
составляют F
руб. в месяц, переменные издержки – V0
руб. за
единицу продукции, при этом выручка
составляет R0
руб. за единицу изготовленной продукции.
Составить функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;

;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
.
Пример 5.2
Фиксированные
издержки на предприятии при выпуске
некоторой продукции составляют
руб. в месяц, переменные издержки –
руб. за единицу
продукции, при этом выручка составляет
руб. за единицу
изготовленной продукции. Составить
функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Решение
Вычислим совокупные
издержки на производстве при выпуске
q
единиц некоторой продукции
.
Если будет продано
q
единиц продукции, то совокупный доход
составит
.
Исходя из полученных
функций совокупного дохода и совокупных
издержек, найдем функцию прибыли
,
,
.
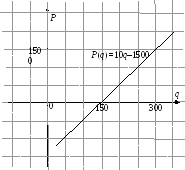
безубыточности – точка, в которой
прибыль равна нулю, или точка, в которой
совокупные издержки равны совокупному
доходу
,
,
откуда находим
– точка безубыточности.
Для построения
графика (рис. 10) функции прибыли найдем
еще одну точку
.
Рис. 10
Ответ:
функция прибыли
,
точка безубыточности
.
Задача 5.3. Законы
спроса и предложения на некоторый товар
соответственно определяются уравнениями
p=pD(q),
p=pS(q),
где p
– цена на товар, q
– количество товара. Предполагается,
что спрос определяется только ценой
товара на рынке pС,
а предложение – только ценой pS,
получаемой поставщиками. Необходимо
а) определить
точку рыночного равновесия;
б) точку равновесия
после введения налога, равного t.
Определить увеличение цены и уменьшение
равновесного объема продаж;
в) найти субсидию
s,
которая приведет к увеличению объема
продаж на q0
ед. относительно изначального
(определенного в пункте а));
г) найти новую
точку равновесия и доход правительства
при введении налога, пропорционального
цене и равного N%;
д) определить,
сколько денег будет израсходовано
правительством на скупку излишка при
установлении минимальной цены, равной
p0.
К каждому пункту
решения сделать рисунок в системе
координат. На рисунке обозначить
соответствующие пункту задачи линии и
точки.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;

;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


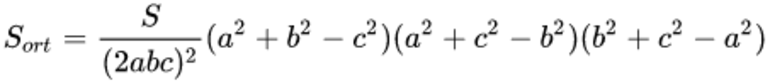

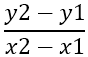
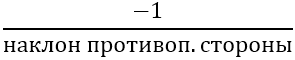
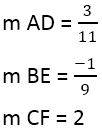

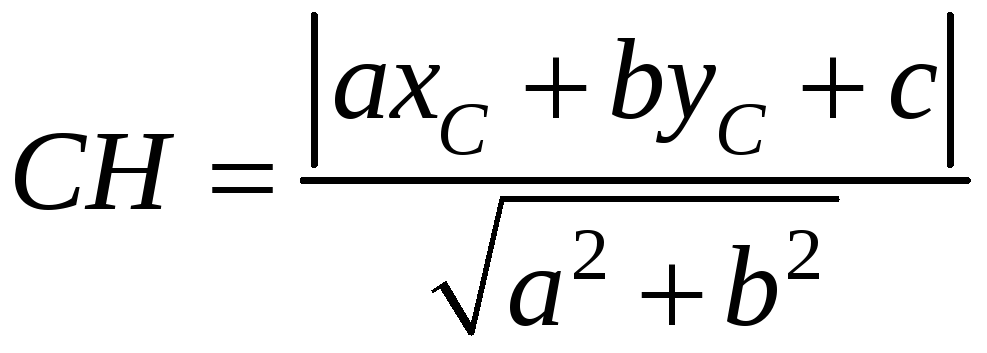 ,
, ис.
ис.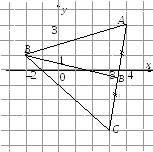 ис.
ис.