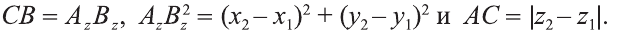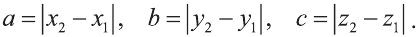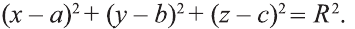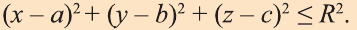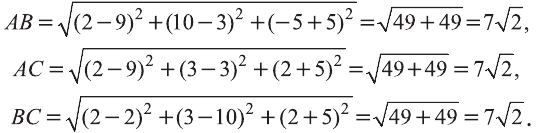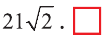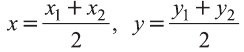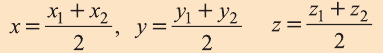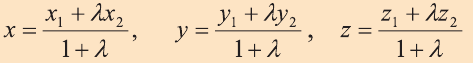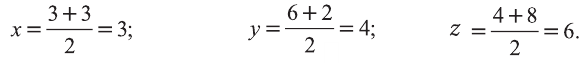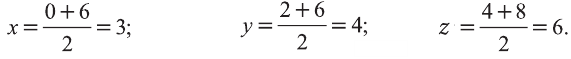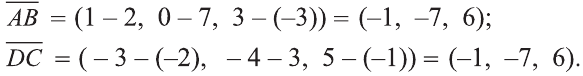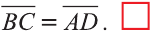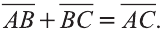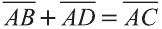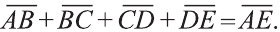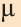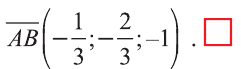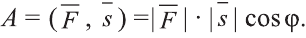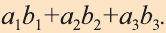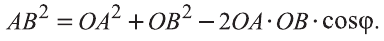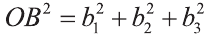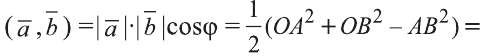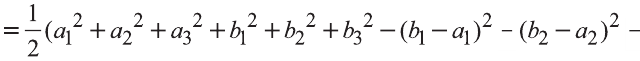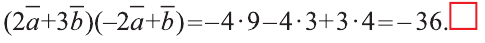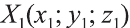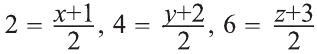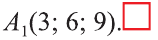Содержание:
Система координат в пространстве
Декартова система координат в пространстве
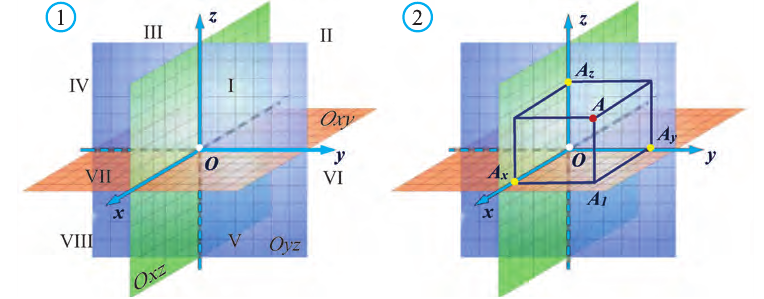
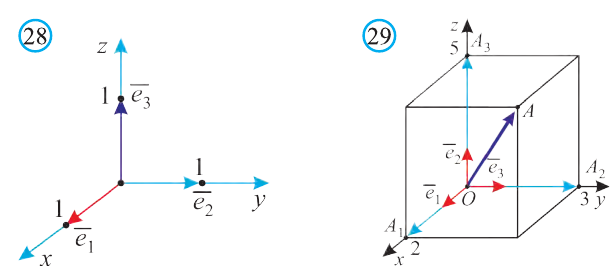
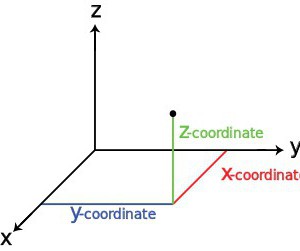
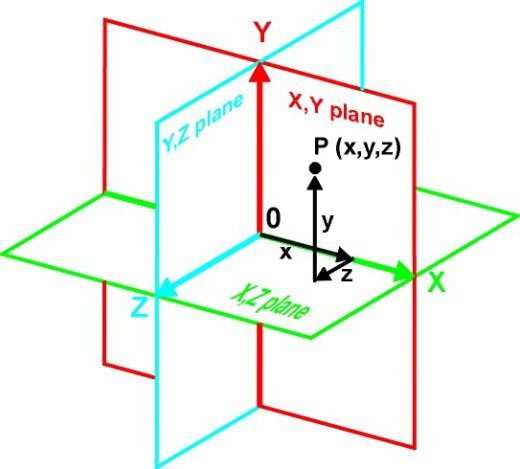
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом
точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.
Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).
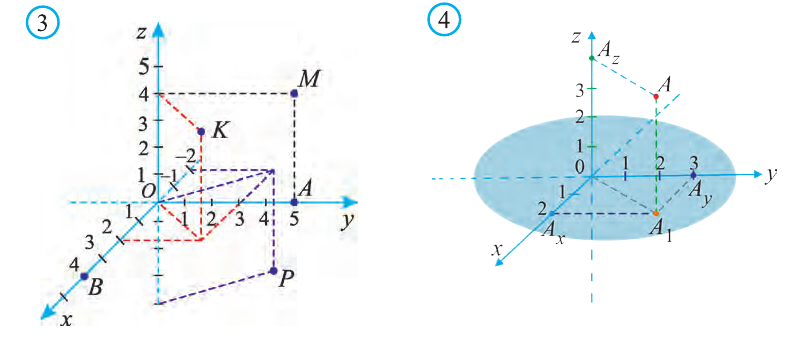
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.
Координату Ах на оси Ох называют координатой х или абсциссой точки А.
Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.
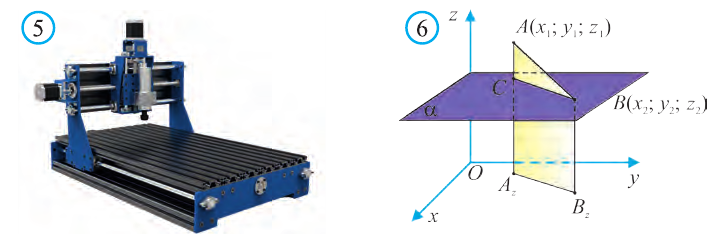
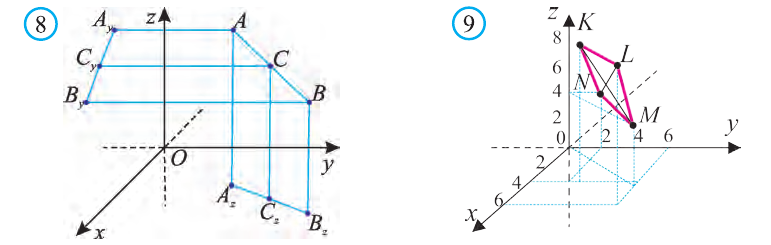
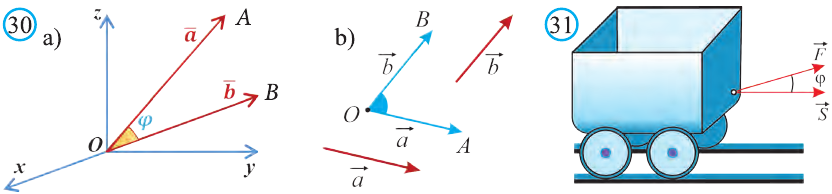
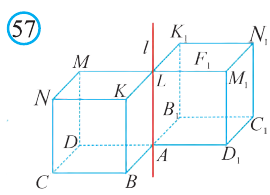
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).
Пример:
Пусть в пространстве в декартовой системе координат
задана точка А (2; 3; 4). Где она расположена?
Решение:
От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОАх = 2 и ОАу = 3 (рис. 4).
Через точку Ах проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A1 . Через точку A1 проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА1 = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.
Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).
Расстояние между двумя точками
Пусть заданы две точки А (х1; у1; z1) и B (х2; у2; z2).
1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках Аz и Вz .
Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.
Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую ААz в некоторой точке С.
По теореме Пифагора: АВ2 = АС2 + СВ2.
Однако
Поэтому
2.Пусть отрезок АВ параллелен оси Оz, тогда 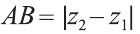
х1= х2 , у1 = у2 , мы опять приходим к вышеприведённой формуле.
Следовательно, расстояние между двумя точками А и В:
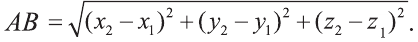
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны
Уравнение сферы и шара
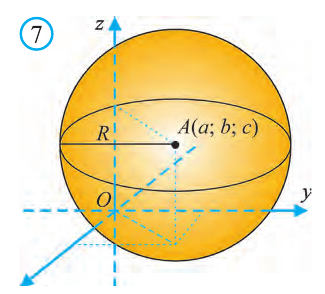
Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству
Отсюда, ясно, что неравенство для точек шара радиуса R с центром в
точке А (а; b; с) имеет вид:
Пример:
Найдите периметр треугольника ABC с вершинами в
точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).
Решение:
Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 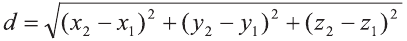
Следовательно, треугольник ABC равносторонний и его периметр 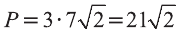
Ответ:
Координаты середины отрезка
Пусть А (x1; y1;z1) и В (х2; у2; z2) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках 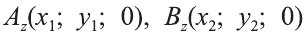
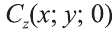
Отсюда по формулам нахождения координат середины отрезка на плоскости
Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.
Тогда и для z получим формулу, подобную вышеприведённой.
Аналогично, используя координаты концов A и B отрезка AB, по формулам
находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).
Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; 
Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.
Координаты середины отрезка МК:
Координаты середины отрезка NL:
Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.
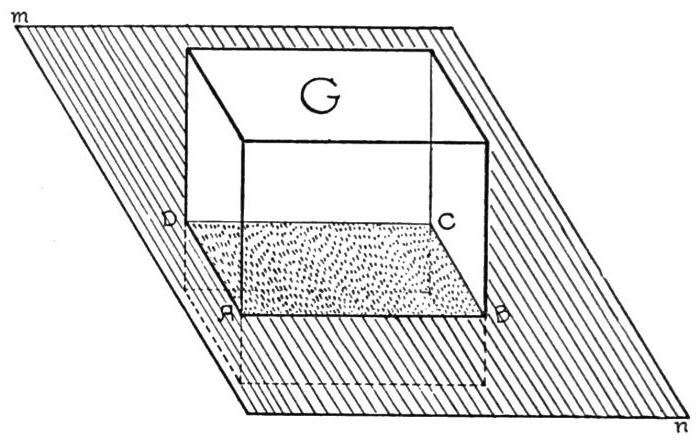
В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»
Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».
Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».
В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»
В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.
Векторы в пространстве и действия над ними
Векторы в пространстве
Понятие вектора в пространстве вводят также как на плоскости.
Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.
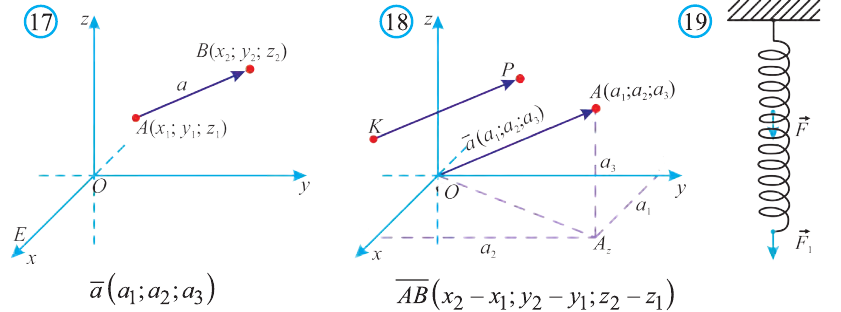
Координатами вектора с началом в точке А (х1; у1; z1) и концом в точке В (х1; у1; z1) называют числа 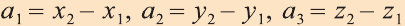
Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.
Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.
Hа основании этого вектор можно обозначить как 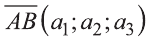
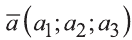
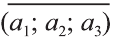
Вектор можно записать и без координат 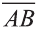
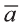
на первом месте начало вектора, а на втором — конец.
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают 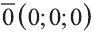
Если начало вектора расположено в начале координат О, а числа а1,
а2 и а3 — координаты точки А, то есть А (а1; а2; а3), то эти же числа будут
координатами вектора 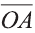
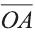
Однако вектор в пространстве 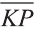
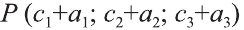
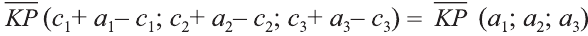
Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.
Длинной вектора называют длину направленного отрезка
изображающего его (рис. 17). Длину вектора 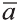
так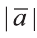
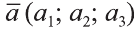
вычисляется по формуле 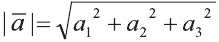
Пример:
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов 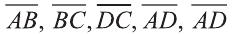
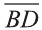
Решение:
У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:
Следовательно, 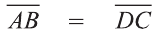
Докажите самостоятельно, что
Действия над векторами в пространстве
Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.
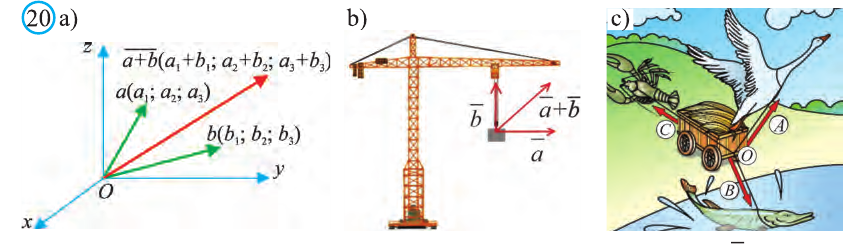
Суммой векторов 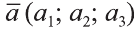

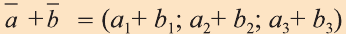
Пусть кран на рисунке 20.b движется вдоль вектора 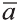
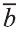
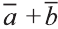
Свойства суммы векторов
Для любых векторов 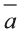
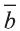
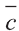
a)
b)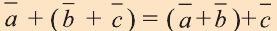
Правило треугольника сложения векторов
Для любых точек А, В и С (рис. 21):
Правило параллелограмма сложения векторов
Если АВСD — параллелограмм (рис. 22), то
Правило многоугольника сложения векторов
Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то
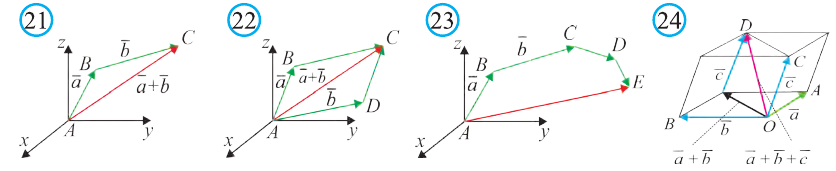
Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА1В1С1D1 параллелепипед (рис. 24), то
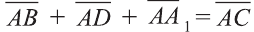
Вектор 




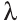
Для любых векторов 

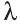
а)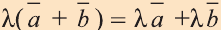
b)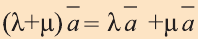
c)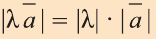
совпадает с направлением вектора 
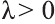
противоположно направлению вектора 
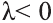
Коллинеарные и компланарные векторы
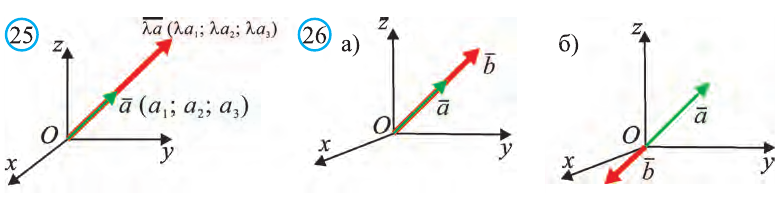
Пусть заданы ненулевые векторы 
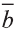


то их называют коллинеарными векторами (рис. 26).
Свойство 1. Если для векторов 

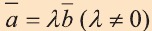
Если 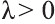



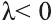
противоположно направлены 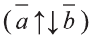
Свойство 2. Если векторы 

то их соответствующие координаты пропорциональны:
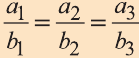
Пример:
Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору 
Решение:
Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 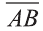
По условию задачи векторы 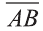

Тогда получаем следующие пропорции 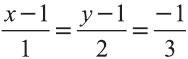
Откуда находим 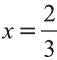
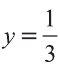
Итак,
Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).
Векторы 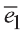
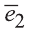
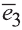
Любой вектор 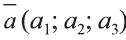
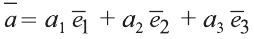
Точно также, если заданы три нeкомпланарных вектора 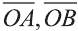
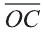
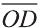
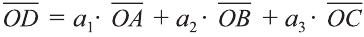
Здесь 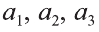
Скалярное произведение векторов
Углом между ненулевыми векторами 

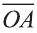

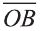

Угол между векторами 

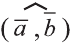
Скалярным произведением векторов 

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.
Скалярное произведение обозначают 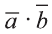
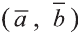
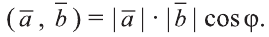
Из определения следует, что если скалярное произведение векторов 

В физике работа A, выполненная при движении тела на расстоянии 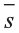
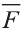
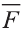
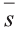
Свойство. Если 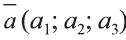


Доказательство. Приложим векторы 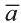

координат О (рис.32). Тогда 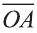
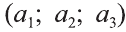
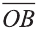
Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.
Тогда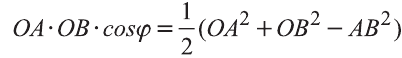
Однако, 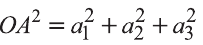
и 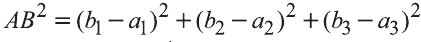
Следовательно,
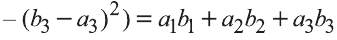
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 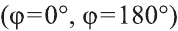
это равенство.
Свойства скалярного произведения векторов
1.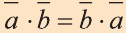
2.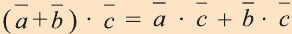
3.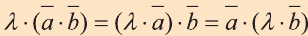
4.Если векторы а и b являются сонаправленными коллинеарными
векторами, то 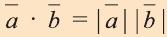
5.Если же векторы противоположно направлены, то 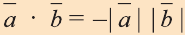
6. 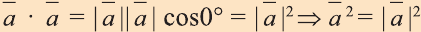
7. Если вектор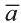

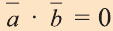
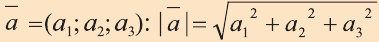
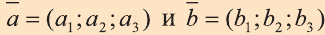
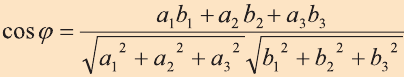
с) условие перпендикулярности векторов 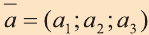
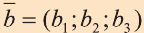
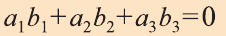
Пример:
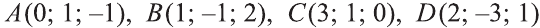
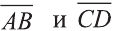
Решение:
Найдём длины векторов 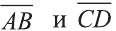
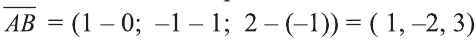
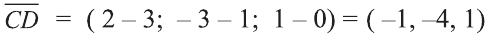
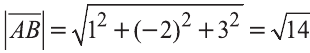
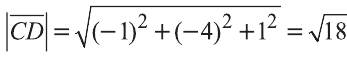
Следовательно,
Пример:
Найдите угол между векторами 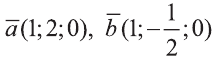
Решение:
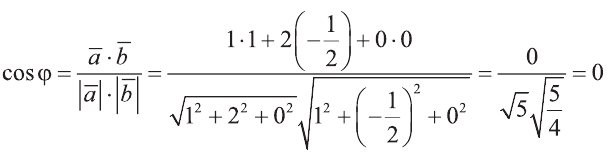
Пример:
Найдите 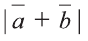
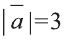
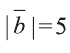


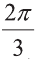
Решение:
Пример:
Найдите координаты и длины векторов 1)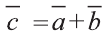
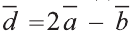
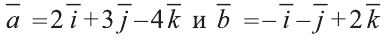
Решение:
Подставим в выражения искомых векторов разложения векторов 

1)
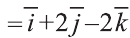
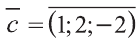
Тогда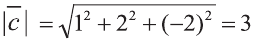
2)
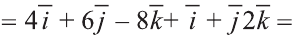
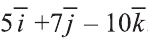
Следовательно, 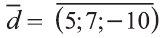
Тогда
- Заказать решение задач по высшей математике
Пример:
Найдите произведение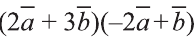


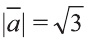
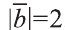
Решение:
Сначала найдём поизведение векторов 

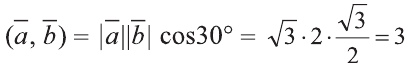
Затем перемножим заданные выражения как многочлены
и, пользуясь распределительным свойством умножения
вектора на число, получим:
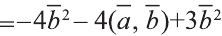
Учитывая, что 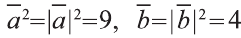
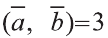
Преобразование и подобие в пространстве
Геометрические преобразования в пространстве
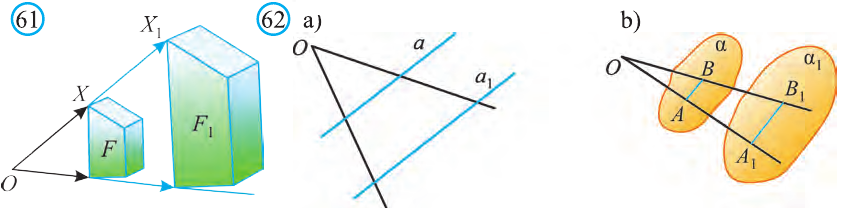
Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.
Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.
Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
Движение и параллельный перенос
Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.
В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.
Простейшим примером движения является параллельный перенос.
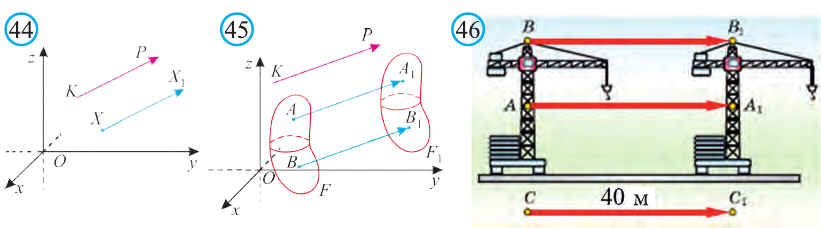
Пусть в пространстве даны вектор
(рис. 44). Говорят, что точка Х перешла в точку X1 параллельным
переносом на вектор 
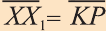

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.
Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,
и т. д.
Пусть точка 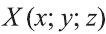
фигуры F1 при помощи параллельного переноса
на вектор 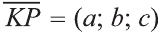
Тогда по определению получим:
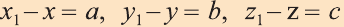
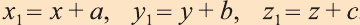
Эти равенства называют формулами параллельного переноса.
Пример:
В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор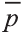
Решение:
По вышеприведённым формулам параллельного переноса: 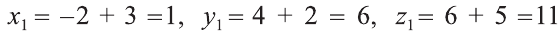
Ответ: 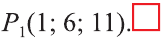
Центральная симметрия в пространстве
Если в пространстве 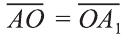
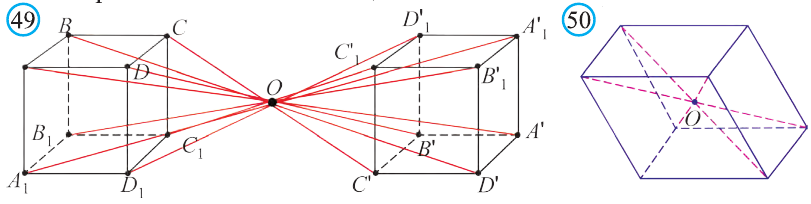
Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.
Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.
Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.
Пример:
В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?
Решение:
Пусть А1 = (х; у; z) — искомая точка. По определению точка
О — середина отрезка АА1. Следовательно,
Из этих уравнений получаем:
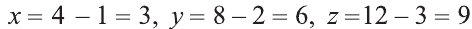
Ответ:
Симметрия относительно плоскости
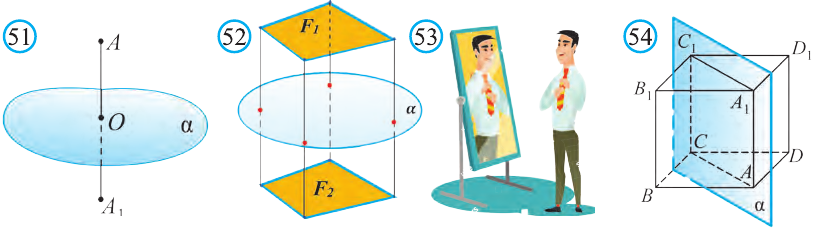
Точки А и А1 называют симметричными относительно плоскости а,
если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F1, и F2 на рисунке 52 симметричны относительно
плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).
Симметрия относительно плоскости а является движением.
Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.
Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.
Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА1 и СС1.
Поворот и симметрия относительно оси
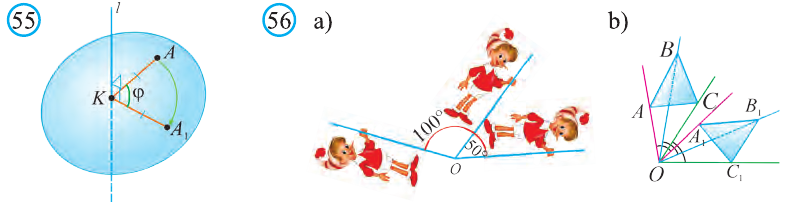
Пусть в пространстве заданы точки А и А1 и прямая l. Если перпендикуляры АК и А1К, опущенные на прямую l, равны и образуют угол 

Если каждую точку фигуры F повернуть на угол 

Поворот относительно прямой также является движением.
Поворот на 180° относительно прямой l называют симметрией относительно прямой l.
Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:
Симметрия в природе и технике
В природе на каждом шагу можно встретить симметрию.
Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.
Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.
Подобие пространственных фигур
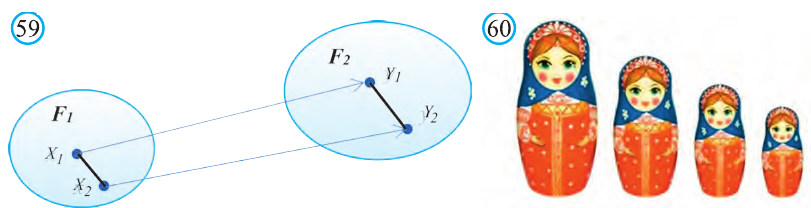
Пусть 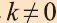
при этом преобразовании для произвольных точек X1 и Х2 фигуры F1 и соответствующих им точек Y1 и Y2 фигуры 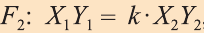
Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.
Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.
Пусть в пространстве задана фигура F, точка О и число к 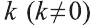
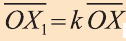


Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
Гомотетия относительно точки О с коэффициентом 




Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней
- Системы неравенств
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
Декартовыми
прямоугольными координатами точки P в
трехмерном пространстве
называются взятые с определенным знаком
расстояния (выраженные в единицах
масштаба) этой точки до трех
взаимно перпендикулярных координатных
плоскостей или, что то же, проекции
радиус-вектора r
точки P на три
взаимно перпендикулярные координатные
оси.
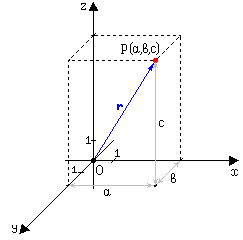
Координаты x, y, z
называются соответственно абсциссой,
ординатой и аппликатой.
Вектор в трехмерном
пространстве определяется тремя
координатами p(x,
y,
z).
Для векторов
трёхмерного пространства указаны
правила сложения векторов и умножения
их на действительные числа
. В применении
к любым векторам х,
у, z и любым
числам a, b
эти правила удовлетворяют следующим
условиям:
-
х +
у =
у +
х
(перестановочность сложения);2)
(х
+
у)
+
z =
x +
(y
+
z)
(ассоциативность сложения);3) имеется
нулевой вектор 0
(или нуль-вектор), удовлетворяющий
условию x +
0 =
x: для любого
вектора x;4)
для любого вектора х
существует противоположный ему вектор
у
такой, что х
+
у =
0,5) 1
· х =
х,6) a(bx)
=
(ab)
х
(ассоциативность умножения);7) (a
+
b)
х =
aх +
bх
(распределительное свойство относительно
числового множителя);a(х
+
у)
=
aх +
aу
(распределительное
свойство относительно векторного
множителя).
14. Уравнение прямой и плоскости в трехмерном пространстве
Всякое
уравнение первой степени относительно
координат x,
y, z
Ax
+ By
+ Cz
+D
= 0
(1)
задает
плоскость, и наоборот: всякая плоскость
может быть представлена уравнением
(1), которое называется уравнением
плоскости.
Вектор
n
(A, B, C ), ортогональный плоскости, называется
нормальным
вектором
плоскости. В уравнении (1) коэффициенты
A, B, C одновременно не равны 0.
Особые
случаи уравнения (3.1):
1.
D = 0, Ax+By+Cz = 0 — плоскость проходит через
начало координат.
2.
C = 0, Ax+By+D = 0 — плоскость параллельна оси
Oz.
3.
C = D = 0, Ax +By = 0 — плоскость проходит через
ось Oz.
4.
B = C = 0, Ax + D = 0 — плоскость параллельна
плоскости Oyz.
Уравнения
координатных плоскостей: x = 0, y = 0, z = 0.
Прямая
в пространстве может быть задана:
1)
как линия пересечения двух плоскостей,т.е.
системой уравнений:
A
1
x
+ B 1
y
+ C 1
z
+ D 1
= 0, A 2
x
+ B 2
y
+ C 2
z
+ D 2
= 0; (2)
2)
двумя своими точками M 1
(x 1,
y 1,
z 1
) и M 2
(x 2,
y 2,
z 2
), тогда прямая, через них проходящая,
задается уравнениями:
=
;
(3)
3)
точкой M 1
(x 1,
y 1,
z 1
), ей принадлежащей, и вектором a
(m, n, р), ей
коллинеарным. Тогда прямая определяется
уравнениями:
.
(4)
Уравнения
(4) называются каноническими
уравнениями прямой.
Вектор
a
называется направляющим
вектором прямой.
Параметрические
уравнения прямой получим,
приравняв каждое из отношений (4) параметру
t:
x
= x
1 +
mt
, y
= y
1 +
nt
, z
= z
1 +
р t
.
(5)
Решая
систему (2) как систему линейных уравнений
относительно неизвестных x
и y,
приходим к уравнениям прямой в проекциях
или к приведенным
уравнениям прямой
:
x
= mz
+ a,
y
= nz
+ b.
(6)
От
уравнений (6) можно перейти к каноническим
уравнениям, находя z
из каждого уравнения и приравнивая
полученные значения:
.
От
общих уравнений (2) можно переходить к
каноническим и другим способом, если
найти какую-либо точку этой прямой и ее
направляющий вектор n
= [ n
1,
n
2
], где n
1
(A 1,
B 1,
C 1
) и n
2
(A 2,
B 2,
C 2
) — нормальные векторы заданных плоскостей.
Если один из знаменателей m,
n или р
в уравнениях (4) окажется равным нулю,
то числитель соответствующей дроби
надо положить равным нулю, т.е. система
равносильна
системе
;
такая прямая перпендикулярна к оси Ох.
Система
равносильна
системе x = x 1,
y = y 1
; прямая параллельна оси Oz.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Трехмерное пространство: векторы, координаты
Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.
Что такое трехмерное пространство
Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.
В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.
Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.
Понятие точки в трехмерном пространстве
Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.
Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.
Разновидности систем координат
Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.
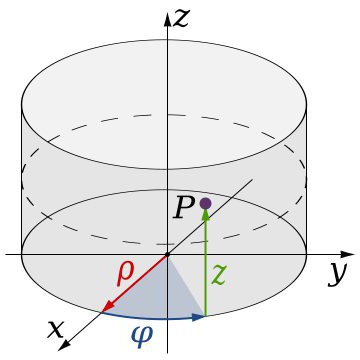
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Понятие прямой в трехмерном пространстве
Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.
Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.
Определение векторов и базиса трехмерного пространства
Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.
Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.
Зависимые и независимые векторы
Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).
Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).
Плоскость в трехмерном пространстве
Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).
К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.
Существует ли более трех измерений
Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.
Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.
Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.
Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.
Заключение
В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).
Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.
Как построить вектор в трехмерном пространстве
Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.
Что такое трехмерное пространство
Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.
В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.
Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.
Понятие точки в трехмерном пространстве
Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.
Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.
Разновидности систем координат
Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Понятие прямой в трехмерном пространстве
Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.
Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.
Определение векторов и базиса трехмерного пространства
Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.
Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.
Зависимые и независимые векторы
Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).
Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).
Плоскость в трехмерном пространстве
Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).
К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.
Существует ли более трех измерений
Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.
Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.
Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.
Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.
Заключение
В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).
Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.
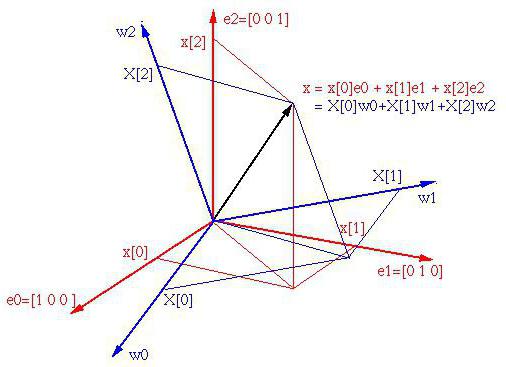
Геометрическим представлением вектора является направленный отрезок прямой линии, что показано на рис. 1. У каждого вектора есть два свойства: длина (также называемая модулем или нормой вектора) и направление . Благодаря этому векторы очень удобны для моделирования физических величин, которые характеризуются модулем и направлением. Например, в главе 14 мы реализуем систему частиц. При этом мы будем использовать векторы для моделирования скорости и ускорения наших частиц. С другой стороны, в трехмерной компьютерной графике векторы часто используются только для моделирования направления. Например, нам часто требуется указать направление распространения световых лучей, ориентацию грани или направление камеры, глядящей на трехмерный мир. Векторы обеспечивают удобный механизм задания направления в трехмерном пространстве.
Рис. 1. Свободные векторы, определенные независимо от системы координат
Поскольку местоположение не является характеристикой вектора, два вектора с одинаковой длиной и указывающие в одном и том же направлении считаются равными, даже если они расположены в различных местах. Обратите внимание, что два таких вектора будут параллельны друг другу. Например, на рис. 1 векторы u и v равны.
На рис. 1 видно, что обсуждние векторов может вестись без упоминания системы координат, поскольку всю значимую информацию, — длину и направление, — вектор содержит в себе. Добавление системы координат не добавляет информации в вектор; скорее можно говорить, что вектор, значения которого являются его неотъемлимой частью, просто описан относительно конкретной системы координат. И если мы изменим систему координат, мы только опишем тот же самый вектор относительно другой системы.
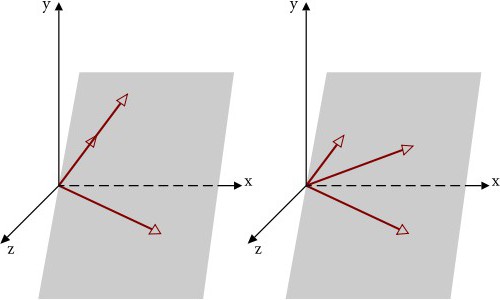
Отметив этот важный момент, мы перейдем к изучению того, как векторы описываются в левосторонней трехмерной декартовой системе координат. На рис. 2 показаны левосторонняя и правосторонняя системы координат. Различие между ними — положительное направление оси Z. В левосторонней системе координат положительное направление оси Z погружается в страницу. В правосторонней системе координат положительное направление оси Z направлено от страницы.
Рис. 2. Слева изображена левосторонняя система координат. Обратите внимание, что положительное направление оси Z направлено вглубь страницы. Справа изображена правостороняя система координат. Здесь положительное направление оси Z направлено от страницы
Поскольку местоположение вектора не изменяет его свойств, мы можем перенести векторы таким образом, чтобы начало каждого из них совпадало с началом координат выбранной координатной системы. Когда начало вектора совпадает с началом координат, говорят, что вектор находится в стандартной позиции . Таким образом, если вектор находится в стандартной позиции, мы можем описать его, указав только координаты конечной точки. Мы будем называть эти координаты компонентами вектора. На рис. 3 показаны векторы, изображенные на рис. 1, которые были перемещены в стандартные позиции.
Рис. 3. Векторы в стандартной позиции, определенные в указанной системе координат. Обратите внимание, что векторы u и v полностью совпадают друг с другом потому что они равны
Поскольку мы описываем находящийся в стандартной позиции вектор, указывая его конечную точку, как если бы мы описывали отдельную точку, легко перепутать точку и вектор. Чтобы подчеркнуть различия между этими двумя понятиями, мы вновь приведем определение каждого из них. Точка описывает только местоположение в системе координат, в то время как вектор описывает величину и направление.
Мы будем пользоваться для обозначения векторов полужирными строчными буквами, но иногда будем применять и полужирные заглавные буквы. Вот пример двух-, трех- и четырехмерных векторов соответственно: u = ( u x , u y ), N = ( N x , N y , N z ), c = ( c x , c y , c z , c w ).
Теперь мы введем четыре специальных трехмерных вектора, которые показаны на рис. 4. Первый из них называется нулевым вектором , и значения всех его компонент равны нулю; мы будем обозначать такой вектор выделенным полужирным шрифтом нулем: 0 = (0, 0, 0). Следующие три специальных вектора называются единичными базовыми векторами (базовыми ортами) трехмерной системы координат. Эти векторы, направленные вдоль осей X, Y и Z нашей координатной системы, мы будем называть i , j и k соответственно. Модуль этих векторов равен единице, а определение выглядит следующим образом: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
Рис. 4. Нулевой вектор и базовые орты трехмерной системы координат
Вектор, длина которого равна единице, называется единичным вектором или ортом .
В библиотеке D3DX для представления векторов в трехмерном пространстве мы можем воспользоваться классом D3DXVECTOR3 . Его определение выглядит следующим образом:
Обратите внимание, что D3DXVECTOR3 наследует компоненты от D3DVECTOR , определение которого выглядит следующим образом:
Так же, как и у скалярных величин, у векторов есть собственная арифметика, что видно из наличия описаний математических операций в определении класса D3DXVECTOR3. Возможно, сейчас вы не знаете, что делают эти методы. В следующих подразделах мы рассмотрим эти операции с векторами, другие вспомогательные функции работы с векторами из библиотеки D3DX и некоторые важные особенности обработки векторов.
Хотя основной интерес для нас представляют векторы в трехмерном пространстве, занимаясь программированием трехмерной графики мы будем иногда сталкиваться с векторами в двухмерном и четырехмерном пространствах. Библиотека D3DX предоставляет классы D3DXVECTOR2 и D3DXVECTOR4 , предназначенные для представления векторов в двухмерном и четырехмерном пространствах соответственно. Векторы в пространствах с другим количеством измерений обладают теми же свойствами, что и векторы в трехмерном пространстве, а именно — длиной и направлением, отличается только количество измерений. Кроме того, математические операции с векторами, за исключением векторного произведения (см. раздел «Векторное произведение», далее в этой главе), которое определено только для трехмерной системы координат, могут быть обобщены для векторов любой размерности. Таким образом, за исключением векторного произведения, все операции, которые мы обсуждаем для векторов в трехмерном пространстве, распространяются и на векторы в двухмерном, четырехмерном и даже n-мерном пространствах.
Равенство векторов
В геометрии два вектора считаются равными, если они указывают в одном и том же направлении и имеют одинаковую длину. В алгебре говорят, что векторы равны, если у них одинаковое количество измерений и их соответствующие компоненты равны. Например, ( u x , u y , u z ) = ( v x , v y , v z ) если u x = v x , u y = v y и u z = v z .
В коде мы можем проверить равны ли два вектора, используя перегруженный оператор равенства:
Аналогичным образом, можно убедиться, что два вектора не равны, используя перегруженный оператор неравенства:
Сравнивая числа с плавающей точкой следует быть очень аккуратным, поскольку из-за погрешностей округления, два числа с плавающей точкой, которые должны быть равными, могут слегка отличаться. По этой причине мы проверяем приблизительное равенство чисел с плавающей точкой. Для этого мы определили константу EPSILON , содержащую очень маленькое значение, которое будет служить «буфером». Мы будем говорить, что два числа приблизительно равны, если разница между ними меньше EPSILON . Другими словами, EPSILON дает нам некий допуск для ошибок округления чисел с плавающей точкой. Приведенная ниже функция показывает, как EPSILON может использоваться при проверке равенства двух чисел с плавающей точкой: Об этом не надо беспокоиться, работая с классом D3DXVECTOR , поскольку перегруженные операции сравнения все сделают за нас, но очень важно знать об этой особенности сравнения чисел с плавающей точкой.
Вычисление модуля вектора
В геометрии модулем вектора называется длина направленного отрезка линии. В алгебре, зная компоненты вектора мы можем вычислить его модуль по следующей формуле:
Вертикальные линии в |u| обозначают модуль u .
Вычислите модуль векторов u = (1, 2, 3) и v = (1, 1).
Решение
Для вектора u мы получаем:
Обобщив формулу (1) для двухмерного пространства, для вектора v мы получим:
Работая с библиотекой D3DX, для вычисления модуля вектора мы можем применять следующую функцию:
Нормализация вектора
В результате нормализации получается вектор, направление которого совпадает с исходным, а модуль равен единице (единичный вектор). Чтобы нормализовать произвольный вектор, достаточно разделить каждый компонент вектора на модуль вектора, как показано ниже:
Мы отмечаем единичный вектор, помещая над его обозначением символ ^ : û .
Нормализуйте векторы u = (1, 2, 3) и v = (1, 1).
Решение
Из приведенных выше формул (2) и (3) мы знаем, что |u| = √ 14 и |v| = √ 2 , поэтому:
В библиотеке D3DX для нормализации векторов применяется следующая функция:
Эта функция возвращает указатель на результат, который может быть передан в качестве параметра другой функции. В большинстве случаев, за исключением явно указанных, математические функции библиотеки D3DX возвращают указатель на результат. Мы не будем явно говорить это для каждой функции.
Сложение векторов
Мы можем сложить два вектора, сложив их соответствующие компоненты; обратите внимание, что размерность складываемых векторов должна быть одинаковой:
Геометрическая интерпретация сложения векторов показана на рис. 5.
Рис. 5. Сложение векторов. Обратите внимание, как мы выполняем параллельный перенос вектора v таким образом, чтобы его начало совпало с концом вектора u ; суммой будет вектор начало которого совпадает с началом вектора u , а конец совпадает с концом перенесенного вектора v
В коде для сложения двух векторов мы будем применять перегруженый оператор сложения:
Вычитание векторов
Аналогично сложению, вычитание векторов осуществляется путем вычитания их отдельных компонент. Опять же оба вектора должны иметь одинаковую размерность.
Геометрическая интерпретация вычитания векторов показана на рис. 6.
Рис. 6. Вычитание векторов
В коде для вычитания двух векторов мы будем применять перегруженый оператор вычитания:
Как видно на рис. 6, операция вычитания векторов возвращает вектор, начало которого совпадает с концом вектора v , а конец — с концом вектора u . Если мы интерпретируем компоненты u и v как координаты точек, то результатом вычитания будет вектор, направленный от одной точки к другой. Это очень удобная операция, поскольку нам часто будет необходимо найти вектор, описывающий направление от одной точки к другой.
Умножение вектора на скаляр
Как видно из названия раздела, мы можем умножать вектор на скаляр, в результате чего происходит масштабирование вектора. Если масштабный множитель положителен, направление вектора не меняется. Если же множитель отрицателен, то направление вектора изменяется на противоположное (инвертируется).
Класс D3DXVECTOR3 предоставляет оператор умножения вектора на скаляр:
Скалярное произведение векторов
Скалярное произведение векторов — это первая из двух определенных в векторной алгебре операций умножения. Вычисляется такое произведение следующим образом:
У приведенной выше формулы нет очевидной геометрической интерпретации. Используя теорему косинусов 1 , мы получим отношение u Ч v = |u||v| cos j , говорящее, что скалярное произведение двух векторов равно произведению косинуса угла между векторами на модули векторов. Следовательно, если u и v — единичные векторы, их скалярное произведение равно косинусу угла между ними.
Вот некоторые полезные свойства скалярного произведения:
- Если u Ч v = 0, значит u ^ v .
- Если u Ч v > 0, значит угол j между двумя векторами меньше 90 градусов.
- Если u Ч v j между двумя векторами больше 90 градусов.
Символ ^ обозначает «ортогональный» или (что то же самое) «перпендикулярный».
Для вычисления скалярного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
Векторное произведение
Второй формой операции умножения, определенной в векторной алгебре, является векторное произведение. В отличие от скалярного произведения, результатом которого является число, результатом векторного произведения будет вектор. Векторным произведением двух векторов u и v будет другой вектор, p , являющийся взаимно перпендикулярным для векторов u и v . Это означает, что вектор p перпендикулярен вектору u и одновременно вектор p перпендикулярен вектору v .
Вычисляется векторное произведение по следующей формуле:
В компонентной форме вычисление выглядит так:
Рис. 7. Векторное произведение. Вектор p = u × v перпендикулярен как вектору u, так и вектору v
Вычислите j = k × i = (0, 0, 1) × (1, 0, 0) и проверьте, что вектор j перпендикулярен как вектору i , так и вектору k .
Решение
Таким образом, j = (0, 1, 0). Вспомните, в предыдущем разделе «Скалярное произведение векторов» говорилось, что если u Ч v = 0, значит u ^ v . Поскольку j Ч k = 0 и j Ч i = 0, мы знаем что вектор j перпендикулярен как вектору k , так и вектору i .
Для вычисления векторного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
Как явствует из рис. 7, вектор –p также взаимно перпендикулярен векторам u и v . Какой из векторов, p или –p будет возвращен в качестве результата векторного произведения определяется порядком операндов. Другими словами, u × v = –( v × u ). Это заначит, что операция векторного произведения не является коммутативной. Определить, какой вектор будет возвращен в качестве результата, можно с помощью правила левой руки . (Мы используем правило левой руки, поскольку работаем с левосторонней системой координат. Если бы у нас была правосторонняя система координат, пришлось бы воспользоваться правилом правой руки.) Если расположить пальцы левой руки вдоль первого вектора, а ладонь руки — вдоль второго, отогнутый на 90 градусов большой палец укажет направление результирующего вектора.
1 Теорема косинусов определяет зависимость между сторонами и углами треугольника. Она утверждает, что во всяком треугольнике квадрат длины стороны равен сумме квадратов двух других сторон без удвоенного произведения длин этих сторон на косинус угла между ними. Если угол прямой, то теорема косинусов переходит в теорему Пифагора, т.к. косинус прямого угла равен 0.
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
http://www.syl.ru/article/225252/new_trehmernoe-prostranstvo-vektoryi-koordinatyi
http://hd01.ru/info/kak-postroit-vektor-v-trehmernom-prostranstve/
Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.
Оси координат (Ox), (Oy) и (Oz) называются соответственно: (Ox) — ось абсцисс, (Oy) — ось ординат, (Oz) — ось аппликат.
Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: ((Oxy)), ((Oyz)) и ((Oxz)).
Положение точки (A) в пространстве определяется тремя координатами: (x), (y) и (z).
Координата (x) называется абсциссой точки (A), координата (y) — ординатой точки (A), координата (z) — аппликатой точки (A).
Записываются так: (A(x; y; z)).
Если точка находится на оси (Ox), то её координаты (X(x; 0; 0)).
Если точка находится на оси (Oy), то её координаты (Y(0; y; 0)).
Если точка находится на оси (Oz), то её координаты (Z(0; 0; z)).
Если точка находится в плоскости (Oxy), то её координаты
A1x;y;0
.
Если точка находится в плоскости (Oyz), то её координаты
A20;y;z
.
Если точка находится в плоскости (Oxz), то её координаты
A3x;0;z
.
Если в системе координат от начальной точки отложить единичные векторы
i→
,
j→
и
k→
, то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде
OA→=x⋅i→+y⋅j→+z⋅k→
.
Коэффициенты (x), (y) и (z) определяются одним-единственным образом и называются координатами вектора.
Записываются так:
OA→x;y;z
.
Рассмотрим правила о том, как с помощью координат записать:
— координаты суммы векторов, если даны координаты векторов:
,
b→x2;y2;z2
,
a→+b→x1+x2;y1+y2;z1+z2
;
— координаты разности векторов, если даны координаты векторов:
a→−b→x1−x2;y1−y2;z1−z2
;
— координаты произведения вектора на число, если даны координаты вектора:
— длину вектора:
— координаты вектора, если даны координаты начальной и конечной точек вектора:
,
BxB;yB;zB
,
AB→xB−xA;yB−yA;zB−zA
;
— расстояние между двумя точками, если даны координаты точек:
;
— координаты серединной точки отрезка, если даны координаты начальной и конечной точек отрезка:
.
Векторы и координаты в пространстве. Геометрический подход
Мы с вами уже знаем про такие математические инструменты, как векторы и координаты; подробно говорили о том, почему в них возникает необходимость и где мы их используем. Кто не помнит – пересмотрите урок по геометрии-9.
В планиметрии мы рассматривали векторные величины на плоскости (или, по-другому, в двумерном пространстве). Для того чтобы задать вектор, нам было достаточно двух координат. В стереометрии мы решаем задаче в привычном нам трехмерном пространстве, и теперь двух координат для задания вектора нам будет недостаточно.
Действительно, представьте себе лягушку, которая собирается поймать комара. Если она будет знать только то, что он в 3 см впереди и на 2 см правее ее, то шансы на удачную охоту будут невысокими. Другой пример: два самолета могут одновременно лететь 30 км южнее и 40 км восточнее Москвы, если будут находиться на разной высоте (на разных эшелонах).
Чтобы задать вектор в трехмерном пространстве, нам понадобятся три координаты. Повлияет ли это на уже полученные нами свойства векторов? Мы расширяем математические инструменты таким образом, чтобы все уже известные нам свойства и характеристики сохранялись. Такая же ситуация и с векторами и координатами в пространстве – принципиально нового будет немного.
В планиметрии мы параллельно рассматривали два подхода к описанию вектора:
- Геометрический: вектор – направленный отрезок.
- Алгебраический: вектор – это упорядоченная пара чисел – координат вектора.
Используем их для определения вектора в пространстве.
C геометрической точки зрения вектором называется направленный отрезок, т. е. отрезок в пространстве, для которого указаны начало и конец (см. рис. 1).
Рис. 1. Вектор
Обозначается вектор двумя большими или одной малой буквами со стрелкой или черточкой наверху: . Направление вектора считается от начала вектора к концу. Длина отрезка называется длиной или модулем вектора:
. Отдельную точку пространства можно считать вектором нулевой длины. Направление такого вектора не определено. Обозначается он как ноль со стрелочкой:
.
Векторы могут образовывать разные углы, но есть особые случаи: векторы, которые действуют строго в одном направлении или в прямо противоположных. Например, во втором законе Ньютона результирующая внешних сил и ускорение – векторы, направленные в одну сторону, а в третьем законе Ньютона силы направлены в противоположных направлениях. Формальные понятия сонаправленности и противоположной направленности, а также их общего случая – коллинеарности в пространстве остаются без изменений.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Проще говоря, параллельные векторы мы называем коллинеарными.
Рис. 2. Коллинеарные векторы
Два коллинеарных вектора, направленные в одну сторону, называются сонаправленными:
Если они направлены в разные стороны, то их называют противоположно направленными (см. рис. 3):
Рис. 3. Противоположно направленные векторы
Нулевой вектор считается сонаправленным с любым другим вектором. Для обозначения коллинеарности, сонаправленности и противоположно направленности мы используем знак параллельности, сонаправленные или противоположные стрелки.
В параллелепипеде (см. рис. 4):
и
не являются коллинеарными.
Рис. 4. Рассматриваемый параллелепипед
Равными векторами, как и прежде, будем называть сонаправленные векторы равной длины. Т. к. векторы и
сонаправлены и имеют равную длину, то:
и
не являются коллинеарными, следовательно:
и
сонаправлены, но имеют разную длину, следовательно:
и
имеют равную длину, но противоположно направлены, следовательно:
Векторы и координаты в пространстве. Алгебраический подход
Рассмотрим теперь алгебраический подход к определению вектора. Для этого расширим понятие декартовой системы координат с плоской до пространственной.
Проведем три взаимно перпендикулярные прямые через одну точку. Выберем направление на каждой прямой и назовем их координатными осями. Общую точку назовем началом координат и обозначим буквой . Выберем масштаб, для этого на каждой оси отметим единицу (см. рис. 5).
Рис. 5. Пространственная система координат
Стандартное обозначение для осей . Стандартное расположение осей –
и
в горизонтальной плоскости,
направлена в нашу сторону,
– вправо. Ось
направлена вертикально вверх. Как и раньше, ось
называется осью абсцисс, а
– осью ординат. Ось
называется осью аппликат.
Чтобы выяснить координаты произвольной точки, необходимо, как и в плоском случае, опустить перпендикуляры из точки на каждую координатную ось.
При изображении важным является то обстоятельство, что если изобразить оси и точку, то еще непонятно, где она находится. Кажется, что точки и
находятся в одном и том же месте (см. рис. 6). На самом деле, мы этого еще не знаем. Для определения позиции точек обычно строят их проекции на плоскость
.
Рис. 6. Расположение точек и
У точек и их проекций координаты и
совпадают. Чтобы найти координату
, проекцию точки соединяют с началом координат, а потом из точки проводят параллельный отрезок до пересечения с осью аппликат. Полученные координаты называются, соответственно, абсциссой, ординатой и аппликатой точки (см. рис. 7). Записываются координаты точки в виде упорядоченной тройки чисел: абсцисса, ордината, аппликата.
Рис. 7. Полученные координаты точек и
Теперь перейдем к векторам и их координатам. Вспомним, как на плоскости мы задавали координаты вектора. Если на векторе как на гипотенузе построить прямоугольный треугольник с катетами, параллельными осям, то длины катетов и принимаются за координаты вектора. При таком определении равные векторы получают равные координаты. Координаты вектора с началом в точке совпадают с координатами конца вектора (см. рис. 8).
Рис. 8. Векторы
При этом если вектор смотрит влево, т. е. его проекция на ось отрицательна, то координата
вектора считается отрицательной. Аналогично для координаты
. Если вектор смотрит вниз, то его координата у отрицательна.
Вектор смотрит вправо и вниз – у него положительная координата
и отрицательная
.
Вектор смотрит влево и вверх, координата
отрицательная,
положительная.
Вектор смотрит влево и вниз, обе координаты отрицательны (см. рис. 9).
Рис. 9. Векторы
Чтобы найти координаты, очевидно, нужно из координат конца вектора вычесть координаты начала. Длину вектора можно было выразить, используя теорему Пифагора:
Используем описанный для плоскости подход в пространстве. А именно – у равных векторов должны быть равные координаты (чтобы геометрический и алгебраический подход описывал один и тот же инструмент).
На векторе, как на диагонали, строим прямоугольный параллелепипед с ребрами, параллельными координатным осям.
Рис. 10. Построенный параллелепипед
Очевидно, на равных векторах будут построены равные параллелепипеды (см. рис. 11).
Рис. 11. На равных векторах построены равные параллелепипеды
Три измерения параллелепипеда назовем координатами вектора. У равных двух векторов на рисунке выше равны координаты: . Вычислить их можно как разности соответствующих координат конца и начала вектора:
При этом учитывается направление. Если вектор смотрит в отрицательную сторону вдоль какой-то из осей, то координата отрицательна.
Т. к. длина вектора – это длина диагонали параллелепипеда, то ее можно вычислить по теореме Пифагора:
Пример 1. Найти координаты и длину вектора с началом в точке и концом в точке
(см. рис. 12).
Рис. 12. Иллюстрация к примеру 1
Решение
Найдем координаты вектора. Для этого вычтем из координат конца координаты начала:
Отрицательные первая и третья координаты означают тот факт, что вдоль осей и
вектор смотрит в отрицательном направлении.
Вычислим его длину:
Ответ: ;
.
С алгебраической точки зрения вектором называется любая упорядоченная тройка чисел. Равные тройки называются равными векторами. Небольшое противоречие состоит в том, что с геометрической точки зрения два несовпадающих, но равных направленных отрезка – это два вектора, равных друг другу. А с алгебраической, т. к. они имеют одинаковый набор координат – это просто один вектор.
Разрешается это противоречие следующим образом. Все равные геометрические векторы считают одним вектором, а конкретные направленные отрезки – различными представлениями этого вектора. Так что в дальнейшем для нас не будет особой разницы сказать «векторы равны» или «это один и тот же вектор».
Рассмотрим коллинеарность векторов с алгебраической точки зрения. Мы знаем, что на плоскости коллинеарность векторов означает пропорциональность их координат. В самом деле, два коллинеарных вектора можно заменить на равные им радиус-векторы. Они будут лежать на одной прямой. Из подобия прямоугольных треугольников следует пропорциональность их координат (см. рис. 13). Во сколько раз длиннее вектор, во столько раз больше модули его координат.
Рис. 13. Коллинеарные векторы
Векторы и
коллинеарны, и их координаты пропорциональны:
Абсолютно аналогичная ситуация в трехмерном случае. Пусть и
– коллинеарные векторы. Соответствующие им радиус-векторы лежат на одной прямой. Тогда из подобия двух параллелепипедов следует пропорциональность их координат (см. рис. 14). Таким образом, чтобы выяснить коллинеарность двух векторов, нужно попарно поделить их координаты друг на друга.
Рис. 14. Коллинеарные векторы
Пример 2. Выяснить, коллинеарны ли пары векторов:
1. и
;
2. и
;
3. и
.
Решение
1. и
:
Координаты пропорциональны, значит, векторы коллинеарны. Отношение координат – положительное число . Значит, вектор
в
раза длиннее и сонаправлен вектору
.
2. и
:
Координаты пропорциональны, значит, векторы коллинеарны. Отношение – отрицательное число . Значит, вектор
в
раза длиннее и противоположно направлен вектору
.
3. и
:
Координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: да, да, нет.
Сложение и вычитание векторов. Умножение вектора на число
Рассмотрим два произвольных вектора в пространстве. Совместим конец вектора и начало вектора
(см. рис. 15).
Рис. 15. Конец вектора совместили с началом вектора
Если у двух векторов есть общая точка, то они лежат в одной плоскости. Тогда, чтобы расширенная модель не противоречила исходной, для сложения векторов нужно использовать правило треугольника.
Суммой будет вектор , начало которого совпадает с началом вектора
, а конец – с концом вектора
(см. рис. 16):
Рис. 16. Вектор
Иллюстрирует это правило нагляднее всего перемещение: переместиться из точки на вектор
в точку
, а затем из точки
на вектор
в точку
эквивалентно перемещению из точки
в точку
(см. рис. 17).
Рис. 17. Иллюстрация правила сложения векторов
Точно так же сохраняется и правило параллелограмма. Если совместить два вектора, и
не последовательно, а так, чтобы совпали их начала, то одна диагональ
построенного на них параллелограмма будет суммой, а вторая диагональ
– разностью данных векторов (см. рис. 18):
Рис. 18. Векторы и
Проверяем себя, куда направить векторы разности, как и раньше:
Два вектора называются противоположными, если они в сумме дают нулевой вектор.
Понятно, что это должны быть противоположно направленные равные по модулю векторы:
Как и в плоском случае, последовательное применение несколько раз правила треугольника для сложения нескольких векторов дает правило многоугольника. Единственная разница будет в том, что многоугольник уже может не быть плоским.
Чтобы сложить несколько векторов, нужно совместить последовательно их концы и начала, и результатом будет вектор, начало которого совпадает с началом первого, а конец – с концом второго:
Например, чтобы сложить векторы (см. рис. 19), рассмотрим сумму:
Рис. 19. Векторы
С алгебраической точки зрения тоже никаких изменений с определением сложения не произошло. Складывая два вектора и
в декартовой системе координат, расположим начало вектора
в начале координат, с его концом совместим начало вектора
. По правилу треугольника построим их сумму (см. рис. 20).
Рис. 20. Вектор
Очевидно, как и в плоском случае, координаты суммы – это сумма координат исходных векторов:
Как обратную операцию получаем разность векторов. Чтобы найти разность векторов, нужно из координат первого вектора вычесть координаты второго вектора:
Противоположным данному называется вектор с противоположными координатами:
Умножение вектора на число также не претерпевает изменений по сравнению с плоским случаем. С геометрической точки зрения умножить вектор на положительное число означает изменить его длину в это количество раз, а направление оставить прежним, например (см. рис. 21):
Рис. 21. Векторы и
Если умножить на отрицательное число, то длина вектора меняется пропорционально модулю множителя, а направление меняется на противоположное, например (см. рис. 22):
Рис. 21. Векторы и
Т. е. умножение на число, по модулю большее единицы, удлиняет вектор, а на число, по модулю меньшее единицы, укорачивает.
Важно понимать, что результатом умножения вектора на число всегда является вектор, поэтому при умножении вектора на ноль получаем нулевой вектор, а не число ноль.
Понятно, что, если умножить вектор на , получим вектор той же длины, но направленный в другую сторону – это соответствует нашему определению противоположного вектора:
Рассмотрим теперь вектор в декартовой системе координат. Построенный на нем как на диагонали прямоугольный параллелепипед задает координаты вектора. Умножим вектор на число
в геометрическом смысле, т. е. удлиним его в
раз. Новый параллелепипед будет подобен прежнему с коэффициентом подобия
(см. рис. 22). Значит, его измерения будут отличаться в
раз от исходных. Но его измерения и есть координаты нового вектора. Следовательно, изменение длины вектора в
раз означает умножение его координат на
. Изменение направления вектора означает изменение знака его координат на противоложный.
Рис. 22. Параллелепипеды подобны с коэффициентом
Таким образом, чтобы умножить вектор на число, надо умножить все его координаты на это число:
Абсолютно без изменения остаются основные свойства умножения вектора на число – сочетательный и два распределительных закона. Сочетательный закон утверждает, что можно перемножить два числа, а потом умножить результат на вектор либо поочередно умножать вектор на эти числа. Результат будет одинаков:
Распределительные законы утверждают, что можно раскрывать скобки при умножении суммы чисел на вектор и умножении числа на сумму векторов:
Убедиться в истинности этих законов не составит никакого труда, если использовать координатную форму записи векторов. Попробуйте сделать это самостоятельно.
Компланарные векторы
Пока ничего нового по сравнению с плоским случаем мы про векторы не рассказали.
Но вот следующее понятие имеет смысл только в трехмерном случае. Если несколько векторов имеют общее начало, то они могут лежать в одной плоскости или нет.
Если они лежат в одной плоскости, то их называют компланарными.
Векторы компланарны (см. рис. 23).
Рис. 23. Компланарные векторы
Мы не различаем равные векторы, поэтому в этом примере вектор можем заменить на равный ему вектор
. Таким образом, векторы
компланарны. Иными словами, векторы компланарны, если они все параллельны одной плоскости, в данном случае плоскости нижнего основания.
Векторы некомпланарны (см. рис. 24).
Рис. 24. Некомпланарные векторы
Понятно, что два вектора всегда компланарны. Разберемся, каковы условия компланарности векторов. Вспомним из курса планиметрии еще одно понятие – разложение вектора. Если верно равенство , то говорят, что вектор
разложен по векторам
и
.
Но из курса планиметрии мы также знаем, что такой вектор будет лежать в одной плоскости с векторами
и
. В самом деле, векторы
лежат в плоскости одного и того же параллелограмма, как следует из правил умножения векторов на число и сложения векторов. Таким образом, если один из трех векторов раскладывается по двум другим, то такие три вектора компланарны.
Верно и обратное. Если три вектора компланарны, то любой из них можно разложить по двум оставшимся при условии, что эти два вектора не коллинеарны. Это легко доказать, перейдя в плоскость, в которой лежит эта тройка векторов, и воспользоваться соответствующим утверждением из планиметрии, а именно, что любой вектор можно разложить по двум неколлинеарным векторам.
Что касается алгебраического представления векторов, то здесь проверка компланарности трех векторов сводится к решению соответствующего уравнения c переменными и
.
Пример 3. Проверить, являются векторы компланарными.
Решение
Запишем уравнение:
Умножим в правой части векторы на числа и сложим их:
Два вектора равны, если попарно равны все их координаты. Получаем систему трех простых уравнений:
Ее решение:
Таким образом:
Ответ: векторы компланарны.
Рассмотрим три некомпланарных вектора и найдем их сумму. В алгебраическом подходе нет никакой разницы, складывать ли компланарные или некомпланарные векторы – нужно сложить все соответствующие координаты.
Для геометрического подхода можно сформулировать простое правило параллелепипеда.
Совместим три вектора в общее начало. Построим на них, как на ребрах, параллелепипед (см. рис. 25).
Рис. 25. Построенный параллелепипед
Сложим сначала векторы и
:
Теперь сложим и вектор
:
Таким образом, сумма трех некомпланарных векторов равна диагонали параллелепипеда, построенного на этих векторах.
Теорема о разложении вектора по трем некомпланарным
Мы уже знаем, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам. Аналогичное утверждение сформулируем для векторов в пространстве.
Теорема. Любой вектор в трехмерном пространстве можно разложить единственным образом по любым трем некомпланарным векторам.
Понятно, почему речь идет о некомпланарных векторах. Если мы возьмем компланарные векторы, будем их умножать на разные и числа и складывать друг с другом, мы не выйдем за пределы плоскости, в которой они лежат. Итак, докажем утверждение.
Доказательство
Пусть – данные некомпланарные векторы (см. рис. 26).
Рис. 26. Иллюстрация к доказательству
Докажем для начала, что любой вектор можно разложить по этим трем векторам, а потом докажем единственность такого разложения.
Совместим все четыре вектора в общее начало . Обозначим концы векторов такими же буквами, как векторы, только заглавными (см. рис. 27).
Рис. 27. Иллюстрация к доказательству
Через точку проведем прямую, параллельную вектору
. Она пересечет плоскость
в некоторой точке
. Через
проведем прямую, параллельную
. Она пересечет прямую
в некой точке
(см. рис. 28).
Рис. 28. Иллюстрация к доказательству
Легко увидеть, что:
Но каждый из векторов в правой части равенства коллинеарен одному из исходных трех векторов, т. е. получается из них умножением на некое число. Тогда:
Таким образом, мы разложили вектор по векторам
.
Докажем единственность такого разложения. Предположим, что существует два разложения вектора :
Вычтем из первого второе уравнение:
Т. к. ни один из векторов не является нулевым (ответьте, почему), то это означает, что все разности в скобках равны нулю. В самом деле, если, например,
, то:
Но это означает, что векторы компланарны, что противоречит условию. А раз все разности в скобках равны нулю, то рассматриваемые разложения совпадают – получили противоречие. Значит, такое разложение будет единственным.
Доказано.
Рассмотрим три единичных вектора, т. е. три вектора с длиной , направленных вдоль осей координат. Стандартное обозначение для них
(см. рис. 29). Т. к. эти векторы некомпланарны, то по ним можно разложить любой другой вектор.
Рис. 29. Векторы
Разложим вектор по этим трем векторам (см. рис. 30).
Рис. 30. Вектор
Для этого умножим вектор на число
. Очевидно, получим вектор
. Аналогично умножим вектор
на
, а вектор
– на
. Сумма полученных векторов по правилу параллелепипеда равна вектору
(см. рис. 31).
Рис. 31. Построенный параллелепипед
Т. е., чтобы разложить вектор по этим трем, нужно в качестве коэффициентов использовать его координаты:
В связи с этим векторы называют координатными.
Правило разложения по координатным векторам можно увидеть и из других соображений.
Выпишем координаты самих координатных векторов:
Тогда, очевидно, разложение вектора имеет вид:
Таким образом, координаты вектора и коэффициенты при его разложении по координатным векторам – это одно и то же. Впрочем, мы уже сталкивались с идентичной ситуацией в планиметрии. Только координатных векторов было всего два.
Список литературы
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
- Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал mathprofi.ru
- Интернет-портал ru.onlinemschool.com
Домашнее задание
- Найти координаты и длину вектора
, если
и
.
- Даны векторы
и
. Найти координаты вектора
.
– тетраэдр,
– середины его ребер
. Компланарны ли векторы
?