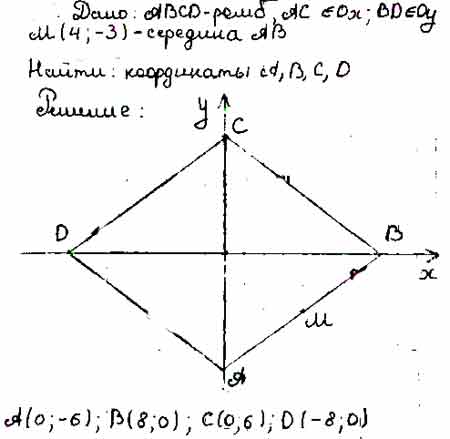
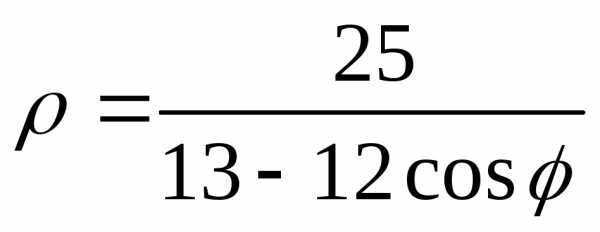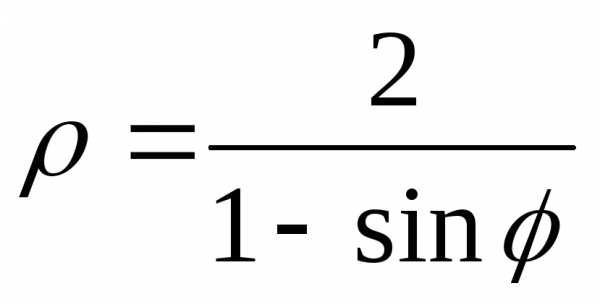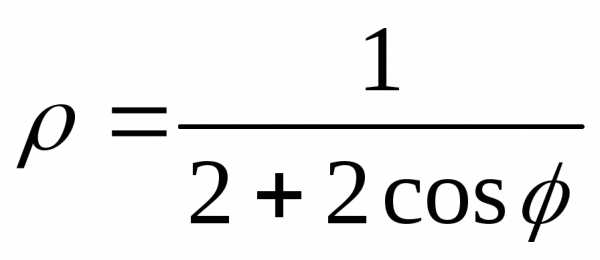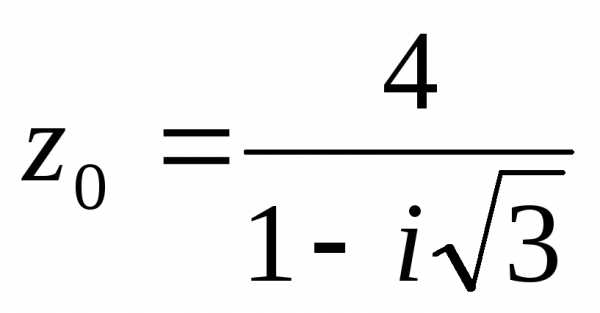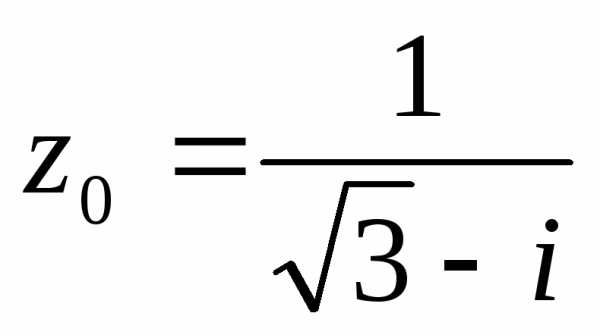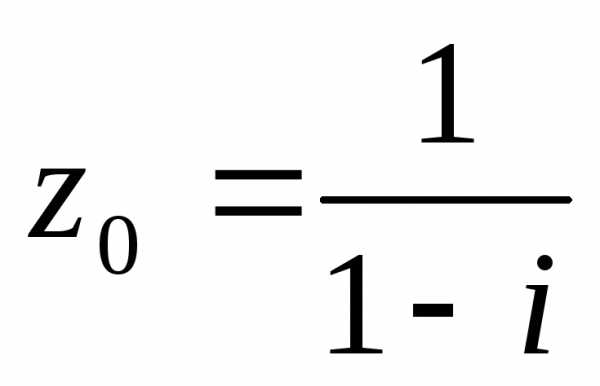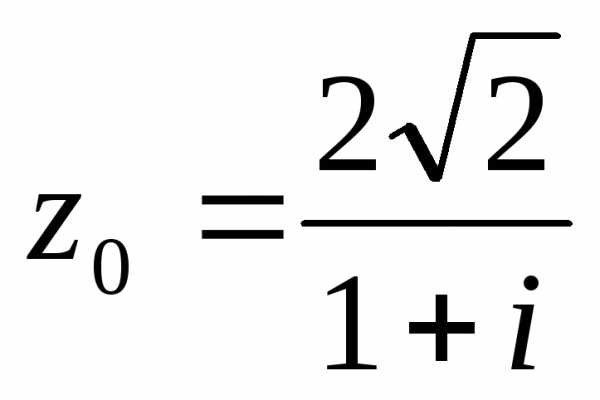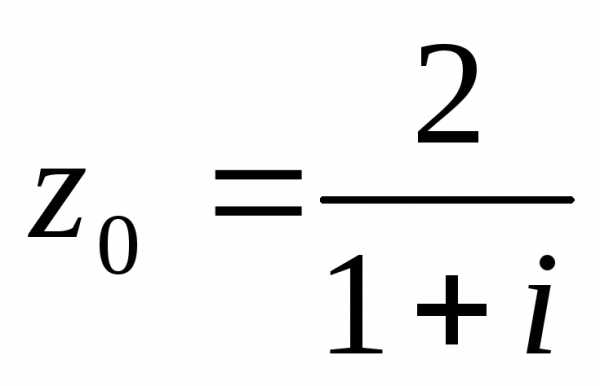As we know that the diagonals of rhombus are equal in length & intersect each other normally. Distance of each vertex from the origin is $sqrt{3^2+4^2}=5$.
Thus assuming the rhombus ABCD, the vertex C opposite to $Aequiv (3, 4)$ can be easily determined as the moi-point of AC is $(0, 0)$ Hence, $C(-3, -4)$. Now, assume any vertex say $(x, y)$ on the other diagonal BD. Since, the semi-diagonal OB is normal to OA, we get $$left(frac{y-0}{x-0}right)left(frac{4-0}{3-0}right)=-1 implies y=-frac{3}{4}x tag 1$$ Since $OB=OA=sqrt{3^2+4^2}=5$, we get
$$sqrt{(x-0)^2+(y-0)^2}=5 implies x^2+y^2=25$$ Setting the value of $y$, we get $$x^2+left(-frac{3}{4}xright)^2=25 implies x^2=16 implies x=pm 4$$$$ x=4quad implies y=-frac{3}{4}(4)=-3$$ $$ x=-4quad implies y=-frac{3}{4}(-4)=3$$ Thus, all the unknown vertices of rhombus ABCD are $Bequiv (4, -3)$, $Cequiv(-3, -4)$ & $Dequiv(-4, 3)$
2x-5y-1=0
y = 2/5x-1/5 (1)
2x-5y-34=0
y = 2/5x-34/5 (2)
x+3y-6=0
y = -1/3x+2 (3)
Прямые (1) и (2) параллельны, т.к. угловые коэффициенты равны. Значит (1) и (2) — противоположные стороны ромба.
Найдём координаты точек пересечения диагонали со сторонами ромба:
1) 2/5x-1/5 = -1/3x+2
×15
6x-3 = -5x+30
6x+5x = 30+3
11x = 33
x = 3
y(3) = 2/5*3-1/5 = 6/5-1/5 = 5/5 = 1
A(3; 1)
2) 2/5x-34/5 = -1/3x+2
×15
6x-102 = -5x+30
6x+5x = 102+30
11x = 132
x = 12
y(12) = 2/5*12-34/5 = 24/5-34/5 = -10/5 = -2
C(12; -2)
AC — диагональ ромба. Вторая диагональ BD проходит перпендикулярно AC через её середину. Найдём точку O пересечения диагоналей. Это — середина отрезка AC.
O((3+12)/2; (1-2)/2) = (15/2; -1/2) = (7,5; -0,5)
Найдём уравнение диагонали BD. Это прямая, проходящая через точку O перпендикулярно AC. Угловой коэффициент этой прямой k = 1/3.
y-(-0,5) = -1/(-1/3)
·(x-7,5)
y+0,5 = 3*(x-7,5)
y+0,5 = 3x-22,5
y = 3x-23
Найдём точки пересечения диагонали BD с прямыми (1) и (2). Это и будут координаты вершин B и D.
1) 2/5x-1/5 = 3x-23 ×5
2x-1 = 15x-115
15x-2x = 115-1
13x = 114
x = 114/13 = 8 10/13
y(114/13) = 2/5*114/13-1/5 = 228/65-13/65 = 215/65 = 43/13 = 3 4/13
B(8 10/13; 3 4/13)
2) 2/5x-34/5 = 3x-23 ×5
2x-34 = 15x-115
15x-2x = 115-34
13x = 81
x = 81/13 = 6 3/13
y(81/13) = 2/5*81/13-34/5 = 162/65-442/65 = -310/65 = -62/13 = -4 10/13
D(6 3/13; -4 10/13) Ответ: A(3; 1), B(8 10/13; 3 4/13), C(12; -2), D(6 3/13; -4 10/13)
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: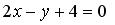

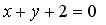
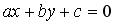
.
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
.
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
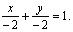
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
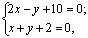
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка 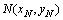
.
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору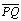
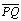
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору 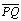
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
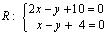
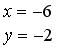
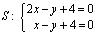

Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0,

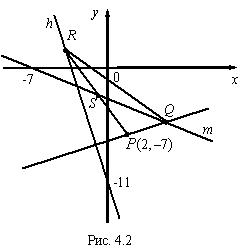
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h :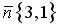
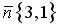

Находим координаты точки Q — точки пересечения прямых PQ и m :
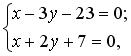
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
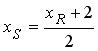
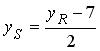
Точка S лежит на медиане m , значит,
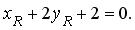
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему:
3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P :
Аналогично, составим уравнение прямой RQ :
Ответ: x — 3 y — 23 = 0, 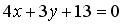
задачи на прямую на плоскости

Ответ:
12°30′;
BAC=28°; 
Задача №9
Вычислить координаты вершин ромба, если
известны уравнения двух его сторон:
x+2y=4 и х+2у=10 и уравнение одной из его
диагоналей у=х+2
Дано:
Найти: А,В,С и D.
Решение
а) Решим 2 системы из 2 линейных уравнений.
1) Первая x+2y=4 и y=x+2 даст одну вершину А
ромба:
.
Вторая х+2у=10 и у=х+2 даст другую вершину
С ромба:
.
б) Нашли середину диагонали: (1;3)
в) используя свойство ромба найдем его
вторую диагональ (она будет перпендикулярна
заданной) у=-x+b, подставим координаты
середины отрезка АС — точки М пересечения
координат М(1;3) найдем b=4 т.е вторая
диагональ
у=-х+b,
b=x+y=1+3=4,
b=4.
y=-x+4.
г) Найдем точки пересечения ее со
сторонами — это будут две другие вершины.
Решим 2 системы из 2 линейных уравнений.
1) Первая x+2y=4 и y=-x+4 даст одну вершину В
ромба:
2) Вторая х+2у=10 и у=-х+4 даст другую вершину
Dромба:
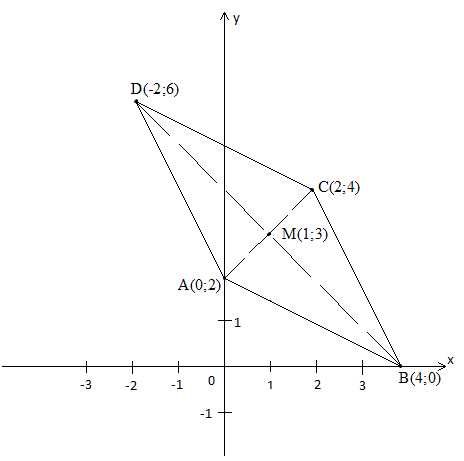
Ответ А(0;2), В(4;0), С(2;4), D(-2;6)
studfiles.net
§ 5 Примеры решения задач и задачи для самостоятельного решения
Основные
методы составления уравнений прямых
наглядно можно продемонстрировать на
примере построения уравнений линейных
элементов треугольника .
Пример15.
Треугольник
Найти:
-
медиану
;
-
среднюю
линию
;
-
высоту
;
-
биссектрису
;
-
центр
описанной окружности.
Решение.
-
Найдем
медиану
.
Вычислим координаты точки
середины отрезка
.
.
Уравнение
по двум точкам:
.
-
Найдем
среднюю линию
.
Способ
1. Вычислим
координаты середины стороны
точки

Уравнение
.
Способ
2. Найдем

точке
которого можно взять вектор
.
Вычислим:
.
Тогда:
Очевидно,
что для

первом способе.
-
Уравнение
высоты
найдем по точке и перпендикулярному
вектору, в качестве которого можно
взять вектор.
.
-
Биссектрису
можно найти разными способами (Рис.
10). Но, если числовые данные в задаче
специально не подобраны, то все эти
способы приводят к громоздким
вычислениям. Наиболее легким для
запоминания является способ, основанный
на следующем факте:
вектор
суммы векторов одинаковой длины идет
в точности по биссектрисе угла,
образованного этими векторами (свойство
ромба).
Поскольку
требуется найти биссектрису угла

то возьмем два вектора, исходящих именно
из этой вершины:и.
Вычислим их длины:
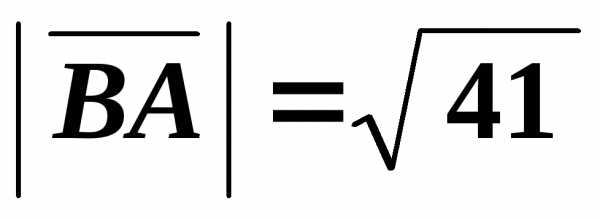
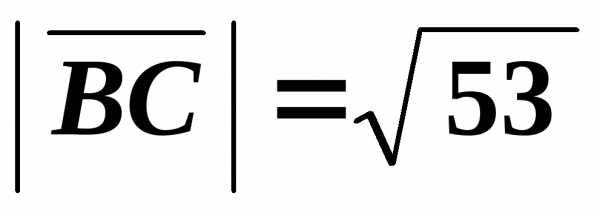
Очевидно,
что их длины не равны. А теперь от
векторов

перейдем к их ортам
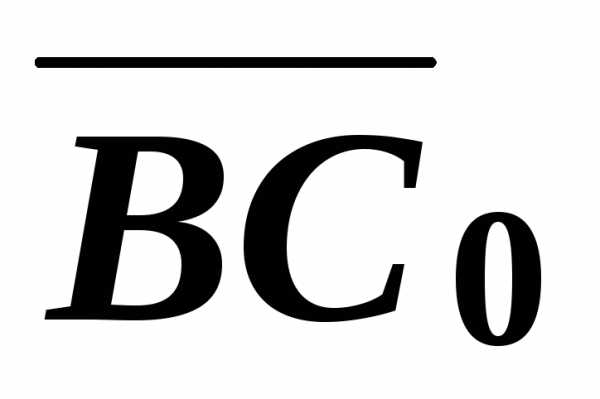
векторам с тем же направлением, но
одинаковой единичной длины.
;
.
Построим
новый вектор
.
Этот
вектор уже можно использовать в качестве
направляющего для биссектрисы, но
работать с ним нелегко. Вместо него
можно взять другой вектор, попроще.
Корни,
конечно, никуда не исчезли, но, по крайней
мере, не стало дробей.
По
формуле (9) имеем:
Если
Вам не нравится отрицательный коэффициент
при

умножьте все уравнение на (1
):
-
Найдем
центр окружности, описанной вокруг
треугольника
.
Он,
как известно, находится в точке
пересечения любых двух серединных
перпендикуляров треугольника
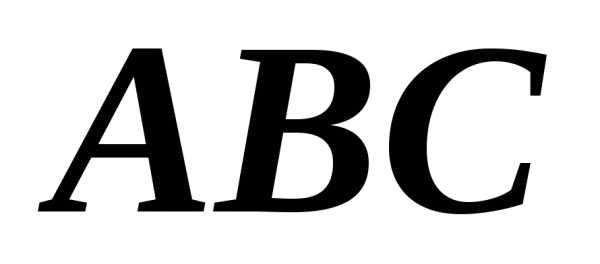
Поскольку ранее
были найдены координаты середин сторон

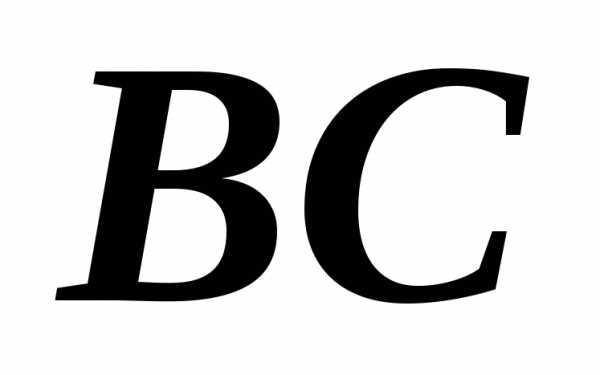
найдем уравнения серединных перпендикуляров
именно к этим сторонам:
.
Для
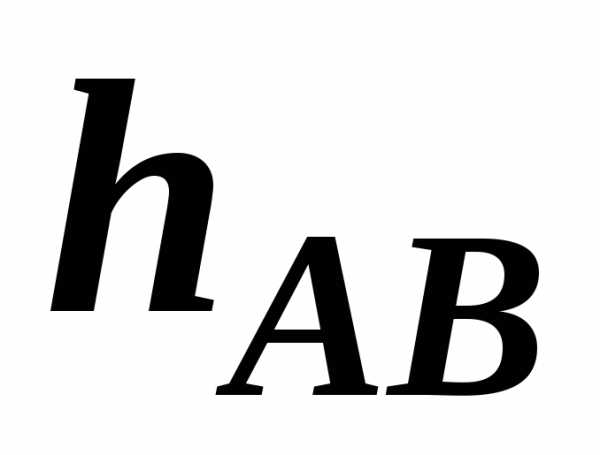
|
точка перпендикулярен |
Для
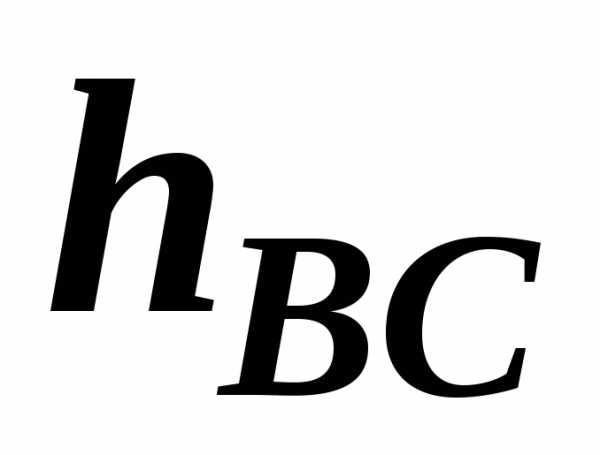
|
точка перпендикулярен |
Найдем
точку пересечения полученных серединных
перпендикуляров:
и
Воспользуемся
формулами Крамера:
;
;
.
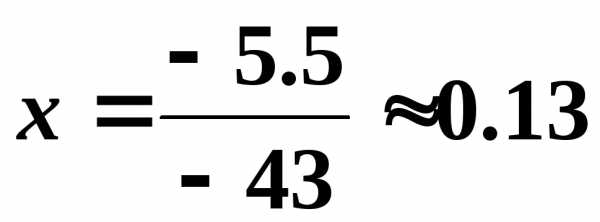
Задачи
для самостоятельного решения
-
Известны уравнения двух сторон ромба ,и уравнение одной из его диагоналей. Составить уравнение второй диагонали.Ответ: .
-
Известны
уравнения двух сторон ромба
,и уравнение одной из его диагоналей.
Составить уравнение второй
диагонали.Ответ: . -
Даны
уравнения двух сторон параллелограмма
,и точка пересечения его диагоналей.
Найти уравнения двух других сторон.
Ответ: ,. -
Даны
вершины треугольника
,и.
Составить уравнение перпендикуляра,
опущенного из вершинына
биссектрису внутреннего угла при
вершине.Ответ: .
-
Найти
точку
,
симметричную точкеотносительно прямой, проходящей
через точкии.
Ответ:.
-
Точки
и
являются
противоположными вершинами квадрата.
Определить координаты двух других
вершин квадрата.
Ответ: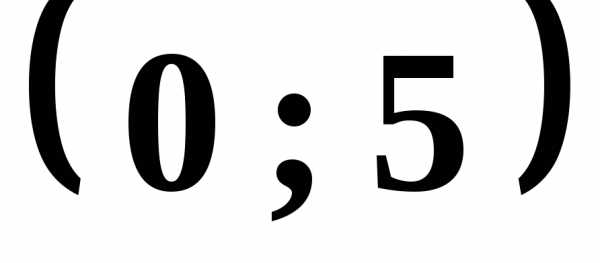
-
Найти прямые,
принадлежащие пучку
и
перпендикулярные основным прямым
пучка.
Ответ: ,.
-
Даны стороны
треугольника:
;и.
Составить уравнения медианы ,
проходящей через вершину,
и высоты, проходящей через вершину.Ответ:
,
.
-
Составить
уравнения трех сторон квадрата, если
известно, что четвертой стороной
являются отрезок прямой
,
концы которого лежат на осях координат.
Ответ: ,,или.
-
Доказать,
что четырехугольник с вершинами
,,
и
–
трапеция. Найти точку пересечения
средней линии трапеции и высоты,
опущенной из вершины С на сторону
.
Ответ:
-
Вершины
четырехугольника:
,,,.
Доказать, что этот четырехугольник
ромб. Найти точку пересечения
перпендикуляра из вершины
на
сторонус прямой, проходящей через вершину
и середину.
Ответ:
-
Даны
три из четырёх вершин трапеции
:.
Известно, что диагонали трапеции
взаимно перпендикулярны. Найти
координаты вершиныэтой трапеции.
Ответ:
ГЛАВА
2. Плоскость
§
1 Вступление
В
аналитической геометрии плоскость

пространстве, координаты которых
удовлетворяют уравнению
.
общее уравнение
плоскости;
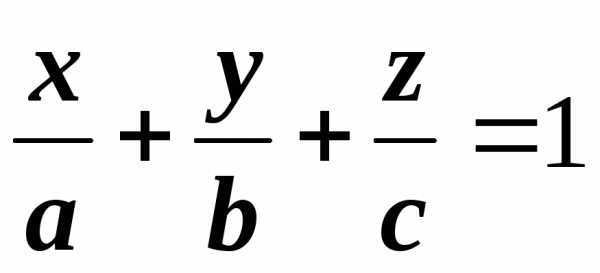
плоскости в отрезках,
где


осью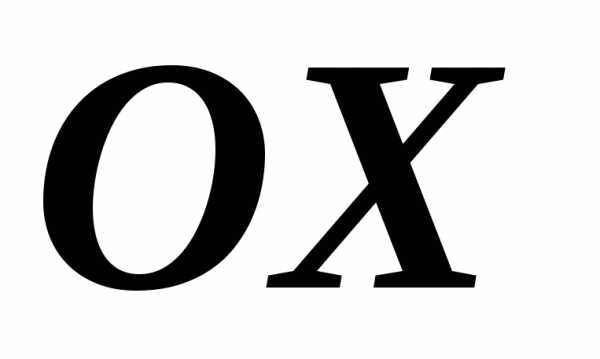

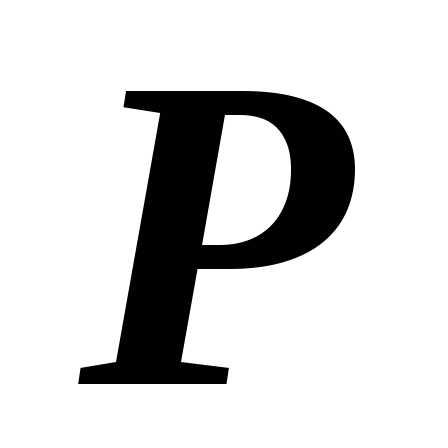
осью
а
пересечения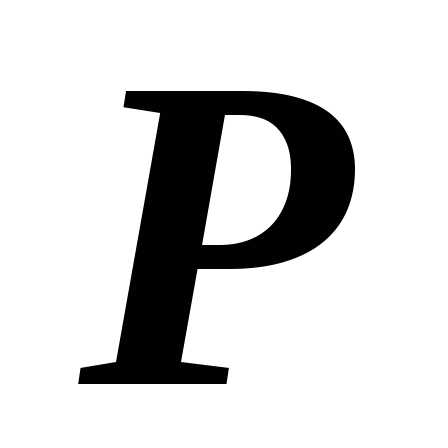
осью
§
2 Вывод уравнения плоскости при разных
способах
ее задания.
-
Уравнение
плоскости, проходящей через три заданных
точки
,и,
не лежащие на одной прямой.
(15)
Чтобы
получить общее уравнение плоскости
,
нужно символьно вычислить этот
определитель, например, разложив его
по первой строке.
Пример16.
Даны вершины тетраэдра:
,,и.
Найти уравнение грани
Р
D(-1;0;5)
С(2;2;0)
А(3;-1;1)
В(-4;1;0)
ешение.Замечу, что эту задачу можно решать
«вслепую», без чертежа. Но для лучшего
понимания методов решения, чертеж (хотя
бы схематический) лучше все-таки
нарисовать.
Обозначимпроизвольная точка
плоскости, в которой лежит основание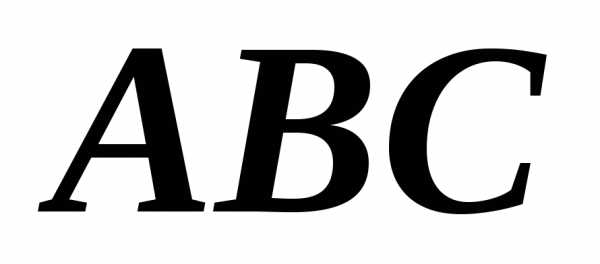
-
.
Окончательно
.
(16)
Пример17.Даны вершины тетраэдра:,,и.
Найти уравнение плоскости, проходящей
через вершину

Решение.Искомая плоскость
плоскость

то векторперпендикулярен плоскости треугольника
Точка.
Тогда
.
Пример
18.
Известно, что точки:
исимметричны относительно некоторой
плоскости
Найти уравнение этой плоскости.
Р
B
ешение.
Искомая плоскость изображена на Рис.14.
Поскольку по условию точки


относительно плоскости
то они лежат на перпендикуляре к этой
плоскости, проходящем через

Так как

от плоскости
то эта плоскость проходит через середину
отрезка
точку

Нарисуем вектор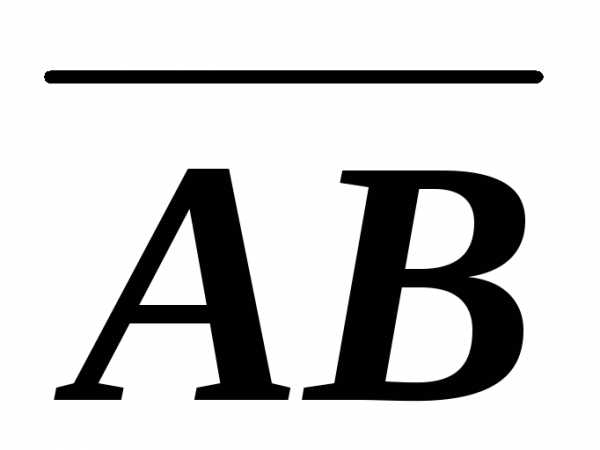
Вычислим координаты точки
уравнение искомой плоскости
/
поделим на (
4) /
.
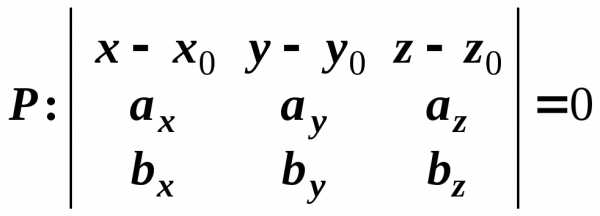
Замечание.
Решение многих задач на составление
уравнения плоскости на практике сводится
к поиску трех компланарных векторов.
Их смешанное произведение, как известно,
равно нулю. В координатах смешанное
произведение вычисляется с помощью
определителя 3-го порядка, строки
которого и есть координаты этих трех
векторов. Именно в этом и заключается
смысл формул (15) и (17 ).
Пример
19.
Составить уравнение плоскости, проходящей
через точку
параллельно двум векторами.
Решение.
Прежде всего заметим, что векторы

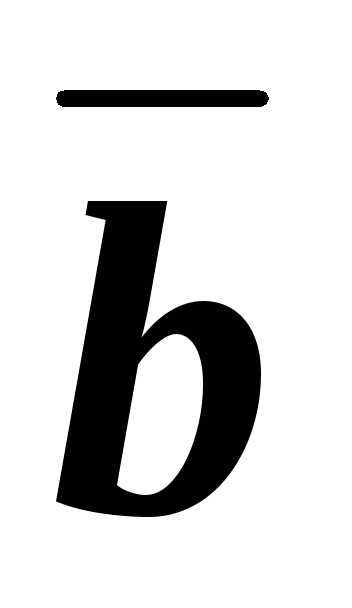
не пропорциональны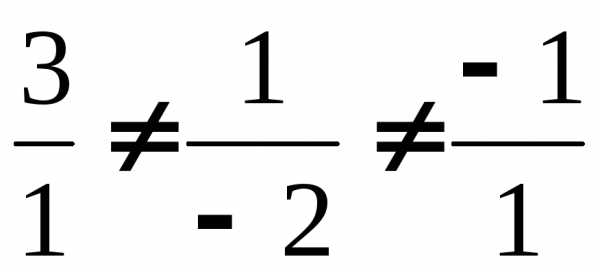
произвольная точка искомой плоскости.
Нарисуем вектор

По условию искомая плоскость параллельна
векторам

свою очередь означает, что параллельным
переносом векторы
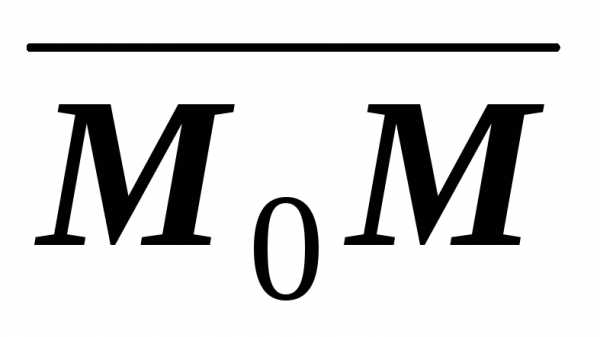
Следовательно все три вектора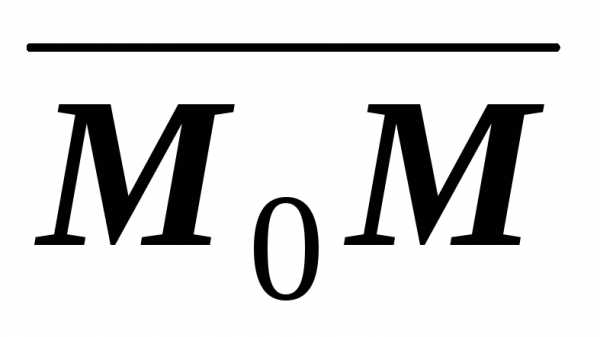

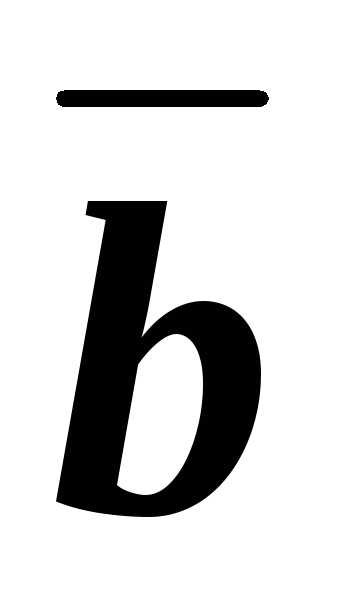
что в координатах дает уравнение
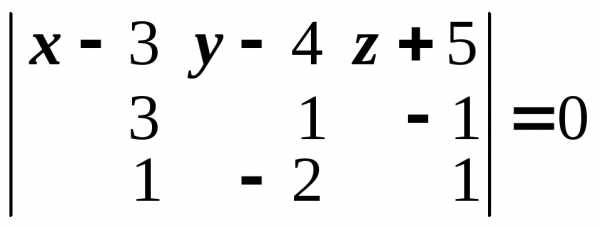
или
.
-
Уравнение
плоскости, проходящей через две заданных
точки
,параллельно заданному вектору
(18)
Пример
20.
Известно, что пространственная прямая
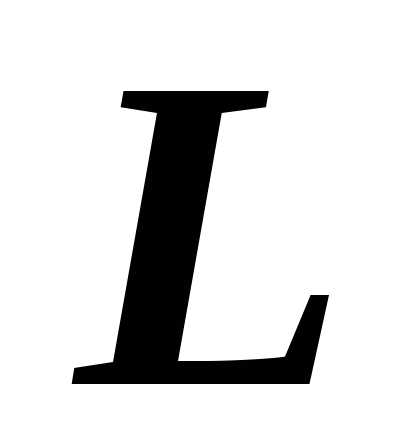
проходящая через точку,
пересекает плоскостьв точке.
Найти уравнение плоскости
проектирующей прямую
данную плоскость
Решение.
Две точки, через которые проходит
искомая плоскость

уже имеются
это точки

По этим точкам можно ввести вектор,
заведомо лежащий в искомой плоскости
Далее, как всегда, введем точку
произвольную точку искомой плоскости.
По ней и по точке, например,

еще один вектор, также лежащий в искомой
плоскости, а именно.
Осталось найти вектор, которому плоскость
или, что то же самое, который параллелен
этой плоскости. Таковым является вектор
нормальный вектор данной плоскости

Введенные три вектора компланарны, а
значит их смешанное произведение,
что в координатах дает уравнение:

studfiles.net
Контрольная работа «аналитическая геометрия» Контрольные варианты к задаче 1
Даны координаты
вершин треугольника АВС. Требуется:
1) вычислить
длину стороны ВС;
2) составить
уравнение линии ВС;
3) составить
уравнение высоты, проведенной из вершины
А;
4) вычислить
длину высоты, проведенной из вершины
А;
5) найти точку
пересечения медиан;
6) вычислить
внутренний угол при вершине В;
7) найти координаты
точки М, расположенной симметрично
точке А относительно прямой ВС.
|
1. |
. |
2. |
. |
|
3. |
. |
4. |
. |
|
5. |
. |
6. |
. |
|
7. |
. |
8. |
. |
|
9. |
. |
10. |
. |
|
11. |
. |
12. |
. |
|
13. |
. |
14. |
. |
|
15. |
. |
16. |
. |
|
17. |
. |
18. |
. |
|
19. |
. |
20. |
. |
|
21. |
. |
22. |
. |
|
23. |
. |
24. |
. |
|
25. |
. |
26. |
. |
|
27. |
. |
28. |
. |
|
29. |
. |
30. |
. |
Контрольные варианты к задаче 2
1. Вершина
квадрата
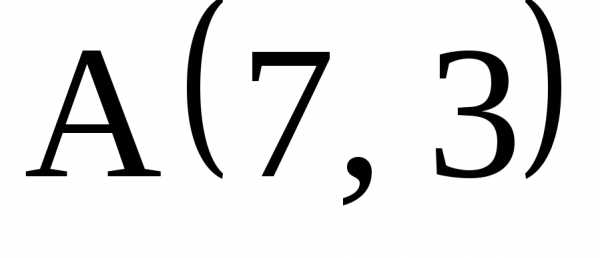
сторона СD
лежит на прямой, отсекающей на осях
координат отрезки
.
Написать уравнение стороны АД (Квадрат
АВСD).
2. В треугольнике
АВС даны уравнения: высоты
,
высоты
и стороны.
Составить уравнение третьей высоты.
3. Найти точку,
симметричную точке
относительно прямой.
4. Составить
уравнение прямой, проходящей через
точку пересечения прямых
и
и образующей угол в
прямой.
5. Через точку
пересечения прямых
провести прямую перпендикулярно прямой.
6. В треугольнике
АВС даны уравнения: стороны АВ
и высот.
Составить уравнения двух других сторон
треугольника.
7. Вычислить
координаты вершин ромба, если известны
уравнения двух его сторон ()
и уравнение одной из его диагоналей.
8. Из точки
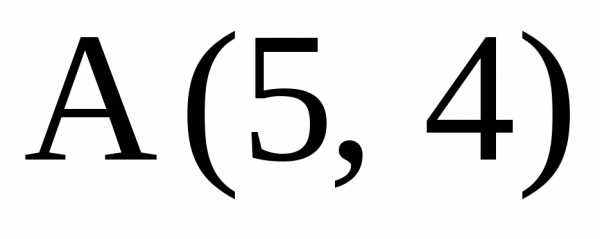
уравнения падающего и отраженного
лучей.
9. Под каким
углом к оси Ох наклонена прямая, проходящая
через точки
.
10. В квадрате
АВСD
даны вершина
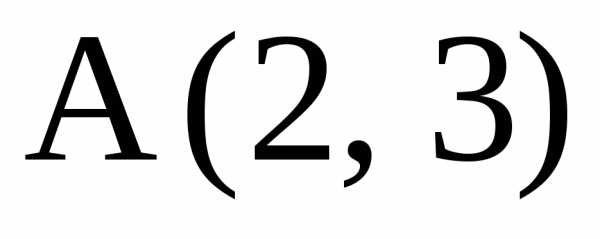

точка пересечения диагоналей. Найти
уравнения сторон квадрата, не проходящих
через верши-
ну А.
11. Даны точки
.
Отрезок АС разделен точкойD
в отношении
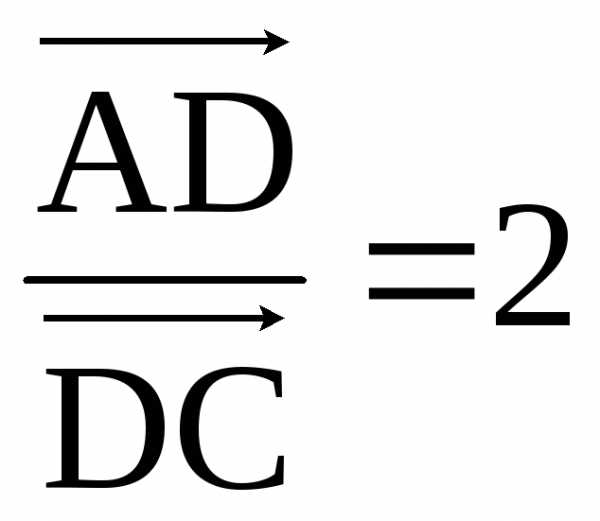
Найти расстояние от точки А до прямой
ВD.
12. Отрезок
прямой
,
заключенный между осями координат,
является диагональю квадрата. Найти
уравнение одной (любой) стороны квадрата.
13. Через точку
пересечения прямых
провести прямую перпендикулярно прямой.
14. Даны уравнения
двух сторон параллелограмма:
и точка пересечения диагоналей
Составить уравнения двух других сторон
параллелограмма.
15. Составить
уравнения прямых, проходящих через
точку
и составляющих угол
16. Даны уравнения
двух сторон параллелограмма
-и точка пересечения
его диагоналей
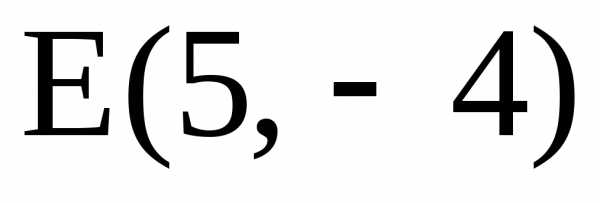
Составить уравнения
двух других его
сторон.
17. Даны середины
противоположных сторон квадрата
.
Написать уравнения двух сторон квадрата,
на которых лежат точки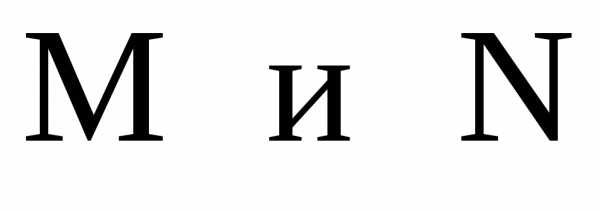
18. Провести
прямую так, чтобы точка

между осями координат. Составить
уравнение этой прямой.
19. Даны две
точки:
.
Через середину отрезка АВ провести
прямую, отсекающую от оси Ох отрезок,
вдвое больший, чем отрезок на оси Оу.
20. В треугольнике
АВС даны вершины:
.
Определить: а) угол между стороной АВ
и медианой стороны ВС; б) длину высоты,
опущенной из вершины С.
21. Составить
уравнения катетов прямоугольного
равнобедренного треугольни-
ка, зная уравнение
гипотенузы
и вершину прямого угла.
22. Составить
уравнение прямой, проходящей через
точку
и отсекающей от координатного угла
треугольник площадью 8 дм2.
23. В треугольнике
АВС даны вершины:
.
Найти точку, симметричную точке В
относительно стороны АС.
24. В треугольнике
АВС даны вершины:
.
Найти угол между медианой АМ и высотой
ВН.
25. Даны точки
.
На отрезке ОА ( О – начало координат),
построить параллелограмм ОАСД, диагонали
которого пересекаются в точке В. Написать
уравнения сторон и диагоналей
параллелограмма.
26. Под каким
углом к оси Ох наклонена прямая, проходящая
через точки
?
27.Составить
уравнение прямой, проходящей через
точку пересечения прямых
и образующую с осью Ох угол, вдвое больший
угла, образованного с той же осью прямой.
28. Найти точку,
симметричную точке
относительно прямой.
29. Прямая
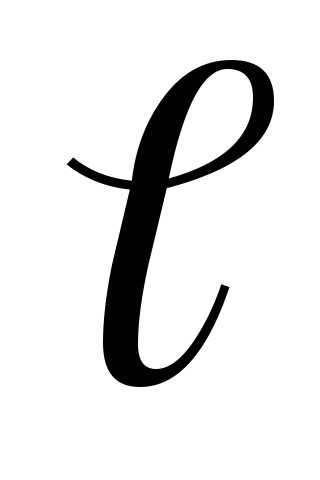
Найти точку, симметричную точке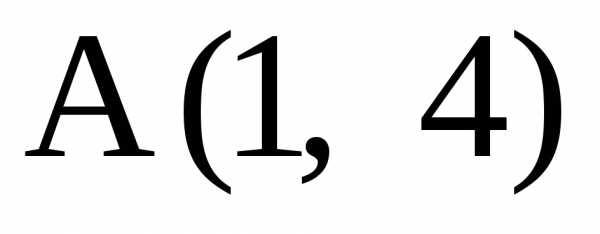
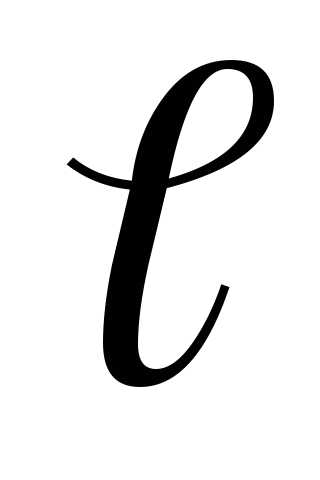
30. Даны уравнения
двух сторон параллелограмма:
-и одна из его
вершин
.
Найти точку пересечения его диагоналей.
studfiles.net
Задачи для контрольных работ
Контрольная
работа №1
Основы линейной
алгебры
Задание 1.
Найти матрицу С=.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Задание 2.
Решить систему линейных алгебраических
уравнений двумя способами: 1) методом
Крамера; 2) с помощью обратной матрицы.
1.

3.

5.
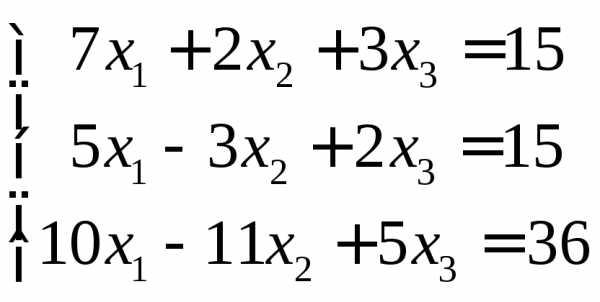
7.
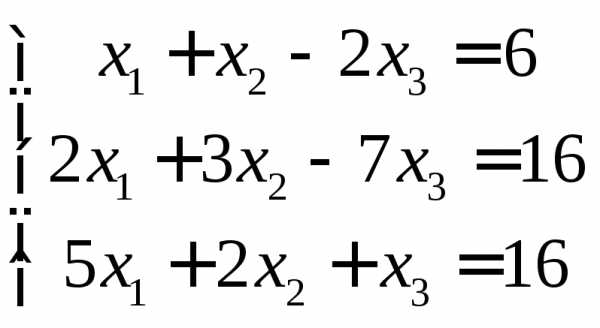
9.
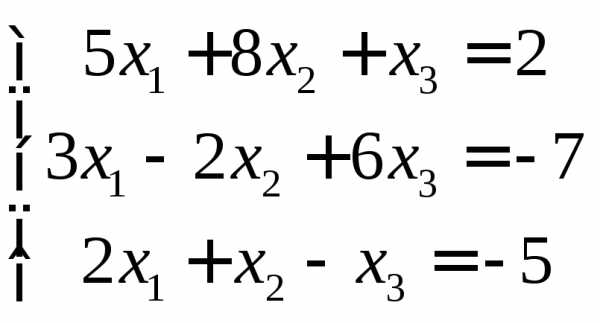
Задание 3.
Решить систему методом Гаусса.
1.
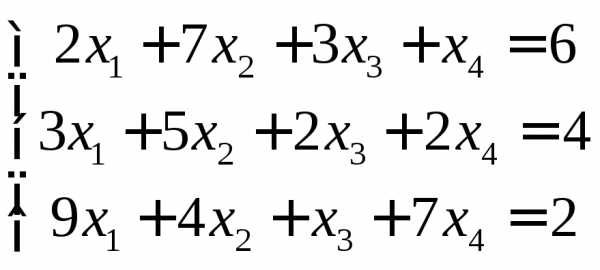
3.

5.
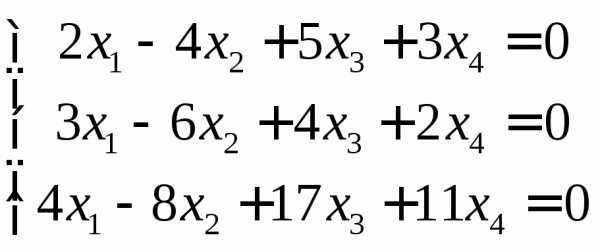
7.
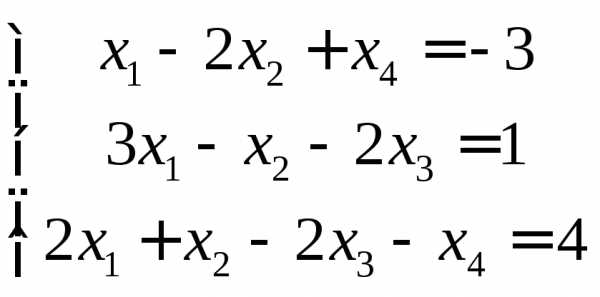
9.
10.
Задание 4.
Найти собственные числа и собственные
векторы матрицы

1.
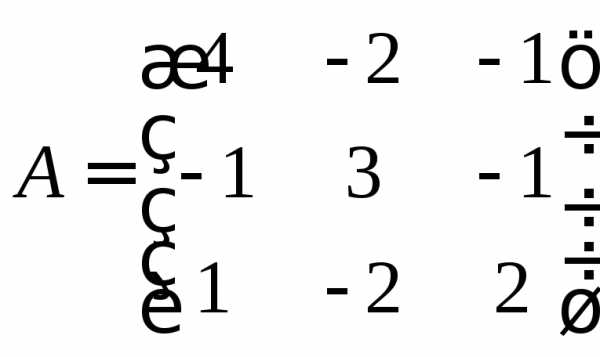
3.

5.
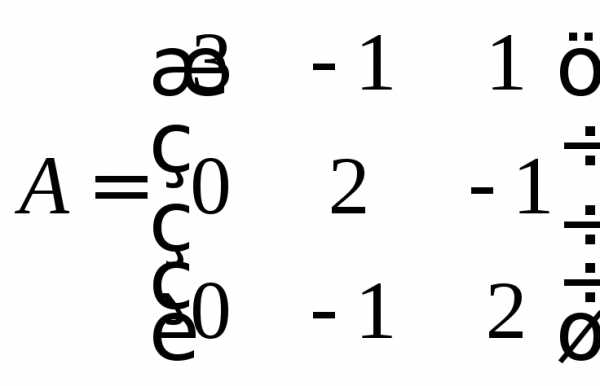
7.
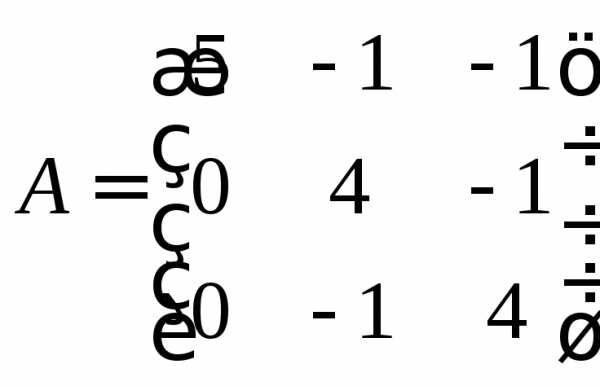
9.
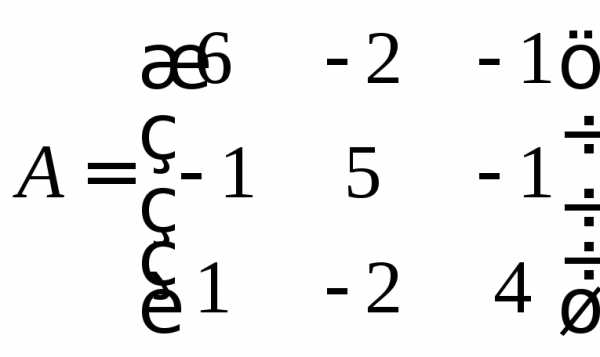
Контрольная
работа №2
Элементы векторной
алгебры и аналитической геометрии.
Комплексные числа
Задание 1.
Даны координаты вершин пирамиды
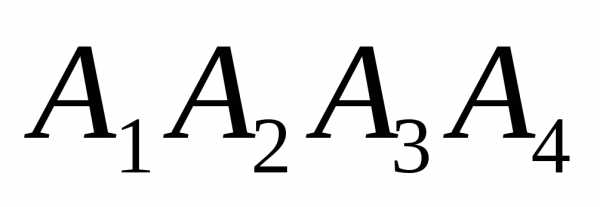
Требуется найти: 1) длину ребра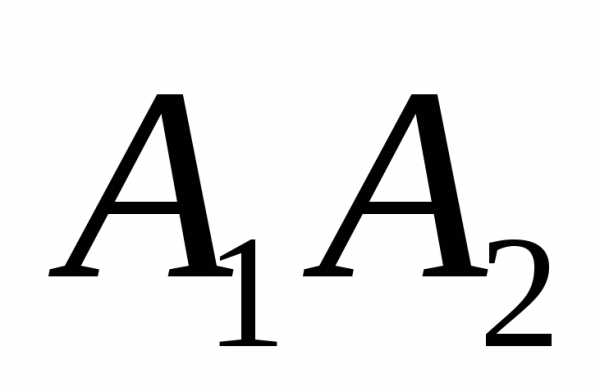
2) угол между ребрами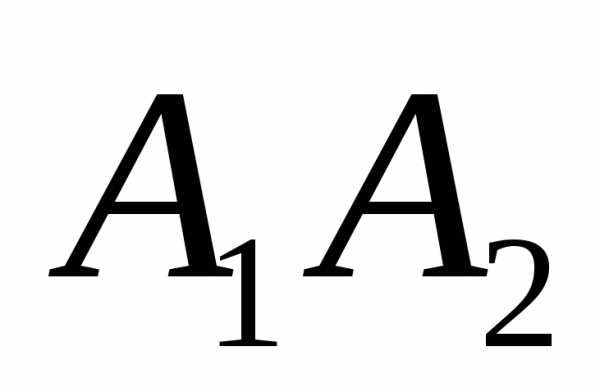

3) угол между ребром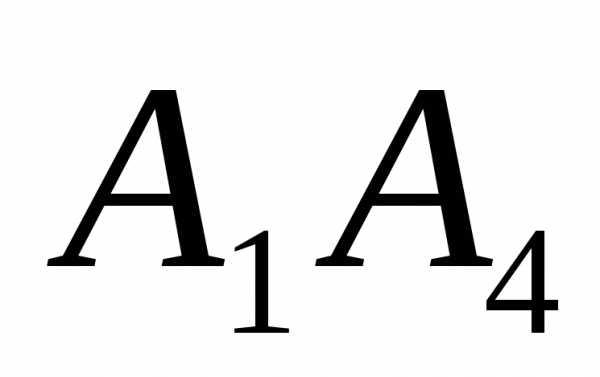
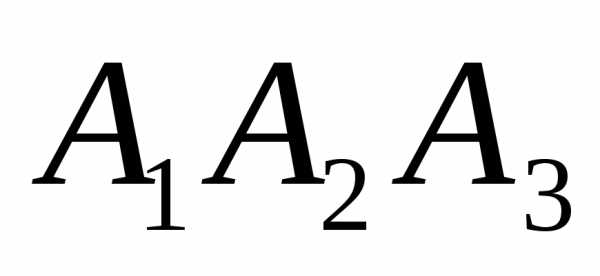
4) площадь грани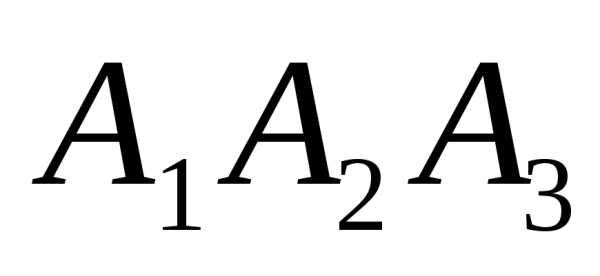
5) объем пирамиды; 6) уравнения прямой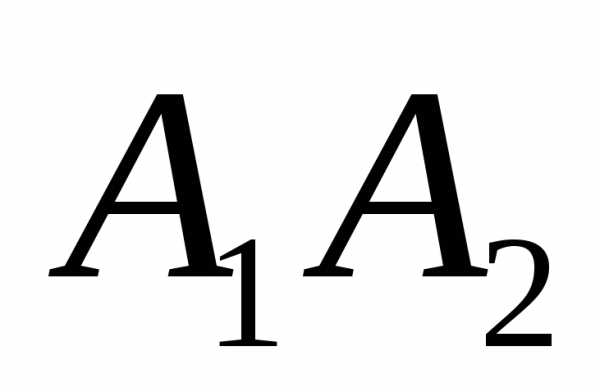
7) уравнение плоскости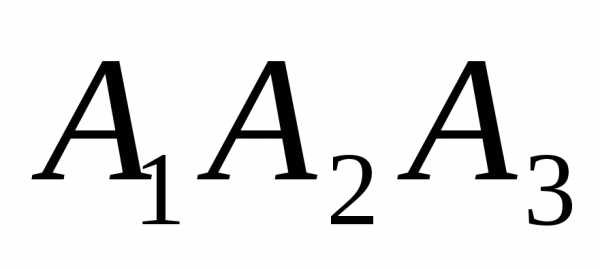



Сделать чертеж.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Задание 2.
-
Написать уравнения
сторон треугольника АВС,
если задана его вершина
и уравнения двух медиани
Сделать
чертеж. -
Написать уравнения
сторон треугольника, зная одну его
вершину
,
а также уравнения высотыи медианы,
проведенных из различных вершин. Сделать
чертеж. -
Найти внутренние
углы треугольника, если даны уравнения
его сторон
и,
и основаниевысотыAD.
Сделать чертеж. -
Две стороны
параллелограмма заданы уравнениями
и.
Диагонали его пересекаются в начале
координат. Написать уравнения двух
других сторон параллелограмма и его
диагоналей. Сделать чертеж. -
Найти вершины
прямоугольного равнобедренного
треугольника, если дана вершина прямого
углаи уравнение гипотенузыСделать
чертеж. -
Даны две вершины
треугольника
и
и точка пересечения высот
.
Найти третью вершинуС.
Сделать чертеж. -
Стороны АВ
и ВС
параллелограмма заданы уравнениями
и,
диагонали его пересекаются в точке.
Найти длины его высот. Сделать чертеж. -
Вычислить координаты
вершин ромба, если известны уравнения
двух его сторон:
и,
и уравнение одной из его диагоналей:.
Сделать чертеж. -
Составить уравнения
сторон треугольника, зная одну его
вершину
,
и уравнения высоти,
гдеМ-точка
пересечения высот. Сделать чертеж. -
В треугольнике
АВС
даны уравнение стороны,
уравнение высоты,
уравнение высоты,
гдеМ-точка
пересечения высот. Написать уравнения
сторон АС,
ВС и высоты
СМ.
Сделать чертеж.
Задание 3.
-
Написать уравнение
кривой, каждая точка которой находится
на одинаковом расстоянии от точки
и от оси
.
Сделать чертеж. -
Написать уравнение
кривой, сумма квадратов расстояний от
каждой точки которой до точек
и
равна 50. Сделать чертеж.
-
Написать уравнение
кривой, расстояние от каждой точки
которой до точки
вдвое меньше расстояния до точки.
Сделать чертеж. -
Написать уравнение
кривой, модуль разности расстояний от
каждой точки которой до точек
иравен 4. Сделать чертеж.
-
Написать уравнение
кривой, каждая точка которой находится
на одинаковом расстоянии от точки
и от оси
.
Сделать чертеж. -
Написать уравнение
кривой, каждая точка которой отстоит
от точки
вдвое дальше, чем от прямой
.
Сделать чертеж. -
Написать уравнение
кривой, для каждой точки которой
расстояние от точки
вдвое меньше расстояния от прямой
.
Сделать чертеж. -
Написать уравнение
кривой, сумма расстояний от каждой
точки которой до точек
и
равна 2
.
Сделать чертеж. -
Написать уравнение
кривой, сумма квадратов расстояний от
каждой точки которой до точек
иравна 27. Сделать чертеж.
-
Составить уравнение
кривой, для каждой точки которой
расстояния от начала координат и от
точки
относятся как 3:2. Сделать чертеж.
Задание 4.
Дана функция
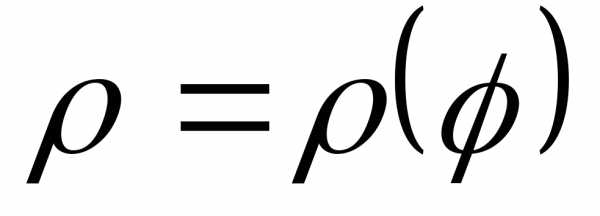
Требуется:
1) построить график
функции в полярной системе координат
по точкам, давая

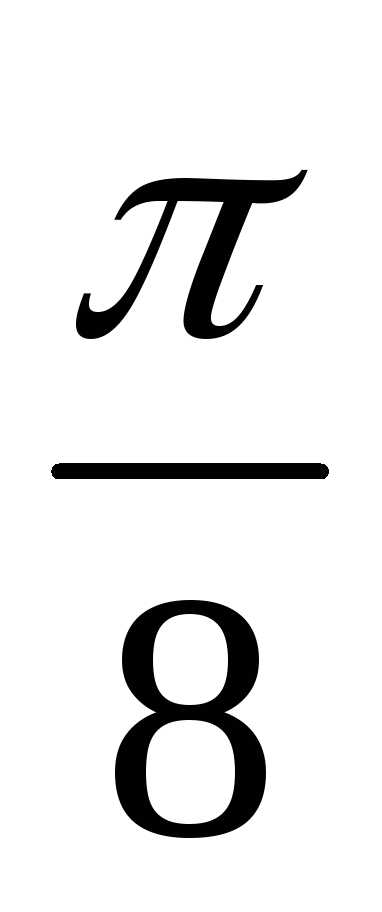
начиная от
2) найти уравнение линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс — с полярной осью; 3) по
полученному уравнению определить, какая
это будет линия; 4) сделать чертеж.
1.

3.
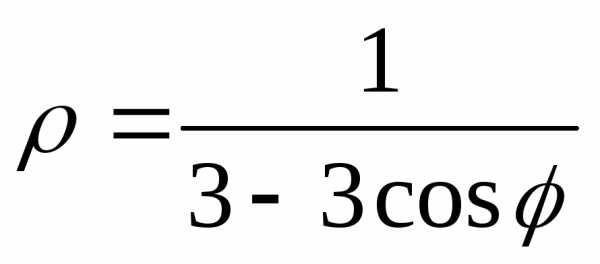
5.
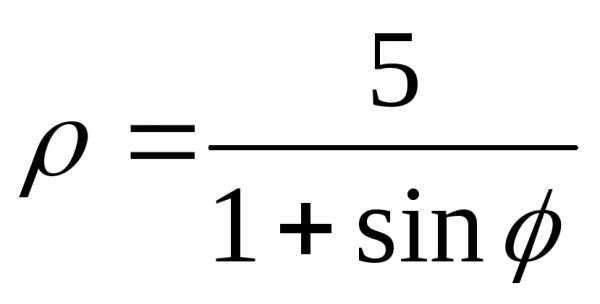
7.
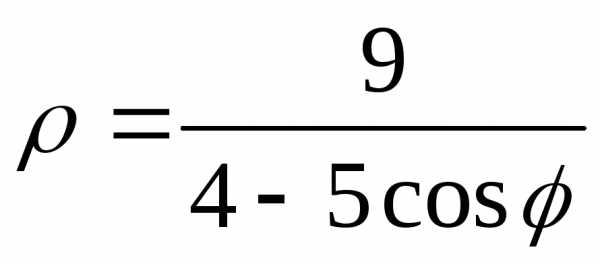
9.
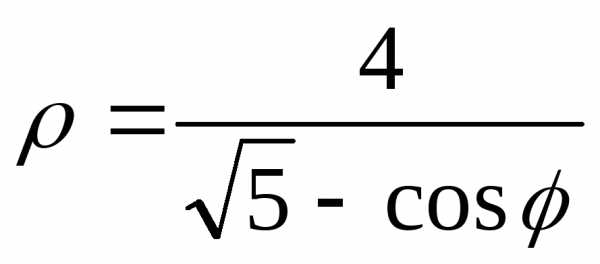
Задание 5.
Дано комплексное число
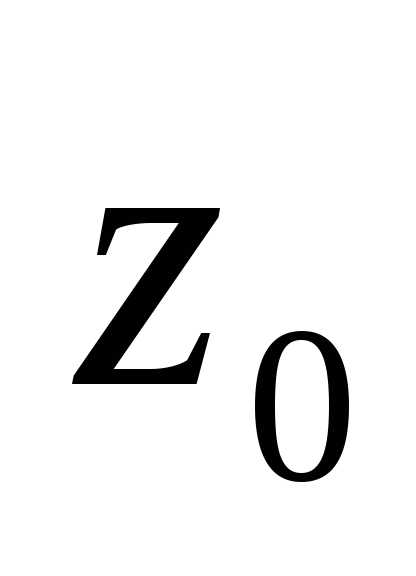
Требуется: 1) записать число
формах; 2) найти все корни уравнения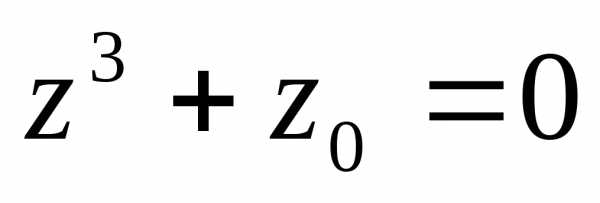
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
studfiles.net
An.Geom-1
Томский политехнический университет
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО ТЕМЕ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Часть 1. Прямая на плоскости
Рожкова О.В. Внутрикафедральное издание,
Рег. №18 от 05.02.09
|
Вариант №1 |
|
|
1.) |
Дана прямая 5x + 4y −3= 0 . Найти 1) направляющий вектор прямой, 2) угловой |
|
коэффициент прямой, 3) отрезки отсекаемые прямой на осях координат. |
|
|
2.) |
Две стороны квадрата лежат на прямых 3x + 4y + 22= 0, 3x + 4y −13= 0. |
|
Вычислить площадь квадрата. |
|
|
3.) |
Вычислить координаты вершин ромба, если известны уравнения двух его сторон |
|
x − 2y +5= 0,x − 2y −5= 0 и одной из диагоналейx +8y −5= 0. |
|
Вариант №2 |
|
|
1.) |
Найти угол между прямыми 3x − 2y +5= 0,x −5y +8= 0. |
|
2.) |
Даны три вершины треугольника A(−1,3),B(3,−2),C(5,3). Составить уравнения : |
1)медианы, проведенной из вершины В,
2)высоты, опущенной из вершины С на сторону АВ,
3)прямой, проходящей через вершину А, параллельно стороне ВС.
3.) Провести прямую так, чтобы ее отрезок, заключенный между двумя данными прямыми: 2x + y −1= 0,x +3y + 2= 0, делился в точкеМ(-1,0)пополам.
Вариант №3
|
1.) |
Найти уравнение прямой, проходящей через точку А(-8,0)под угломϕ = |
π |
к |
|
прямой 3x −2y +5= 0 . |
4 |
||
|
2.) |
Найти уравнение прямой, проходящей через точку пересечения прямых |
||
|
x −3y + 2= 0, 5x + 6y − 4= 0 и параллельной прямой 4x + y −7= 0 . |
|||
|
3.) |
Даны две вершины треугольника А(-1,3), B(3,2), уравнения стороны |
||
|
BC : 2x −3y = 0 и медианыAM :3x + y = 0. Составить уравнение высоты, |
опущенной из вершины С на сторону АВ.
Вариант №4
1.) Составить уравнение прямой, которая проходит через точку М(-3,2)и параллельна прямой 2x + y = 7.
2.) Через точку М(2,5) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делился в этой точке пополам.
3.) Составить уравнения сторон треугольника, зная одну из его вершин А(-1,3)и уравнения двух высот 3x − 4y +8= 0, 5x + 2y −8= 0.
Вариант №5
1.) Найти угол между прямыми 2x +3y −5= 0,x −3y −7= 0.
2.) Задан треугольник координатами вершин А(-1,-3),B(4,-5),C(2,1). Вычислить длину высоты, проведенной из вершины В.
3.) Найти координаты вершин параллелограмма, если известны уравнения двух его сторон 2x −3y +1= 0,x + y − 2= 0 и точка пересечения диагоналей М(3,32).
Вариант №6
1.) Дана прямая 3x −5y −7= 0.Составить уравнение прямой проходящей через точку
А(2,-1)параллельно данной прямой.
2.) Найти угол между прямой 2x −3y +6= 0 и прямой, проходящей через точки
М(4,-5),N(-3,2).
3.) Составить уравнения АС и ВС сторон треугольника АВС, если точка А(2,5), а уравнения высоты и биссектрисы, выходящих из вершин В и C соответственно: x − 2y + 7= 0, 4x + y −1= 0.
Вариант №7
1.) Дана прямая 3x − y + 4= 0. Указать: 1) нормальный вектор прямой;
2.) направляющий вектор прямой;
3) угловой коэффициент прямой. 2.) Даны вершины треугольника А(-10,-13),B(-2,3),C(2,1). Вычислить длину
перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
3.) Даны вершины А(-2,1),B(3,- 4) треугольника АВС и точка пересечения его высотК(5,-1).Составить уравнения сторон этого треугольника.
Вариант №8
1.) Составить каноническое уравнение прямой, проходящей через точку М(7,-2)параллельно биссектрисе координатных углов.
2.) Найти уравнение прямой, проходящей через начало координат и образующей с прямой y = 2x +3 угол 45o.
3.) Составить уравнения сторон треугольника, зная его вершину А(-6,3),уравнения высоты 7x +3y −5= 0 и медианы 9x + y −15= 0, проведенных из одной вершины.
Вариант №9
1.) Прямая проходит через точки М(-1,3)и N(2,5). Найти :
1) направляющий вектор прямой;
2.) нормальный вектор прямой;
3) угловой коэффициент прямой. 2.) Найти уравнение геометрического места точек, удаленных от прямой
3x − 4y +10= 0 на расстояние, равное 2.
3.) Найти внутренние углы треугольника, если даны уравнения его сторон AB 😡 −3y +3= 0,AC 😡 +3y +3= 0, и основаниеД(-1,3)высоты АД.
Вариант №10
1.) Луч света направлен по прямой y = 3x −6. Дойдя до оси абсцисс, он от нее
отразился. Определить точку встречи луча с осью ОX и уравнение отраженного луча.
2.) Вычислить угол между прямыми 5y + 4= 0,3x −3y −3= 0.
3.) Даны две смежные вершины параллелограмма А(-3,1)и В(2,2) и точка пересечения его диагоналей М(3,0). Составить уравнения высот параллелограмма, проведенных из вершины А.
Вариант №11
1.) Найти угол между прямыми y = 2x −5,y = −12 x +1.
2.) Дан треугольник с вершинами A(0;5), B(3;1), C(-6,-3).Найти уравнение медианы СЕ и биссектрисы АД.
3.) Даны уравнения двух сторон прямоугольника x −3y + 6= 0, 3x + y −12= 0 и точка
пересечения его диагоналей М(7;2). Составить уравнения двух других сторон прямоугольника.
Вариант №12
1.) Составить каноническое уравнение прямой, проходящей через точку А(2;-1)перпендикулярно к прямойy = −3x +1. Найти отрезки, отсекаемые этой прямой а
осях координат.
2.) Составить уравнение прямой, которая проходит через точку пересечения прямых x + y − 2= 0 и 3x + 2y −5= 0 перпендикулярно к прямой 3x + 4y −12= 0.
3.) В равнобедренном прямоугольном треугольнике даны координаты вершины острого угла А(-1;3)и уравнение противолежащего катета 2x −3y +1= 0.
Составить уравнения двух других сторон треугольника.
Вариант №13
1.) Записать общее уравнение прямой, параллельной прямой 2x + 3y =1 и проходящей
через точку А(2;-1).
2.) Луч света, выйдя из точки А(2;3), отражается от оси OX, и попадает в точку В(5;8). Составить уравнение падающего и отраженного лучей.
3.) Найти координаты центра окружности, описанной около треугольника со сторонами 3x + 4y − 29= 0, 3x − y − 4= 0,x − 2y −13= 0.
Вариант №14
1.) Дана прямая x + 2y −10= 0. Указать: 1) направляющий вектор прямой;
2)угловой коэффициент прямой.
3)отрезки, отсекаемые прямой на осях
координат.
2.) Найти уравнение серединного перпендикуляра к отрезку, соединяющему точки А(-5;-1)иВ(-3;4).
3.) Записать уравнения катетов прямоугольного равнобедренного треугольника, если С(5;-1)-вершинапрямого угла, 2x −3y +5= 0 — уравнение гипотенузы.
Вариант №15
1.) Через точку пересечения прямых x + 2y −1= 0 и 2x + y −4= 0 провести прямую:
проходящую через точку М(-1;3),параллельно оси OY.
2.) Стороны квадрата лежат на прямых 5x −12y −65= 0, 5x −12y + 26= 0. Найти площадь квадрата.
3.) Пусть точка А(3;4)-вершинауглаϕ = 30o прямоугольного треугольника,
x − y +2= 0-уравнениепротиволежащего катета. Найти уравнения двух других сторон треугольника.
Вариант №16
1.) Дана прямая 5x + 4y −3= 0 . Найти 1) направляющий вектор прямой, 2) угловой
коэффициент прямой, 3) отрезки отсекаемые прямой на осях координат.
2.) Даны три вершины треугольника A(−1,3),B(3,−2),C(5,3). Составить уравнения :
1)медианы, проведенной из вершины В,
2)высоты, опущенной из вершины С на сторону АВ,
3)прямой, проходящей через вершину А, параллельно стороне ВС. 3.) Даны две вершины треугольника А(-1,3), B(3,2), уравнения стороны
BC : 2x −3y = 0 и медианыAM :3x + y = 0. Составить уравнение высоты,
опущенной из вершины С на сторону АВ.
|
Вариант №17 |
|
|
1.) |
Найти угол между прямыми 3x − 2y +5= 0,x −5y +8= 0. |
|
2.) |
Найти уравнение прямой, проходящей через точку пересечения прямых |
|
x −3y + 2= 0, 5x + 6y − 4= 0 и параллельной прямой 4x + y −7= 0 . |
|
|
3.) |
Составить уравнения сторон треугольника, зная одну из его вершин А(-1,3)и |
|
уравнения двух высот 3x − 4y +8= 0, 5x + 2y −8= 0. |
Вариант №18
|
1.) |
Найти уравнение прямой, проходящей через точку А(-8,0)под угломϕ = |
π |
к |
|
прямой 3x −2y +5= 0 . |
4 |
||
|
2.) |
Через точку М(2,5) провести прямую так, чтобы ее отрезок, заключенный между |
||
|
осями координат, делился в этой точке пополам. |
|||
|
3.) |
Найти координаты вершин параллелограмма, если известны уравнения двух его |
сторон 2x −3y +1= 0,x + y − 2= 0 и точка пересечения диагоналей М(3,32).
Вариант №19
1.) Составить уравнение прямой, которая проходит через точку М(-3,2)и параллельна прямой 2x + y = 7.
2.) Задан треугольник координатами вершин А(-1,-3),B(4,-5),C(2,1). Вычислить длину высоты, проведенной из вершины В.
3.) Составить уравнения АС и ВС сторон треугольника АВС, если точка А(2,5), а уравнения высоты и биссектрисы, выходящих из вершин В и C соответственно: x − 2y + 7= 0, 4x + y −1= 0.
|
Вариант №20 |
|
|
1.) |
Найти угол между прямыми 2x +3y −5= 0,x −3y −7= 0. |
|
2.) |
Найти угол между прямой 2x −3y +6= 0 и прямой, проходящей через точки |
|
М(4,-5),N(-3,2). |
|
|
3.) |
Даны вершины А(-2,1),B(3,- 4) треугольника АВС и точка пересечения его высот |
|
К(5,-1).Составить уравнения сторон этого треугольника. |
Вариант №21
1.) Дана прямая 3x −5y −7= 0.Составить уравнение прямой проходящей через точку
А(2,-1)параллельно данной прямой.
2.) Даны вершины треугольника А(-10,-13),B(-2,3),C(2,1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
3.) Составить уравнения сторон треугольника, зная его вершину А(-6,3),уравнения высоты 7x +3y −5= 0 и медианы 9x + y −15= 0, проведенных из одной вершины.
Вариант №22
1.) Дана прямая 3x − y + 4= 0. Указать: 1) нормальный вектор прямой;
2.) направляющий вектор прямой;
3) угловой коэффициент прямой.
2.) Найти уравнение прямой, проходящей через начало координат и образующей с прямой y = 2x +3 угол 45o.
3.) Найти внутренние углы треугольника, если даны уравнения его сторон AB 😡 −3y +3= 0,AC 😡 +3y +3= 0, и основаниеД(-1,3)высоты АД.
Вариант №23
1.) Составить каноническое уравнение прямой, проходящей через точку М(7,-2)параллельно биссектрисе координатных углов.
2.) Найти уравнение геометрического места точек, удаленных от прямой 3x − 4y +10= 0 на расстояние, равное 2.
3.) Даны две смежные вершины параллелограмма А(-3,1)и В(2,2) и точка пересечения его диагоналей М(3,0). Составить уравнения высот параллелограмма, проведенных из вершины А.
|
Вариант №24 |
|
|
1.) |
Прямая проходит через точки М(-1,3)и N(2,5). Найти : |
|
1) направляющий вектор прямой; |
|
|
2.) нормальный вектор прямой; |
|
|
3) угловой коэффициент прямой. |
|
|
2.) |
Вычислить угол между прямыми 5y + 4= 0, 3x −3y −3= 0. |
|
3.) |
Даны уравнения двух сторон прямоугольника x −3y + 6= 0, 3x + y −12= 0 и точка |
|
пересечения его диагоналей М(7;2). Составить уравнения двух других сторон |
|
|
прямоугольника. |
Вариант №25
1.) Луч света направлен по прямой y = 3x −6. Дойдя до оси абсцисс, он от нее
отразился. Определить точку встречи луча с осью ОX и уравнение отраженного луча.
2.) Дан треугольник с вершинами A(0;5), B(3;1), C(-6,-3).Найти уравнение медианы СЕ и биссектрисы АД.
3.) В равнобедренном прямоугольном треугольнике даны координаты вершины острого угла А(-1;3)и уравнение противолежащего катета 2x −3y +1= 0.
Составить уравнения двух других сторон треугольника.
Вариант №26
1.) Найти угол между прямыми y = 2x −5,y = −12 x +1.
2.) Составить уравнение прямой, которая проходит через точку пересечения прямых x + y − 2= 0 и 3x + 2y −5= 0 перпендикулярно к прямой 3x + 4y −12= 0.
3.) Найти координаты центра окружности, описанной около треугольника со сторонами 3x + 4y − 29= 0, 3x − y − 4= 0,x − 2y −13= 0.
Вариант №27
1.) Составить каноническое уравнение прямой, проходящей через точку А(2;-1)перпендикулярно к прямойy = −3x +1. Найти отрезки, отсекаемые этой прямой а
осях координат.
2.) Луч света, выйдя из точки А(2;3), отражается от оси OX, и попадает в точку В(5;8). Составить уравнение падающего и отраженного лучей.
3.) Записать уравнения катетов прямоугольного равнобедренного треугольника, если С(5;-1)-вершинапрямого угла, 2x −3y +5= 0 — уравнение гипотенузы.
Вариант №28
1.) Записать общее уравнение прямой, параллельной прямой 2x + 3y =1 и проходящей
через точку А(2;-1).
2.) Найти уравнение серединного перпендикуляра к отрезку, соединяющему точки А(-5;-1)иВ(-3;4).
3.) Пусть точка А(3;4)-вершинауглаϕ = 30o прямоугольного треугольника,
x − y +2= 0-уравнениепротиволежащего катета. Найти уравнения двух других сторон треугольника.
Вариант №29
1.) Дана прямая x + 2y −10= 0. Указать: 1) направляющий вектор прямой;
2)угловой коэффициент прямой.
3)отрезки, отсекаемые прямой на осях координат.
2.) Стороны квадрата лежат на прямых 5x −12y −65= 0, 5x −12y + 26= 0. Найти
площадь квадрата.
3.) Вычислить координаты вершин ромба, если известны уравнения двух его сторон x − 2y +5= 0,x − 2y −5= 0 и одной из диагоналейx +8y −5= 0.
|
Вариант №30 |
|
|
1.) |
Через точку пересечения прямых x + 2y −1= 0 и 2x + y −4= 0 провести прямую: |
|
проходящую через точку М(-1;3),параллельно оси OY. |
|
|
2.) |
Две стороны квадрата лежат на прямых 3x + 4y + 22= 0, 3x + 4y −13= 0. |
|
Вычислить площадь квадрата. |
|
|
3.) |
Провести прямую так, чтобы ее отрезок, заключенный между двумя данными |
|
прямыми: 2x + y −1= 0,x +3y + 2= 0, делился в точкеМ(-1,0)пополам. |
studfiles.net
Контрольная работа «аналитическая геометрия» Контрольные варианты к задаче 1
Даны координаты
вершин треугольника АВС. Требуется:
1) вычислить
длину стороны ВС;
2) составить
уравнение линии ВС;
3) составить
уравнение высоты, проведенной из вершины
А;
4) вычислить
длину высоты, проведенной из вершины
А;
5) найти точку
пересечения медиан;
6) вычислить
внутренний угол при вершине В;
7) найти координаты
точки М, расположенной симметрично
точке А относительно прямой ВС.
|
1. |
. |
2. |
. |
|
3. |
. |
4. |
. |
|
5. |
. |
6. |
. |
|
7. |
. |
8. |
. |
|
9. |
. |
10. |
. |
|
11. |
. |
12. |
. |
|
13. |
. |
14. |
. |
|
15. |
. |
16. |
. |
|
17. |
. |
18. |
. |
|
19. |
. |
20. |
. |
|
21. |
. |
22. |
. |
|
23. |
. |
24. |
. |
|
25. |
. |
26. |
. |
|
27. |
. |
28. |
. |
|
29. |
. |
30. |
. |
Контрольные варианты к задаче 2
1. Вершина
квадрата
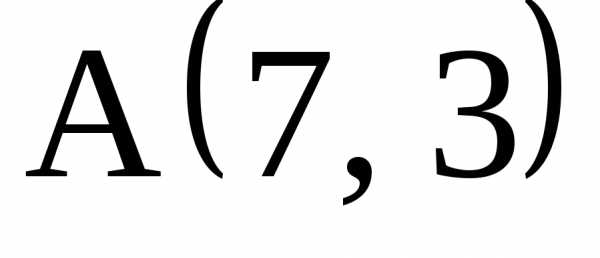
сторона СD
лежит на прямой, отсекающей на осях
координат отрезки
.
Написать уравнение стороны АД (Квадрат
АВСD).
2. В треугольнике
АВС даны уравнения: высоты
,
высоты
и стороны.
Составить уравнение третьей высоты.
3. Найти точку,
симметричную точке
относительно прямой.
4. Составить
уравнение прямой, проходящей через
точку пересечения прямых
и
и образующей угол в
прямой.
5. Через точку
пересечения прямых
провести прямую перпендикулярно прямой.
6. В треугольнике
АВС даны уравнения: стороны АВ
и высот.
Составить уравнения двух других сторон
треугольника.
7. Вычислить
координаты вершин ромба, если известны
уравнения двух его сторон ()
и уравнение одной из его диагоналей.
8. Из точки
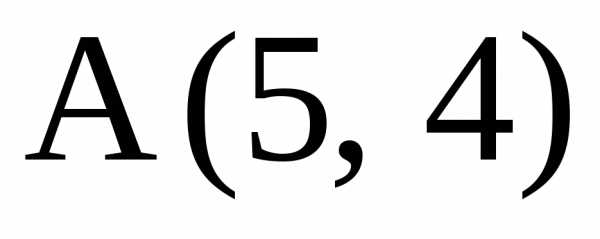
уравнения падающего и отраженного
лучей.
9. Под каким
углом к оси Ох наклонена прямая, проходящая
через точки
.
10. В квадрате
АВСD
даны вершина
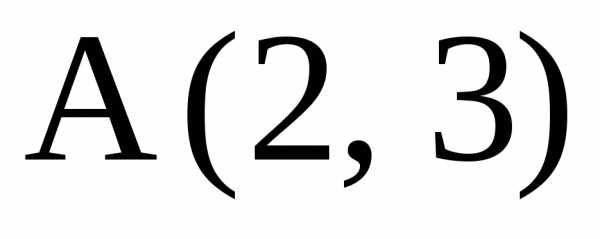

точка пересечения диагоналей. Найти
уравнения сторон квадрата, не проходящих
через верши-
ну А.
11. Даны точки
.
Отрезок АС разделен точкойD
в отношении
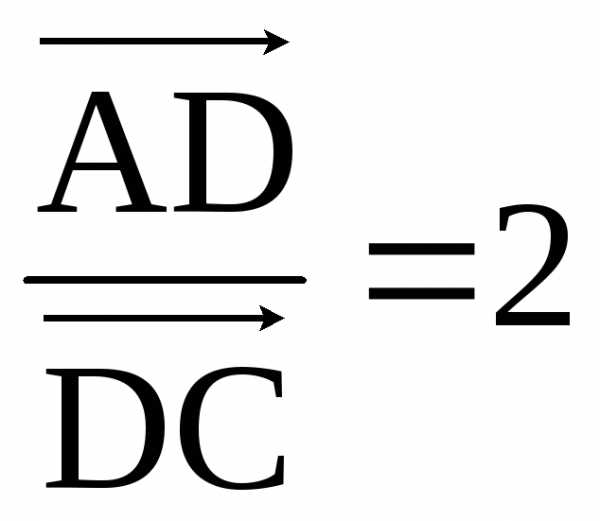
Найти расстояние от точки А до прямой
ВD.
12. Отрезок
прямой
,
заключенный между осями координат,
является диагональю квадрата. Найти
уравнение одной (любой) стороны квадрата.
13. Через точку
пересечения прямых
провести прямую перпендикулярно прямой.
14. Даны уравнения
двух сторон параллелограмма:
и точка пересечения диагоналей
Составить уравнения двух других сторон
параллелограмма.
15. Составить
уравнения прямых, проходящих через
точку
и составляющих угол
16. Даны уравнения
двух сторон параллелограмма
-и точка пересечения
его диагоналей
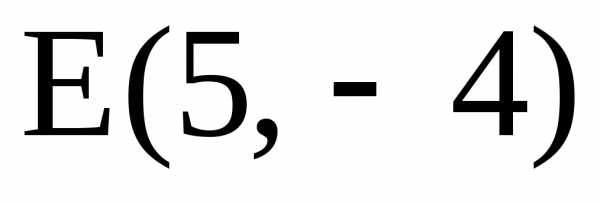
Составить уравнения
двух других его
сторон.
17. Даны середины
противоположных сторон квадрата
.
Написать уравнения двух сторон квадрата,
на которых лежат точки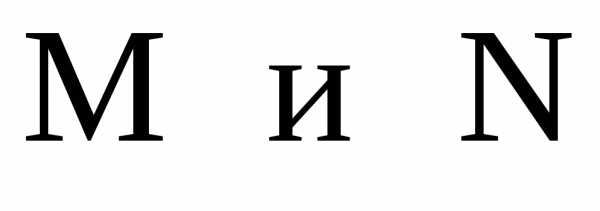
18. Провести
прямую так, чтобы точка
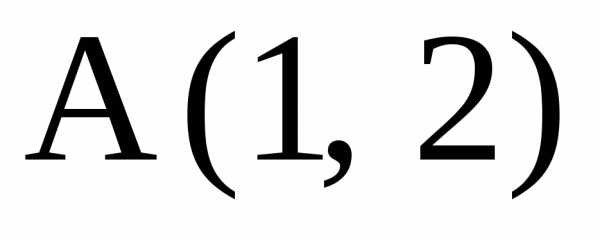
между осями координат. Составить
уравнение этой прямой.
19. Даны две
точки:
.
Через середину отрезка АВ провести
прямую, отсекающую от оси Ох отрезок,
вдвое больший, чем отрезок на оси Оу.
20. В треугольнике
АВС даны вершины:
.
Определить: а) угол между стороной АВ
и медианой стороны ВС; б) длину высоты,
опущенной из вершины С.
21. Составить
уравнения катетов прямоугольного
равнобедренного треугольни-
ка, зная уравнение
гипотенузы
и вершину прямого угла.
22. Составить
уравнение прямой, проходящей через
точку
и отсекающей от координатного угла
треугольник площадью 8 дм2.
23. В треугольнике
АВС даны вершины:
.
Найти точку, симметричную точке В
относительно стороны АС.
24. В треугольнике
АВС даны вершины:
.
Найти угол между медианой АМ и высотой
ВН.
25. Даны точки
.
На отрезке ОА ( О – начало координат),
построить параллелограмм ОАСД, диагонали
которого пересекаются в точке В. Написать
уравнения сторон и диагоналей
параллелограмма.
26. Под каким
углом к оси Ох наклонена прямая, проходящая
через точки
?
27.Составить
уравнение прямой, проходящей через
точку пересечения прямых
и образующую с осью Ох угол, вдвое больший
угла, образованного с той же осью прямой.
28. Найти точку,
симметричную точке
относительно прямой.
29. Прямая

Найти точку, симметричную точке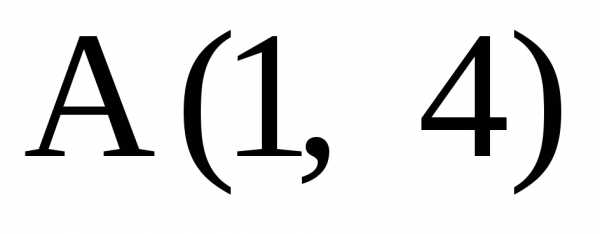
30. Даны уравнения
двух сторон параллелограмма:
-и одна из его
вершин
.
Найти точку пересечения его диагоналей.
studfiles.net
4.5. Варианты контрольных заданий для контрольной работы № 2 Элементы векторной алгебры и аналитической геометрии
1.
Параллелограмм построен на векторах
и.
Найти
: 1) длины диагоналей параллелограмма;
2) косинус угла между диагоналями; 3)
;
4) площадь параллелограмма.
2.
Даны координаты вершин пирамиды
.
1)
Найти модуль вектора
2)
Найти площадь грани
3)
Найти длину высоты, опущенной из вершины
4)
Найти косинус угла между векторами
и
5)
Записать уравнение плоскости
6)
Записать
уравнение высоты, опущенной из вершины
на грань
3.
В соответствии с вариантом выполнить
следующие задания.
-
Найти
точку пересечения медиан треугольника,
зная координаты его вершин: -
Даны
уравнения двух смежных сторон
параллелограмма
и точка пересечения его диагоналей.
Составить уравнения двух других сторон
параллелограмма. -
Даны
вершины треугольника
и точка пересечения его высот.
Составить уравнения сторон треугольника. -
Даны
вершины треугольника:
Найти длины его высот. -
Составить
уравнения сторон квадрата, если известны
одна из вершин
и точка пересечения диагоналей. -
Даны
уравнения сторон прямоугольника
и
одна из его вершин
.
Составить уравнения двух других сторон
этого прямоугольника. -
Даны
уравнения сторон параллелограмма
и
уравнение одной из его диагоналей
Найти координаты вершин этого
параллелограмма.
-
Вычислить
координаты вершин ромба, если известны
уравнения двух других его сторон
и уравнение одной из его диагоналей -
Составить
уравнения сторон треугольника, если
заданы две его вершины
и
точка пересечения медиан -
Даны
вершины треугольника:
Составить уравнения его высот. -
Даны
две смежные вершины квадрата
Составить уравнения его сторон. -
Составить
уравнения сторон и высот треугольника
с вершинами в точках: -
Даны
две стороны прямоугольника
и уравнение его диагонали.
Составить уравнения двух других сторон. -
Составить
уравнения сторон и высот треугольника
с вершинами в точках: -
Три
последовательные вершины параллелограмма
имеют координаты:
Составить уравнения диагоналей этого
параллелограмма. -
Составить
уравнения сторон и найти внутренние
углы треугольника с вершинами в точках: -
Дан
треугольник с вершинами в точках:
Составить уравнения его высот и медиан. -
Даны
вершины треугольника
и точка пересечения его медианСоставить уравнения сторон этого
треугольника. -
Вычислить
координаты вершин ромба, если известны
уравнения его двух сторон
и
одна из его диагоналей. -
Найти
точку пересечения высот треугольника
с вершинами в точках:
-
Привести
уравнение кривой второго порядка
к каноническому виду. Определить вид
кривой и построить ее график.
-
В
соответствии с вариантом решить задачу.
-
Составить
уравнение плоскости, проходящей через
точку
и отсекающей равные отрезки на осях
координат.,
параллельно
плоскости
-
Проверить,
лежит ли прямая -
в
плоскости -
Составить
уравнения плоскости, проходящей через
прямую -
параллельно
прямой -
При
каком значении А плоскость
,
будет параллельна прямой -
Составить
уравнения плоскости, которая проходит
через точку М(3;-2;-7) параллельно плоскости
-
Найти
точку пересечения прямой и плоскости
и -
Из
точки М (2;0;-1) опустить перпендикуляр
на плоскость 2x+3y –z+5=0. -
Привести
к каноническому виду прямую -
Составить
уравнения плоскости, проходящей через
параллельно прямым
и -
Найти
уравнение прямой перпендикулярной к
плоскости
проходящей
через точку М(1;-1;2). -
Найти
угол между прямой
и плоскостью. -
Составить
уравнения плоскости, проходящей через -
и
прямую
. -
Найти
уравнение плоскости, проходящей через
точку
М(1;-2;3)
параллельно прямым
и
-
Найти
точку пересечения прямой
и
плоскости -
Составить
канонические уравнения прямой,
проходящей через точку -
,
параллельно прямой -
Найти
точку Q, симметричную точке Р(1;3:-4)
относительно плоскости -
Найти
проекцию точки Р(5;2;1) на плоскость -
Составит
уравнения плоскости, проходящей через
точку
параллельно плоскости -
Составить
канонические и параметрические
уравнения прямой, проходящей через
точку
перпендикулярно плоскости -
Написать
параметрическое уравнения прямой
проходящей через точку А(5;4;1) параллельно
оси ОХ.
studfiles.net
UCHEES.RU — помощь студентам и школьникам
В 6:07 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Диагонали ромба лежат на координатных осях. Найдите координаты вершин ромба, если середина одной из его сторон имеет координаты (4; -3)
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Диагонали ромба лежат на координатных осях. Найдите координаты вершин ромба, если середина одной из его сторон имеет координаты (4; -3)
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Воронцова Анисья Игоревна — автор студенческих работ, заработанная сумма за прошлый месяц 77 800 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 — 2023 — UCHEES.RU

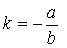

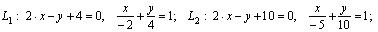
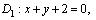
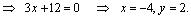

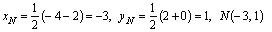
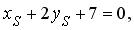
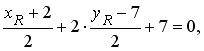
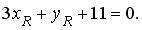
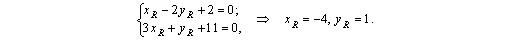
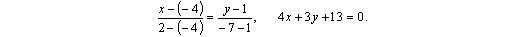

 ;
; ;
;
 ;
; .
.
 .
.
 найдем по точке и перпендикулярному
найдем по точке и перпендикулярному .
. можно найти разными способами (Рис.
можно найти разными способами (Рис.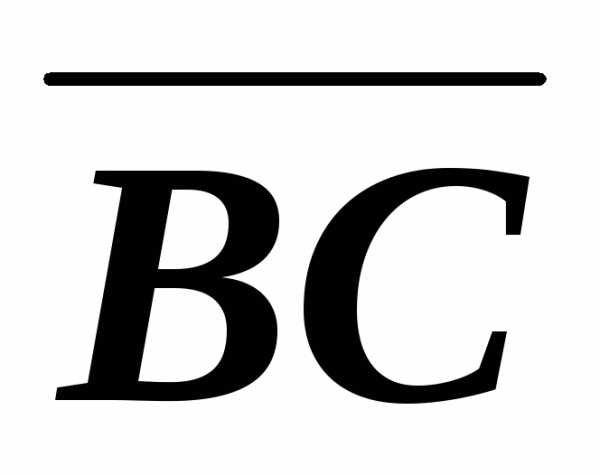
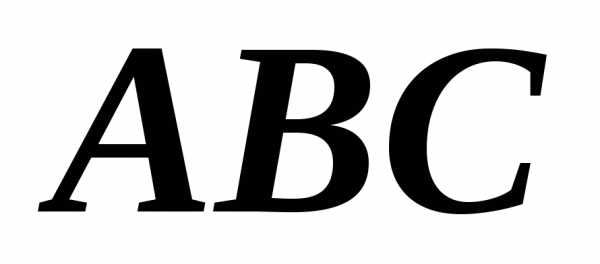 .
.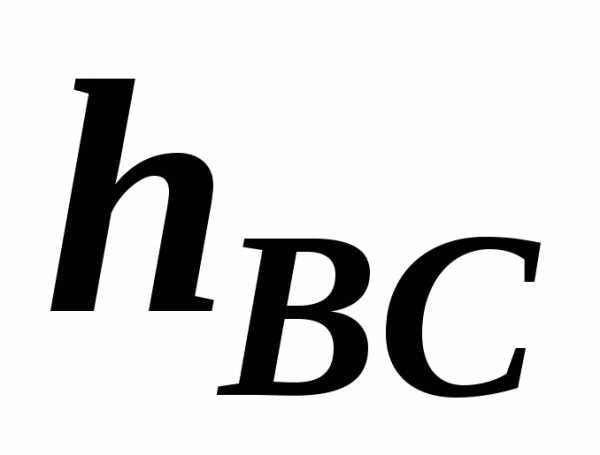
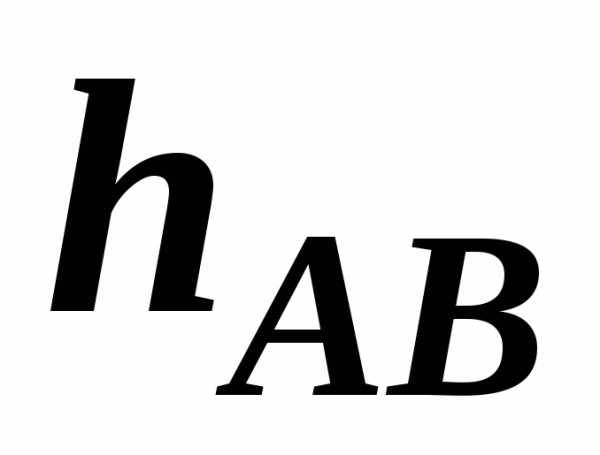
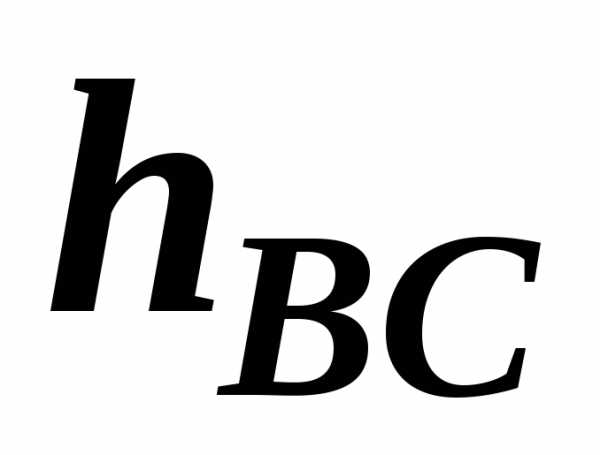

 .
.
 .Ответ: .
.Ответ: .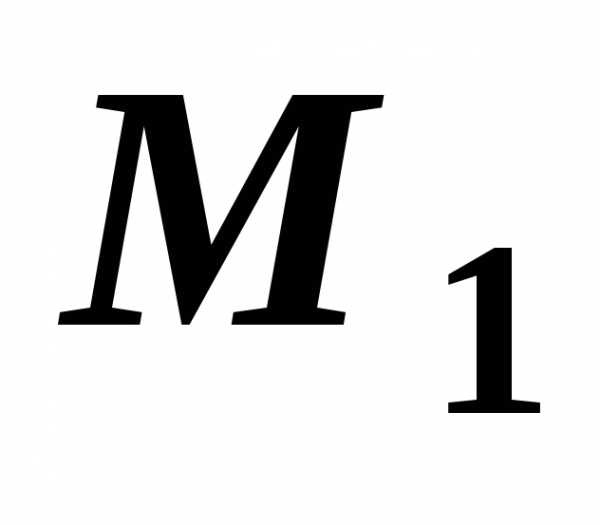 ,
, и
и являются
являются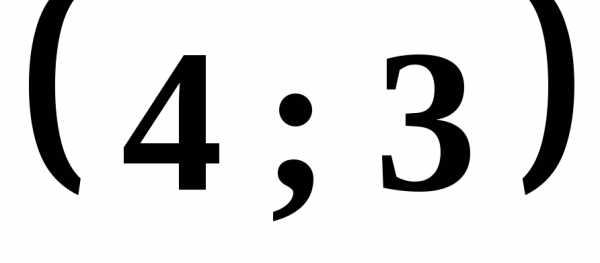
 ,
, .Ответ:
.Ответ: ,
, .
.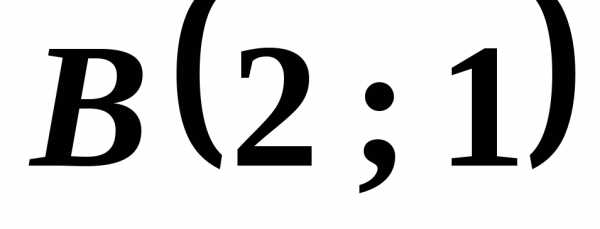 ,
, и
и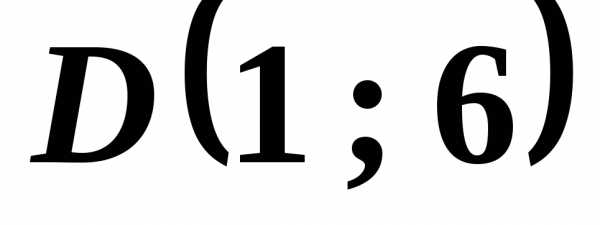 –
–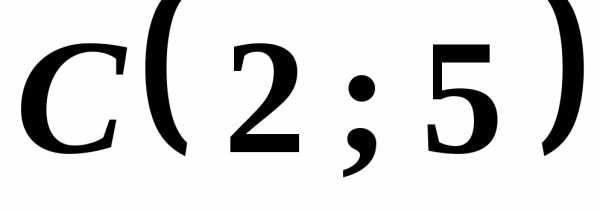 ,.
,. на
на с прямой, проходящей через вершину
с прямой, проходящей через вершину .
.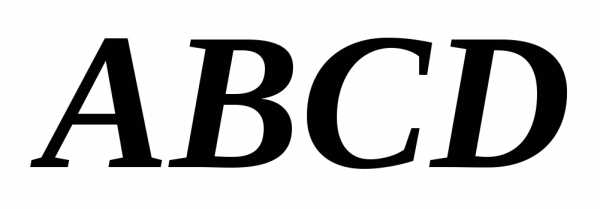 :.
:. этой трапеции.
этой трапеции.
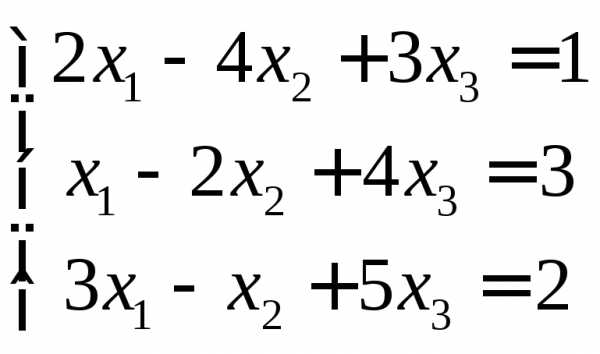
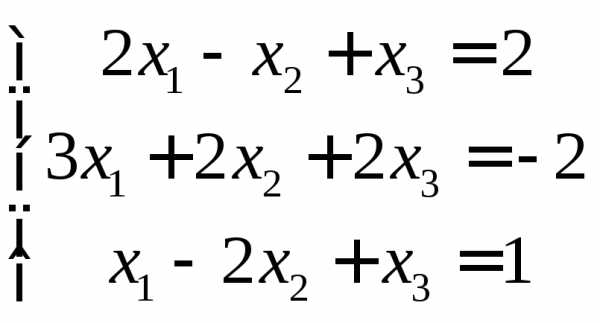
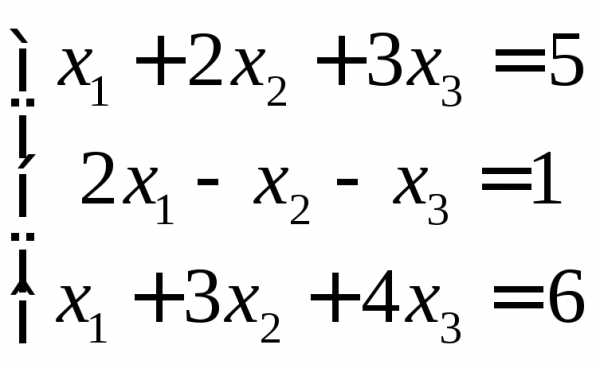
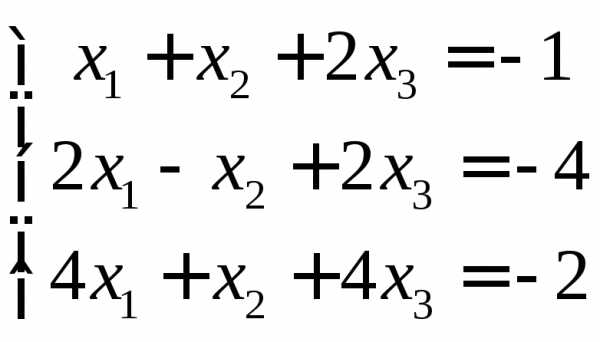
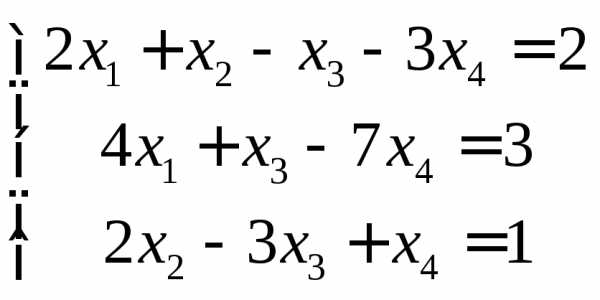
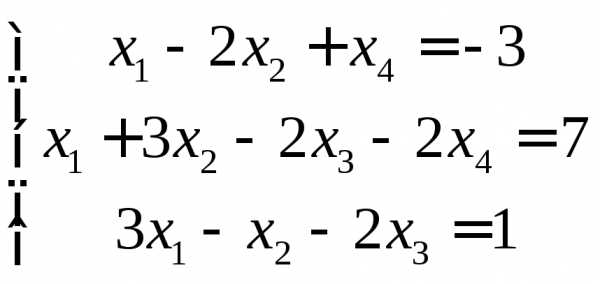

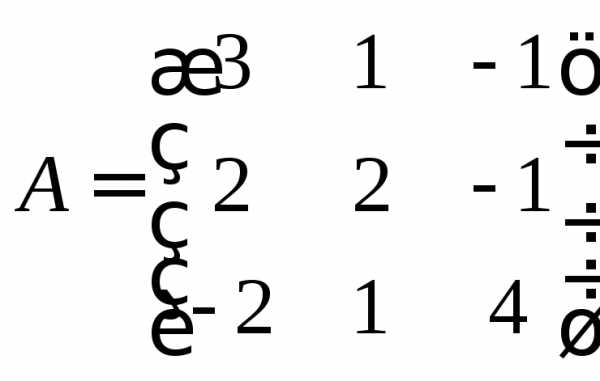
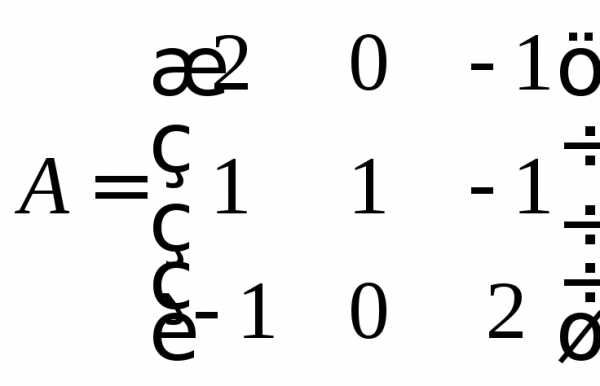
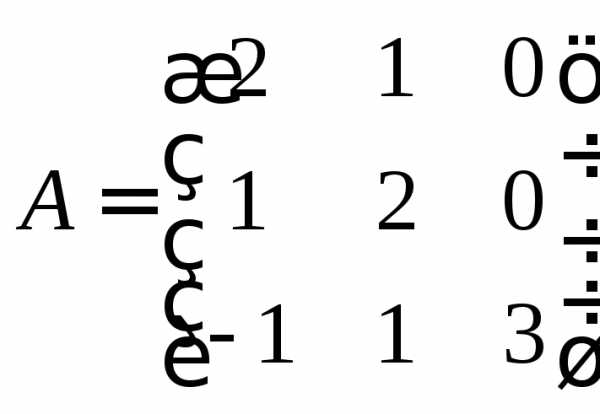
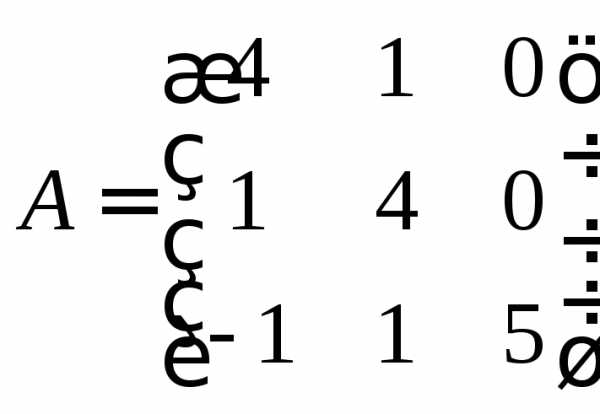
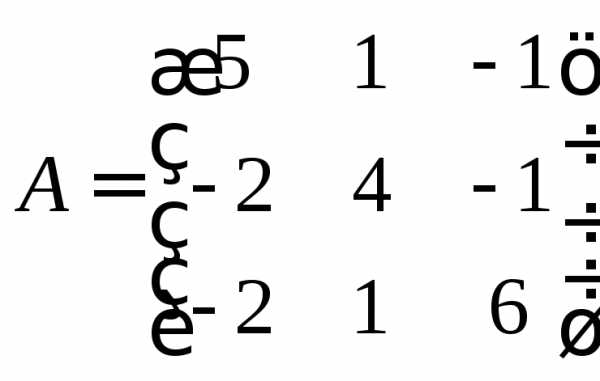
 и уравнения двух медиани
и уравнения двух медиани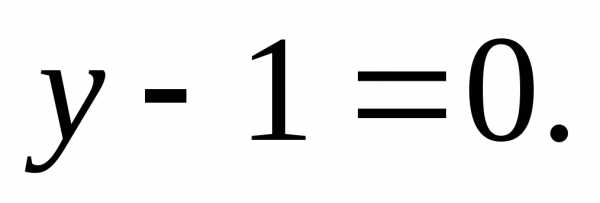 Сделать
Сделать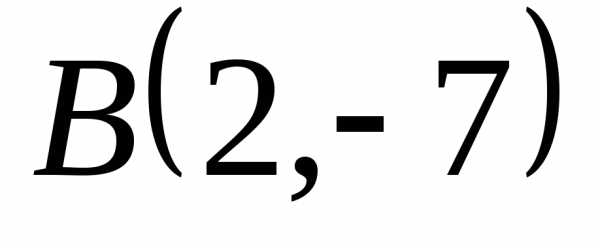 ,
,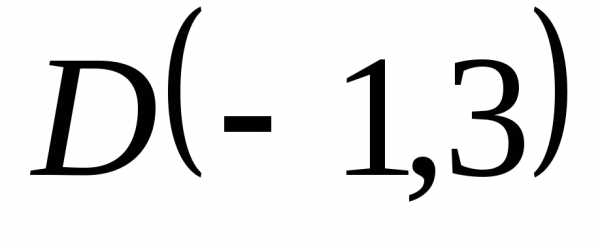 высотыAD.
высотыAD.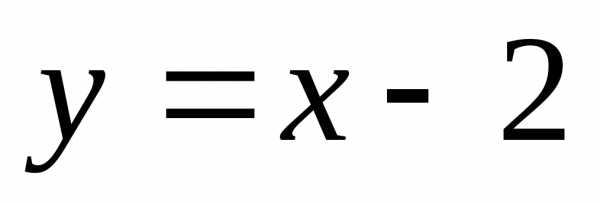 и.
и.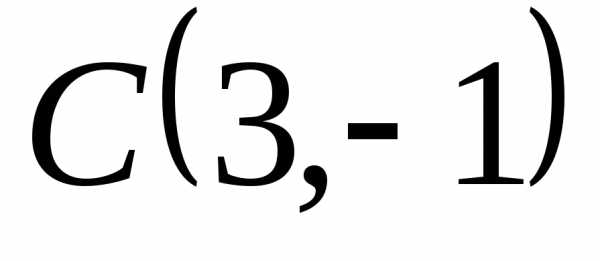 и уравнение гипотенузыСделать
и уравнение гипотенузыСделать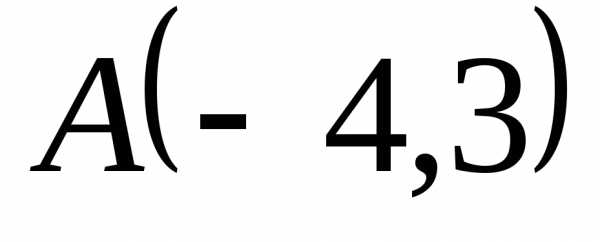 и
и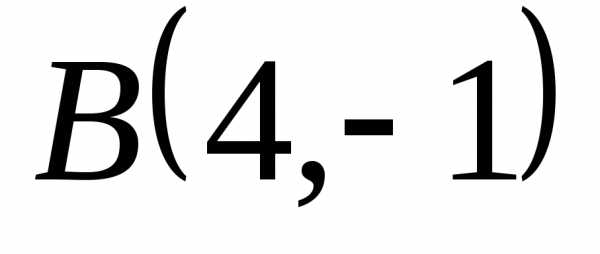 и точка пересечения высот
и точка пересечения высот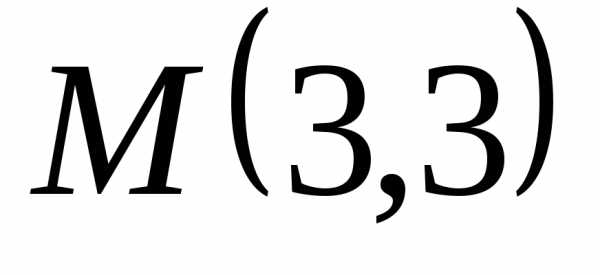 .
.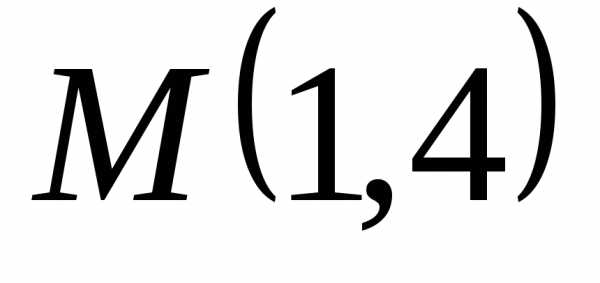 .
.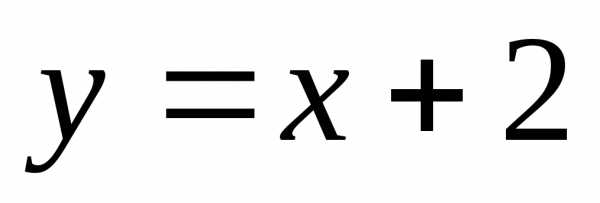 .
.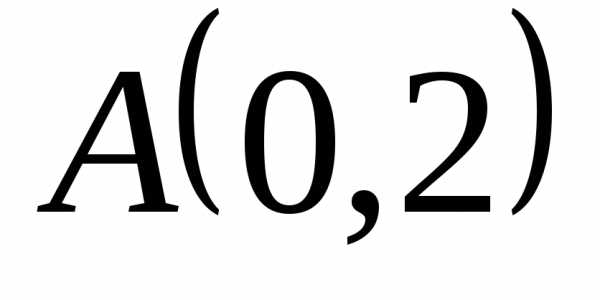 ,
, ,
, и от оси
и от оси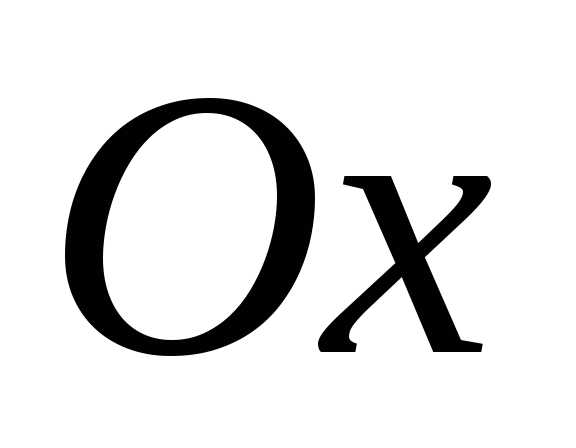 .
. и
и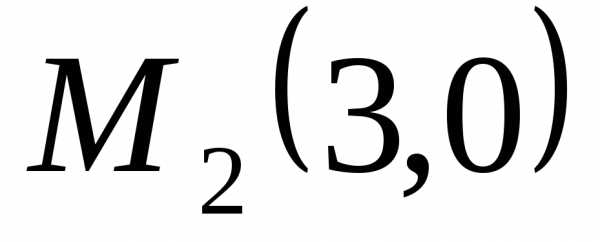 равна 50. Сделать чертеж.
равна 50. Сделать чертеж.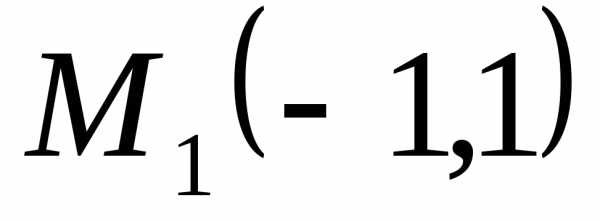 вдвое меньше расстояния до точки.
вдвое меньше расстояния до точки. равен 4. Сделать чертеж.
равен 4. Сделать чертеж.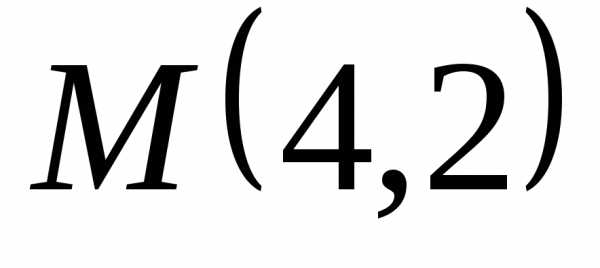 и от оси
и от оси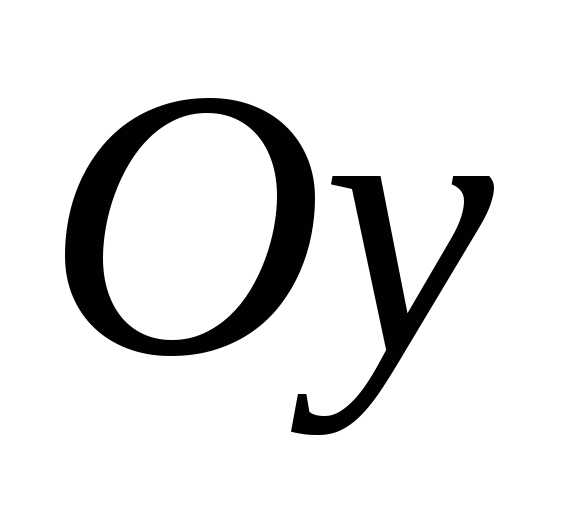 .
.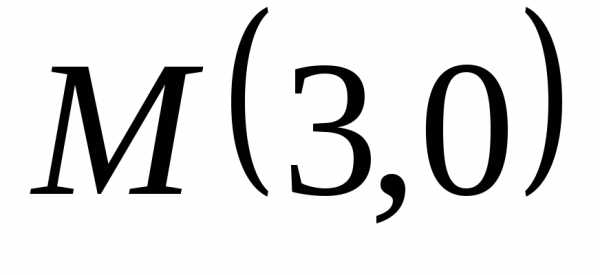 вдвое дальше, чем от прямой
вдвое дальше, чем от прямой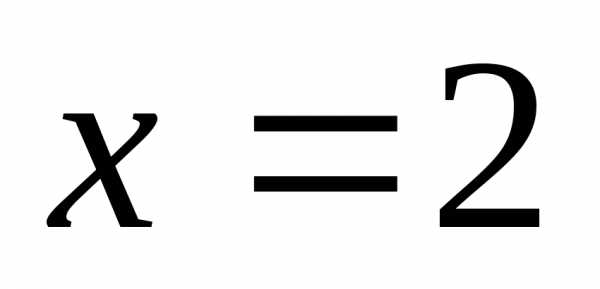 .
.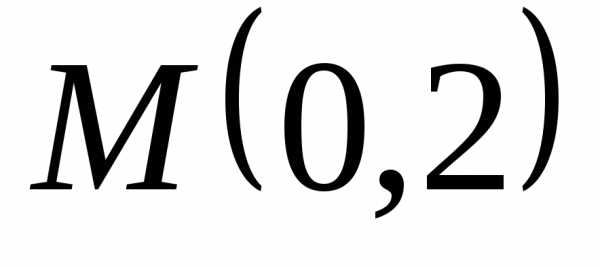 вдвое меньше расстояния от прямой
вдвое меньше расстояния от прямой .
.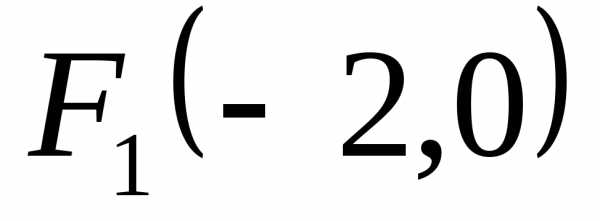 и
и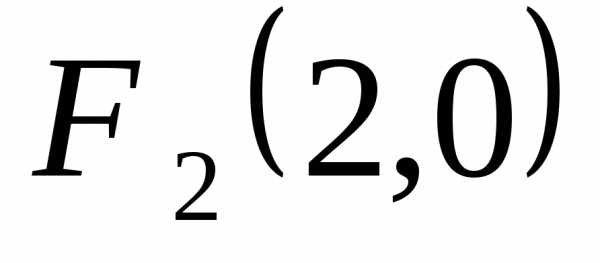 равна 2
равна 2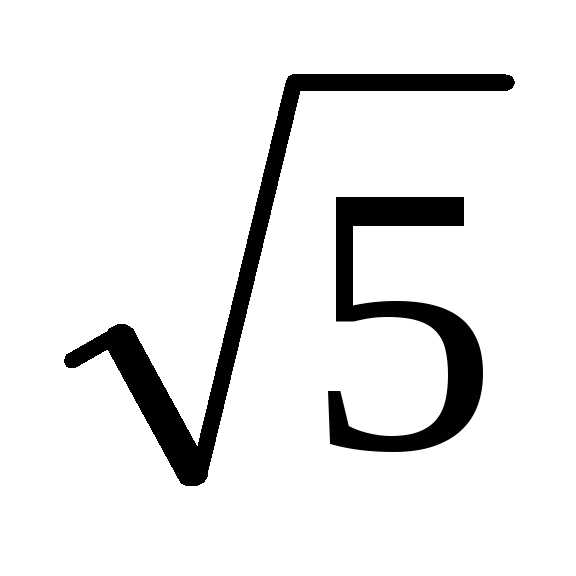 .
.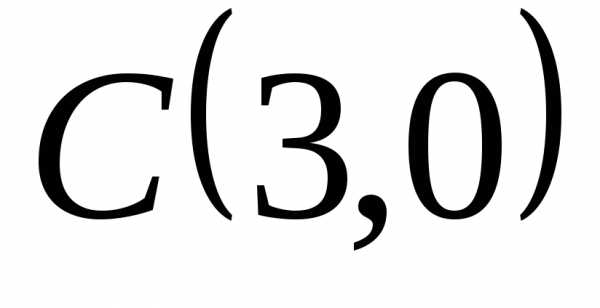 равна 27. Сделать чертеж.
равна 27. Сделать чертеж.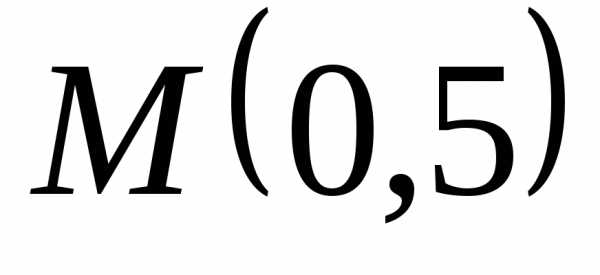 относятся как 3:2. Сделать чертеж.
относятся как 3:2. Сделать чертеж.