1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
import numpy as np from scipy.spatial.distance import pdist points=np.array([[float(input(f'{i}{j}=')) for i in 'xy']for j in '₁₂₃']) #points=np.array([[2.0, 1.0], [5.0, -1.0], [4.0, 4.0]]) edges_dist=pdist(points)[::-1] # the last point opposite the long side of the triangle: ordered_points=points[np.argsort(edges_dist), :] # homogeneous coordinates: ordered_points_homogeneous=np.hstack((ordered_points, np.ones((3,1)))) # translate matrix T=np.array([[1,0,0], [0,1,0],[-ordered_points[0,0],-ordered_points[0,1],1]]) # rotate angle angle=np.arctan2((ordered_points_homogeneous@T)[1,1], (ordered_points_homogeneous@T)[1,0]) # rotate matrix: R=np.array([[np.cos(angle),-np.sin(angle),0], [np.sin(angle),np.cos(angle),0],[0,0,1]]) # mirror matrix M=np.array([[1,0,0], [0,-1,0],[0,0,1]]) # all transform matrix: A=T@R@M@np.linalg.inv(R)@np.linalg.inv(T) # fourth vertex of the square: pos=(ordered_points_homogeneous[2,:]@A)[:-1] print(f'x₄={pos[0]:.2f}, y₄={pos[1]:.2f}') |
I was given this problem:
Without drawing a graph and given the following 3 vertices, find the coordinates of the last vertex of the square:
$(3,2)$$(0,5)$$(-3,2)$
So first, I found the length of the sides and the diagonal of the square, which are $sqrt{18}$ and $6$ respectively. By graphing, I know the solution is $(0, -1)$. Then, I assume that since the length between $(3,2)$ and $(-3,2)$ is the diagonal, then the distance between $(0,5)$ and the remaining vertex must be the diagonal too. And since the length of the side is 6, then the distance between the vertex and either $(3,2)$ or $(-3,2)$ must be 6. So:
$$sqrt{(x-3)^2+(y-2)^2}=sqrt{18}$$
$$sqrt{(x-0)^2+(y-5)^2}=6$$
Which gives (after a bit of cleaning up):
$$x^2+y^2-10y=11$$
$$x^2-6x+y^2-4y=5$$
Then, replacing the second expression into the first one:
$$x^2-6x+y^2-4y=5 Rightarrow x^2=5+6x-y^2+4y$$
$$require{cancel}5+6x-cancel{y^2}+4y+cancel{y^2}-10y=11$$
$$5+6x+4y-10y=11$$
$$6x-6y+6$$
$$x-y=1$$
$$x=1+y$$
Up to this point, I know I’m not entirely wrong because the expression is true for the actual coordinates of the vertex, because $0=1+(-1)$ is true. But I wouldn’t know how to proceed if I hadn’t known the answer beforehand. I need to find both $x$ and $y$, is there a linear equation I’m missing to find the exact coordinates of the last vertex? Is my process okay or is there a simpler way to do it?
@victor1234
IT: Компьютерное зрение, linux, с++
Как найти четвертую вершину квадрата, видимого под углом, зная первые три и длину стороны?
Условно есть квадрат, лежащий на горизонтальной поверхности. Камера видит его под углом. С нее я получаю три координаты вершины. Как мне вычислить четвертую?
-
Вопрос заданболее трёх лет назад
-
3198 просмотров
В качестве математической модели для камеры обычно берут центральную проекцию. Я почти уверен, что центральная проекция некоторой плоскости есть аффинное преобразование. Для квадрата ABCD верно векторное(!) равенство AC = AB + AD. При Аффинном преобразовании это равенство сохранится.
Пригласить эксперта
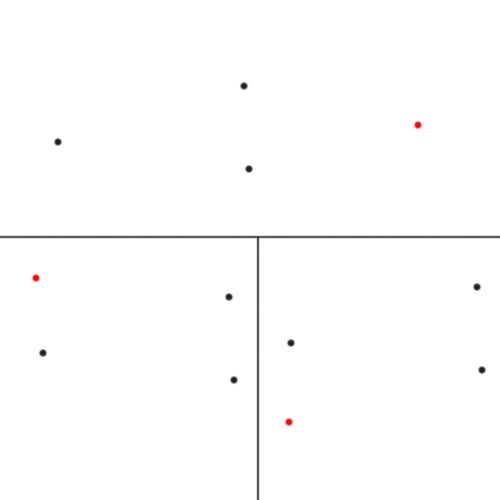
Однозначное решение задачи без знания взаимного расположения камеры и плоскости принципиально невозможно. Проиллюстрирую.
Черными метками — известные нам точки, красной — валидные варианты расположения четвертого угла при разных положениях камеры.
-
Показать ещё
Загружается…
25 мая 2023, в 17:40
1 руб./за проект
25 мая 2023, в 17:10
1500 руб./в час
25 мая 2023, в 17:00
20000 руб./за проект
Минуточку внимания

32. Даны три вершины квадрата А(2; 1), B(5; – 2), С(5; 4). Найдите координаты четвертой вершины квадрата.
Задача 31255 Известна точка пересечения диагоналей.
Условие
Известна точка пересечения диагоналей квадрата K(2,5; 4,5)
и уравнение одной из его сторон
x -4y + 24 = 0
. Найти
координаты вершин квадрата и составить уравнения его
диагоналей.
Все решения
Уравнение стороны запишем в виде
y=(1/4)x+6
k=1/4
tg α =1/4
Тогда
уравнение диагонали:
y=k_(1)x+b
tg β =k_(1)
tg( β — α )=(tg β -tg α )/(1+tg β *tg α )
y=(5/3)x+b — уравнение диагонали
Подставим координаты точки К
Диагонали взаимно перпендикулярны.
Значит уравнение второй диагонали
y=(-3/5)x+b
Подставим координаты точки К
4,5=(-3/5)*2,5+b
b=6
Координаты одной вершины получим как координаты точки пересечения стороны х-4у+24=0 и диагонали у=(5/3)х+(1/3)
<х-4у+24=0
<у=(5/3)х+(1/3)
x=4
y=7
Координаты второй вершины получим как координаты точки пересечения стороны х-4у+24=0 и диагонали у=(-3/5)х+6
<х-4у+24=0
<у=(-3/5)х+6
x=0
y=6
Координаты двух других точек можно найти из симметрии.
Уравнение квадрата в декартовой системе координат.
Проанализируем расположение квадрата на координатной плоскости.
В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:
где точка О`(a;b) – точка пересечения диагоналей квадрата;
d – длина диагонали квадрата.
В частном случае, когда точка О(0;0) — начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:
где d– длина диагонали квадрата.
Раздел 1
Задача. Пусть точка А(1; 3) — вершина квадрата ABCD, а его диагональ BD лежит на прямой х + 2у — 12 = 0. Найти:
а) координаты вершин В, С и D;
b) уравнения сторон АВ, ВС, CD и AD.
Указание. Из школьного курса геометрии известны следующие свойства диагоналей квадрата, которые будут использованы при решении этой задачи.
Диагонали квадрата: 1) взаимно перпендикулярны; 2) делятся точкой своего пересечения — центром квадрата — пополам; 3) равны.
Решение: 1. Найдем уравнение прямой, на которой лежит АС — вторая диагональ квадрата. Вспомним, что уравнение любой невертикальной прямой может быть приведено к виду у = kx + b, где параметр k — угловой коэффициент этой прямой.
В силу свойства диагоналей квадрата угловые коэффициенты =-0,5 и kBD прямых АС и BD связаны соотношением
Найдем угловой коэффициент kBD. Для этого выразим у через х из данного уравнения прямой BD: 2у = — х + 12, откуда у =-0,5 х + 6. Итак, kBD =-0,5. Поэтому из соотношения (1) получим, что kAC=2.
Теперь уже легко найти уравнение прямой АС. Нам известны координаты ее точки А и угловой коэффициент kAC. Используем уравнением прямой, проходящей через данную точку в данном направлении:
Подставим в это уравнение числовые данные нашей задачи: xA = 1, уА = 3, kAC=2. Получим у — 3 = 2(х — 1) или (после упрощений)
AC: у = 2х + 1.
2. С помощью свойства 2) диагоналей квадрата найдем координаты центра Е квадрата — точки пересечения его диагоналей.
Поскольку точка Е лежит на диагонали АС, ее координаты удовлетворяют уравнению прямой АС; аналогично рассуждая, получим, что координаты точки Е должны одновременно удовлетворять и уравнению прямой BD. Таким образом, координаты точки Е должны удовлетворять системе из уравнений прямых АС и BD
(первое — уравнение прямой АС, второе — прямой BD).
Далее, вычитая второе уравнение из первого, получим: 0=2,5x-5. Значит х = 2. Подставим найденное значение х в любое из уравнений системы, например, в первое. Найдем, что у = 5.
Итак, мы нашли координаты точки Е, центра квадрата: хЕ = 2, уЕ = 5, т.е. Е(2; 5).
3. Найдем длину отрезка АЕ — половину диагонали квадрата, а затем воспользуемся тем, что и остальные вершины квадрата находятся от его центра E на таком же расстоянии (свойства 2) и 3) диагоналей), т.е. что все вершины квадрата лежат на окружности радиуса АЕ с центром в точке Е
Подставив в правую часть этой формулы числовые значения координат точек А и Е, получим, что
Уравнение окружности радиуса АЕ с центром в точке Е записывается в виде
Подставив в него числовые значения радиуса АЕ и координат центра Е, получим уравнение окружности, проходящей через все вершины квадрата:
Теперь с помощью простого рассуждения находим по очереди координаты всех вершин квадрата.
Точки А и С лежат на пересечении найденной окружности и прямой АС, это общие точки указанных окружности и прямой. Значит, координаты этих точек — решения системы уравнений окружности и прямой:
Координаты вершины А мы знаем, поэтому будем искать вершину С.
Подставим во второе уравнение системы вместо у его выражение 2х + 1 из первого уравнения. Получим:
(х — 2) 2 + (2х + 1 — 5) 2 = 5,
откуда (х — 2) 2 + (2х — 4) 2 = 5, поэтому (х — 2) 2 + 4(х — 2) 2 = 5, т.е. 5(х — 2) 2 = 5, значит (х — 2) 2 = 1. Если квадрат числа равен 1, это число равно либо 1, либо (-1). Поэтому х — 2 = 1 и тогда х = 3, либо х — 2 = -1 и тогда х = 1.
Во втором случае мы получили известную нам абсциссу вершины А (а из первого уравнения системы получим ординату этой вершины), а первый случай дает нам абсциссу вершины С: хС = 3. Тогда из первого уравнения системы найдем ординату вершины С: уС = 2×3 + 1 = 7. Итак, найдена вершина С(3; 7).
Аналогично, для нахождения координат вершин В и D надо решить систему, состоящую из уравнений прямой BD и той же окружности:
Выразим из первого уравнения х через у: х = 12 — 2у.и подставим полученное выражение во второе уравнение системы. Получим (аналогично решению предыдущей системы) 4(у — 5) 2 + (у — 5) 2 = 5, откуда либо у — 5 = 1 и тогда у = 6, либо у — 5 = -1 и тогда у = 4.
При у = 6 первое уравнение системы дает х = 12 — 2у = 12 — 12 = 0, а при у= 4 аналогично получаем, что х = 4.
Итак, получены два решения системы, пары (0; 6) и (4; 4). Одно из этих решений — координаты точки В, а второе — точки D. Поскольку обе эти вершины совершенно равноправны, мы можем любую из них обозначить буквой В, тогда вторая будет вершиной D. Вся разница в том, идут ли вершины А, В, С и D в порядке обхода контура квадрата по или против часовой стрелки, что для решения нашей задачи безразлично; просто надо выбрать одно из этих направлений произвольно.
Мы будем считать, что вершины квадрата таковы: B(0; 6); D(4; 4).
4. Нам осталось найти уравнения сторон квадрата. Для этого вспомним уравнение прямой, проходящей через точки М(хМ; уМ) и N(xN; yN):
(2)
и подставим в него координаты соответствующих вершин квадрата.
Уравнение прямой АВ получим, если в формуле (2) вместо точек М и N возьмем точки А и В:
.
Подставляя в это уравнение координаты вершин А(1; 3) и В(0; 6), находим:
или y-3=-3(x-1), откуда y=-3x+6.
Аналогично получаем уравнения других сторон. Теперь можно сделать чертеж.
Ответ: а) В(0; 6); С(3; 7); D(4; 4);
BC:
DA:
Замечание. Если иначе выбрать точки B и D (cм. п.3 решения), в ответе надо поменять местами: в п. а) — координаты точек В и D; в п. b) — уравнения прямых АВ и CD, а также уравнения прямых ВС и CD.
Дата добавления: 2014-12-02 ; просмотров: 1393 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://www.calc.ru/Uravneniye-Kvadrata-V-Dekartovoy-Sisteme-Koordinat.html
http://helpiks.org/1-18451.html